船舶横摇运动中力矩分析
船舶运动的六个自由度

船舶运动的六个自由度船舶是一种水上交通工具,它可以在水上自由行驶。
船舶运动的六个自由度是指在三维空间中,船舶可以进行六种运动,这些运动包括:横摇、纵摇、艏摇、横荡、纵荡和偏移。
下面将对这六个自由度进行详细的介绍。
一、横摇横摇是指船体绕纵轴旋转的运动。
当外部力矩作用于船体时,会引起船体发生横摇。
例如,在海浪中行驶时,海浪的冲击力会使得船体产生横向振动,从而引起横摇。
二、纵摇纵摇是指船体绕横轴旋转的运动。
当外部力矩作用于船体时,会引起船体发生纵摇。
例如,在大浪中行驶时,浪头和浪谷的冲击力会使得船体产生前后振动,从而引起纵摇。
三、艏摇艏摇是指船首向左或向右侧倾斜的运动。
当外部力矩作用于艏部时,会引起艏部发生摇晃,从而引起艏摇。
例如,在强风中行驶时,风力会使得船首向左或向右倾斜,从而引起艏摇。
四、横荡横荡是指船体在水平方向上的移动。
当外部力矩作用于船体时,会引起船体发生横向位移,从而引起横荡。
例如,在强浪中行驶时,海浪的冲击力会使得船体产生侧向位移,从而引起横荡。
五、纵荡纵荡是指船体在垂直方向上的移动。
当外部力矩作用于船体时,会引起船体发生垂直位移,从而引起纵荡。
例如,在大浪中行驶时,浪头和浪谷的冲击力会使得船体产生上下位移,从而引起纵摇。
六、偏移偏移是指船体在水平面内的旋转运动。
当外部力矩作用于船体时,会使得船体绕一个轴线旋转,并且这个轴线与纵轴和横轴都不重合。
这种运动称为偏移。
例如,在强风中行驶时,风力会使得船体绕一个轴线旋转,从而引起偏移。
总结:船舶运动的六个自由度包括横摇、纵摇、艏摇、横荡、纵荡和偏移。
这些自由度的存在使得船体可以在三维空间中自由运动,并且能够适应不同的水上环境。
对于船员来说,了解船舶运动的六个自由度是非常重要的,因为只有了解了这些自由度,才能够更好地掌握船体运动规律,从而保证航行安全。
船舶摇摆实验解析
具体实验内容:格式样板如下,字体均用宋体。
(填空,每空1分,共25分)船舶摇摆实验1、实验目的(10)(1)测量实船的固有横摇周期。
(2)通过实验了解船舶重心对横摇周期的影响。
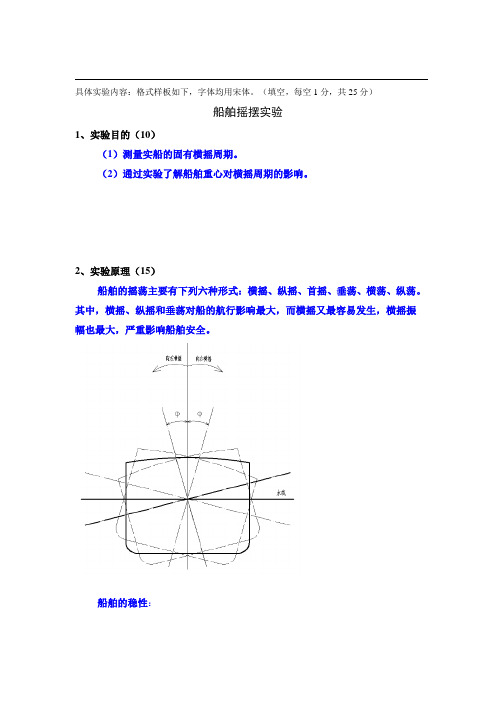
2、实验原理(15)船舶的摇荡主要有下列六种形式:横摇、纵摇、首摇、垂荡、横荡、纵荡。
其中,横摇、纵摇和垂荡对船的航行影响最大,而横摇又最容易发生,横摇振幅也最大,严重影响船舶安全。
船舶的稳性:横摇固有周期Ts:横摇摇幅衰减静水中通过对船舶施加倾斜力矩,使船舶产生初始倾角θ后,去除该力距,船舶进入自由横摇状态。
静水中船舶自由横摇的衰减曲线是按指数规律随时间而衰减的,相邻的两个横摇峰值或谷值之间的时间间隔即为横摇的固有周期Ts。
在半个周期时间间隔内,横摇幅值绝对值的变化为由以上关系可得无因次衰减系数的表达式为:3、实验步骤(10)1、确认所有实验设备处于正确的初始状态,包括:船舶(模)的摇摆运动不会受到干扰,倾角测量装置已上电并运行正常;2、每次实验前测量其初始倾角;3、运行倾角测量软件;4、给船舶施加倾斜力矩使其倾斜;5、点击倾角测量软件界面上的“开始”按钮,此时开始测量倾角数据并显示在界面上;6、去除倾斜力矩使船舶进入自由横摇状态;7、等待一定时间后,点击倾角测量软件界面上的“暂停”按钮,停止测量倾角数据;8、将记录下来的倾角数据保存在指定的文件中;9、在船舶的某一高度上增加重量。
首先将双面胶的一面贴在亚铁上,然后将亚铁粘贴到船模上。
注意沿船长的方向,亚铁的中心线要与船模的中线一致,避免船舶左右不对称产生固定的横倾角。
将增加重量的船模放入水中,给船模施加倾斜力矩使其倾斜,去除该力矩使船舶进入自由横摇状态,对船模摇摆的倾角进行测量并保存实验数据。
按照这个方法,逐渐增加亚铁的数量,并对其进行摇摆试验,测量其摇摆横倾角并保存数据;10、点击倾角测量软件界面上的“退出”按钮,关闭该软件,结束实验。
4、实验数据及其处理(40)根据测得的倾角数据绘制倾角随时间的变化曲线、船舶横摇消灭曲线,求实验船舶的横摇周期、无因次阻尼系数,并写出算例。
船舶非线性参激横摇运动的分析

总第175期水运科技信息1999年第4期收稿日期:1999205215船舶非线性参激横摇运动的分析张 兢(武汉交通科技大学航运学院 武汉 430062)摘 要 应用非线性振动理论中的摄动法,求出了描述参激横摇运动的非线性方程的解,并分析解的稳定性。
结果表明,参激横摇运动具有明显的非线性特征。
关键词 参激横摇运动 摄动法 非线性振动理论1 引言由于纵摇或垂荡对横摇的耦合作用,或由于波浪的周期性干扰,会引起横摇回复力矩的周期性变化。
这种系统内部参数的变化对系统运动的影响,称为参数激励。
由参数激励所引起的横摇运动,称为参激横摇。
在一定的条件下,参激横摇会变得不稳定,导致增幅横摇运动。
这种现象就是横摇参数共振,参激横摇运动及参数共振现象,是当前国际上关于船舶稳性和耐波性研究的热门课题之一。
描述参激横摇运动的主要数学模型是M ath ieu 方程。
但是M ath ieu 方程描述的是一个单自由度的时变线性系统。
而参激横摇是一个大摇幅的非线性问题,用线性模型来研究大角度的非线性横摇问题,显然不尽合理。
因此,本文采用非线性参激横摇运动方程作为研究的基础,用非线性振动理论中的摄动法,分析参激横摇运动的基本特性,探索它的运动规律。
2 运动方程根据船舶的受力分析,可写出下列形式的横摇运动方程:Ηβ+D (Ηα,t )+R (Η,t )=E (t )+W (t )(1)式中:t ——时间;Η——;Ηα=d Η d t ——横摇角速度;Ηβ=d 2Η d t 2——横摇角加速度。
D (Ηα)代表横摇阻尼力矩,它是横摇角速度的函数,阻尼力矩的常用模式有三种:线性模式、线性加平方模式和线性加立方模式。
本文采用第三种模式,即D (Η)=n 1Ηα+n 3Ηα3(2)式中:n 1和n 3分别为线性阻尼系数和非线性阻尼系数,通过船舶横摇衰减试验来确定。
R (Η,t )代表横摇回复力矩,它是横摇角和时间的函数。
R (Η,t )由两部分组成:第一部分是船舶在静水中的回复力矩,与时间无关。
多自由度耦合的船舶参数横摇运动分析和数值计算

多自由度耦合的船舶参数横摇运动分析和数值计算船舶的横摇运动是指船舶在水平方向上由于外界环境力的作用而发生的左右摆动运动。
对于多自由度耦合的船舶系统而言,横摇运动的分析和数值计算是一个非常复杂的问题。
这种系统的船体在不同自由度上的运动相互耦合,因此需要考虑多种因素的影响,如船体结构、载荷分布、水动力与结构动力的耦合效应等。
在进行多自由度耦合的船舶参数横摇运动分析和数值计算时,一般采用数学模型来描述船体在横摇过程中的运动。
这个数学模型通常包括船舶的结构特性、水动力和结构动力之间的相互作用等因素。
通过建立这个数学模型,可以利用物理原理和数学方法来研究船舶横摇运动的特性,比如横摇的周期、振幅、频率等。
在进行横摇运动分析时,需要考虑到船舶的多自由度耦合效应。
这种耦合效应包括船体在横滚、纵摆和横向平移等不同自由度上的运动之间的相互作用。
这些自由度之间的相互作用会对船舶的横摇运动产生影响,使得其运动变得更加复杂和难以预测。
为了进行多自由度耦合的船舶参数横摇运动的数值计算,一般采用数值求解方法。
这些方法包括有限元法、边界元法、流体-结构相互作用方法等。
通过这些数值方法,可以对船舶在横摇过程中的动态响应进行精确的计算和分析,得出船舶在不同情况下的横摇运动特性。
在进行多自由度耦合的船舶参数横摇运动分析和数值计算时,需要考虑到各种复杂因素的影响,如船舶结构的非线性特性、海洋环境的不确定性、船舶载荷的变化等。
为了能够准确地评估船舶在横摇运动中的性能和安全性,必须进行详细的分析和计算,以及充分考虑到多自由度耦合效应的影响。
综上所述,多自由度耦合的船舶参数横摇运动分析和数值计算是一个复杂而重要的问题。
只有通过对船舶系统进行深入分析和精确计算,才能更好地理解船舶在横摇过程中的运动特性,从而为船舶设计和运行提供更好的指导和保障。
破损船舶瘫船时的横摇运动分析

破 损 船 舶 瘫 船 时 的横 摇 运 动 分 析
胡丽芬 ,鲁 江 , 张全 忠 , 田忠 民
( 1 . 鲁 东大学交通 学院,烟 台 2 5 0 0 6 4 ;2 中国船舶科 学研 究中心,无锡 2 1 4 0 8 2)
摘
要
为 了研 究破损船舶瘫船 时的横 摇运动 , 采用 Da v e n p o r t 风 谱计算定 常风和 阵风 的风倾力矩 , 采用 I T T C双 参数 波谱 计算不规则波波浪力矩 ,采用增加 重量法计算破损进水 ,建 立 了破损船舶 瘫船时的横摇运动方程。 最后 以一艘船舶 为例 ,计算 了船舶 非对称破损 、对称破损 以及 完整状 态下的横 摇运 动幅值 ,分析 了破损船舶
风浪 并存 时单 自由度横 摇运 动 方程 如下 :
+
(
㈩
为 横摇惯 性 矩 ,
式中, 为横 摇 角 , 为 线性 阻尼 系数 , 为非线 性 阻尼 系数 , 为 船舶 重量 ,
为 随 时间变 化 的横摇 附加惯 性 矩 ,G z 为对 应 不 同横 倾 角 时的 复原 力臂 , 为基 于 F r o u d . Kr y l o v假 设 的波 浪激励 力 矩 。 1 . 2 . 1 风倾 力矩 计 算 风 倾 力矩 的计 算可 用下 式表 示 :
nd
. n d ( 0 为风 倾 力矩 ,
。 (
( f ) = o . s x p . C m V C
+ C m
( f )
( 2 )
式 中 ,P a i r 是空气 密 度 ,c 为空气 阻力 系数 ,
中
国
造
船
学 术论 文
空间点、海浪和船体运动关系,即空间固定坐标系o  ̄ r t (、运动坐标系G 和随船平移的参考坐标
船舶横摇运动中力矩研究分析

船舶横摇角较小的情况下可以应用线性横摇理论来研究船舶的横摇运动,将船舶看作是一个刚体,在海浪的干扰下,船体绕中心线摆动,规定从船尾向船首看,顺时针为正,逆时针为负,取船舶的横摇角为φ横摇角速度为φ,横摇角加速度为φ ,船舶在波浪中的横摇所受的力矩可以看成船舶在静水中横摇所受的力矩加上波浪的正浮状态船体的扰动力矩,为此,船舶在波浪上的横摇受以下几种力矩的作用:一、复原力矩当船舶横摇某一角度Φ时,此时浮心和重心不在同一垂线上,形成一个使船舶回复到原来位置的力矩,即复原力矩)(ΦM ,当横摇角不太大时,可以应用初稳性公式:Φ-=ΦDh M )( 式中:D 为排水量;h 为初稳性高。
二、阻尼力矩船在水中横摇,由于船体和水之间存在相对速度,船体必然受到阻力,阻尼力 矩大体受到三个原因的作用:摩擦阻尼,兴波阻尼,漩涡阻尼。
(1)摩擦阻尼它是水的粘性引起的,其数值的大小一般认为和角速度的平方成比例,在横摇中,摩擦阻尼所占的比重是很小的,往往可以忽略。
(2)兴波阻尼它是由于船的运动在水表面形成波浪,消耗了船体本身的能量而形成的,一般认为兴波阻尼比例于角速度的一次方。
(3)漩涡阻尼它是在船体弯曲或突出物附近形成漩涡,损失部分能量而形成的。
船舶横摇阻尼力矩与船体形状、装载情况、舭龙骨、横摇频率和幅值等多种因素有关,精确的确定阻尼力矩是目前横摇研究中最困难的问题。
用理论方法确定的阻尼力矩尚不能用于实际,最可靠的方法是进行实船或模型试验。
小角度横摇时,认为船舶是时间恒定的线性系统,阻尼力矩与角速度成线性关系,其计算公式如下:φφ N M z 2-= Dh J J N )(φφφφμ∆+= 其中: φN 为横摇阻尼系数;φμ为无因次横摇衰减系数;φJ 为转动惯量;φJ ∆为附加转动惯量。
三、惯性力矩船舶在横摇运动中存在角加速度,则必然会产生惯性力矩,惯性力矩两部分组成,即船舶自身的惯性力矩和附加惯性力矩,它与横摇角加速度的关系可写成:φφφφ )()(J J M ∆+-= 式中:φJ 为转动惯量;φJ ∆为附加转动惯量。
船舶耐波性总结2讲解

船舶耐波性总结第一章耐波性概述一、海浪的描述、、。
船舶耐波性是船舶在波浪中运动特性的统称,它包括船舶在波浪中所产生的各种摇荡运动以及由这些运动引起的抨击、飞溅、上浪、失速、螺旋桨飞车和波浪弯矩变化等性能,直接影响船舶在风浪作用下维持正常功能的能力。
二、6个自由度的摇荡运动船舶任意时刻的运动可以分解为在Oxyz坐标系内船舶中心G沿三个坐标轴的直线运动及船体绕三个坐标轴的转动。
而这些运动中又有直线运动和往复运动垂荡对船舶航行影响最大,是研究船舶摇荡运动的主要内容。
船舶摇荡是指船舶在风浪作用下产生的摇荡运动,他们的共同特点是在平衡位置附近做周期性的震荡作用。
产生何种摇荡运动形式取决于船首方向与风浪船舶方向之间的夹角,称为遭遇浪向。
三、动力响应船舶耐波性是船舶在风浪中性能的总的反应,它主要包括船舶摇荡、砰击、上浪、失速、螺旋桨飞车。
剧烈的横摇、纵摇和垂荡对船舶产生一系列有害的影响,甚至引起惨重后果,主要表现在以下三个方面:1)、对适居性的影响;2)、对航行使用性的影响;3)、对安全性的影响;船舶在风浪中产生摇荡运动时,船体本身具有角加速度和线加速度,因此属于非定常运动。
第二章海浪与统计分析2-1 海浪概述风浪的三要素:风速、风时、风区长度。
风浪要素定义:表观波长、表观波幅、表观周期。
充分发展海浪条件:应有足够的风时和风区长度。
海浪分类:风浪、涌浪、近岸浪。
风浪的要素表示方法:统计分析方法。
2-2规则波的特性波面可以用简单的函数表达的波浪称为规则波。
A 0=cos kx -t ξξω()A k ξξω为波面升高,为波幅,为波数,为波浪圆频率。
在深水条件下,波长T c λ、周期和波速之间存在以下关系 :≈; 2=1.56T λ; c==1.25T λλ; 2=T πω; 2k=g ω 波浪中水质点的振荡,并没有使水质点向前移动,也没用质量传递。
但是水质点具有速度且有升高,因此波浪具有能量。
余弦波单位波表面积的波浪所具有的能量2A 1E=g 2ρξ2-3不规则波理论基础一、不规则波的基本概念 1、确定性关系和统计关系我们所讨论的不规则波引起的船舶摇荡运动等都是属于统计规律范畴之内的。
船舶力矩物理知识点总结

船舶力矩物理知识点总结一、船舶力矩的定义船舶力矩是指作用在船舶上的力矩,它由船舶受到的外力和内力产生。
外力包括风力、水流力、舵杆力等,内力包括发动机推进力、舵的作用力等。
船舶力矩的大小和方向决定了船舶的转向和运动方向。
二、船舶力矩的计算船舶力矩的计算需要考虑船舶受到的外力和内力。
对于风力和水流力,可以通过测量风速和水流速度来计算其大小和方向;对于发动机推进力和舵的作用力,则可以根据推进器数据和舵的角度来计算其大小和方向。
船舶力矩的计算通常需要进行复杂的数学和物理运算,因此需要依靠计算机和专业软件来进行。
三、船舶力矩的影响船舶力矩的大小和方向直接影响着船舶的运动和操纵。
例如,当船舶受到侧风作用时,风力会产生一个侧向力矩,导致船舶偏离原来的航向;当船舶进行转向时,舵的作用力会产生一个横向力矩,导致船舶进行横向转向。
因此,船舶力矩的大小和方向是船舶操纵和稳定性的重要因素。
四、船舶力矩的调节为了保证船舶的安全和稳定性,船舶力矩需要进行及时调节。
调节船舶力矩的方法包括调整船舶的舵角、改变推进器的工作状态、调整船舶的重心位置等。
通过合理的调节,可以使船舶在各种外界环境下保持稳定的运动状态,并能进行各种操纵动作。
五、船舶力矩的应用船舶力矩的物理知识在船舶工程和航海领域有着广泛的应用。
船舶工程师通过对船舶力矩的计算和调节,可以设计出具有良好操纵性和稳定性的船舶;船员则通过熟练掌握船舶力矩的物理规律,能够进行高效、安全的航行操作。
总结船舶力矩是船舶运动中的重要物理量,它决定了船舶的操纵和稳定性。
船舶力矩的计算和调节需要依靠复杂的数学和物理原理,广泛应用于船舶工程和航海领域。
熟悉船舶力矩的物理知识,对于船舶工程师和船员来说是至关重要的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
船舶横摇角较小的情况下可以应用线性横摇理论来研究船舶的横摇运动,将船舶看作是一个刚体,在海浪的干扰下,船体绕中心线摆动,规定从船尾向船首看,
顺时针为正,逆时针为负,取船舶的横摇角为φ横摇角速度为φ
,横摇角加速度为φ ,船舶在波浪中的横摇所受的力矩可以看成船舶在静水中横摇所受的力矩加上波浪的正浮状态船体的扰动力矩,为此,船舶在波浪上的横摇受以下几种力矩的作用:
一、复原力矩
当船舶横摇某一角度Φ时,此时浮心和重心不在同一垂线上,形成一个使船舶回复到原来位置的力矩,即复原力矩)(ΦM ,当横摇角不太大时,可以应用初稳性公式:
Φ-=ΦDh M )( 式中:D 为排水量;
h 为初稳性高。
二、阻尼力矩
船在水中横摇,由于船体和水之间存在相对速度,船体必然受到阻力,阻尼力 矩大体受到三个原因的作用:摩擦阻尼,兴波阻尼,漩涡阻尼。
(1)摩擦阻尼
它是水的粘性引起的,其数值的大小一般认为和角速度的平方成比例,在横摇中,摩擦阻尼所占的比重是很小的,往往可以忽略。
(2)兴波阻尼
它是由于船的运动在水表面形成波浪,消耗了船体本身的能量而形成的,一般认为兴波阻尼比例于角速度的一次方。
(3)漩涡阻尼
它是在船体弯曲或突出物附近形成漩涡,损失部分能量而形成的。
船舶横摇阻尼力矩与船体形状、装载情况、舭龙骨、横摇频率和幅值等多种因素有关,精确的确定阻尼力矩是目前横摇研究中最困难的问题。
用理论方法确定的阻尼力矩尚不能用于实际,最可靠的方法是进行实船或模型试验。
小角度横摇时,认为船舶是时间恒定的线性系统,阻尼力矩与角速度成线性关系,其计算公式如下:
φ
φ N M z 2-= Dh J J N )(φφφφμ∆+= 其中: φN 为横摇阻尼系数;
φμ为无因次横摇衰减系数;
φJ 为转动惯量;
φJ ∆为附加转动惯量。
三、惯性力矩
船舶在横摇运动中存在角加速度,则必然会产生惯性力矩,惯性力矩两部分组成,即船舶自身的惯性力矩和附加惯性力矩,它与横摇角加速度的关系可写成:
φφφ
φ )()(J J M ∆+-= 式中:φJ 为转动惯量;
φJ ∆为附加转动惯量。
四、海浪扰动力矩
波浪改变了船体水下的体积的形状,从而产生复原扰动力矩,船体的存在阻止了波浪的运动,反之波浪也给船体一个作用力矩。
海浪扰动力矩是引起船舶横摇运动的主要原因,它由三部分组成:
(1)由于波浪改变船体水下部分体积的形状而产生的复原力矩公式为:
e BH Dh M α=
(2)海浪对船舶航行时的阻尼扰动力矩可表示为:
e BZ N M α
φ 2=
(3)船体的附加惯性扰动方矩可表示为: e BG J M α
φ ∆= 故波浪扰动力矩可表示为:
=),,(e e e M αα
α e Dh α+e N αφ 2+e J αφ ∆ 五、扶正力矩
由于减摇装置的存在,当波浪作用到船上时,减摇装置给船一个扶正力矩,以使船舶的横摇角减小,用于抵消波浪对船舶的作用力。
公式如下:
f Dh M α-=Φ)(。
