第二章船舶在规则波中的摇荡 船舶运动学教学课件
合集下载
第二章船舶在规则波中的摇荡 船舶运动学教学课件
图示:
船舶在规则横波中的线性横摇
二、横摇微分方程及解 3。关于放大因数的讨论:
物理解释: 横摇的谐摇状态:波浪周期TB等于船横摇固有周期Tθ称 为谐摇. 此时,船的横摇运动滞后波浪90°,放大因子 很大,横摇达到很大值,出现共振现象,是航行中最 危险的情况。必须引起注意。
横摇的谐摇状态
谐摇:波浪周期 TB等于船横摇 固有周期 Tθ 称为谐摇. 谐摇区:从放大因数曲线知, 不仅在谐摇 (∧θ=1 ),放大 因数 很大,而且在 ∧θ=1 附近的 一定范围内 也是 相当大 的,通常称 的范围为谐摇区.
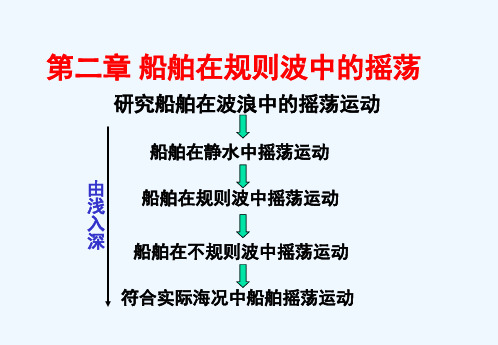
第二章 船舶在规则波中的摇荡
研究船舶在波浪中的摇荡运动
船舶在静水中摇荡运动 由 浅 入 深 船舶在规则波中摇荡运动 船舶在不规则波中摇荡运动
符合实际海况中船舶摇荡运动
重点:船舶在规则波中的线性横摇,航速航向影响. 难点:考虑非线性影响的共振横摇角计算
船舶在规则波中的摇荡
非线性共 振横摇角
一般 非线 性阻 尼共 振角 规 范 横 摇 角
第二节 船舶在规则横波中的线性横摇
船舶在规则横波中的线性横摇
一、正横波中的波浪扰动力矩
船舶受到表观重力垂直于某一深度的次波面。该次 波面称为有效波面。对应有效波倾角为αm 与表面波倾角的关系:
其中:
船舶在规则横波中的线性横摇
一、正横波中的波浪扰动力矩 有效波倾系数是 船体形状船宽与波长 之比、吃水以及重心 竖向位置的函数。理 论计算相当复杂,通 常工程上采用公式近 似估算。
二、垂荡的主干扰力和纵摇的主干扰力矩
2.纵摇的主干扰力矩
将上图微元体的垂荡干扰力的主要部分对Gyb轴取 矩,然后沿船长积分: 其中:
修正系数
船舶操纵和避碰规则PPT课件

43
四、锚与锚泊
2.锚抓力与出链长度
根据试验,当底质为泥沙时,锚的抓力于 链长、水深的关系如下表
出链长度/水深 1.5 2.0 2.5 3.0 3.5
抓力/锚在空气中 的重量
0.66
1.01
1.39
1.74
2.09
44
四、锚与锚泊
单锚泊抓力 单锚泊时的锚抓力可用下式表达: P=Pa+Pc=λwa+λwcl
+
Y (Y 2T0 ) Wc
46
四、锚与锚泊
经验公式: (1)当风速为20M/S时,出链长度为:
Lc 3H90m
(2)当风速为30M/S时,出链长度为:
Lc 4H14m 5
47
四、锚与锚泊
3.港内锚地锚泊所需水 域
单锚泊旋回半径R=船 长L+实际出链长度 Lc
船间最小安全距离 D=L2+2LC2
23
二、环境因素对操船的影响
4.岸吸与岸推 岸吸:船在狭窄航道的一侧与
陆岸平行航行时,船体与岸 壁之间流速增大,形成低压 区。螺旋桨盘面吸入流与排 出流的作用,靠岸的一边前 面的水来不及补充,水位下 降其压力较外舷低,产生岸 吸现象 岸推:船前进时推水向左右两 侧,靠岸一侧受岸壁阻挡, 扩散不开,形成高水位;另 一侧水流扩散快水位较低, 造成船首向外偏的现象。
P 1 2w C yw L w d(u y v c)2 1 2aC ya B av a 2
船舶横向水阻力
横向风压阻力
41
三、港作拖轮及其运用
所需拖轮马力的简易估算方法: 总的拖轮马力=船舶载重吨X10%
42
四、锚与锚泊
1.锚的用途 锚泊 港内用锚助操 1).抑制船速 2).控制船身横向移动 3).协助调头 4).稳住船首 应急操纵上的使用 1).避免碰撞、触礁、上滩 2).保证狭水道航行安全时使用 3).海上漂滞使用 4).系泊时缓和船体受外力的摇动 5).搁浅后固定船体以及协助脱浅
四、锚与锚泊
2.锚抓力与出链长度
根据试验,当底质为泥沙时,锚的抓力于 链长、水深的关系如下表
出链长度/水深 1.5 2.0 2.5 3.0 3.5
抓力/锚在空气中 的重量
0.66
1.01
1.39
1.74
2.09
44
四、锚与锚泊
单锚泊抓力 单锚泊时的锚抓力可用下式表达: P=Pa+Pc=λwa+λwcl
+
Y (Y 2T0 ) Wc
46
四、锚与锚泊
经验公式: (1)当风速为20M/S时,出链长度为:
Lc 3H90m
(2)当风速为30M/S时,出链长度为:
Lc 4H14m 5
47
四、锚与锚泊
3.港内锚地锚泊所需水 域
单锚泊旋回半径R=船 长L+实际出链长度 Lc
船间最小安全距离 D=L2+2LC2
23
二、环境因素对操船的影响
4.岸吸与岸推 岸吸:船在狭窄航道的一侧与
陆岸平行航行时,船体与岸 壁之间流速增大,形成低压 区。螺旋桨盘面吸入流与排 出流的作用,靠岸的一边前 面的水来不及补充,水位下 降其压力较外舷低,产生岸 吸现象 岸推:船前进时推水向左右两 侧,靠岸一侧受岸壁阻挡, 扩散不开,形成高水位;另 一侧水流扩散快水位较低, 造成船首向外偏的现象。
P 1 2w C yw L w d(u y v c)2 1 2aC ya B av a 2
船舶横向水阻力
横向风压阻力
41
三、港作拖轮及其运用
所需拖轮马力的简易估算方法: 总的拖轮马力=船舶载重吨X10%
42
四、锚与锚泊
1.锚的用途 锚泊 港内用锚助操 1).抑制船速 2).控制船身横向移动 3).协助调头 4).稳住船首 应急操纵上的使用 1).避免碰撞、触礁、上滩 2).保证狭水道航行安全时使用 3).海上漂滞使用 4).系泊时缓和船体受外力的摇动 5).搁浅后固定船体以及协助脱浅
船体振动学 PPT

Ship Vibration
0.4 振动系统 振动系统三要素:质量,刚度,阻尼。 质量(包括转动惯量)是感受惯性的元件,刚度 是感受弹性的元件,阻尼是耗能元件。
Ship Vibration
0.4 振动系统
振动系统一般可分为连续系统和离散系统。 (1)连续系统(无限多自由度系统,分布参数 系统) 结构参数(质量,刚度,阻尼等)在空间上连续 分布。弹性体是具有无限多自由度的系统,它的 振动规律要用时间和空间坐标的函数来描述,其 振动方程是偏微分方程。 (2)离散系统(多自由度系统) 结构参数为集中参量。所建立的振动方程是常微 分方程。
2梁自由振动和强迫振动的基本理论和计算方法4了解船体总振动和局部振动的力学模型的建立和计算方法5了解船体振动产生的原因6了解船体振动衡准和防振减振措施船体振动学shipvibration4参考教材翁长俭张保玉编
船体振动学
1 课程内容 2 课程目标
3 课程基本要求
4 参考教材
Ship Vibration
Ship Vibration
0.1 基本概念
各个不同领域中的振动现象虽然各有特色,但往 往有着相似的数学力学模型。正是在这种共性的 基础上,有可能建立一种统一的理论来处理各种 振动问题。 振动力学:借助数学、物理、实验和计算技术, 探讨各种振动现象,阐明振动的基本规律,以便 克服振动的消极因素,利用振动的积极因素,为 合理解决各种振动问题提供理论依据。
Ship Vibration
0.5 振动问题的分类
按激励特性来划分: (1)自由振动 没有外部激励,或者外部激励消失后,系统自身 的振动。 (2)强迫振动 系统在作为时间函数的外部激励下发生的振动, 这种外部激励不受系统运动的影响。 (3)自激振动 系统受其自身运动诱发出来的激励的作用而产生 和维持的振动,例如小提琴发出的乐声,飞机机 翼的颤振等。
《船舶操纵》课件

4) 旋回直径(final diameter)
旋回直径是指船舶作定常旋回时重心轨迹圆的直径, 亦称旋回终径,并以D表示之,它大约为旋回初径的 0.9~ 1.2倍。 5) 滞距(reach)
亦称心距。正常旋回时,船舶旋回直径的中心 O 总较操 舵时船舶重心位置更偏于前方。滞距是该中心 O 的纵距,并 以Re代表之,大约为1~2倍船长,它表示操舵后到船舶进入 旋回的“滞后距离”,也是衡量船舶舵效的标准之一。
二节 船舶操纵方程及船舶操纵性指数
一、船舶操纵运动方程
Tŕ+r=Kδ
式中:K —— 旋回性指数(s-1); T —— 追随性指数(s); r —— 旋回角速度(1/s); ŕ —— 旋回角加速度(1/s2);
δ —— 舵角(°)。
该方程最早是由日本学者野本谦作提出的,因此也称为 野本方程。该式中,T称之为船舶的追随性指数(turning lag index), 单 位 为 s;K 称 之 为 船 舶 的 旋 回 性 指 数 ( turning ability index)。
11.螺旋桨的转动方向
由于受螺旋桨横向力的影响,船舶向左或向右旋回时的旋回 圈的大小将有所不同。对于右旋固定螺距螺旋桨单车船而言,
在其他条件相同的情况下,向左旋回时的旋回初径要比向右 旋回时的旋回初径要小一些。但对于超大型船舶而言,这一 差别很小。 另外,船体的污底、风、流的作用都将对船舶旋回圈 的大小产生影响。例如顶风、顶流使旋回圈进距减小,顺风、 顺流使旋回圈进距增大等等。
四、旋回圈要素在实际操船中的应用
由旋回试验测定的旋回圈资料是船舶操纵性能的重要 内容之一,它不仅用来评价船舶的旋回性能,同时还可以 直接用于实际操船。
1.旋回初径、进距、横距、滞距和在实际操船 中的应用
船舶操纵-PPT课件

2.2 船舶操纵运动方程
野本方程
操舵速度有限,船舶的惯性很大,船舶对舵的 响应也是一种非常缓慢的运动,因此有
建立了有效的数学研究方法,借鉴飞艇操纵理论
1939,巴辛
利用里亚谱诺夫运动稳定理论研究船舶的运动稳定 性
1.1 船舶操纵性总论
船舶操纵性研究的发展过程
1944,肯夫(kemf)
提出了用Z形操舵试验来评价船舶的操纵性,开创了 船舶对操舵的动态响应研究
1946,戴维逊(K. S. Davidson)和许夫(L. I. Schiff)
1.1 操纵性总论
操纵性的重要意义(经济性要求)
在海上的直航运动,
航向稳定性好 不用经常地去操舵,航迹接近直线
不好的船 频繁操舵纠正航向,经历曲折的航线,增加了实际 的航行距离,同时增加了操纵装置和推进装置的功 率消耗 由于操舵增加的功率消耗占主机功率的2%-3%,航 向稳定性不好的船,可以高达20%。
船舶有横漂速度 时横向力的导数。该力很大, 方向与 相反;
船舶有横漂速度 时横向力对重心力矩的导数。 该力矩不太大,为负值,方向有使漂角增大的趋势;
船舶有前进速度 时纵向力的导数。该力较小, 方向与 相反。
2.2 船舶操纵运动方程
水动力导数的物理意义
水动力和力矩的旋转导数 和
船首具有右舷攻角,产生负的水动力和负的水动力 矩
– 该时刻船舶运动状态决定的水动力 – 该时刻以前的运动历史决定的水动力
其他原因引起的外力,如托缆力和风压力等;
2.2 操纵运动方程的线性化
水动力学数学模型
船舶静水中运动时的受力,采用一阶泰勒展开
2.2 操纵运动方程的线性化
波浪载荷讲义

第三章 波浪中的船舶运动与三维线性势流理论
三维线性势流理论是深入研究船舶在波浪中的运动与波浪载荷特性所必备的基础知识。 本章将扼要阐述船舶在规则波中的运动与流场速度势的表示, 非定常扰动势的定解条件与面 元法,船舶运动的稳态解与波浪诱导载荷计算等内容。 3.1 船舶在规则波中的运动与流场速度势的表示 3.1.1 基本假定 在势流理论中,通常引入下述基本假定: ① 认为流体是不可压缩的理性流体,其表面张力效应可忽略不计; ② 运动是无旋的,即存在速度势 Φ ( x, y , z, t ) ,其梯度 ∇Φ ( x, y , z, t ) 给出流体质点的速度 矢量。 于是,可采用速度势的方法来研究波浪以及船舶在波浪中的运动。 在线性理论中,所考察的波浪是微幅波。此外,为简单计,通常还认为水域底部以光滑 水平壁面为界,水深为常数;并假定水中没有流。 3.1.2 船舶在规则波中的运动 设船舶在微幅规则波中以一定的航速和航向行驶, 由于波浪的扰动而引起船舶的摇荡运
船舶波浪载荷
目录
第一章 ቤተ መጻሕፍቲ ባይዱ论 第二章 海浪
2.1 海浪谱的表达式 2.1.1 频率谱式 2.1.2 方向谱式 2.2 海浪长期统计资料的选用 2.2.1 世界各主要船级社所采用的海浪长期统计资料 2.2.2 1991 年 IACS 推荐的标准海浪资料 No.34 2.2.3 九十年代后期海浪长期统计资料研究工作的新进展 2.3 影响我国船体设计的几个主要海浪统计资料
第七章 波浪载荷设计值
7.1 确定波浪载荷设计值的原则
7.2 7.3 7.4 7.5 7.6
剖面波浪载荷的设计值 低频波浪载荷分量之间的组合 砰击载荷的设计值 极限强度校核中的波浪载荷 疲劳强度分析中的波浪载荷
第八章 船舶波浪载荷的试验研究
船舶在波浪中的运动理论-ch2_海洋波浪理论1

or 0 z zh
在上述假设下,对波动问题相应的分析处理思想及方法称为
小振幅波理论、线性波理论、正弦波理论、Airy波理论。
LECTURE NOTES :OCEAN WAVE THEORY
15
§2.2 水波理论
——平面波
先考虑一种简单的平面驻波:仅沿x方向传播,y方向各截面内
的波动均相同,
a cos(kx t)
LECTURE NOTES :OCEAN WAVE THEORY
§2.2 水波理论
——小振幅波理论
若波动的波幅 a与波长 相比为小量,即 a 1 ,并注 意到未知的自由面与静水面z=0 的差别为O() ,从而微幅波的定解
问题归结为:
2 0
(p )
2 t 2
g
z
0
(z 0)
zh 0
h 2 kg
zLeabharlann x; txo
LECTURE NOTES :OCEAN WAVE THEORY
20
§2.2 水波理论
流场速度分布:
V
——平面波基本特性
(x, z;t) g a ekz sin(kx t) (x, z;t) g a ekz sin kxcost
质 点 运 动 轨 迹 : (x x0 )2 (z z0 )2 ( aekz0 )2
LECTURE NOTES:
船舶在波浪中的运动理论
Theory of Ship Motions in Waves
CH2. 海洋波浪理论
Ocean Wave Theory
本章内容:
2.1 海洋波浪概述 2.2 水波理论基础
定解问题、线性与非线性水波、水波运动特征
2. 3 风浪
11船舶在静水中的摇荡

I x1 Dh 0
用Ix1除上式两边,则得: Dh 0 I x1 令 Dh 2
I x1
n
(11-4)
2 则自由横摇方程可写成: n 0 其解可表达为: (t ) C1 cos n t C2 sin n t
Steady heel angle
船海系:邱磊
Actual ship configuration
《船舶操纵性与耐波性》课件
船海系:邱磊
浮心的移动(Displacement of the center of buoyancy)
《船舶操纵性与耐波性》课件
船海系:邱磊
浮心的移动(Displacement of the center of buoyancy)
船海系:邱磊
惯性矩近似估算公式
《船舶操纵性与耐波性》课件
2.什曼斯基公式
(11-15)
船海系:邱磊
惯性矩近似估算公式
《船舶操纵性与耐波性》课件
3.惯性半径法。
(11-16)
船海系:邱磊
惯性矩近似估算公式
《船舶操纵性与耐波性》课件
4.加藤公式
加藤根据 实船的测量结果得到的经验公式:
(11-21)
船海系:邱磊
-、横摇受力分析
《船舶操纵性与耐波性》课件
2.惯性力矩
横摇由于是变速运动,所以产生了对横摇轴的惯性力矩。 另一方面横摇使船舶周围的水也得到了加速,船体必定给 予流体一定的作用力矩。根据作用与反作用原理,流体对 于船体也有一个反作用力矩,这个反作用力矩叫附加惯性 力矩。因此,船舶在静水中横摇时的惯性力矩由两部分组 成:船体本身的惯性力矩和附加惯性力矩。它们都是角加 速度的函数,可以写成: (11-2) M ( ) I I I
用Ix1除上式两边,则得: Dh 0 I x1 令 Dh 2
I x1
n
(11-4)
2 则自由横摇方程可写成: n 0 其解可表达为: (t ) C1 cos n t C2 sin n t
Steady heel angle
船海系:邱磊
Actual ship configuration
《船舶操纵性与耐波性》课件
船海系:邱磊
浮心的移动(Displacement of the center of buoyancy)
《船舶操纵性与耐波性》课件
船海系:邱磊
浮心的移动(Displacement of the center of buoyancy)
船海系:邱磊
惯性矩近似估算公式
《船舶操纵性与耐波性》课件
2.什曼斯基公式
(11-15)
船海系:邱磊
惯性矩近似估算公式
《船舶操纵性与耐波性》课件
3.惯性半径法。
(11-16)
船海系:邱磊
惯性矩近似估算公式
《船舶操纵性与耐波性》课件
4.加藤公式
加藤根据 实船的测量结果得到的经验公式:
(11-21)
船海系:邱磊
-、横摇受力分析
《船舶操纵性与耐波性》课件
2.惯性力矩
横摇由于是变速运动,所以产生了对横摇轴的惯性力矩。 另一方面横摇使船舶周围的水也得到了加速,船体必定给 予流体一定的作用力矩。根据作用与反作用原理,流体对 于船体也有一个反作用力矩,这个反作用力矩叫附加惯性 力矩。因此,船舶在静水中横摇时的惯性力矩由两部分组 成:船体本身的惯性力矩和附加惯性力矩。它们都是角加 速度的函数,可以写成: (11-2) M ( ) I I I
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
五、表观重力
1.流体质点受力分析 质 点 A 重力 离心惯性力 水的支持力
2.数学关系(封闭三角形) Nhomakorabea规则余弦波
五、表观重力
3.表观重力 质点A所受的合力R其方向垂直于波面,合力沿着 波面的法线方向,此合力R称为表观重力。 结论:如图所示,波面上任何位置的质点的表观
重力沿着波面的法向方向。
第二章 船舶在规则波中的摇荡
第二章 船舶在规则波中的摇荡
研究船舶在波浪中的摇荡运动
船舶在静水中摇荡运动 由 浅 入 深 船舶在规则波中摇荡运动 船舶在不规则波中摇荡运动
符合实际海况中船舶摇荡运动
重点:船舶在规则波中的线性横摇,航速航向影响. 难点:考虑非线性影响的共振横摇角计算
船舶在规则波中的摇荡
非线性共 振横摇角
一般 非线 性阻 尼共 振角 规 范 横 摇 角
例如,某海区出现的波长为60m,其波浪周期: =6.25S,那么设计在该海区航行的船舶
其横摇固有周期应为:
例
沿海λ= 60 m,T =6.2 S, 有效波倾 αm0 = 4°, 2μ= 0.15 如果 Tθ = 6.2 S, 则 θa = αm0/2μ=26° 改变设计Tθ =1.3* 6.2 =8.1秒 即∧θ= 1.3
船舶在规则横波中的线性横摇
二、横摇微分方程及解 2。求解方程:
其中: 为横摇角与波倾角的相位差 为波浪频率 将特解对时间求一次和二次导数,原方程整理可得:
船舶在规则横波中的线性横摇
二、横摇微分方程及解 2。求解方程:
由上可得横摇角: 其中: (调谐因数) (无因次衰减系数)
结论:已知无因次衰减系数和有效波倾可求横摇角。 相位角: 定义放大因数:横摇幅 值与有效波倾之比。
放大因数曲线
~
相位角随调协因数变化曲线
船舶在规则横波中的线性横摇
二、横摇微分方程及解
3。关于放大因数的讨论:
物理解释:波浪很长,初稳性高很大,横摇固 有周期很小,横摇角等于波面角。 图示: 随波逐流
船舶在规则横波中的线性横摇
二、横摇微分方程及解 3。关于放大因数的讨论:
物理解释:船处在很短的波浪上,不会发生横摇。
0.7<∧θ<1.3
0.7 谐摇区 1.3
∧θ
设计横摇固有周期
海洋的波浪周期是有一定范围的,根据大量的统计资料可知, 波浪周期大于10s以上的比较罕见,短周期波浪出现较多。因此, 在船舶设计中,必须根据船舶航行海区的波浪情况,确定船舶的 固有周期。一般使船舶的固有周期尽量大些好,以避免共振横摇 的发生。大致取 ∧θ=(Tθ / TB )>1.3。
Very low damped :Resonance
n
Heavily damped Lightly damped Frequency
第二章 船舶在规则波中的摇荡
第三节 非线性共振横摇角的确定
= 5.8°
改善横摇性能措施
(1)使Tθ远离 TB,避开共振区。 设计时,尽量使 Tθ > 1.3 TB
(2)增加横摇阻尼
减缓共振区振幅。
安装舭龙骨,减摇鳍等
Bilge Keels
Fin Stabilizer
强迫振荡
External Force, Motion, Resonance with damper
它为波浪扰动力矩的主要部分
船舶在规则横波中的线性横摇
二、横摇微分方程及解 1。横摇方程:
整理 其中:
解的分析:上述二阶常系数非齐次线性微分方程 的解为其对应的齐次微分方程的通解加上原方程的一 个特解。通解为静水中有阻尼横摇情况,由于阻尼的 存在,自由振荡随时间衰减,当t 增大时只剩下特解。即 为与波浪同频率的强迫振荡.
波 浪 扰 动 力 矩
第二章 船舶在规则波中的摇荡
第一节 规则余弦波
规则余弦波
定义:波面可以用简单函数表达的波浪称为规则波, 而波形轮廓是余弦曲线的规则波为余弦波。 余弦波的波面方程:
波的空间记录
波的时间记录
规则余弦波
一、余弦波的几何参数及参数关系
波高
规则余弦波
二、深水条件下的参数关系
规则余弦波
规则波简介
规 则 波 要 素 1。质点 轨圆运动 2。波内压 力场 3。表观重 力
线性横摇
横摇 方程 及解 ‘放 大因 数概 念
迎浪纵摇 和垂荡
纵 摇 垂 荡 主 干 扰 力 纵摇 垂荡 运动 方程 及解
航速、航 向影响
遭遇 频率 概念 对干 扰力 频率 幅值 影响 斜 浪 斜 中 斜 线 性 浪 放 大 因 数
波倾几何描述
船舶在规则横波中的线性横摇
一、正横波中的波浪扰动力矩
(基于单纯横摇方程的受力假定)
• 纯横波,即波峰线平行于船体中线面;
• 船宽远小于波长;
• 横摇角较小,符合初稳性范围; • 入射波流场不受船体存在的影响;
船舶在规则横波中的线性横摇
一、正横波中的波浪扰动力矩 (确定力矩)
船体固定,有效波 面改变了水下体积的形 状所产生的复原扰动力 矩。
图示:
船舶在规则横波中的线性横摇
二、横摇微分方程及解 3。关于放大因数的讨论:
物理解释: 横摇的谐摇状态:波浪周期TB等于船横摇固有周期Tθ称 为谐摇. 此时,船的横摇运动滞后波浪90°,放大因子 很大,横摇达到很大值,出现共振现象,是航行中最 危险的情况。必须引起注意。
横摇的谐摇状态
谐摇:波浪周期 TB等于船横摇 固有周期 Tθ 称为谐摇. 谐摇区:从放大因数曲线知, 不仅在谐摇 (∧θ=1 ),放大 因数 很大,而且在 ∧θ=1 附近的 一定范围内 也是 相当大 的,通常称 的范围为谐摇区.
第二节 船舶在规则横波中的线性横摇
船舶在规则横波中的线性横摇
一、正横波中的波浪扰动力矩
船舶受到表观重力垂直于某一深度的次波面。该次 波面称为有效波面。对应有效波倾角为αm 与表面波倾角的关系:
其中:
船舶在规则横波中的线性横摇
一、正横波中的波浪扰动力矩 有效波倾系数是 船体形状船宽与波长 之比、吃水以及重心 竖向位置的函数。理 论计算相当复杂,通 常工程上采用公式近 似估算。
三、波浪运动参数定义
波浪运动是水质点沿圆形轨道匀速运动构成的。 该运动被成为轨圆运动,轨圆运动周期即为波浪周期, 它的角速度即为波浪圆频率。 轨 圆 运 动
深水和浅水中的水质点轨迹
深水
浅水
规则余弦波
四、史密斯效应
1.
结 论
2.
“史密斯效应”
波浪下任一点动压力随深 度按指数递减的规律
规则余弦波
1.流体质点受力分析 质 点 A 重力 离心惯性力 水的支持力
2.数学关系(封闭三角形) Nhomakorabea规则余弦波
五、表观重力
3.表观重力 质点A所受的合力R其方向垂直于波面,合力沿着 波面的法线方向,此合力R称为表观重力。 结论:如图所示,波面上任何位置的质点的表观
重力沿着波面的法向方向。
第二章 船舶在规则波中的摇荡
第二章 船舶在规则波中的摇荡
研究船舶在波浪中的摇荡运动
船舶在静水中摇荡运动 由 浅 入 深 船舶在规则波中摇荡运动 船舶在不规则波中摇荡运动
符合实际海况中船舶摇荡运动
重点:船舶在规则波中的线性横摇,航速航向影响. 难点:考虑非线性影响的共振横摇角计算
船舶在规则波中的摇荡
非线性共 振横摇角
一般 非线 性阻 尼共 振角 规 范 横 摇 角
例如,某海区出现的波长为60m,其波浪周期: =6.25S,那么设计在该海区航行的船舶
其横摇固有周期应为:
例
沿海λ= 60 m,T =6.2 S, 有效波倾 αm0 = 4°, 2μ= 0.15 如果 Tθ = 6.2 S, 则 θa = αm0/2μ=26° 改变设计Tθ =1.3* 6.2 =8.1秒 即∧θ= 1.3
船舶在规则横波中的线性横摇
二、横摇微分方程及解 2。求解方程:
其中: 为横摇角与波倾角的相位差 为波浪频率 将特解对时间求一次和二次导数,原方程整理可得:
船舶在规则横波中的线性横摇
二、横摇微分方程及解 2。求解方程:
由上可得横摇角: 其中: (调谐因数) (无因次衰减系数)
结论:已知无因次衰减系数和有效波倾可求横摇角。 相位角: 定义放大因数:横摇幅 值与有效波倾之比。
放大因数曲线
~
相位角随调协因数变化曲线
船舶在规则横波中的线性横摇
二、横摇微分方程及解
3。关于放大因数的讨论:
物理解释:波浪很长,初稳性高很大,横摇固 有周期很小,横摇角等于波面角。 图示: 随波逐流
船舶在规则横波中的线性横摇
二、横摇微分方程及解 3。关于放大因数的讨论:
物理解释:船处在很短的波浪上,不会发生横摇。
0.7<∧θ<1.3
0.7 谐摇区 1.3
∧θ
设计横摇固有周期
海洋的波浪周期是有一定范围的,根据大量的统计资料可知, 波浪周期大于10s以上的比较罕见,短周期波浪出现较多。因此, 在船舶设计中,必须根据船舶航行海区的波浪情况,确定船舶的 固有周期。一般使船舶的固有周期尽量大些好,以避免共振横摇 的发生。大致取 ∧θ=(Tθ / TB )>1.3。
Very low damped :Resonance
n
Heavily damped Lightly damped Frequency
第二章 船舶在规则波中的摇荡
第三节 非线性共振横摇角的确定
= 5.8°
改善横摇性能措施
(1)使Tθ远离 TB,避开共振区。 设计时,尽量使 Tθ > 1.3 TB
(2)增加横摇阻尼
减缓共振区振幅。
安装舭龙骨,减摇鳍等
Bilge Keels
Fin Stabilizer
强迫振荡
External Force, Motion, Resonance with damper
它为波浪扰动力矩的主要部分
船舶在规则横波中的线性横摇
二、横摇微分方程及解 1。横摇方程:
整理 其中:
解的分析:上述二阶常系数非齐次线性微分方程 的解为其对应的齐次微分方程的通解加上原方程的一 个特解。通解为静水中有阻尼横摇情况,由于阻尼的 存在,自由振荡随时间衰减,当t 增大时只剩下特解。即 为与波浪同频率的强迫振荡.
波 浪 扰 动 力 矩
第二章 船舶在规则波中的摇荡
第一节 规则余弦波
规则余弦波
定义:波面可以用简单函数表达的波浪称为规则波, 而波形轮廓是余弦曲线的规则波为余弦波。 余弦波的波面方程:
波的空间记录
波的时间记录
规则余弦波
一、余弦波的几何参数及参数关系
波高
规则余弦波
二、深水条件下的参数关系
规则余弦波
规则波简介
规 则 波 要 素 1。质点 轨圆运动 2。波内压 力场 3。表观重 力
线性横摇
横摇 方程 及解 ‘放 大因 数概 念
迎浪纵摇 和垂荡
纵 摇 垂 荡 主 干 扰 力 纵摇 垂荡 运动 方程 及解
航速、航 向影响
遭遇 频率 概念 对干 扰力 频率 幅值 影响 斜 浪 斜 中 斜 线 性 浪 放 大 因 数
波倾几何描述
船舶在规则横波中的线性横摇
一、正横波中的波浪扰动力矩
(基于单纯横摇方程的受力假定)
• 纯横波,即波峰线平行于船体中线面;
• 船宽远小于波长;
• 横摇角较小,符合初稳性范围; • 入射波流场不受船体存在的影响;
船舶在规则横波中的线性横摇
一、正横波中的波浪扰动力矩 (确定力矩)
船体固定,有效波 面改变了水下体积的形 状所产生的复原扰动力 矩。
图示:
船舶在规则横波中的线性横摇
二、横摇微分方程及解 3。关于放大因数的讨论:
物理解释: 横摇的谐摇状态:波浪周期TB等于船横摇固有周期Tθ称 为谐摇. 此时,船的横摇运动滞后波浪90°,放大因子 很大,横摇达到很大值,出现共振现象,是航行中最 危险的情况。必须引起注意。
横摇的谐摇状态
谐摇:波浪周期 TB等于船横摇 固有周期 Tθ 称为谐摇. 谐摇区:从放大因数曲线知, 不仅在谐摇 (∧θ=1 ),放大 因数 很大,而且在 ∧θ=1 附近的 一定范围内 也是 相当大 的,通常称 的范围为谐摇区.
第二节 船舶在规则横波中的线性横摇
船舶在规则横波中的线性横摇
一、正横波中的波浪扰动力矩
船舶受到表观重力垂直于某一深度的次波面。该次 波面称为有效波面。对应有效波倾角为αm 与表面波倾角的关系:
其中:
船舶在规则横波中的线性横摇
一、正横波中的波浪扰动力矩 有效波倾系数是 船体形状船宽与波长 之比、吃水以及重心 竖向位置的函数。理 论计算相当复杂,通 常工程上采用公式近 似估算。
三、波浪运动参数定义
波浪运动是水质点沿圆形轨道匀速运动构成的。 该运动被成为轨圆运动,轨圆运动周期即为波浪周期, 它的角速度即为波浪圆频率。 轨 圆 运 动
深水和浅水中的水质点轨迹
深水
浅水
规则余弦波
四、史密斯效应
1.
结 论
2.
“史密斯效应”
波浪下任一点动压力随深 度按指数递减的规律
规则余弦波
