浙江省宁波市2020年中考数学模拟卷

浙江省宁波市2020年中考数学模拟卷

一、选择题(每小题4分，共48分，在每小题给出的四个选项中，只有一项符合题目要求)

1． 5的绝对值是( )

A．5 B．﹣5 C．D．﹣

2．下列算式中，计算结果为a5的是( )

A．a2?a3B．(a2)3C．a2+a3D．a4÷a

3．某市决定为全市中小学教室安装空调，今年预计投入资金126000000元，其中数字126000000用科学记数法可表示为( )

A．12.6×107B．1.26×108C．1.26×109D．0.126×1010

4．函数y＝中的自变量x的取值范围是( )

A．x≠B．x≥1 C．x＞D．x≥

5．如图的几何体由六个相同的小正方体搭成，它的主视图是( )

A．B．

C．D．

6．一次数学测试，某小组5名同学的成绩统计如下(有两个数据被遮盖)：

组员甲乙丙丁戊平均成绩众数

得分81 77 ■80 82 80 ■

则被遮盖的两个数据依次是( )

A．80，2 B．81，80 C．80，80 D．81，2

7．下列命题中假命题是( )

A．对顶角相等B．直线y＝x﹣5不经过第二象限

C．五边形的内角和为540°D．因式分解x3+x2+x＝x(x2+x)

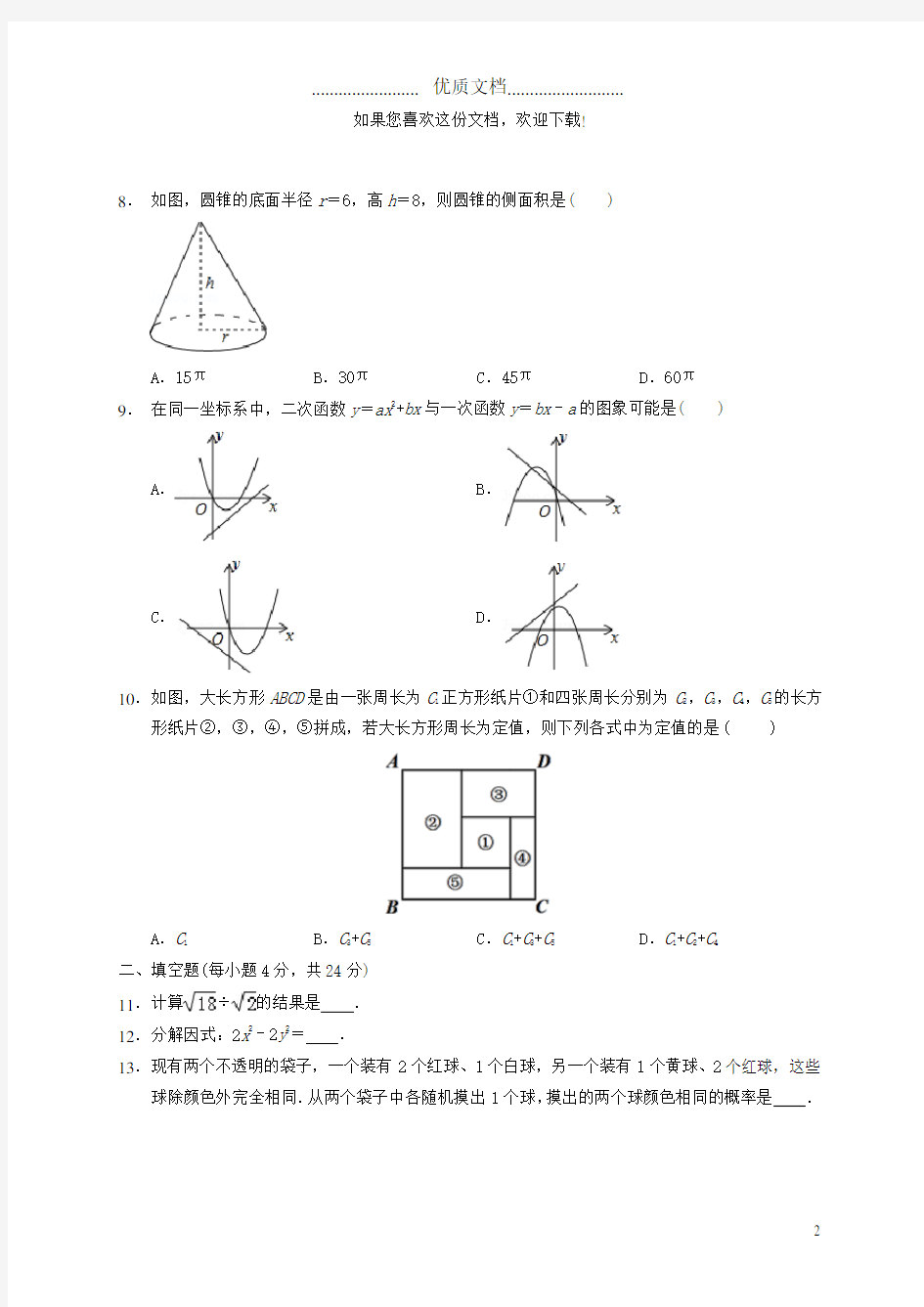
8．如图，圆锥的底面半径r＝6，高h＝8，则圆锥的侧面积是( )

A．15πB．30πC．45πD．60π

9．在同一坐标系中，二次函数y＝ax2+bx与一次函数y＝bx﹣a的图象可能是( ) A．B．

C．D．

10．如图，大长方形ABCD是由一张周长为C1正方形纸片①和四张周长分别为C2，C3，C4，C5的长方形纸片②，③，④，⑤拼成，若大长方形周长为定值，则下列各式中为定值的是( )

A．C1B．C3+C5C．C1+C3+C5D．C1+C2+C4

二、填空题(每小题4分，共24分)

11．计算÷的结果是．

12．分解因式：2x2﹣2y2＝．

13．现有两个不透明的袋子，一个装有2个红球、1个白球，另一个装有1个黄球、2个红球，这些球除颜色外完全相同．从两个袋子中各随机摸出1个球，摸出的两个球颜色相同的概率是．

14．如图，在P 处利用测角仪测得某建筑物AB 的顶端B 点的仰角为60°，点C 的仰角为45°，点

P 到建筑物的距离为PD ＝20米，则BC ＝ 米．

15．如图，ABCD Y 的对角线AC ，BD 交于点O ，AC =10，∠DAC =45°，∠BAC =30°，P 是线段AO 上

一动点，⊙P 的半径为1，当⊙P 与ABCD Y 的边相切时，AP 的长为________．

16．如图，平面直角坐标系中，A (﹣8，0)，B (﹣8，4)，C (0，4)，反比例函数y ＝的图象分别与

线段AB ，BC 交于点D ，E ，连接DE ．若点B 关于DE 的对称点恰好在OA 上，则k ＝________．

三、解答题(本大题有8小题，共78分)

17．(本题6分)先化简，再从﹣1、2、3、4中选一个合适的数作为x 的值代入求值．

(﹣)÷

C

18．(本题8分)图1、2是两张形状和大小完全相同的方格纸，方格纸中每个小正方形的边长均为1，线段AC的两个端点均在小正方形的顶点上．

(1)在图1中画出以AC为底边的等腰直角三角形ABC，点B在小正方形顶点上；

(2)在图2中画出以AC为腰的等腰三角形ACD，点D在小正方形的顶点上，且△ACD的面积为8．

19．(本题8分)某校为了解初中学生每天在校体育活动的时间(单位：h)，随机调查了该校的部分初中学生．根据调查结果，绘制出如下的统计图①和图②．请根据相关信息，解答下列问题：

(1)本次接受调查的初中学生人数为，图①中m的值为；

(2)求统计的这组每天在校体育活动时间数据的平均数、众数和中位数；

(3)根据统计的这组每天在校体育活动时间的样本数据，若该校共有800名初中学生，估计该校

每天在校体育活动时间大于1h的学生人数．

20．(本题10分)如图，矩形ABCD 中，点E 在边CD 上，将△BCE 沿BE 折叠，点C 落在AD 边上的点

F 处，过点F 作F

G ∥CD 交BE 于点G ，连接CG ．

(1) 求证：四边形CEFG 是菱形；

(2) 若AB ＝6，AD ＝10，求四边形CEFG 的面积．

21．(本题10分)抛物线21y ax c =+与x 轴交于A 、B 两点，与y 轴交于点C ，点P 在抛物线上，过

P (1，-3)，B (4，0)两点作直线2y kx b =+．

(1) 求a 、c 的值；

(2) 根据图象直接写出12y y >时，x 的取值范围；

(3) 在抛物线上是否存在点M ，使得S △ABP =5S △A BM ，若存在，求出点M 的坐标，若不存在，请说明理由．

22．(本题10分)某工厂计划生产甲、乙两种产品共2500吨，每生产1吨甲产品可获得利润0.3万元，每生产1吨乙产品可获得利润0.4万元．设该工厂生产了甲产品x(吨)，生产甲、乙两种产品获得的总利润为y(万元)．

(1)求y与x之间的函数表达式；

(2)若每生产1吨甲产品需要A原料0.25吨，每生产1吨乙产品需要A原料0.5吨．受市场影

响，该厂能获得的A原料至多为1000吨，其它原料充足．求出该工厂生产甲、乙两种产品各为多少吨时，能获得最大利润．

23．(本题12分)

【概念认识】

城市的许多街道是相互垂直或平行的，因此，往往不能沿直线行走到达目的地，只能按直角拐弯的方式行走．可以按照街道的垂直和平行方向建立平面直角坐标系xOy，对两点A(x1，y1)和B(x2，y2)，用以下方式定义两点间距离：d(A，B)＝|x1﹣x2|+|y1﹣y2|．

【数学理解】

(1)①已知点A(﹣2，1)，则d(O，A)＝．

②函数y＝﹣2x+4(0≤x≤2)的图象如图①所示，B是图象上一点，d(O，B)＝3，则点B的坐

标是．

(2)函数y＝(x＞0)的图象如图②所示．求证：该函数的图象上不存在点C，使d(O，C)＝3．

(3)函数y＝x2﹣5x+7(x≥0)的图象如图③所示，D是图象上一点，求d(O，D)的最小值及对应的

点D的坐标．

【问题解决】

(4)某市要修建一条通往景观湖的道路，如图④，道路以M为起点，先沿MN方向到某处，再在

该处拐一次直角弯沿直线到湖边，如何修建能使道路最短？(要求：建立适当的平面直角坐标系，画出示意图并简要说明理由)

24．(本题14分)如图1，平面直角坐标系xOy中，点A(0，2)，B(1，0)，C(﹣4，0)点D为射线AC 上一动点，连结BD，交y轴于点F，⊙M是△ABD的外接圆，过点D的切线交x轴于点E．

(1)判断△ABC的形状；

(2)当点D在线段AC上时，

①证明：△CDE∽△ABF；

②如图2，⊙M与y轴的另一交点为N，连结DN、BN，当四边形ABND为矩形时，求tan∠DBC；

(3)点D在射线AC运动过程中，若

1

3

CD

CA

，求

DE

DF

的值．

答案四、选择题

五、填空题

六、解答题

17．解：原式＝[﹣]÷

＝[﹣]）÷

＝?

＝x+2

∵x﹣2≠0，x﹣4≠0，

∴x≠2且x≠4，

∴当x＝﹣1时，

原式＝﹣1+2＝1．

18．解；（1）作AC的垂直平分线，作以AC为直径的圆，垂直平分线与圆的交点即为点B；

（2）以C为圆心，AC为半径作圆，格点即为点D；

19．解：（1）本次接受调查的初中学生人数为：4÷10%＝40，

m%＝＝25%，

故答案为：40，25；

（2）平均数是：＝1.5，

众数是1.5，中位数是1.5；

（3）800×＝720（人），

答：该校每天在校体育活动时间大于1h的学生有720人．

20．解：（1）证明：由题意可得，

△BCE≌△BFE，

∴∠BEC ＝∠BEF ，FE ＝CE ， ∵FG ∥CE ， ∴∠FGE ＝∠CEB ， ∴∠FGE ＝∠FEG ， ∴FG ＝FE ， ∴FG ＝EC ，

∴四边形CEFG 是平行四边形， 又∵CE ＝FE ，

∴四边形CEFG 是菱形；

（2）∵矩形ABCD 中，AB ＝6，AD ＝10，BC ＝BF ， ∴∠BAF ＝90°，AD ＝BC ＝BF ＝10， ∴AF ＝8， ∴DF ＝2，

设EF ＝x ，则CE ＝x ，DE ＝6﹣x ， ∵FDE ＝90°， ∴22

+（6﹣x ）2

＝x 2

， 解得，x ＝，

∴CE ＝

，

∴四边形CEFG 的面积是：CE ?DF ＝×2＝

21．解：（1）将P (1，－3)、B (4，0)代入y ＝ax 2

＋c 得

160

0a c a c +=??

+=?

， 1分 解得15165a c ?=????=-??

.3分

（2）由图像得x ＞4或者x ＜1 5分 （3）由S △ABP =5S △A BM 得

11

522

P M AB y AB y ??=?? 又∵P （1，-3）

得3

5

M y =

6分 231163

y 5555

M x =-=当时，即

x ∴=

得13

)5M ,23()5

M

231163

y 5555

M x =--=-当时，即

x ∴=

得33

)5M -,43()5

M -

所以13)5M 23()5M 33)5M -43()5

M -10分（每个坐标一分）

22．解：（1）y ＝0.3x +0.4（2500﹣x ）＝﹣0.1x +1000 因此y 与x 之间的函数表达式为：y ＝﹣0.1x +1000． （2）由题意得：

∴1000≤x ≤2500 又∵k ＝﹣0.1＜0 ∴y 随x 的增大而减少

∴当x ＝1000时，y 最大，此时2500﹣x ＝1500，

因此，生产甲产品1000吨，乙产品1500吨时，利润最大．

23．解：（1）①由题意得：d（O，A）＝|0+2|+|0﹣1|＝2+1＝3；

②设B（x，y），由定义两点间的距离可得：|0﹣x|+|0﹣y|＝3，

∵0≤x≤2，

∴x+y＝3，

∴，

解得：，

∴B（1，2），

故答案为：3，（1，2）；

（2）假设函数的图象上存在点C（x，y）使d（O，C）＝3，

根据题意，得，

∵x＞0，

∴，，

∴，

∴x2+4＝3x，

∴x2﹣3x+4＝0，

∴△＝b2﹣4ac＝﹣7＜0，

∴方程x2﹣3x+4＝0没有实数根，

∴该函数的图象上不存在点C，使d（O，C）＝3．

（3）设D（x，y），

根据题意得，d（O，D）＝|x﹣0|+|x2﹣5x+7﹣0|＝|x|+|x2﹣5x+7|，

∵，

又x≥0，

∴d（O，D）＝|x|+|x2﹣5x+7|＝x+x2﹣5x+7＝x2﹣4x+7＝（x﹣2）2+3，

∴当x＝2时，d（O，D）有最小值3，此时点D的坐标是（2，1）．

（4）如图，以M为原点，MN所在的直线为x轴建立平面直角坐标系xOy，将函数y＝﹣x的图象沿y轴正方向平移，直到与景观湖边界所在曲线有交点时停止，

设交点为E，过点E作EH⊥MN，垂足为H，修建方案是：先沿MN方向修建到H处，再沿HE方向修建到E处．

理由：设过点E的直线l1与x轴相交于点F．在景观湖边界所在曲线上任取一点P，过点P作直

线l2∥l1，l2与x轴相交于点G．

∵∠EFH＝45°，

∴EH＝HF，d（O，E）＝OH+EH＝OF，

同理d（O，P）＝OG，

∵OG≥OF，

∴d（O，P）≥d（O，E），

∴上述方案修建的道路最短．

24．解：由点A（0，2），B（1，0），C（﹣4，0）可知：OA＝2，OC＝4，OB＝1，

在直角三角形AOC和直角三角形AOB中，根据勾股定理可求：AC＝＝2，

AB＝＝．

（1）在直角三角形AOC和直角三角形AOB中，tan∠ACO＝＝，tan∠BAO＝＝，所以∠ACO ＝∠BAO，

∵∠ACO+∠CAO＝90°，

∴∠BAO+∠CAO＝90°，∠BAC＝90°，

∴△ABC是直角三角形．

（2）①由（1）知：∠BAC＝90°，∴BD是圆M的直径，

∵DE是圆M的切线，∴∠BDE＝90°．

∴∠CDE+∠ADB＝90°，又∠ADB+∠ABD＝90°，∴∠CDE＝∠ABD，

∵∠DCE+∠ABO＝90°，∠ABO+∠BAF＝90°，∴∠DCE＝∠BAF

∴△CDE∽△ABF．

②当四边形ABND为矩形时，∵∠ABN＝90°，∴AN是圆的直径，由OB是直角三角形ABN的斜边上

的高线，由∠BAO＝∠BA0，∠BOA＝∠ABN＝90°，

∴△AOB∽△ABN，

∴＝，

∴AB2＝OA×AN，

∵OA＝2，AB＝，可求：AN＝，

∴ON＝，OM＝MN﹣ON＝，

在直角三角形OBM中，

tan∠DBC＝＝．

（3）若点D在线段AC上，

如图2：由①知△CDE∽△ABF可得：，AC＝2，

由＝，可得：CD＝，AD＝，

在直角三角形ABD中，由勾股定理可求：BD＝＝，

∵∠CBD＝∠FBO，∠BOF＝∠BDE＝90°，

∴△BFO∽△BED，

∴，

设：DE＝2x，则BF＝3x，由勾股定理得：OF＝＝，

∴，解得：x＝，

∴DE＝，BF＝，DF＝BD﹣BF＝，

∴＝，

若点D在线段AC的延长线上，

如图3：∵DE是圆M的切线，

∴∠BDE＝90°

∴∠EDC+∠CDB＝90°

∵∠ABD+∠CDB＝90°

∴∠EDC＝∠ABD，

∵∠DEB+∠DBE＝90°，∠DBE+∠OFB＝90°

∴∠DEB＝∠OFB，

∴△CDE∽△ABF，可得：，AC＝2，

由＝，可得：CD＝，∴AD＝AC+CD＝，由勾股定理得：BD＝＝，

∵∠CBD＝∠FBO，∠BOF＝∠BDE＝90°，

∴△BFO∽△BED，

∴，

设：DE＝2x，则BF＝3x，

由勾股定理得：OF＝＝，

∴＝，

解得：x＝，

∴DE＝2x＝，BF＝3x＝，DF＝BD﹣BF＝，∴＝．

综上所述：的值是或．

图3