大学模糊数学试题
模糊数学试题07

东北大学考试试卷(A B 卷) 2007 — 2008学年 第2学期课程名称:模糊数学┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 2分 共计10分) 1. 设论域12345{,,,,}U u u u u u =,F 模糊集(0.5,0.1,0,1,0.8)A =,(0.1,0.4,0.9,0.7,0.2)B =,(0.8,0.2,1,0.4,0.3)C =。
则_________A B ⋃=___________A B ⋂= ()____________A B C ⋃⋂=_________c A = 2. 设论 域{,,,,}U a b c d e =, 有{}0.70.8{,}0.50.7{,,}0.30.5{,,,}0.10.3{,,,,}00.1d c d A c d e b c d e a b c d e λλλλλλ<≤⎧⎪<≤⎪⎪=<≤⎨⎪<≤⎪≤≤⎪⎩ F 集A =_________________ 二、 计算题(共5小题,每题12分) 1. 设[0,10]U =为论域,对[0,1]λ∈,若F 集A 的λ截集分别为 [0,10]0[3,10]00.6[5,10]0.61[5,10]1A λλλλλλ=⎧⎪<≤⎪=⎨<<⎪⎪=⎩,求出:(1)(),[0,10]A x x ∈;(2)SuppA ;(3)KerA2. 设F 集112340.20.40.50.1A x x x x =+++,212340.20.50.30.1A x x x x =+++,312340.20.30.40.1A x x x x =+++, 12340.60.30.1B x x x =++,21230.20.30.5B x x x =++,试用格贴近度判断12,i B B A 与哪个最接近。
3.设120.100.80.70.20.40.90.50,0.30.10.600.40.310.50.2R R ⎛⎫⎛⎫ ⎪ ⎪== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭,求12121,,cR R R R R ⋃⋂4.设12345{,,,,}U u u u u u =,在U 上存在F 关系,使10.800.10.20.810.400.900.41000.10010.50.20.900.51R ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦,求ˆR,并由此进行聚类分析,画出聚类分析图。
模糊数学试题

华南理工大学研究生课程考试《 模糊数学 》样卷注意事项:1. 所有答案请按要求填写在答题纸上; 2. 课程代码:(S0003006)3.考试形式:闭卷( √ ) 开卷( ) 开闭卷结合( ) 4. 考试类别:博士研究生(√ ) 硕士研究生(√ )5. 试卷共 十二大题,满分100分,考试时间150分钟。
一、填空题1.设论域U={u 1,u 2,u 3,u 4,u 5},F 集A=(0.5,0.1,0,1,0.8), B=(0.1,0.4,0.9,0.7,0.2),则(A ⋃B)C =_______________。
2.设论域R=[0,3],且01112(),()213323xx x x A x B x x x x x ≤≤-≤≤⎧⎧==⎨⎨-<≤-<≤⎩⎩ 则它们的黎曼贴近度N(A,B)=_______________________。
3.0.410.70.510.62,323=_______123234=++=++⨯设,则。
4. 设A =[3,9], B =[7,10],则A +B = ,A ⨯B = 。
5.设论域U={1,2,…,10},且 0.20.40.60.811110.80.60.40.2[],[]4567891012345=++++++=++++大小 则[不大也不小]=_____________________________。
二、判断题(请在每小题的括号内认为正确的打“√”错误的打“⨯”) 1.λ≤μ ⇒ A λ ⊇A μ ( )2(A λ)c =(A c )λ ( ) 3 若A ⊆ B ⊆ C , 则N (A ,C ) ≤ N (A ,B )∨N (B ,C ) ( ) 4 若R 1⊆S 1, R 2⊆S 2,则 R 1∪R 2 ⊆ S 1∪S 2 ( ) 5 R∪R c = E ( )三、简答题(10分)1. 请写出隶属度函数的确定有哪几种方法。
2. 比较普通集合与模糊集合的异同。
模糊数学练习题
2.设“年老”的隶属函数为:
0 B ( x) 1 5 2 1 ( ) x 50 0 x 50
50 x 100
1)作出隶属函数曲线; 2)求 A B, A B, A, B 的隶属函数 ; 3)对x=30,40,45,分别求出对上述模糊集合 的隶属度;
A a1 a2 a3 A X B 0.1 0.4 0.7 b1 b2 b3 B Y CZ
0.9 0.6 0.3 C c1 c2 c3
1)求“若x为A且y为B,则z为C”的模糊关系矩阵; 2)若 A 1 0.4 1 , B 0.7 0.4 0.1 ,求 C ;
a1 a2 a3 b1 b2 b3
8.试写出下列模糊规则的关系矩阵表达式: 1)如果x为A或者B,则y为C; 2)如果x为A且B,则y为C; 3)如果x为A且y为B,则z为C或D;
3.设模糊集合为:
A 0.2 0 0.1 0.6 1 0.4 0.8 a b c d e f g
求截集 A0.3 , A0.5 , A0.8 及A的支集;
4.设X={0,1,2,3,4,5},Y={0,1,2,…,25} 有映射f:X→Y,f(x)=x2, 对于X上的两个模糊集合:
1 1 0.9 0.7 0.3 A 0 1 2 3 4 0.2 0.5 0.8 1 B 2 3 4 5
求f(A),f(B);
5.已知模糊关系矩阵
0.5 1 0 R1 0.5 1 0 0.5 0 1 0.5 0 1 R2 0 1 0.5 1 0.5 0
求 R1 R2 , R1 R2 , R1 R2 , R1 R2 , R2 R1 ;
东北大学模糊数学试题

东北大学考试试卷(A B 卷) 2007 — 2008学年 第2学期课程名称:模糊数学┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 2分 共计10分) 12345{,,,,}U u u u u u =,F 模糊集(0.5,0.1,0,1,0.8)A =,(0.1,0.4,0.9,0.7,0.2)B =,(0.8,0.2,1,0.4,0.3)C =。
则_________A B ⋃=___________A B ⋂=()____________A B C ⋃⋂=_________c A =2. 设论 域{,,,,}U a b c d e =,有{}0.70.8{,}0.50.7{,,}0.30.5{,,,}0.10.3{,,,,}00.1d c d A c d e b c d e a b c d e λλλλλλ<≤⎧⎪<≤⎪⎪=<≤⎨⎪<≤⎪≤≤⎪⎩F 集A =_________________5小题,每题12分) 设[0,10]U =为论域,对[0,1]λ∈,若F 集A 的λ截集分别为 [0,10]0[3,10]00.6[5,10]0.61[5,10]1A λλλλλλ=⎧⎪<≤⎪=⎨<<⎪⎪=⎩,求出:(1)(),[0,10]A x x ∈;(2)SuppA ;(3)KerA 2. 设F 集112340.20.40.50.1A x x x x =+++,212340.20.50.30.1A x x x x =+++,312340.20.30.40.1A x x x x =+++, 12340.60.30.1B x x x =++,21230.20.30.5B x x x =++,试用格贴近度判断12,i B B A 与哪个最接近。
3.设120.100.80.70.20.40.90.50,0.30.10.600.40.310.50.2R R ⎛⎫⎛⎫ ⎪ ⎪== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭,求12121,,cR R R R R ⋃⋂4.设12345{,,,,}U u u u u u =,在U 上存在F 关系,使10.800.10.20.810.400.900.41000.10010.50.20.900.51R ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦,求ˆR,并由此进行聚类分析,画出聚类分析图。
模糊数学试题(B)

南京工业大学 模糊数学与控制 试题(B )卷(闭)2009— 20010学年 第一学期 使用班级信科0701班级 ______________ 学号_____________ 姓名 _____________________ 题号-一--二二三四五六七总分得分一填空题(共36分)1处理现实对象的数学模型可分为三大类: ________________ , __________ , ____________ 。
2 设论域 U -^u 1,u 2,u 3,u 4,u^, F 集A =0.3 0.7 1 0.5, F 集U iU 2U 3U 53 设论域 U = 0,2 , A(U )二 U ,则(A A )=(A A C ) = ___________________________N(A,B)二 __________ 。
26设R,R 2都是实数域上的F 关系,R(x, y)=e*T ), R 2(X , y)=e"T ),则(R 1 R 2)C (3,2) = ________________ ,(R 1CR 2C )(3,2) = _________________ 。
7 设论域 ^'U 1,U 2,U ^ , V J v 1,V 2,V 3,V 4? , R F(U V),且t ,, t1亠0.3 0.6 0.0, 1 亠 5设论域 U = U 1,U 2,U 3,U 4,U 5・,F集A 二+ +++, F 集U1U 2 U 3U4 U 5m 0.1 0.8 0.4 0.7B,则 AB-------------------------------------5A0B =,格贴近度4设U 为无限论域,F 集A 二 x,则截集A 1 =e,A 二oU 1 U 3 U 4 U 5「匹些空卩则A B 二U 1 U 2 U 4 U 5,A B = _________________f (x, y, z) _ a i ,此时函数f (x, y, z)的表达式为二(12分)设U=0,5,对… 0,1丨,若F 集A 的■截集分别为 A,二 fij求出:(1)隶属函数 A(x) ; (2) SuppA ;(3) KerA 。
模糊数学考试习题

模糊数学考试习题第一篇:模糊数学考试习题一、填空(每空3分)1.经典集合是论域U到集合的映射.2.模糊集合是论域U到集合的映射.3.经典集合的关系矩阵是.4.模糊集合的模糊关系矩阵是.5.模糊的不确定性即使时间过去了(或者实际作了一次试验)仍然是6.模糊数学把数学的应用范围从精确现象扩大到领域.7.模糊矩阵运算关于交的分配律.8.模糊集的隶属函数是专家给出的.9.模糊集强调的是集合边界的定义.10.模糊聚类方法给出的分类结果不是说事物绝对的属于或绝对的不属于类.11.集合U、V的直积U⨯V的子集R称为U到V的关系.12.U⨯V的一个模糊子集R称为U到V的关系.~13.经典集合的值域是.14.模糊集合的值域是.15.经典集合YI c的排中(互补)律.16.模糊集合YI c的排中(互补)律.17.模糊集的隶属函数是存在.18.模糊聚类方法给出的分类结果.19.模糊模式识别的最大隶属原则有个.20.模糊集的λ截集将模糊集的隶属函数转化为普通集合的二、简述题(每小题15分)1.简述模糊集的一种表示方法,并进行说明.2.简述模糊聚类的编网法.3.写出三种模糊分布函数.4.简述模糊集的一种运算,并进行说明.5.简述模糊聚类的最大树法.6.简述分解定理与扩张原理。
三、举一应用模糊数学方法解决实际问题的例子(25分)第二篇:数学考试一、聪明的你来填一填:(每空0.5分,共12分)1.在()里填上合适的单位:一块玻璃的厚度大约是3()骑自行车每小时行驶15()李明体重35()一辆汽车载重5()2、在()里填上合适的数:5厘米=()毫米2千米=()米()米=50分米4000千克=()吨6千克=()克8吨=()千克1600千克-600千克=()吨14厘米 + 26厘米 =()分米3、在○里填上“>、<或=”:70厘米○90毫米5千米○4500米990克○1千克1500千克○2吨4、把序号填在下面的括号内:5、括号里最大能填几?()×6<498×()<63()×5<446、用0、1、2组成最大的三位数是(),最小的三位数是(),他们的差是()。
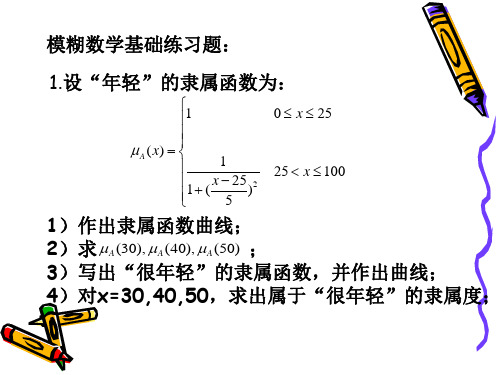
模糊数学基础练习题

模糊数学基础练习题模糊数学基础练习题在现代数学中,模糊数学是一门研究不确定性和模糊性的数学分支。
它通过引入模糊集合和模糊逻辑,为处理现实世界中模糊和不确定的问题提供了一种有效的工具。
为了更好地理解和应用模糊数学,下面将给出一些模糊数学基础练习题。
1. 模糊集合:给定一个模糊集合A = {(x, μA(x))},其中x是集合的元素,μA(x)是元素x的隶属度。
请计算集合A的支持度和核。
2. 模糊逻辑运算:假设有两个模糊集合A = {(x, μA(x))}和B = {(x, μB(x))},请计算它们的模糊交、模糊并和模糊补运算。
3. 模糊关系:考虑一个模糊关系R = {(x, y, μR(x, y))},其中x和y是集合的元素,μR(x, y)是元素x和y之间的关系强度。
请计算关系R的模糊合成和模糊反关系。
4. 模糊推理:假设有一个模糊规则库,包含多个模糊规则,如“If x is A and y is B, then z is C”,其中A、B和C分别是模糊集合。
请利用模糊推理方法,根据给定的输入模糊集合,推导出输出模糊集合。
通过解答以上练习题,我们可以更好地理解和应用模糊数学。
模糊数学的应用领域广泛,包括模糊控制、模糊决策、模糊优化等。
它在处理不确定性和模糊性问题时具有很强的适应性和灵活性,能够更好地反映现实世界中的复杂性和模糊性。
总之,模糊数学是一门重要的数学分支,它为处理现实世界中模糊和不确定的问题提供了一种有效的工具。
通过不断练习和应用,我们能够更好地掌握模糊数学的基础知识和技巧,为解决实际问题提供更准确和可靠的方法。
模糊数学考试题

模糊数学考试题一、选择题(每题1分,共30分)1. 模糊集合最早由哪位数学家引入?A. George KlirB. Lotfi ZadehC. Zadeh LotfiD. George Boole2. 模糊逻辑的基本操作是?A. 与、或、非B. 加、减、乘、除C. 并、交、差D. 集合的包含与被包含3. 模糊集合的隶属函数的取值范围是?A. [0,1]B. [0,∞)C. (0,1)D. (0,∞)4. 以下哪个是模糊推理的方法?A. BP神经网络B. 遗传算法C. 最大似然估计D. 模糊推理算法5. 模糊数学最初的应用领域是?A. 人工智能B. 控制理论C. 图像处理D. 统计学...二、填空题(每题2分,共20分)1. 模糊数学是基于()集合理论的一种数学理论。
2. 模糊逻辑中,非真即()。
3. 模糊集合的隶属函数可用()函数来表示。
4. 模糊数学中,我们用模糊关系来描述()。
5. 模糊数学最重要的应用之一是在()理论中。
...三、问题解答题(每题15分,共60分)1. 简述模糊集合的定义和特点。
模糊集合是指在给定的范围内,每个元素都具有一定的隶属度,是介于完全属于和完全不属于之间的中间状态。
模糊集合的隶属度用隶属函数表示。
与传统集合不同,模糊集合的元素可以部分属于集合,这种模糊边界的概念反映了现实世界中存在的不确定性和模糊性。
2. 简述模糊逻辑的基本原理。
模糊逻辑是基于模糊集合理论的一种逻辑系统。
它以真值不再是二值(0或1)为基础,而是用模糊集合的隶属度来表示概率。
模糊逻辑中,逻辑运算包括模糊与、模糊或、模糊非等。
与传统逻辑相比,模糊逻辑更能应对真实世界中存在的不确定性和模糊性。
3. 简述模糊推理的基本方法。
模糊推理是根据给定的模糊规则和事实,通过运用模糊逻辑的方法进行推理推断。
模糊推理的基本方法包括模糊匹配、模糊推理和模糊控制。
其中,模糊匹配是将模糊规则中的条件与已知事实进行匹配;模糊推理是根据匹配的程度和隶属度进行推理;模糊控制是将推理的结果转化为对系统的控制动作。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
⎪⎪⎭
⎫
⎝⎛3.05.08.01.0⎪⎪⎭
⎫
⎝⎛5.05.08.05.0大学模糊数学期末试题
命题人:控制与计算机工程学院 测控技术与仪器 测控1003班 吴国勋 1101160319
一、 选择题(共2小题,每题5分,共10分) 1、设集合A={1,2,3,4,5,6},f 是如下定义的:
f:x ∈A →f(x)=6/x ∈A.则f 的定义域( ) A 、(1,2,3,6) B 、(1,2,5,6) C 、(2,3,4,6) A 、(1,3,4,6) 2、设A= 则t(A)=( )
A
⎪⎪⎭
⎫ ⎝⎛2.05.08.05.0 B ⎪⎪⎭
⎫ ⎝⎛5.08.08.05.0 C ⎪⎪⎭
⎫
⎝⎛5.02.08.05.0 D
二、 填空题(共5小题,每空2分,共20分) 1、已知下列各集合
A={y|y=2x+1,x>0},B={y|y=-3x+9} 则A ∩B=_______;A ∪B=_________. 2、(A ∩B )∪C=(A ∪C)________(B ∪C). 3、设},,,,{54321u u u u u U =,)
8.0,1.0,3.0,4.0,7.0(~
=A ,)6.0,5.0,1.0,9.0,2.0(~
=B ,
则
=c A ~
,~
A
=c B ~。
4、若模糊概念a 在论域U 上的模糊集为~
A ,则判断句“u 是a ”的真值为 。
5、模糊矩阵R=n
n ij
r
⨯)(如果满足自反性 ,对称
性 ,传递性 , 就称R 是一个 。
三、 判断题(共5小题,每题2分,共10分)
10
1
918178.066.054.042.0++++++5
2.044.036.028.011++++1、λ)(C
A 和C A )(λ是相等的。
( )
2、设A,B 是模糊对称矩阵,则A ∪B,A ∩B ,A 。
B 都是模糊对称矩阵。
( )
3、设A,B 是模糊自反矩阵,则A ∪B,A ∩B, A 。
B 都是模糊自反矩阵。
( )
4、设a=(a1,a2,…,an ),b=(b1,b2,…,bn)。
则b a b a ∧≤∙。
( )
5、在实数里关系f={(x,2x)}是对称的、自反的。
( ) 四、 计算题(共4小题,每题10分,共40分) 1、论域U={1,2,3,···,10},定义 “大”=A= “小
”=B=
试求C=“不大”,D=“不小”,E=“或大或小”,F=“不大也不小”。
2
、
设
论
域
X={x1,x2,x3,x4,x5},
模
糊
集
合
A=(0.4,0.1,0.5,0.3,0.6),B=(0.4,0.5,0.9,0.5,1),计算(A ∪B)∩C,(A ∩B)∪C. 3、解方程
⎪⎪⎪⎪⎪⎭⎫ ⎝⎛2.01.07.08.04.04.05.02.0。
⎪⎪⎭⎫ ⎝⎛21x x =⎪⎪⎪⎪⎪⎭⎫ ⎝⎛2.06.04.05.0
4、设论域},,,,{54321u u u u u U
=由父、子、女、邻居、母五人组成,
请陌生人对这五人按相貌相象程度进行模糊分类,并画出动态聚类图。
已知相似矩阵为
R=⎥⎥⎥⎥⎥⎥⎦
⎤
⎢⎢⎢⎢⎢⎢⎣⎡11
.09
.085
.02
.01.0102.01.09.0018.06.085
.02.08.018.02.01.06.08.01
五、 讨论题(共3小题,共20分)
1、 举出一个模糊数学的实例,并写出相应的模糊矩阵。
(6分)
2、 说明模糊性和偶然性的区别。
(6分)
3、 叙述动态聚类分析的解题步骤。
(8分)。
