Ica盲源分离Matlab程序
matlab语音信号盲分离

目录摘要 0abstract (1)1 ICA 的基本原理及特点 (2)1.1盲分离数学模型 (2)1.2 ICA 算法描述 (3)1.3 FICA算法 (4)2 FICA设计思想 (4)3 实验仿真结果记录 (6)3.1 仿真时域波形及频谱 (6)3.1.1 原始信号 (6)3.1.2 混合信号 (9)3.1.3 分离信号 (12)3.2 仿真所用的源程序 (15)4 实验结果分析 (24)5 小结与体会 (25)6 参考文献 (26)摘要混合信号中恢复出未知源信号。
语音信号盲分离技术被成功地用在了通信、医学、图像和语音信号处理等领域。
我们所要研究的混合语音信号盲分离问题就是用麦克风阵列或多个麦克风阵列来模仿人的耳朵,采集得到相互干扰的混叠语音信号,然后通过分离算法将混叠的语音信号相互分离开来,提取我们所感兴趣的信号。
举个例子就是在多人同时说话的嘈杂环境下,我们能够辨识感兴趣人的说话声的能力。
然后把它分辨出来。
abstractThe speech signal blind source is in the source signal and the source signal how to mix all unknown, from observations of mixed signal in recovering the unknown sourcecommunication, medical, image and voice signal processing, etc. We have to study mix of speech signal is blind source separation with a microphone array or more microphone array to imitate human ears, acquisition get each other interference aliasing speech signal, and then through the separation algorithm will aliasing voice signal mutual separated, extraction we are interested in signal. For example is more than in noisy environment of speak at the same time, we can identify interested in the ability of the human voice. And then take it apart.1 ICA 的基本原理及特点1.1 盲分离数学模型盲信号分离是指在没有任何先验知识的条件下,仅根据源信号之间的统计独立特性和由传感器输出的观测信号,把源信号分离出来。
盲源分离matlab

盲源分离matlab【最新版】目录1.盲源分离的概念2.MATLAB 在盲源分离中的应用3.盲源分离的步骤和方法4.盲源分离的实例与结果分析5.盲源分离的优缺点及发展前景正文1.盲源分离的概念盲源分离(Blind Source Separation,简称 BSS)是一种信号处理技术,其目的是从观测到的混合信号中分离出相互独立的原始信号。
这些原始信号通常是未知的,且可能具有不同的统计特性。
盲源分离在许多领域都有应用,如通信、语音处理、生物医学信号处理等。
2.MATLAB 在盲源分离中的应用MATLAB 是一种广泛使用的数学软件,它提供了丰富的函数库和强大的计算能力,使得盲源分离算法的实现变得简便。
在盲源分离领域,MATLAB 可以用于信号模拟、算法设计和结果分析等。
通过 MATLAB,研究者可以轻松地尝试不同的分离算法,并对比其性能,从而为实际应用提供有力支持。
3.盲源分离的步骤和方法盲源分离的过程主要包括以下几个步骤:(1)信号模型建立:根据问题的实际情况,建立混合信号的数学模型,如线性混合模型、非线性混合模型等。
(2)统计特性分析:分析原始信号的统计特性,如均值、方差、相关性等,为后续算法设计提供依据。
(3)分离算法选择:根据信号模型和统计特性,选择合适的盲源分离算法,如独立成分分析(ICA)、广义逆滤波(GIV)、非负矩阵分解(NMF)等。
(4)算法实现与性能评估:利用 MATLAB 实现选定的分离算法,并通过仿真实验评估其性能。
4.盲源分离的实例与结果分析以下是一个简单的盲源分离实例:假设有两个原始信号 x1(t) 和 x2(t),它们通过线性混合器后得到观测信号 y(t):y(t) = x1(t) + x2(t)通过盲源分离,我们可以从 y(t) 中恢复出 x1(t) 和 x2(t)。
利用 MATLAB,我们可以实现以下步骤:(1)生成两个原始信号 x1(t) 和 x2(t),它们具有不同的统计特性。
复数信号盲源分离matlab

复数信号盲源分离matlab摘要:1.引言2.复数信号盲源分离原理3.MATLAB实现方法4.仿真结果及分析5.结论正文:【引言】随着科技的发展,信号处理技术在各个领域得到了广泛的应用。
在实际应用中,常常遇到复数信号的盲源分离问题。
复数信号盲源分离是指在未知信号源的幅度、相位和频率等信息的情况下,仅通过观测到的复数信号来实现信号的分离。
MATLAB作为一种强大的数学软件,可以方便地实现复数信号的盲源分离。
本文将介绍复数信号盲源分离的MATLAB实现方法及仿真结果。
【复数信号盲源分离原理】复数信号盲源分离的核心是利用信号之间的相互关系和某种优化算法来达到分离目的。
常见的盲源分离算法有:独立成分分析(ICA)、非线性独立成分分析(NICA)、联合diagonalization(JADE)等。
这些算法在实数信号盲源分离领域取得了较好的效果,对于复数信号盲源分离,可以通过对实部与虚部进行独立成分分析来实现。
【MATLAB实现方法】在MATLAB中,可以使用现成的盲源分离工具箱(如BSSbox)来实现复数信号的盲源分离。
以下是一个简单的MATLAB实现步骤:1.导入所需库:如bssbox、plot等。
2.读取或生成复数信号数据。
3.对复数信号进行预处理,如白化、窗函数处理等。
4.选择合适的盲源分离算法,如ICA、NICA、JADE等。
5.使用盲源分离算法对预处理后的信号进行分离。
6.绘制分离后的信号,分析分离效果。
【仿真结果及分析】通过MATLAB仿真,可以得到复数信号盲源分离的结果。
分离效果可以通过比较分离后的信号与原始信号的相似度来评价。
在实际应用中,可以根据需求选择合适的分离算法和参数,以达到较好的分离效果。
【结论】本文介绍了复数信号盲源分离的MATLAB实现方法。
通过使用盲源分离工具箱和选择合适的算法,可以有效地实现复数信号的盲源分离。
仿真结果表明,所选算法在复数信号盲源分离问题上具有一定的可行性。
matlab 盲源分离 jade算法

Matlab 盲源分离 JADE 算法一、引言盲源分离是信号处理中的一个关键问题,用于从混合信号中分离出各个独立的源信号。
在实际生活中,混合信号往往是通过各种传感器或者设备采集得到的,源信号可能是声音、图像等各种形式的信息。
而盲源分离的任务就是从这些混合信号中还原出源信号,为后续的分析和处理提供基础。
JADE(Joint Approximate Diagonalization of Eigenmatrices)算法是一种经典的盲源分离算法,本文将介绍如何使用Matlab实现JADE算法,并探讨其在实际应用中的效果。
二、JADE算法的原理JADE算法是一种高阶统计方法,主要用于盲源分离和独立成分分析。
其基本思想是通过对数据的高阶统计特性进行分析,从而实现对独立源信号的估计和分离。
具体来说,JADE算法利用了信号的高阶统计独立性来实现盲源分离,通过对数据进行协方差矩阵的估计和特征值分解,进而得到信号的独立成分。
三、Matlab实现JADE算法的步骤使用Matlab实现JADE算法通常包括以下几个步骤:1. 数据准备:首先需要准备混合信号的数据,可以是从传感器采集得到的音频数据、图像数据等各种形式的信号数据。
2. 数据预处理:对采集到的数据进行预处理,包括降噪、滤波、归一化等操作,以保证数据的质量和稳定性。
3. JADE算法实现:利用Matlab提供的相关函数或者自行编写代码,实现JADE算法的核心步骤,包括协方差矩阵的估计、特征值分解等。
4. 结果分析:对JADE算法得到的分离后的独立成分进行分析和评估,包括信噪比的计算、频谱分析等。
四、JADE算法在实际应用中的效果JADE算法作为一种经典的盲源分离方法,在实际应用中取得了广泛的应用。
以语音信号分离为例,利用JADE算法可以将混合的多个说话人的语音信号分离成独立的单一说话人的语音信号,为语音识别、语音合成等应用提供了重要的基础。
另外,在无线通信、生物医学信号处理等领域,JADE算法也发挥了重要作用。
ICA快速算法原理和matlab算法程序

顿迭代法解方程(3.8) 。用 F 表示式(3.8)左边的函数,可得 F 的雅可比矩阵 JF W 如 下:
JF W E XX T g ' W T X I
(2.9)
为了简化矩阵的求逆,可以近似为(3.9)式的第一项。由于数据被球化, E XX T I , 所 以,E XX T g ' W T X
Y=WP'*Z; G=Y.^3;%G为非线性函数,可取y^3等 GG=3*Y.^2; %G的导数 count=0; LastWP=zeros(m,1); W(:,n)=W(:,n)/norm(W(:,n)); while abs(WP-LastWP)&abs(WP+LastWP)>Critical count=count+1; %迭代次数 LastWP=WP; %上次迭代的值 % WP=1/T*Z*((LastWP'*Z).^3)'-3*LastWP; for i=1:m WP(i)=mean(Z(i,:).*(tanh((LastWP)'*Z)))-(mean(1-(tanh((
(2.10)
这里, W 是 W 的新值, E W T Xg W T X ,规格化能提高解的稳定性。简化后就可 以得到 FastICA 算法的迭代公式:
W E Xg W T X E g ' W T X W W W / W
T
T
I ,其中: I 为单位矩阵,我
T
们称这个向量为白化向量。白化的本质在于去相关,这同主分量分析的目标是一样的。在 ICA 中 , 对 于 为 零 均 值 的 独 立 源 信 号 S t S1 t ,..., S N t , 有 :
Matlab中的盲源信号分离方法与示例分析

Matlab中的盲源信号分离方法与示例分析引言:随着科学技术的发展,信号处理在各个领域中扮演着重要的角色。
其中,盲源信号分离(Blind Source Separation,BSS)作为一种重要的信号处理方法,用于从混合信号中恢复出原始信号的成分,已经在音频处理、图像处理、生物医学工程等多个领域得到了广泛的应用。
在本文中,将介绍Matlab中的盲源信号分离方法以及相关示例分析。
一、盲源信号分离方法介绍1.1 独立成分分析(Independent Component Analysis,ICA)独立成分分析是一种基于统计原理的盲源信号分离方法。
其核心思想是假设混合信号是通过独立的源信号进行线性叠加得到的。
通过对混合信号的统计特性进行分析,可以估计出源信号的独立成分,从而实现信号的分离。
1.2 因子分析(Factor Analysis)因子分析是一种基于概率模型的盲源信号分离方法。
它假设混合信号是通过一组共享的隐变量与线性映射关系得到的。
通过对混合信号的协方差矩阵进行分解和对隐变量的估计,可以恢复出源信号的成分。
1.3 主成分分析(Principal Component Analysis,PCA)主成分分析是一种常见的线性降维方法,也可以用于盲源信号分离。
其基本思想是通过找到数据中最大方差的方向,将原始数据映射到一个低维的子空间中,从而实现信号分离。
二、示例分析2.1 音频信号的分离在音频处理中,盲源信号分离方法可以用于提取出不同的音频源,例如乐器音轨、人声等。
下面以一个示例进行分析。
首先,我们随机选择两段音频,分别为X1和X2,并将它们混合产生一个混合音频Y。
然后,利用盲源信号分离方法对Y进行处理,尝试将其恢复出X1和X2。
在Matlab中,可以使用FastICA工具箱实现独立成分分析。
具体步骤如下:(1)读取音频文件,并将音频信号转化为时间序列的形式。
(2)利用FastICA函数对混合音频Y进行处理,得到分离后的音频信号S。
单通道信号盲源分离代码

单通道信号盲源分离代码这是一个使用Python和sklearn库进行单通道信号盲源分离的简单示例。
假设我们有一些混合的信号,我们希望恢复原始的源信号。
在这个示例中,我们将使用FastICA算法进行盲源分离。
首先,你需要安装必要的库,如果还没有安装的话,可以使用以下命令进行安装:pythonpip install numpy scipy sklearn然后,你可以使用以下代码进行盲源分离:pythonimport numpy as npfrom sklearn.decomposition import FastICAimport matplotlib.pyplot as plt# 生成一些混合的信号np.random.seed(0)n_samples = 2000time = np.linspace(0, 8, n_samples)s1 = np.sin(2 * time) # Signal 1 : sinusoidal signals2 = np.sign(np.sin(3 * time)) # Signal 2 : square signals3 = signal.sawtooth(2* np.pi * time) # Signal 3: sawtooth signal S = np.c_[s1, s2, s3]S += 0.2 * np.random.normal(size=S.shape) # Add noiseS /= S.std(axis=0) # Standardize data# Mix dataA = np.array([[1, 1, 1], [0.5, 2, 1.0], [1.5, 1.0, 2.0]]) # MixingmatrixX = np.dot(S, A.T) # Generate observations# Compute ICAica = FastICA(n_components=3)S_ = ica.fit_transform(X) # Reconstruct signals# We can `prove` that the ICA model applies by reverting the unmixing.assert np.allclose(S, np.dot(S_, ica.mixing_.T) + ica.mean_) # For comparison, compute PCA (e.g. for denoising)from sklearn.decomposition import PCApca = PCA(n_components=3)H = pca.fit_transform(X) # Reconstruct signals based on orthogonalcomponents# Plot resultsplt.figure()colors = ['navy', 'turquoise', 'darkorange']for ii, (s, (ica_s, pca_s)) in enumerate(zip(S_.T, H.T)):plt.plot(time, s, color=colors[ii], label='True signal')plt.plot(time, ica_s, color=colors[ii], label='ICA recovered signal')plt.plot(time, pca_s, color=colors[ii], label='PCA recovered signal')plt.legend()plt.show()这段代码首先生成了三个不同的信号(正弦波、方波和锯齿波),然后将它们混合在一起。
ICA快速工具包使用说明文档
说明文档
ICALAB使用说明:
1、打开matlab,在command window 窗口输入icalab 调用盲源分离程序工具箱
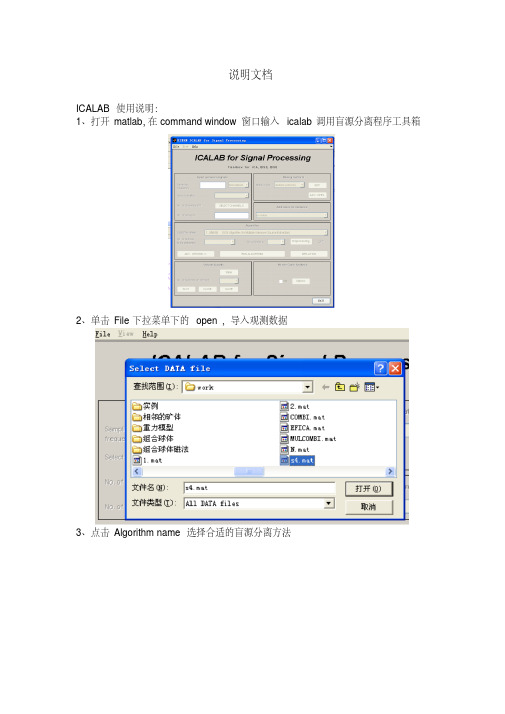
2、单击File下拉菜单下的open ,导入观测数据
3、点击Algorithm name 选择合适的盲源分离方法
4、点击按钮,开始计算
5、点击View按钮选择要显示的信号
选择图中所示的信号,点击ok 然后点击PLOT按钮
6、点击PLOT后显示窗口如下依次为观测信号、分离信号、混合矩阵
7、打开Estimated matrix A中的Edit菜单,选择参数设置,双击图片,然后点击
Inspector按钮弹出参数设置对话框。
8、点击弹出Cdata参数,并记录下其
系数
9、点击SAVE按钮,弹出下面的对话框,保存数据
10、点击EXIT按钮,退出工具箱
11、在matlab中导入刚才保存的数据S为观测信号,Y为分离结果
12、用Y乘以步骤9中记录下来的数据,分别得到各条测线上的各个异常
s1(1,:)=Y(1,:)*CData(1,1); s1(2,:)=Y(2,:)*CData(1,2);
s2(1,:)=Y(1,:)*CData(2,1); s2(2,:)=Y(2,:)*CData(2,2);
其中,s1是第一条测线上两个异常分离结果,s2是第二条测线上两个异常分离结果。
