线性二自由度汽车模型的运动方程
线性二自由度汽车模型

α1 −α2 = KayL
m: vehicle mass
16/81
α1-α 2
K > 0不足转向
α1 −α2 = KayL
K = 0中性转向
ay
K < 0过度转向
a y > 0.3 ~ 0.4 g,α1 − α 2与a y不再为线性关系 α和ωr急剧变化,出现半径迅 速增加或减小的现象。 a y对α1 − α 2关系用斜率表示,斜率 > 0 ⇒ 不足转向
β
+
L1ω r
u
−δ
α2
= υ − L2ω r
u
= β − L2ω r
u
FY1 = k1α1 FY 2 = k2α2
6/81
⎩⎨⎧kL11αk11α+1
k2α2 = m(uωr + υ − L2k2α2 = I zωr
)
FY1 + FY 2 ≈ m(uωr+υ)
L1FY1 − L2FY 2 ≈ I zωr
13/81
ωr δ
⎟⎞ ⎠
K <0
K =0
K >0
ucr uch ua
14/81
W过度转向汽车车速达到临界车速时将失 去稳定性。因为只要一个很小的转角δ, 横摆角速度增益ωr/δ就趋于无穷大。
W因为假设纵向速度为优先值,根据纵向 速度与角速度的关系可知,汽车转向半 径极小。这样,汽车必定发生激转,导 致侧滑或侧翻的发生。
5.3 线性二自由度汽车模型 对前轮角输入的响应
1 线性二自由度汽车模型的运动微分方程
☆忽略转向系的影响,以前轮转角作为输入; ☆只在地面上做平面运动,忽略悬架作用; ☆前进(纵轴)速度不变,只有沿y轴的侧向速度 和绕z轴的横摆运动(ay<0.4g) ; ☆驱动力不大,对侧偏特性无影响; ☆忽略空气阻力; ☆忽略因载荷变化引起左、右轮胎特性的变化; ☆忽略回正力矩的变化。
汽车理论5.3

1 2 。
21
第三节 线性二自由度汽车模型对前轮角输入的响应
2)转向半径的比R/R0
已知 R R0 1 Ku 2
R 1 Ku 2 R0
K=0, R/R0=1,汽车具有中性转向特点; K>0, R/R0>1,汽车具有不足转向特点;
K<0, R/R0<1,汽车具有过多转向特点。
8
1 u
第三节 线性二自由度汽车模型对前轮角输入的响应
二、前轮角阶跃输入下汽车的稳态响应
—等速圆周行驶 1.稳态响应
稳态时ωr为定值
0 v
r 0
代入运动微分方程式得
v 1 k1 k2 ak1 bk2 r k1 mur u u v 1 2 ak1 bk2 a k1 b 2 k2 r ak1 0 u u
2
度的影响。
第三节 线性二自由度汽车模型对前轮角输入的响应
2.两轮汽车模型及车辆坐标系 y
x
3
第三节 线性二自由度汽车模型对前轮角输入的响应
3.运动学分析
确定汽车质心(绝
对)加速度在车辆坐标
系的分量ax和ay。
沿Ox轴速度分 量的变化为
u u cos u v vsin
(1)
(2)
由式(2)得
r I Z
1 2 a k1 b 2k2 r ak1 u ak1 bk2
28
第三节 线性二自由度汽车模型对前轮角输入的响应
求导后得
1 2 r a k1 b 2 k 2 r ak1 I Z u ak1 bk 2
汽车二自由度动力学模型

汽车二自由度动力学模型
汽车二自由度动力学模型是一种用于描述汽车运动的简化模型。
它考虑了两个自由度,通常是车辆的纵向(前进方向)和侧向(横向)运动。
在这个模型中,车辆被视为一个质量集中的刚体,通过两个自由度来描述其运动状态。
这两个自由度通常是车辆的速度(纵向)和横摆角速度(侧向)。
汽车二自由度动力学模型的建立基于一些基本的物理原理,如牛顿第二定律、动量守恒定律和刚体动力学。
通过对这些原理的应用,可以得到描述车辆运动的微分方程。
这些方程通常包括车辆的加速度、驱动力或制动力、转向力矩以及车辆的惯性参数等。
通过求解这些微分方程,可以预测车辆在不同工况下的运动响应,例如加速、制动、转弯等。
汽车二自由度动力学模型在车辆动力学研究、驾驶模拟器、自动驾驶系统等领域有广泛应用。
它可以帮助工程师和研究人员了解车辆的基本运动特性,评估车辆的操控稳定性、行驶安全性等方面的性能。
然而,需要注意的是,二自由度模型是一种简化的模型,它忽略了许多实际情况中的复杂因素,如悬挂系统、轮胎特性、空气动力学等。
在实际应用中,可能需要使用更复杂的多自由度模型或考虑更多的因素来更准确地描述汽车的运动。
总的来说,汽车二自由度动力学模型提供了一个简单而有用的工具,用于初步研究和理解汽车的运动行为,但在具体应用中,需要根据实际需求进行适当的修正和扩展。
如果你对汽车动力学模型有更深入的问题或需要进一步的讨论,我将很愿意提供帮助。
05-3 线性二自由度汽车模型

业 ¾ 输出、输入的幅值比是频率 f 的函数,称幅频特性。 工 ¾ 相位差也是 f 的函数,称为相频特性。
¾ 两者统称为频率特性。
车
汽
北
2010-5-20
共55页
17
第三节 线性二自由度汽车模型对前轮角输入的响应
权
版 ωr + 2ω0ζωr + ω02ωr = B1δ + B0δ
B0δ 0 ω02
= uL 1+ Ku2
δ0
=
ωr δ
⎞ ⎟
δ0
⎠s
工业 即稳态横摆角速度
ωr0
=
ωr δ
⎟⎞ ⎠s
δ
0
车对应的齐次方程为 汽ωr + 2ω0ζωr + ω02ωr = 0
北
2010-5-20
共55页
5
第三节 线性二自由度汽车模型对前轮角输入的响应
权
其通解可由如下特征方程求得
业 式中
工 ζ = h 2ω0m′
汽车 B1
=
b1 m′
ω02
=
c m′
ζ—阻尼比。
B0
=
b0 m′
北
2010-5-20
共55页
3
第三节 线性二自由度汽车模型对前轮角输入的响应
权
前轮角阶跃输入的数学表达式为
版
t < 0,δ = 0 ⎫
转 向
院 t
≥
0,δ
=
δ
0
⎪ ⎬
盘 转 角
学 t > 0,δ = 0 ⎪⎭
ω r = C e−ζω0tsin ω 0 1 − ζ 2 t + Φ
一种二自由度汽车运动微分方程的推导方法

《一种二自由度汽车运动微分方程的推导方法》
一、引言
二自由度汽车运动微分方程是汽车模式的基础,能够准确描述汽车的运动特性,是汽车控制中的重要参数。
本文通过对二自由度汽车运动的基本原理进行推导,探讨二自由度汽车运动微分方程的推导方法。
二、基本原理
二自由度汽车运动模型是汽车模型的基本框架,它考虑了汽车本身的动力学特性和运动轨迹的交互作用。
根据牛顿第二定律,汽车的运动状态可以用方程来描述,即汽车的运动微分方程。
三、推导方法
(1)在汽车运动模型中,首先根据牛顿第二定律推导出汽车的运动方程,即汽车的运动微分方程。
(2)然后,利用经典的Lagrange方程,可以求出汽车的质心速度和质心加速度,以及汽车的速度和角速度:
(3)最后,根据几何关系,可以求出汽车的位置和角度,从而得到汽车的运动微分方程。
四、结论
本文通过对二自由度汽车运动的基本原理进行推导,探讨了一种二自由度汽车运动微分方程的推导方法。
结果表明,在推导汽车运动微分方程时,需要充分考虑汽车的动力学特性、运动轨迹特性以及几何关系。
车辆二自由度模型状态空间方程

车辆二自由度模型状态空间方程一、车辆二自由度模型状态空间方程车辆二自由度模型是车辆动力学中常用的简化模型之一,它将车辆简化为一个在平面上运动的质点。
在这个模型中,车辆可以做平面上的平移和转动运动,因此被称为车辆的二自由度模型。
而状态空间方程则是描述这一模型运动规律的数学工具。
在车辆二自由度模型中,通常采用平移运动的位置和速度以及转动运动的姿态角和角速度作为描述车辆状态的变量。
通过对车辆动力学和控制理论的研究,可以得到描述车辆二自由度模型的状态空间方程。
这些方程包括车辆的位置、速度、姿态角和角速度之间的动态关系,可以用来描述车辆在不同行驶状态下的运动规律。
二、深度分析车辆二自由度模型状态空间方程车辆二自由度模型状态空间方程的深度分析需要从车辆动力学和控制理论的角度进行。
我们需要深入了解车辆的平移和转动运动规律,包括车辆在不同速度和转角条件下的运动特性,以及外部环境对车辆运动的影响。
我们需要探讨车辆控制系统对车辆状态的影响,包括如何通过控制输入来影响车辆的运动状态。
我们需要分析车辆二自由度模型状态空间方程的数学推导和物理意义,以深入理解车辆状态空间方程的结构和参数含义。
在具体的分析过程中,我们可以通过建立车辆运动的动力学模型和控制模型,使用数学工具进行模型分析和仿真验证,从而深入理解车辆二自由度模型状态空间方程的动态性质和稳定性。
三、撰写高质量车辆二自由度模型状态空间方程文章基于以上的深度分析,我们可以着手撰写一篇高质量的文章。
我们可以介绍车辆二自由度模型的基本原理和概念,然后逐步展开对车辆状态空间方程的分析和推导,包括车辆运动学和动力学的描述,以及状态空间方程的数学结构和物理意义。
在文章中,我们可以多次提及车辆二自由度模型状态空间方程的关键词,以加强文章的专业性和知识性。
我们还可以结合个人的观点和理解,对车辆二自由度模型状态空间方程进行综合性的总结和回顾,为读者提供全面、深刻和灵活的理解。
一篇关于车辆二自由度模型状态空间方程的高质量文章需要具备深度和广度兼具的分析能力,结合个人观点和实践经验,以及对读者的引导和启发。
汽车二自由度运动学模型

汽车二自由度运动学模型汽车是我们日常生活中常见的交通工具之一,而了解汽车的运动学模型是研究汽车运动的重要基础。
汽车的运动学模型可以简化为二自由度模型,即在平面上的前进方向和转向方向。
在汽车二自由度运动学模型中,我们假设汽车的前进方向和转向方向是独立的。
这意味着汽车可以同时进行前进和转向的运动。
前进方向是汽车沿着道路直线行驶的方向,而转向方向是指汽车绕垂直于道路的轴线旋转的方向。
在分析汽车的运动学模型时,我们需要考虑一些重要的参数和变量。
首先是汽车的速度,即汽车在前进方向上的运动速度。
其次是汽车的转角,即汽车在转向方向上的偏转角度。
还有汽车的转向半径,即汽车在转向方向上曲线行驶时所描述的圆的半径。
在汽车二自由度运动学模型中,我们可以通过一些基本方程来描述汽车的运动。
其中,前进方向的运动可以用速度方程来描述,转向方向的运动可以用转角方程来描述。
速度方程描述了汽车在前进方向上的运动速度。
根据速度方程,汽车的速度可以通过前进方向的位移和时间的比值来计算。
速度方程可以用来描述汽车在直线行驶时的运动。
转角方程描述了汽车在转向方向上的运动。
根据转角方程,汽车的转角可以通过转向方向的位移和时间的比值来计算。
转角方程可以用来描述汽车在转弯时的运动。
在实际应用中,我们可以通过测量汽车的速度和转角来推导出汽车的运动学模型。
通过分析汽车在不同条件下的运动,我们可以研究汽车的操控性能和驾驶行为。
汽车二自由度运动学模型的研究对于汽车工程和交通规划具有重要意义。
通过深入理解汽车的运动学特性,我们可以设计出更安全、更高效的汽车操控系统,提高汽车的行驶性能和驾驶舒适性。
同时,我们还可以通过运动学模型来预测汽车的运动轨迹,优化交通流量,提高道路的通行能力。
汽车二自由度运动学模型是研究汽车运动的重要工具。
通过对汽车的速度和转角进行分析,我们可以推导出汽车的运动方程,深入理解汽车的运动特性。
这对于汽车工程和交通规划具有重要意义,可以为我们设计更安全、更高效的汽车系统和交通系统提供参考。
线性二自由度汽车模型的运动微分方程
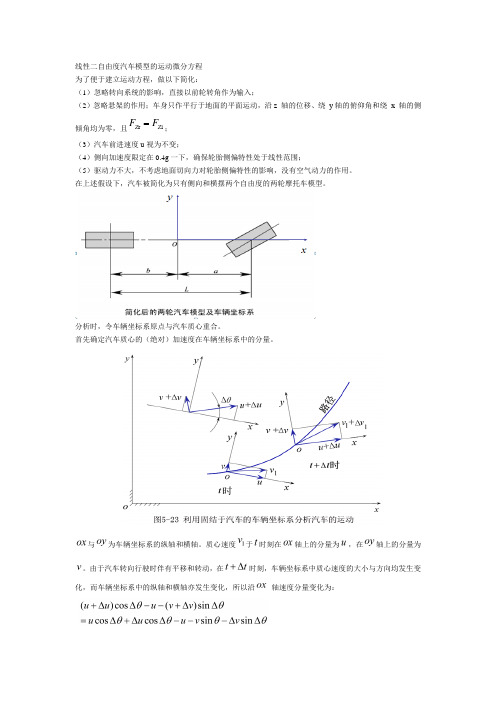
线性二自由度汽车模型的运动微分方程 为了便于建立运动方程,做以下简化:(1)忽略转向系统的影响,直接以前轮转角作为输入;(2)忽略悬架的作用;车身只作平行于地面的平面运动,沿z 轴的位移、绕 y 轴的俯仰角和绕 x 轴的侧倾角均为零,且l r Z Z F F ;(3)汽车前进速度u 视为不变;(4)侧向加速度限定在0.4g 一下,确保轮胎侧偏特性处于线性范围;(5)驱动力不大,不考虑地面切向力对轮胎侧偏特性的影响,没有空气动力的作用。
在上述假设下,汽车被简化为只有侧向和横摆两个自由度的两轮摩托车模型。
分析时,令车辆坐标系原点与汽车质心重合。
首先确定汽车质心的(绝对)加速度在车辆坐标系中的分量。
与为车辆坐标系的纵轴和横轴。
质心速度于时刻在轴上的分量为,在轴上的分量为。
由于汽车转向行驶时伴有平移和转动,在时刻,车辆坐标系中质心速度的大小与方向均发生变化,而车辆坐标系中的纵轴和横轴亦发生变化,所以沿轴速度分量变化为:考虑到很小并忽略二阶微量,上式变成:除以并取极限,便是汽车质心绝对加速度在车辆坐标系上的分量同理得:下面计算二自由度汽车的动力学方程二自由度汽车受到的外力沿轴方向的合力与绕质心的力矩和为式中,,为地面对前后轮的侧向反作用力,即侧偏力;为前轮转角。
考虑到很小,上式可以写成:下面计算二自由度汽车的动力学方程二自由度汽车受到的外力沿轴方向的合力与绕质心的力矩和为式中,,为地面对前后轮的侧向反作用力,即侧偏力;为前轮转角。
考虑到很小,上式可以写成:汽车前后轮侧偏角与其运动参数有关。
如上图所示,汽车前后轴中点的速度为,;前后轮侧偏角为,;质心侧偏角为,;为与轴的夹角,其值为:根据坐标系的关系,前后轮侧偏角为由此,可以列出外力,外力矩与汽车参数的关系式为所以,二自由度汽车的运动微分方程为由此,可以列出外力,外力矩与汽车参数的关系式为所以,二自由度汽车的运动微分方程为上式可以变形为:写成状态方程为:中。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
线性二自由度汽车模型的运动微分方程 为了便于建立运动方程,做以下简化:
(1)忽略转向系统的影响,直接以前轮转角作为输入;
(2)忽略悬架的作用;车身只作平行于地面的平面运动,沿z 轴的位移、绕 y 轴的俯仰角和绕 x 轴的侧倾角均为零,且
l r Z Z F F ;
(3)汽车前进速度u 视为不变;
(4)侧向加速度限定在0.4g 一下,确保轮胎侧偏特性处于线性范围;
(5)驱动力不大,不考虑地面切向力对轮胎侧偏特性的影响,没有空气动力的作用。
在上述假设下,汽车被简化为只有侧向和横摆两个自由度的两轮摩托车模型。
分析时,令车辆坐标系原点与汽车质心重合。
首先确定汽车质心的(绝对)加速度在车辆坐标系中的分量。
与
为车辆坐标系的纵轴和横轴。
质心速度
于时刻在
轴上的分量为
,在
轴上的分量为。
由于汽车转向行驶时伴有平移和转动,在时刻,车辆坐标系中质心速度的大小与方向均发生变
化,而车辆坐标系中的纵轴和横轴亦发生变化,所以沿
轴速度分量变化为:
考虑到很小并忽略二阶微量,上式变成:
除以并取极限,便是汽车质心绝对加速度在车辆坐标系上的分量
同理得:
下面计算二自由度汽车的动力学方程
二自由度汽车受到的外力沿轴方向的合力与绕质心的力矩和为
式中,,为地面对前后轮的侧向反作用力,即侧偏力;为前轮转角。
考虑到很小,上式可以写成:
下面计算二自由度汽车的动力学方程
二自由度汽车受到的外力沿轴方向的合力与绕质心的力矩和为
式中,,为地面对前后轮的侧向反作用力,即侧偏力;为前轮转角。
考虑到很小,上式可以写成:
汽车前后轮侧偏角与其运动参数有关。
如上图所示,汽车前后轴中点的速度为,;前后轮侧偏角为,;质心侧偏角为,;为与轴的夹角,其值为:
根据坐标系的关系,前后轮侧偏角为
由此,可以列出外力,外力矩与汽车参数的关系式为
所以,二自由度汽车的运动微分方程为
由此,可以列出外力,外力矩与汽车参数的关系式为
所以,二自由度汽车的运动微分方程为
上式可以变形为:
写成状态方程为:
中。
