磁晶各向异性机理.ppt
合集下载
磁晶各向异性PPT课件
示为： H
d
x
N
xM
x
H
d
y
N
yM
y
H
d
z
N
zM
z
NxNy Nz 1
在CGS单位值中
NaNbNc4
如果磁性体不是椭球形状，即使在均匀外场中，磁化
也是不均匀的，这时退磁场的大小和方向随位置而变，很
2难021/用3/7 退磁因子来表C示HEN。LI
23
旋转椭球的极限情况：
abc
Na
Nb
Nc
1 3
易轴
2021/3/7
CHENLI
20
三.形状各向异性
一、退磁场
当铁磁体由于磁化，在表面具有面磁极( 荷 )或体磁极( 荷 )时，在铁磁
体内将产生与磁化强度方向相反的退磁场 Hd 。若磁性体磁化是均匀的，则
退磁场也是均匀的，且与磁化强度成比例而方向相反，因此：
H d N M
N 称作退磁因子，它的大小与M无关，只依赖于样品的几 何形状及所选取的坐标，一般情况下它是一个二阶张量。
• 自发磁化:在未加外磁场时,铁磁金 属内部的自旋磁矩已经自发地排向 了同一方向的现象.
2021/3/7
CHENLI
2
磁畴
磁畴
铁磁性材料所以能使磁化强度显著增大， 在于其中存在着磁畴（Domain）结构
在未受到磁场作用时，磁畴方向是无规的， 因而在整体上净磁化强度为零
每个磁矩方向一致的区域就称为一个磁畴。 不同的磁畴方向不同，两磁畴间的区域就
A<0时，反平行排列。
2021/3/7
CHENLI
6
铁磁性的起源----直接交换相互作用
原子间距离太远，表现孤立原子特性
磁晶各项异性
试验测定：
对于立方晶体，上式仍不随方向变化，需要考虑准四极
矩相互作用能，其中与方向有关旳部分为：
Dij rij (Si rij )2 (S j rij )2
Dij rij
Cij 2 A g 2 4 A
Fe：计算值：K1 Dij 1017 erg / 原子
实测值：K1 0.541017 erg / 原子(在数量级上符合）
（二）、单离子模型
这是因为磁性离子本身旳自旋－轨道耦合作用与晶 体场旳联合效应所产生旳磁晶各向异性。
在离子化合物（如铁氧体）中，磁性离子被非磁性 离子隔开，所以磁性离子间旳各向异性互换作用较弱， 不足以产生强旳磁晶各向异性。但磁性离子受到很强旳 晶场作用，使磁电子旳状态发生变化，造成轨道动量矩 “部分冻结”，未被冻结旳那一部分轨道动量矩受晶场 旳作用被固定于某些特定旳方向上，经过自旋－轨道耦 合，使自旋磁矩在空间旳方向受到约束，从而造成各向 异性。
旳
F故k ～只能把磁偶极，矩而相其互磁作偶用极视矩为间产生相磁互晶作各用向能异仅性有
旳异性互换作用产生于电子旳自旋－轨道
耦合与各向同性旳海森堡互换作用旳联合效应。
在电子自旋旳相互作用中，除了各向同性旳互换作
用外，还要受电子自旋矩与轨道矩之间旳耦合作用旳影
响。分布于晶格上旳原子或离子，因为受到领近原子旳
c. 易锥面时
HK
(2Ku1 / Ku2 )(Ku1 2Ku2 ) 0M s
单轴各向异性
Ku1,Ku2
易磁化方向 0：与C轴夹角
Ku1>0
Ku2<0
Ku1+Ku2>0 Ku1+Ku2<0 Ku1+2Ku2<0 Ku1+2Ku2>0
第讲磁晶各向异性和磁轴伸缩PPT课件
第八章 磁性物理
本章提要
在其他章节中，对物质的导电性能等进行了介 绍。本章将介绍物质的磁性。着重介绍物质的 磁性来源，原子磁矩的计算，各种材料中原子 磁矩的计算原则。进一步介绍物质磁性的分类，
性的分子场理论，物质铁磁性的来源，亚铁磁 性的超交换理论。也介绍了铁磁性物质内部的 能量和磁畴的形成。
8.6 铁磁体中的磁晶各向异性、磁致伸缩
大块铁磁体磁化到饱和后，退磁能要大大地提 高，它迫使铁磁体分成畴。磁畴的大小、形状、 取向与铁磁体的磁晶各向异性能、退磁场能、 磁弹性能、交换能等有关。
交换能是近程的，属于静电性质的，其数 值比其它各项能量大3~4个数量级。其它各 项能量属于静磁相互作用性质的。
1．磁晶各向异性能
在单晶体的不同晶体学方向上，其光学、电 学、热膨胀、力学和磁学性能都不同。这种 特性称为晶体的各向异性 单晶体的磁性各向异性称为磁晶各向异性 (magnetic anisotropy) 磁晶各向异性能Ek定义为饱和磁化强度矢量在 铁磁体中取不同方向而改变的能量。很明显， 磁晶各向异性能是磁化强度方向的函数。
当晶体的磁致伸缩是各向同性或者是多晶时， 则λ100=λ111==λ0
λs=λ0*3/2(α1β1+α2β2+α3β3-1/3) = λ0*3/2（cos2θ- 1/3）
式中θ是磁化强度矢量方向与测量方向之 间的夹角。当θ=0,λs=λ0; θ=π/2, λs=-λ0/2， 说明当纵向伸长时，横向要收缩。
稀土元素的轨道磁矩没有淬灭，所以轨道 和自旋间存在耦合作用很强，它的磁晶各向 异性要大于3d过渡族元素。利用它的大磁晶 各向异性，可以制备永磁材料。
2 退磁场能
实验表明，磁性材料被磁化后，只要材料不 是闭合形状或者无限长，材料内部的总磁场 H将小于外磁场He 这是因为非闭合的磁性材料被磁化后在其端 面将会有正负磁荷出现。这些磁荷将在材料 内外产生一个退磁场Hd，Hd的方向在材料内 部与He和M方向向反，其作用是削弱外磁场。 退磁场越大，材料磁化越不容易
本章提要
在其他章节中，对物质的导电性能等进行了介 绍。本章将介绍物质的磁性。着重介绍物质的 磁性来源，原子磁矩的计算，各种材料中原子 磁矩的计算原则。进一步介绍物质磁性的分类，
性的分子场理论，物质铁磁性的来源，亚铁磁 性的超交换理论。也介绍了铁磁性物质内部的 能量和磁畴的形成。
8.6 铁磁体中的磁晶各向异性、磁致伸缩
大块铁磁体磁化到饱和后，退磁能要大大地提 高，它迫使铁磁体分成畴。磁畴的大小、形状、 取向与铁磁体的磁晶各向异性能、退磁场能、 磁弹性能、交换能等有关。
交换能是近程的，属于静电性质的，其数 值比其它各项能量大3~4个数量级。其它各 项能量属于静磁相互作用性质的。
1．磁晶各向异性能
在单晶体的不同晶体学方向上，其光学、电 学、热膨胀、力学和磁学性能都不同。这种 特性称为晶体的各向异性 单晶体的磁性各向异性称为磁晶各向异性 (magnetic anisotropy) 磁晶各向异性能Ek定义为饱和磁化强度矢量在 铁磁体中取不同方向而改变的能量。很明显， 磁晶各向异性能是磁化强度方向的函数。
当晶体的磁致伸缩是各向同性或者是多晶时， 则λ100=λ111==λ0
λs=λ0*3/2(α1β1+α2β2+α3β3-1/3) = λ0*3/2（cos2θ- 1/3）
式中θ是磁化强度矢量方向与测量方向之 间的夹角。当θ=0,λs=λ0; θ=π/2, λs=-λ0/2， 说明当纵向伸长时，横向要收缩。
稀土元素的轨道磁矩没有淬灭，所以轨道 和自旋间存在耦合作用很强，它的磁晶各向 异性要大于3d过渡族元素。利用它的大磁晶 各向异性，可以制备永磁材料。
2 退磁场能
实验表明，磁性材料被磁化后，只要材料不 是闭合形状或者无限长，材料内部的总磁场 H将小于外磁场He 这是因为非闭合的磁性材料被磁化后在其端 面将会有正负磁荷出现。这些磁荷将在材料 内外产生一个退磁场Hd，Hd的方向在材料内 部与He和M方向向反，其作用是削弱外磁场。 退磁场越大，材料磁化越不容易
磁晶各向异性
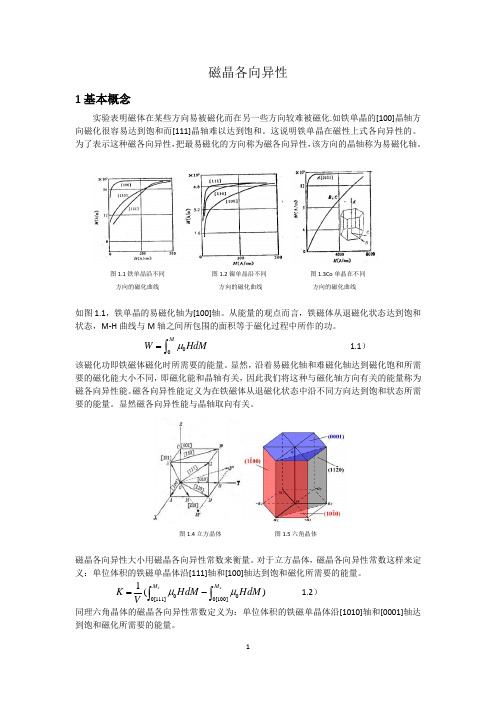
磁晶各向异性1基本概念实验表明磁体在某些方向易被磁化而在另一些方向较难被磁化.如铁单晶的[100]晶轴方向磁化很容易达到饱和而[111]晶轴难以达到饱和。
这说明铁单晶在磁性上式各向异性的。
为了表示这种磁各向异性，把最易磁化的方向称为磁各向异性，该方向的晶轴称为易磁化轴。
图1.1铁单晶沿不同 图1.2镍单晶沿不同 图1.3Co 单晶在不同 方向的磁化曲线 方向的磁化曲线 方向的磁化曲线如图1.1，铁单晶的易磁化轴为[100]轴。
从能量的观点而言，铁磁体从退磁化状态达到饱和状态，M -H 曲线与M 轴之间所包围的面积等于磁化过程中所作的功。
00MW HdM μ=⎰ 1.1）该磁化功即铁磁体磁化时所需要的能量。
显然，沿着易磁化轴和难磁化轴达到磁化饱和所需要的磁化能大小不同，即磁化能和晶轴有关，因此我们将这种与磁化轴方向有关的能量称为磁各向异性能。
磁各向异性能定义为在铁磁体从退磁化状态中沿不同方向达到饱和状态所需要的能量。
显然磁各向异性能与晶轴取向有关。
图1.4立方晶体 图1.5六角晶体磁晶各向异性大小用磁晶各向异性常数来衡量。
对于立方晶体，磁晶各向异性常数这样来定义：单位体积的铁磁单晶体沿[111]轴和[100]轴达到饱和磁化所需要的能量。
000[111]0[100]1()ss M M K HdM HdM V μμ=-⎰⎰ 1.2）同理六角晶体的磁晶各向异性常数定义为：单位体积的铁磁单晶体沿[1010]轴和[0001]轴达到饱和磁化所需要的能量。
000[1010]0[0001]1()ss M M K HdM HdM V μμ=-⎰⎰ 1.3）结合图1.1、图1.2、图1.3可知铁单晶、钴单晶的K 为正值而镍单晶的K 为负值。
2单轴磁晶各向异性磁晶各向异性可以为单轴磁晶各向异性和多轴磁晶各向异性。
单轴各向异性是磁晶各向异性的最简单形式，即自发磁化的稳定方向即易磁化方向平行于某一特殊晶轴。
如六方晶系钴的自发磁化方向平行于 C 轴，这就表现出强的单轴各向异性。
磁晶与向异性与磁轴伸缩课件
磁晶与向异性的应用领域
磁晶的应用领域
磁晶在电子、通讯、能源等领域有广泛应用，如用于制造磁记录材料、磁传感 器、磁存储器等。
向异性的应用领域
向异性在电子、通讯、能源等领域也有广泛应用，如用于制造高灵敏度磁力计 、电磁波吸取材料、电磁波屏蔽材料等。
02
磁晶的分类与特性
铁磁性磁晶
铁磁性磁晶是指具有强磁性的磁晶，其磁矩 方向可以自发地排列成一致的方向，产生强 烈的磁场。常见的铁磁性磁晶有铁、钴和镍 等。
要点二
磁性材料在医疗科技领域的发展 前景
随着医疗技术的不断进步和人们对健康需求的不断增加， 磁性材料在医疗科技领域的应用前景非常广阔。未来，磁 性材料将更加重视个性化、精准化和智能化，同时不断探 索新的应用领域，如基因治疗和细胞治疗等领域。
感谢您的观看
THANKS
铁氧体磁晶具有较高的磁导率和较低的损耗等特性，因此在通讯、雷达和导航等领 域有广泛的应用。
铁氧体磁晶还可以通过掺杂其他元素来调节其性能，如调节电阻率、介电常数和热 稳定性等，这使得它们在电子器件和传感器等领域具有一定的应用前景。
03
向异性的分类与特性
单轴向异性
单轴向异性是指只有一个易磁化方向的材料特性。
向异性是指磁性材料在不同方向 上表现出不同的物理性质，如磁 化强度、磁导率等。
磁晶与向异性的物理特性
磁晶的物理特性
磁晶具有自发磁化和磁畴结构等特性 ，这些特性决定了磁晶的磁学性质和 磁学行为。
向异性的物理特性
向异性表现为磁性材料在不同方向上 具有不同的物理性质，如磁导率、磁 化强度等。这种特性使得磁性材料在 某些方向上具有更高的磁学性能。
反铁磁性磁晶还具有较高的电阻率和 较低的介电常数等特性，这使得它们 在电子器件和集成电路等领域具有一 定的应用前景。
课件7磁晶各项异性1
二、磁各向异性类型 按其起源物理机制可分为： 磁晶各向异性 磁性单晶体所固有的 • 磁形状各向异性：
●
反映沿磁体不同方向磁化与磁体几何形状有关的特性。
磁矩取向一致→退磁场→退磁场能（取决于磁体的几 何形状，如：由细长微粒组成的磁体、磁性薄膜）→ 显出很强的形状各向异性 • 磁应力各向异性：
CoO薄膜 • 交换磁各向异性： 将强磁性的Co微粒表面进行微弱 氧化，形成薄层CoO，由于Co是铁磁 Co 性的，而CoO是反铁磁性的，在Co与 包Co粒子 CoO界面就有交换作用，当磁场热处理 后，由此引起交换各向异性（做成磁带，录音效果好）。
单轴各向异性
Ku1,Ku2
易磁化方向 0：与C轴夹角 EA 各向异性磁场 HA HA Ku1>0 Ku1+Ku2>0 Ku1<0 Ku1+2Ku2>0 sin0=(-Ku1/2Ku2)1/2 园锥面， -Ku12/4Ku2 2( Ku1/Ku2 )x ( Ku1+2Ku2 )/IS 36│K3│sin40/IS
∴可将B3、B5项并入B0及B6项 最后，立方晶体的磁晶各向异性能 Fk i 的数学表 达式为：
Fk K 0 K1 (1 2 ＋ 2 3 ＋ 3 1 )
2 2 2 2 2 2
K 21 2 3 ......
2 2 2
一般在考虑Fk相对于Ms取向变化时，常将K0略去：
反映磁体内磁化强度矢量取向与应力方向有关的特性。
• 感生磁各向异性：
许多铁磁性合金与铁氧体中，通过对磁体施以某种
方向性处理的工艺，可以感生出磁各向异性。 感生各向异性又可分为： • 磁场热处理感生各向异性 • 弹性形变感生各向异性
• 生长感生各向异性
实验课件PPT各向异性磁阻效应
线圈半径 80mm
线圈匝数 520
20.0mm
70.0mm
磁阻效应综合实验·实验内容
3. 实验内容 （2）实验步骤及注意事项
c. 传感器标尺杆读数
亥姆霍兹线圈中 心位置
元件在亥姆霍兹线 圈中心位置时读数 120.0mm
以亥姆霍兹线圈中心为原点，元件的轴上坐标x与左侧读数x'的关系
x x 120
磁阻效应综合实验·实验内容
a. 如果大小恒定、方向可变的外加弱磁场（不导致灵敏度下降）与图13-1 中“磁敏感方向”相同或相反时，传感器电桥上每一个臂的坡莫合金薄 膜电阻如何变化？电桥输出电压如何变化？
b. 为什么测量各向异性磁阻传感器的输出电压时，要改变 B测为相反方向 （或改变励磁电流方向）各测量一次？
c. 为什么亥姆霍兹线圈轴线中点附近磁场是均匀的？本实验两线圈之间距 离多少毫米、两线圈间及与电源如何连接时可以组成亥姆霍兹线圈？请 画出接线图。
arctg(Bz B// )
成都地磁参数公认值： 水平磁偏角：1o11.16 ‘；
水平分量：34.48uT； 竖直分量：36.43uT。
θ 是相对于实验桌的水平 磁偏角，相对于北极的水 平磁偏角为θ 加上实验桌 的方位角θ桌 。
磁阻效应综合实验·实验内容
3. 实验内容 （1）实验测试内容
a. 用亥姆霍兹线圈磁场对磁阻传感器定标 b. 测量电源电压对传感器灵敏度的影响。 c. 测量单线圈、两线圈极性不同时轴线磁感应强度分布。 d. 用磁阻效应传感器测量地磁场的大小和方位。
θ
θ
45o+δ
45o- δ I
I ΔR↘
M0 ΔR↗ B
接地
M0 B
+ 输出电压U0 －
磁晶各项异性 PPT
磁晶各项异性
4-3 磁晶各向异性常数得测量方法 一、单晶体磁化曲线法
W Ms HdM 0
1、沿[100]方向(x轴)磁化
W[100] K0
2、沿[110]轴磁化:
W[110]
K0
K1 4
3、沿[111]轴磁化:
W[111]
K0
K1 3
K2 27
W
W[110] W[100] [111] W [100] K1
用,使电子轨道矩失去了在空间得方向对称性,通过电子自
旋矩与轨道矩得耦合作用,便产生了电子自旋间各向异性
得交换作用能。范弗列克称之为“准
偶极矩相互作用”或“各向异性交换作用”
这个能量表达式与磁偶极矩作用能类似,可写为:
U各向异性
Cij i j
rij
Si S j
3(Si
rij )(S rij 2
K1
4 K2
3 27
二、磁转矩法
转矩磁强计得原理就是,当样品(片状或 球状)置于强磁场中,使样品磁化到饱与。若 易磁化方向接近磁化强度得方向,则磁晶各 向异性将使样品旋转,以使易轴与磁化强度 方向平行这样就产生一个作用在样品上得 转矩。如果测量转矩与磁场绕垂直轴转过 得角度关系,就可以得到转矩曲线,并由此可 求得磁晶各向异性常数。
0=/2
C面, ⊥
sin0=(Ku园1/2锥Ku面2)1，/2
EA 各向异性磁场
HA HA
0
2Ku1/Ms 0 ( C轴 )
Ku1+Ku2
-Ku12/4Ku2
2( Ku1/Ku2 )x -2(Ku1+2Ku2)/MS ( Ku1+2Ku2 )/MS
36│K3│/ MS ( C面 ) 36│K3│sin40/MS
4-3 磁晶各向异性常数得测量方法 一、单晶体磁化曲线法
W Ms HdM 0
1、沿[100]方向(x轴)磁化
W[100] K0
2、沿[110]轴磁化:
W[110]
K0
K1 4
3、沿[111]轴磁化:
W[111]
K0
K1 3
K2 27
W
W[110] W[100] [111] W [100] K1
用,使电子轨道矩失去了在空间得方向对称性,通过电子自
旋矩与轨道矩得耦合作用,便产生了电子自旋间各向异性
得交换作用能。范弗列克称之为“准
偶极矩相互作用”或“各向异性交换作用”
这个能量表达式与磁偶极矩作用能类似,可写为:
U各向异性
Cij i j
rij
Si S j
3(Si
rij )(S rij 2
K1
4 K2
3 27
二、磁转矩法
转矩磁强计得原理就是,当样品(片状或 球状)置于强磁场中,使样品磁化到饱与。若 易磁化方向接近磁化强度得方向,则磁晶各 向异性将使样品旋转,以使易轴与磁化强度 方向平行这样就产生一个作用在样品上得 转矩。如果测量转矩与磁场绕垂直轴转过 得角度关系,就可以得到转矩曲线,并由此可 求得磁晶各向异性常数。
0=/2
C面, ⊥
sin0=(Ku园1/2锥Ku面2)1，/2
EA 各向异性磁场
HA HA
0
2Ku1/Ms 0 ( C轴 )
Ku1+Ku2
-Ku12/4Ku2
2( Ku1/Ku2 )x -2(Ku1+2Ku2)/MS ( Ku1+2Ku2 )/MS
36│K3│/ MS ( C面 ) 36│K3│sin40/MS
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
种相互作用被称为赝偶极相互作用
机理：部分未淬灭的轨道矩与自旋相互耦合，随着磁化强度的 转动，通过轨道波函数重叠的变化，导致交换能发生变化。
第三项为起源相同的高价项，称为四极相互作用。磁晶各向 异性可以通过对晶体中所有自旋对的能量相加而计算出来
这模型称为自旋对(spin-pair)模型。
EA wi
w L S LS cos
二重态
在立方晶体中有四个<111>轴， 若离子平均的分布在具有不同的 <111>轴的八面体间隙位。
EA
1 NLS
4
cos1
cos2
cos3
cos4
式中1 ,2 ,3 ,4为自旋磁矩与四个<111>轴的夹角
EA
1 NLS
4
cos1
cos2
cos3
cos4
付里叶级数展开
EA
Hale Waihona Puke 32135NLS
(12
2 2
22
2 3
2 2
31
)
由于Co2+具3d7，过半滿时自旋-轨道耦合常数为负，<0，式中 各向异性常数为正值，K1>0。
在许多K1<0的铁氧体中，掺入钴后K1变为正值。
3、 4f 稀土离子和合金的磁晶各向异性
三、磁晶各向异性机理
1、自旋对模型
磁晶各向异性：晶体的内能随磁化强度 方向的变化而变化。当自发磁化强度从 一个方向转向另一个方向。相邻自旋保 持平行，这是因为自旋间存在强的交换 作用，自旋Si和Sj间的交换作用为
Wij 2JSi S j 2JS 2 cos
其中，为S自旋的大小，而是Si 和Sj 间的夹角。右图自旋从a旋转到b所有 自旋保持平行，因而=0,交换能不改 变。
22
3) 35
....
l
(32
1) 3
q(34
6 7
32
3) 35
....
Nq 14 24 34 常数
2Nq 1222 2232 3212 常数
EA 2Nq 1222 2232 3212
N为单位体积内的总原子数，
K1 2Nq
对体心立方晶格，计算得到
K1
16 9
Nq
对面心立方晶体，得到
负电的电子轨道与O2-之间的 库仑排斥势使体系自由能增加。
钴离子电子中未半满的二个电子分 别占据的一重态和简并的二重态。 占据二重简并能级的电子，可在两 个可能的波函数间交替变化，形成 一个环形轨道，产生一个轨道磁矩 与钴离子总自旋磁矩相互作用，形 成磁晶各向异性。
B. 单离子模型定量计算：
简单计算磁各向异性能，设二重态 产生轨道磁矩为± L,自旋-轨道耦 合能w为
以钴铁氧体Co2+Fe23+O4为例。一个Fe3+ 占据四面体位置。 Co2+( 3d7 )和 Fe3+( 3d5 )占据八面体位置。
在晶场作用下，钴离子轨道角动量劈裂为d 二重态和d三重态
z
O2-
y
x Co2+
d
d
立方晶场
相互作用能高
相互作用能低
钴离子次近邻的三个金属离子相对于三角对称轴对称地分布，它 们产生的三角晶场，使三重态d劈裂为一个单重态和一个二重态。 dxy和dzx ,dyz 。
F kT Ni ln Zi
i
Zi
eE j (i ) / kT
j
i 代表不同的次晶格，Ni 单位体积中i 次晶格上的磁性
离子数，i 是次晶格上磁性离子的平均自旋方向与晶场 对称轴的夹角。Ej(i)为i次晶格上磁性离子的微观各向
异性能， 是对i 次晶格上的磁性离子的量子态求和。
j
A. 单离子模型定性描述：
d 波函数沿着两个立方轴之间的方向展开，避开了O2-库仑排斥
能相对较小。三角晶场是正的，沿[111]轴展开的单重态能量较低， 垂直[111]展开的二重态能量较高。( Jahn-Trller effect ),
二重态
dzx,dyz dxy
d d
d
自由离子
立方
三角
二重态
d
三角晶场
d 波函数沿立方轴展开，带
l
3M 2
4 0r
3
则它与磁偶极相互作用有相同的形式。
w(cos) g l(cos2 1) q(cos4 6 cos2 3 ) ......
3
7
35
然而真正测得的磁各向异性相应的l 值比此项给出的值大
100到1000倍。因此产生磁晶各向异性的机制不是偶极相互
作用，虽然形式相同，但其系数是来源于磁晶各向异性，这
K1 Nq
由于
2 i
1
即偶极项，对立方晶系各向异性没有贡献。
但是对单i轴各向异性有贡献。一般l比q大1-2个数量级。如
Co的Ku为105Jm-3；Fe的K1为103-104Jm-3
自旋对模型对金属和合金是适用的。对氧化物和化合物不适用。
2、单离子模型
自旋-轨道相互作用：在结晶体中原子间是通过静电库仑相互作 用相结合，对原子中的电子自旋磁矩没有作用，但是对电子轨道 有强烈的静电相互作用，而使电子轨道劈裂。电子轨道磁矩与自 旋磁矩的相互作用形成自旋-轨道的耦合，其作用能为
cos cos2 cos4 ..... 18 cos2 8 cos4 ....
3
15
15
15
代入EA中，得到
Ea
1 4
N LS
18
45
1 2 3 2 1 2 3 2 1 2 3 2 1 2 3 2
18 135
1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4
交换能是各向同性。
要解释磁晶各向异性，必须考虑含有晶轴的能量项。
如果假设自旋与原子连线的夹角 为，则自旋对的能量经勒让德 多项式展开为
w(cos) g l(cos2 1) q(cos4 6 cos2 3 ) ......
3
7
35
第一项与无关，对应于交换相互作用
第二项称为偶极相互作用，因为若系数是
rr
ELS L S
A原子
晶场
B原子
自 旋
自旋 轨道 相互 作用
轨 道
原子间静 电 库仑相 互作用
轨 道
自旋 轨道 相互 作用
自 旋
单离子模型是假定晶体中的磁性离子都是彼此独立的，
晶体的宏观磁晶各向异性就是这些磁性离子的微观磁晶
各向异性的统计平均值。根据玻耳兹曼的统计理论，宏
观自由能密度F与磁性离子微观能量E( i)的关系为
i
i表示自旋对。仅考虑近邻，最多到次近邻之间的相互作用。
设(1,2,3 )为平行自旋对的方向余弦。
对原子连线方向与x-轴平行的自旋对，cos可以用1代替，
对平行y-,z-轴的自旋对，cos可分别用2和3替代。
l(12
1) 3
q(14
6 7
12
3) 35
....
EA
N
l
(
2 2
1) 3
q(24
6 7