反比例函数比例系数k的几何意义
26.1.2反比例函数中比例系数k的几何意义

2 5、S⊿ABC的面积=____
6、(2009年重庆市)如图所示.如果函数y=-kx(k≠0)
4 与 y x 图像交于A、B两点,过点A作AC垂直
于y轴,垂足为点C,则△BOC的面积为
2
.
S⊿AOC =∣-4 ∣= 2 S ⊿BOC =S ⊿AOC
D
2 7、四边形ABCD的面积=_____
o
A
x
想一想
y P(m,n) o A x
若将此题改为过P点 作y轴的垂线段,其结 论成立吗?
y A o P(m,n) x
S OAP
1 1 1 OA AP | m | | n | | k | 2 2 2
(3)设P(m, n)关于原点的对称点是 P (m,n), 过P作x轴的垂线 与过P作y轴的垂线交于A点, 则
y
A
O S
2
S1
B
x
A. S1>S2 B.S1<S2 C.S1=S2 D.S1与S2的大小关系 不能确定
C
D
的图象 如图所示,点M是该函数图象上一点,MN垂直 于x轴,垂足是点N,如果S△MON=2, 则k的值 为( C ) (A)2 (B)-2 (C) -4 (D) 4
y
2、 (2010山东省中考题) 反比例函数y=
y
y
B
P(m,n)
A
B
P(m,n) A
o
x
o
x
k 设P(m, n)是双曲线y (k 0)上任意一点, 有 : x (2)过P作x轴的垂线, 垂足为A, 则
SOAP 1 1 1 OA AP | m | | n | | k | 2 2 2
反比例函数中比例系数k的几何意义

反思小结
在反比例函数 y 10 的图象上,有一系列点A1,A2, x A3…..An,An+1,若A1横坐标为2,且以后每点的 横坐标与它前一个点的横坐标的差都为2. 现分别 过点A1,A2,A3…..An,An+1作X轴与Y轴的垂线 段,构成若干个矩形如图10所示,将图中阴影部 分的面积从左到右依次记为S1、S2、S3、…Sn, 5 5 15 2 5 2 (5 _____, ) 则S1=________, S +S +S =____ S1+S2 2 1 2 3 4 2 5 10 n 2 (5 ) +S3+….+Sn=________________.( 用n的代数式表 n 1 n 1 A 示)
C
S SOAD SABD SBCD SOCD 4 1 4
达标测试
已知几何图形的面积S,求比例系数k
5、如图,已知双曲线 (k>0) 经过矩形OABC边AB的中点F,交BC于点E, 且四边形OEBF的面积为2,则k的值为( B )。
y
y
k x
A 1
所以
B 2
C 4
S OAB 4
O
y
已知几何图形的面积S,求比例系数k k y 变式、如图,已知双曲线 x ( k>0 )经
B
D
C E A
x
而
SOAB SOBC SOAC
即
S ODE 1 S OAB 1 4 k 3 2
1 k 2
相似三角形的面积比 等于相似比的平方 k 4;
k 0 k 4
k 0 k 4
4 y x
达标测试
4、如图,在平面直角坐标系中, 点O为原点,菱形OABC的对角线 OB在x轴上,顶点A在反比例函数 2 的图像上,求菱形的面积。 y B
反比例函数中k的几何意义的应用

反比例函数中k的几何意义的应用
k在反比例函数中具有重要的几何意义,以下列举一些它的应用。
1. 直线反比例函数:k反映直线斜率的倒数,即斜率m=-k。
当给定直
线k值时,由定点和k值可以求出斜率m,从而可以绘制出这条直线。
2. 圆反比例函数:k反映圆半径r的倒数,即r=1/k。
当给定圆k值时,由定点和k值可以求出圆半径,从而可以绘制出这个圆。
3. 抛物线反比例函数:k反映抛物线的开口方向,当k > 0时,抛物线
向右开口;当k < 0时,抛物线向左开口。
4. 双曲线反比例函数:k反映双曲线的开口方向,当k>0时,双曲线
开口向右;当k<0时,双曲线开口向左。
5. 其他函数反比例函数:k可以反映此类函数中曲线的凹凸,当k > 0时,曲线是凹曲线;当k < 0时,曲线是凸曲线。
总之,k在反比例函数中应用广泛,几乎所有的函数都可以用反比例函
数表示。
它的几何意义非常重要,不仅仅可以根据k值绘制出各种曲线,而且可以了解曲线的开口方向以及凹凸方向。
因此,k在反比例函
数绘制中发挥着重要的作用。
反比例函数中k的几何意义是什么

反比例函数中k的几何意义是什么
反比例函数中k的几何意义是什么
发现学生对反比例函数中K的几何意义理解的不好,造成在面对一些反比例函数与几何图形相结合的问题时的束手无策,要想解决好这个问题,这就要求我们老师在辅导学生时要敢于花大力气帮助学生深刻理解K的几何意义,下面是店铺给大家整理的反比例函数中k的几何意义简介,希望能帮到大家!
反比例函数中k的几何意义
过反比例函数y=k/x(k≠0),图像上一点P(x,y),作两坐标轴的`垂线,两垂足、原点、P点组成一个矩形,矩形的面积S=x的绝对值*y的绝对值=(x*y)的绝对值=|k|
研究函数问题要透视函数的本质特征。
反比例函数中,比例系数k 有一个很重要的几何意义,那就是:过反比例函数图象上任一点P作x 轴、y轴的垂线PM、PN,垂足为M、N则矩形PMON的面积S=PM·PN=|y|·|x|=|xy|=|k|。
所以,对双曲线上任意一点作x轴、y轴的垂线,它们与x轴、y轴所围成的矩形面积为常数。
从而有k的绝对值。
K的几何意义与三角形相似知识的关联
【反比例函数中k的几何意义是什么】。
中考数学复习考点知识归类讲解12 反比例函数比例系数k的几何意义

中考数学复习考点知识归类讲解 专题12 反比例函数比例系数k 的几何意义知识对接考点一、反比例函数比例系数k 的几何意义(1)意义:从反比例函数y =(k≠0)图象上任意一点向x 轴和y 轴作垂线,垂线与坐标轴所围成的矩形面积为|k|,以该点、一个垂足和原点为顶点的三角形的面积为1/2|k|. (2)常见的面积类型:失分点警示已知相关面积,求反比例函数的表达式,注意若函数图象在第二、四象限,则k <0. 例:已知反比例函数图象上任一点作坐标轴的垂线所围成矩形为3,则该反比例函数解析式为:3y x=或3y x =-专项训练 一、单选题1.如图,已知反比例函数2y x=-的图像上有一点P ,过点P 作PA x ⊥轴,垂足为点A ,则POA 的面积是()A.2 B.1 C.1-D.122.如图,在平面直角坐标系中,A,B是反比例函数kyx=在第一象限的图象上的两点,且其横坐标分别为1,4,若AOB的面积为54,则k的值为()A.23B.1C.2D.1543.若图中反比例函数的表达式均为4yx=,则阴影面积为4的有()A.1个B.2个C.3个D.4个4.如图,点A是反比例函数4yx=-图象上的一个动点,过点A作AB⊥x轴,AC⊥y轴,垂足分别为B,C,则矩形ABOC的面积为()A .-4B .2C .4D .85.如图,等腰ABC 中,5AB AC ==,8BC =,点B 在y 轴上,//BC x 轴,反比例函数k y x=(0k >,0x >)的图象经过点A ,交BC 于点D .若AB BD =,则k 的值为()A .60B .48C .36D .206.在平面直角从标系中,30°的直角三角尺直角顶点与坐标原点重合,双曲线11k y x=(x >0),经过点B ,双曲线22k y x=(x <0),经过点C ,则12k k =( )A.﹣3 B.3 C.D7.如图,A、B是双曲线y=kx图象上的两点,过A点作AC⊥x轴于点C,交OB于点D,BD=2OD,且ADO的面积为8,则DCO的面积为()A.12B.1 C.32D.28.如图,平行于y轴的直线l分别与反比例函数kyx=(x>0)和1yx=-(x>0)的图象交于M、N两点,点P是y轴上一动点,若△PMN的面积为2,则k的值为()A.2 B.3 C.4 D.59.如图,过x轴正半轴上的任意一点P,作y轴的平行线,分别与反比例函数y3=x(x>0)和y6=x-(x>0)的图象交于B、A两点.若点C是y轴上任意一点,则△ABC的面积为()A .3B .6C .9D .9210.如图.在平面直角坐标系中,△AOB 的面积为278,BA 垂直x 轴于点A ,OB 与双曲线y =k x相交于点C ,且BC ∶OC =1∶2,则k 的值为()A .﹣3B .﹣94C .3D .92二、填空题11.如图,平面直角坐标系中,O 是坐标原点,点A 是反比例函数()0k y k x=≠图象上的一点,过点A 分别作AM x ⊥轴于点M ,AN y ⊥轴于点N .若四边形AMON 的面积为12,则k 的值是__________.12.如图,在反比例函数3yx=的图象上有一动点A,连接AO并延长交图象的另一支于点B,在第二象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数kyx=的图象上运动,tan∠CAB=2,则k的值为_____13.如图,点P在反比例函数4yx=-的图像上,过点P作PA x⊥轴于点A,则POA的面积是_______.14.如图所示,反比例函数kyx=(0k≠,0x>)的图像经过矩形OABC的对角线AC的中点D .若矩形OABC 的面积为8,则k 的值为________.15.如图,点A 与点B 分别在函数11(0)k y k x =>与220)k y k x=<(的图象上,线段AB 的中点M 在y 轴上.若△AOB 的面积为3,则12k k -的值是___.三、解答题16.如图,一次函数122y x =-的图象分别交x 轴、y 轴于A 、B ,P 为AB 上一点且PC 为AOB 的中位线,PC 的延长线交反比例函数ky x=(0k >)的图象于点Q ,32OQCS=.(1)求A 点和B 点的坐标; (2)求k 的值和Q 点的坐标.17.点O 为平面直角坐标系的原点,点A 、C 在反比例函数a y x=的图象上,点B 、D 在反比例函数b y x=的图象上,且0a b >>.(1)若点A 的坐标为()6,4,点B 恰好为OA 的中点,过点A 作AN x ⊥轴于点N ,交b y x=的图象于点P . ①请求出a 、b 的值; ②试求OBP 的面积.(2)若////AB CD x 轴,32CD AB ==,AB 与CD 间的距离为6,试说明-a b 的值是否为某一固定值?如果是定值,试求出这个定值;若不是定值,请说明理由.18.如图,点C 在反比例函数y 1=x的图象上,CA ∥y 轴,交反比例函数y 3=x的图象于点A ,CB ∥x 轴,交反比例函数y 3=x的图象于点B ,连结AB 、OA 和OB ,已知CA =2,则△ABO 的面积为__.19.如图是反比例函数2yx=与反比例函数在第一象限中的图象,点P是4yx=图象上一动点,PA⊥X轴于点A,交函数2yx=图象于点C,PB⊥Y轴于点B,交函数2yx=图象于点D,点D的横坐标为a.(1)用字母a表示点P的坐标;(2)求四边形ODPC的面积;(3)连接DC交X轴于点E,连接DA、PE,求证:四边形DAEP是平行四边形.20.如图,点A(﹣2,y1)、B(﹣6,y2)在反比例函数y=kx(k<0)的图象上,AC⊥x轴,BD⊥y轴,垂足分别为C、D,AC与BD相交于点E.(1)根据图象直接写出y1、y2的大小关系,并通过计算加以验证;(2)结合以上信息,从①四边形OCED的面积为2,②BE=2AE这两个条件中任选一个作为补充条件,求k 的值.你选择的条件是(只填序号). 21.如图,一次函数()20y kx k k =-≠的图象与反比例函数1(10)m y m x-=-≠的图象交于点C ,与x 轴交于点A ,过点C 作CB y ⊥轴,垂足为B ,若3ABC S =△.(1)求点A 的坐标及m 的值;(2)若AB =22.如图,过C 点的直线y =﹣12x ﹣2与x 轴,y 轴分别交于点A ,B 两点,且BC =AB ,过点C 作CH ⊥x 轴,垂足为点H ,交反比例函数y =k x(x >0)的图象于点D ,连接OD ,△ODH 的面积为6(1)求k 值和点D 的坐标;(2)如图,连接BD ,OC ,点E 在直线y =﹣12x ﹣2上,且位于第二象限内,若△BDE 的面积是△OCD 面积的2倍,求点E 的坐标.11 / 11 23.如图,直线l 分别交x 轴,y 轴于A 、B 两点,交反比例函数(0)k y k x =≠的图象于P 、Q 两点.若2AB BP =,且AOB 的面积为4(1)求k 的值;(2)当点P 的横坐标为1-时,求POQ △的面积.。
反比例函数中k的几何意义在解题中的运用
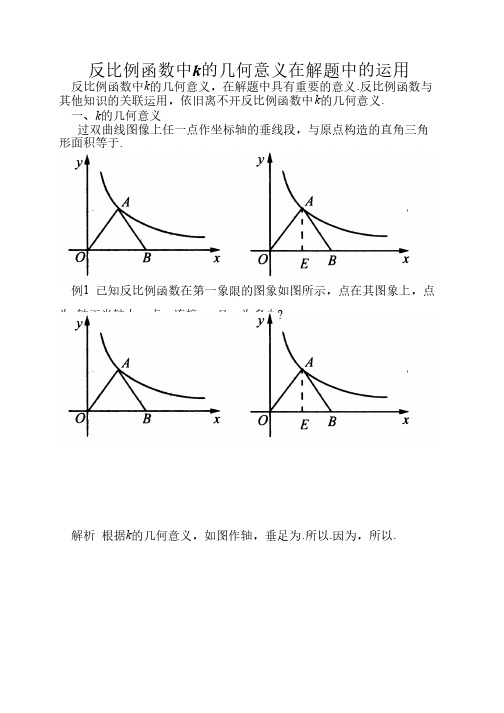
反比例函数中k的几何意义在解题中的运用反比例函数中k的几何意义,在解题中具有重要的意义.反比例函数与其他知识的关联运用,依旧离不开反比例函数中k的几何意义.一、k的几何意义过双曲线图像上任一点作坐标轴的垂线段,与原点构造的直角三角过双曲线图像上任一点作坐标轴的垂线段,与原点构造的直角三角形面积等于.已知反比例函数在第一象限的图象如图所示,点在其图象上,点例1 已知反比例函数在第一象限的图象如图所示,点在其图象上,点且,为多少?为x轴正半轴上一点,连接、,且,为多少根据k的几何意义,如图作轴,垂足为.所以.因为,所以.解析根据如图,在平面直角坐标系中,过点M(0,2)的直线l与x轴平行,且练习如图,在平面直角坐标系中,过点直线l分别与反比例函数和的图象交于点P、点Q(1)求点P的坐标;(2)若△POQ的面积为8,求k的值.因为点P在双曲线上,过M(0,2)的直线l与x轴平行,所以点P的纵解 因为点坐标为y=2,则横坐标x=3.所以点P的坐标为P(3,2)所以.因为,所以,所以或.因为图象在第二象限,所以.二、k的几何意义与线段比,面积比的知识关联如图,反比例函数的图象与矩形的两边相交于两点,若是的中例2 如图,反比例函数的图象与矩形的两边相交于两点,若是的中点,,求k的值.双曲线上存在点E与点F,根据k的几何意义,连接O E、OF,解析双曲线上存在点有.又因为点E是AB的中点,所以.可得;.所以点F是CB的中点.所以.可得.因为图象在第一象限,所以k=8.知识关联:此题用到k的几何意义、线段比与面积比的知识关联.三、k的几何意义与三角形相似知识的关联例3 如图,一次函数的图象与轴交于点如图,一次函数的图象与轴交于点A,与反比例函数的图象交于点B, BC垂直轴于点C.若△ABC的面积为1,求k的值.因为点B在反比例函数图象上,得由,得,得假设直线与y轴解析因为点交与点D,则点D(-1,0),OD=1.BC//OD得△ABC~△ADO,可得:.由OD=1得BC=2,把y=2代入得x=1.5.所以点B坐标为(1. 5,2).把x=1. 5,y=3代入中得k=8/3.知识关联:此题用到k的几何意义、三角形相似、线段比与面积比的知识关联.如图,若双曲线与边长为5的等边的边OA, AB分别相交于C, D两练习如图,若双曲线与边长为点,且OC=3BD,求k的值.解析过点作轴于点,过点作轴于点过点作轴于点,过点作轴于点.因为为等边三角形,,可得~,所以.又因为得.设,则.可得即.在中,可得..,所以图象在第一象限,所以作为九年级复习阶段,做好知识间的关联学习,对构成学生的知识系统具有很好的作用.。
反比例函数中K的几何意义
反比例函数中K的几何意义
在反比例函数中,K表示比例系数或常数,也被称为反比例常数。
它
是用来确定两个变量之间反比关系的重要参数。
反比例函数的一般形式为:y=K/x,其中K表示比例系数。
K的几何意义可以通过分析反比例函数的图像得出。
反比例函数的图
像是一个双曲线,特点是曲线趋向于两个坐标轴。
下面将详细讨论K的几
何意义。
1.K的符号对于曲线的位置以及开口方向具有重要影响。
如果K为正数,那么曲线将位于第一和第三象限,并且开口方向为右上和左下。
如果
K为负数,那么曲线将位于第二和第四象限,并且开口方向为左上和右下。
2.K的绝对值越大,曲线就越“陡峭”。
当K增大时,曲线将更加接
近于坐标轴,并且在原点附近的斜率会越来越大。
反之,当K变小时,曲
线将更加平缓,斜率将减小。
3.K决定了特定坐标点的函数值。
例如,在函数y=K/x中,当x为K 时,y的值将为1、这是因为x与y成反比关系,而K是这种关系的常数。
4.K还决定了曲线相对于坐标轴的位置。
具体而言,当K增大时,曲
线将向坐标轴移动,而当K减小时,曲线将远离坐标轴。
总之,K代表了反比例函数中的比例系数或常数,它对于函数的位置、开口方向、陡峭程度以及特定坐标点的函数值都具有重要影响。
通过对K
的分析,我们可以更好地理解和解释反比例函数的几何特征。
反比例函数中k的几何意义
【主干必备】 反比例函数中比例系数k的几何意义 设点P(m,n)是双曲线y= k (k≠0)上任意一点
x
(1)过点P作x轴或y轴的垂线,垂足为点A,则
S△OAP=
1 2
·OA·AP=
1 |m|·|n|=
2
1 |mn|=
2
1 2
|k|.
(2)过点P分别作x轴、y轴的垂线,垂足为A,B,
值为 世纪金榜导学号( D )
A.5
B.-5
C.10
D.-10
3.(2019·哈尔滨木兰期末)已知P是反比例函数y= k
x
(k≠0)图象上一点,PA⊥x轴于A,若S△AOP=4,则这个反
比例函数的解析式是 ( C )
A.y= 8
x
C.y= 8 =- 8
x
D.y= 4 或y=- 4
则S矩形OAPB=OA·AP=|m|·|n|=|mn|=|k|.
【微点警示】 因为反比例函数y= k (k是常数,k≠0)中的k有正、负之
x
分,所以在利用解析式求矩形或三角形的面积时,都应 加上绝对值符号;已知矩形或三角形的面积求反比例函 数的解析式或k的值时,要根据函数的图象所在的象限 确定k的正负.
x
x轴于点B交反比例函数y= 2 的图象于点C,连接OA,OC,
x
则△OAC的面积为 ( B )
A.2
B.3
C.6
D.8
2.(2019·达州达川区期末)如图所示,点A是反比例函
数y= k 的图象上的一点,过点A作AB⊥x轴,垂足为B,点
x
C为y轴上的一点,连接AC,BC.若△ABC的面积为5,则k的
【核心突破】
中考数学全程复习方略微专题二反比例函数中k的几何意义课件
【主干必备】 反比例函数中比例系数k的几何意义 设点P(m,n)是双曲线y= k (k≠0)上任意一点
x
(1)过点P作x轴或y轴的垂线,垂足为点A,则
S△OAP=
1 ·OA·AP=
2
1 |m|·|n|=
2
1 |mn|=
2
1 |k|.
2
(2)过点P分别作x轴、y轴的垂线,垂足为A,B, 则S矩形OAPB=OA·AP=|m|·|n|=|mn|=|k|.
2.(2019·株洲中考)如图所示,在平面直角坐标系xOy
中,点A,B,C为反比例函数y= k (k>,OC,过点A作AD⊥y轴于点D,过点B,C分别作
BE,CF垂直x轴于点E,F,OC与BE相交于点M,记△BOM,四
边形CMEF,△AOD的面积分别为S1,S2,S3,则 榜导学号( D )
世纪金
A.S1=S2+S3 C.S3>S2>S1
B.S2=S3 D.S1S2< S32
3.(2019·安顺中考)如图,直线l⊥x轴于点P,且与反比
例函数y1=
k1 x
(x>0)及y2=
k2 (x>0)的图象分别交于A,B
x
两点,连接OA,OB,已知△OAB的面积为4,则k1-k2=___8___.
x
A,B两点,过点A作AC⊥y轴于点C,过点B作BD⊥y轴于点D,
过点B作BE⊥x轴于点E,连接AD,已知AC=1,BE=1,
3
S矩形BDOE=4.则S△ACD=__2_.
类型二 求反比例函数的比例系数k
例2(2018·遵义中考)如图,直角三角形的直角顶点在
坐标原点,∠OAB=30°,若点A在反比例函数y= 6 (x>0)
反比例函数k的几何意义
知识讲解1.反比例函数的概念如图所示,过双曲线)0(k≠=kxy上任一点),(yxP作x轴、y轴的垂线PM、PN,垂足为M、N,所得矩形PMON的面积S=PM∙PN=|y|∙|x|.,yxk=∴||kSkxy==,。
这就说明,过双曲线上任意一点作x轴、y轴的垂线,所得到的矩形的面积为常数|k|。
这是系数k几何意义,明确了k的几何意义,会给解题带来许多方便。
(请学生思考,图中三角形OEF的面积和系数k的关系。
)2.反比例函数的图象在用描点法画反比例函数y=kx的图象时,应注意自变量x的取值不能为0,应从1或-1开始对称取点.例题1函数y=1x-(x>0)的图象大致是( )例题2 函数y=kx+1与函数y=kx在同一坐标系中的大致图象是( )yOxAyO xByOxCyOxD y y y y3.反比例函数y=kx 中k 的意义注意:反比例函数y=k x (k ≠0)中比例系数k 的几何意义,即过双曲线y=kx(k ≠0)上任意一点引x 轴、y 轴垂线,所得矩形面积为│k │.例题1:如图,P 、C 是函数x4y =(x>0)图像上的任意两点,过点P 作x 轴的垂线PA,垂足为A ,过点C 作x 轴的垂线CD,垂足为D ,连接OC 交PA 于点E ,设⊿POA 的面积为S1,则S1= ,梯形CEAD 的面积为S2,则S1与S2的大小关系是S1 S2, ⊿POE 的面积S3和梯形CEAD 的面积为S2的大小关系是S2 S3.例题1图 例题2图 例题3图例题2:如图所示,直线l 与双曲线)0(ky >=k x交A 、B 两点,P 是AB 上的点,试比较⊿AOC 的面积S1,⊿BOD 的面积S2,⊿POE 的面积S3的大小: 。
例题3:如图所示,点A(x1,y1)、B(x2,y2)都在双曲线)0x (k>=xy 上,且x2-x1=4,y1-y2=2;分别过点A 、B 向x 轴、y 轴作垂线,垂足分别为C 、D 、E 、F ,AC 与BF 相交于G 点,四边形FOCG 的面积为2,五边形AEODB 的面积为14,那么双曲线的解析式为 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
反比例函数比例系数k的几何意义
反比例函数y= k/x (k≠0)中比例系数k的几何意义,即过双曲线y=k/x (k≠0)上任意一点引x轴、y轴垂线
,所得矩形面积为│k│
1、如图,反比例函数4
y
x
=-的图象与直线
1
3
y
x
=-的交点为A,B,过点A作y轴的平行线与过点B作x轴的平行线相交于点C,则ABC
△的面积为()
6
2、如图,点A是y轴正半轴上的一个定点,点B是反比例函数y=
2
x(x>0)图象上的一个动点,当点B的纵坐标逐渐减小时,△OAB的面积将()A.逐渐增大B.逐渐减小C.不变D.先增大后减小
3、如图12,A、B是函数2
y
x
=
的图象上关于原点对称的任意两点,BC∥x轴,AC∥y 轴,△ABC的面积记为S,则()
A.2
S=D.4
S>
第3题
第5题图第6题图
第12题
4、如图,已知双曲线)0k (x
k y >=经过直角三角形OAB 斜边OB 的中点D ,与直角
边AB 相交于点C .若△OBC 的面积为3,则k =____________.
5、如图5所示,P 1(x 1,y 1)、P 2(x 2,y 2),……P n (x n ,y n )在函数y=x
9
(x >0)的图象上,△OP 1A 1,△P 2A 1A 2,△P 3A 2A 3……△P n A n -1A n ……都是等腰直角三角形,斜边OA 1,A 1A 2……A n-1A n ,都在x 轴上,则y 1+y 2+…y n = 。
6、如图,已知点A 、B 在双曲线x
k y =(x >0)上,AC ⊥x 轴于点C ,BD ⊥y 轴于
点D ,AC 与BD 交于点P ,P 是AC 的中点,若△ABP 的面积为3,则k = .
7、如图,在第一象限内,点P (2,3),M ()2,a 是双曲线)0(≠=k x
k
y 上的两点,PA
⊥x 轴于点A,MB ⊥x 轴于点B,PA 与OM 交于点C,则△OAC 的面积为 8、如图,若正方形OABC 的顶点B 和正方形ADEF 的顶点E 都在函数 1y x
=(0x >)的图象上,则点E 的坐标是( , ).
9、如图,点A 、B 是双曲线3y x
=上的点,分别经过A 、B 两点向x 轴、y 轴作垂
线段,若1S =阴影,则1
2S
S +=
.
第8题图
9题图
10、如图,已知双曲线(0)k y k x
=<经过直角三角形OAB 斜边OA 的中点D ,且与
直角边AB 相交于点C .若点A 的坐标为(6-,4),则△AOC 的面积为 ( ) A .12 B .9 C .6 D .4
11、如图,A 是反比例函数图象上一点,过点A 作AB ⊥y 轴于点B ,点P 在x 轴
上,△ABP 的面积为2,则这个反比例函数的解析式为______________.
12、如图,已知在直角梯形AOBC 中,AC ∥OB ,CB ⊥OB ,OB =18,BC =12,
AC =9,对角线OC 、AB 交于点D ,点E 、F 、G 分别是CD 、BD 、BC 的中点.以O 为原点,直线OB 为x 轴建立平面直角坐标系,则G 、E 、D 、F 四个点中与点A 在同一反比例函数图象上的是(A )
A .点G
B .点E
C .点
D D .点F
13、已知点A 在双曲线y=6
x
上,且OA=4,过A 作AC ⊥x 轴于C ,OA 的垂直平
分线交OC 于B .(1)则△AOC 的面积= ,(2)△ABC 的周长为 14、如图,一次函数y ax b =+的图象与x 轴,y 轴交于A ,B 两点,与反比例函数
k
y x
=
的图象相交于C ,D 两点,分别过C ,D 两点作y 轴,x 轴的垂线,垂足为E ,F ,连接CF ,DE .有下列四个结论:
①△CEF 与△DEF 的面积相等; ②△AOB ∽△FOE ; ③△DCE ≌△CDF ; ④AC BD =.
其中正确的结论是 .(把你认为正确结论的序号都填上)
(第11题)。
