测量平差 第三章习题与答案
测量平差习题集

第二部分 自测题第一章 自测题一、判断题(每题2分,共20分)1、 通过平差可以消除误差,从而消除观测值之间的矛盾。
( )2、 观测值i L 与其偶然真误差i ∆必定等精度。
( )3、 测量条件相同,观测值的精度相同,它们的中误差、真误差也相同。
( )4、 或然误差为最或然值与观测值之差。
( )5、 若X 、Y 向量的维数相同,则YX XY Q Q =。
( )6、 最小二乘原理要求观测值必须服从正态分布。
( )7、 若真误差向量的数学期望为0,即0=∆)(E ,则表示观测值中仅含偶然误差。
( ) 8、 单位权中误差变化,但权比及中误差均不变。
( ) 9、 权或权倒数可以有单位。
( )10、相关观测值权逆阵Q 的对角线元素ii Q 与权阵P 的对角线元素ii P 之间的关系为1=ii ii P Q 。
( )二、填空题(每空0.5分,共20分)1、测量平差就是在 基础上,依据 原则,对观测值进行合理的调整,即分别给以适当的 ,使矛盾消除,从而得到一组最可靠的结果,并进行 。
2、测量条件包括 、 、 和 ,由于测量条件的不可能绝对理想,使得一切测量结果必然含有 。
3、测量误差定义为 ,按其性质可分为 、 和 。
经典测量平差主要研究的是 误差。
4、偶然误差服从 分布,它的概率特性为 、 和 。
仅含偶然误差的观测值线性函数服从 分布。
5、最优估计量应具有的性质为 、 和 。
若模型为线性模型,则所得最优估计量称为 ,最优估计量主要针对观测值中仅含 误差而言。
要证明某估计量为最优估计量,只需证明其满足 性和 性即可。
6、限差是 的最大误差限,它的概率依据是 ,测量上常用于制定 的误差限。
7、若已知观测值向量L 或其偶然真误差向量∆的协方差阵为∑,则L 或∆的权阵定义为L P =∆P = ,由于验前精度∑难以精确求得,实用中定权公式有 、 、 ,特别是对独立等精度观测向量L 而言,其权阵可简单取为L P = 。
误差理论与测量平差基础第三章 协方差传播律及权

X
0 1
,
X
0 2
,
,
X
0 n
也可写为:
dZ
f X1
dX1 0
f X
2
dX2 0
f X
n
0 dX n
KdX
因此只要对非线性函数求全微分,获得系数矩阵即 可应用协方差传播率
12
第三章 协方差传播率及权
6、多个观测向量非线性函数的方差—协方差矩阵
基本思想:a、利用泰勒级数展开,略去二次以上项,
为第l2ilj i组E观(li测 值E(l的i ))方(l j 差 E;(l j ))
为第i组观测值关于第j组观测值的协方差,协方差用 来描述第i个观测值与第j个观测值之间的相关程度。
3
第三章 协方差传播率及权
§3-2 协方差传播率
1、协方差传播律的作用 (图3-1示例)
计算观测向量函数的方差—协方差矩阵,从而评 定观测向量函数的精度。
20
第三章 协方差传播率及权
对上式求全微分,得
dZ1
f1 X 1
dX 1
f1 X 2
dX 2
f1 X n
dX n
dZ 2
f 2 X 1
dX 1
f 2 X 2
dX 2
f 2 X n
dX n
dZt
f t X 1
dX 1
f t X 2
dX 2
f t X n
dX n
21
第三章 协方差传播率及权
2、预备公式
E(C) C , E(CX ) CE(X ), E(X Y ) E(X ) E(Y )
E(X1 X 2 X n ) E(X1) E(X 2) E(X n )
测量平差所有习题
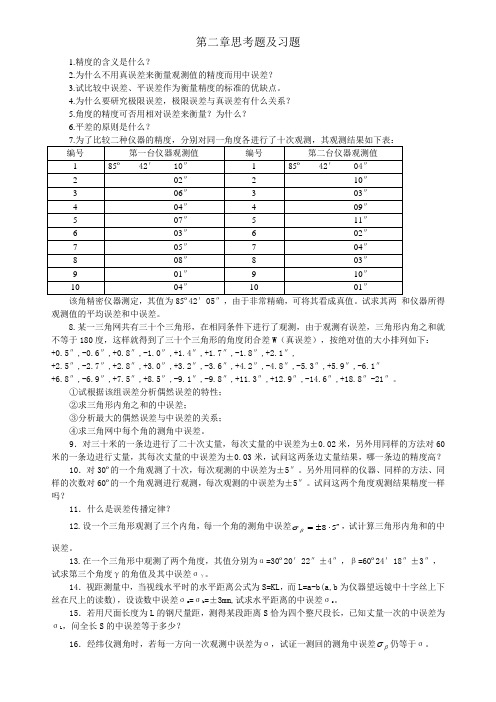
第二章思考题及习题1.精度的含义是什么?2.为什么不用真误差来衡量观测值的精度而用中误差?3.试比较中误差、平误差作为衡量精度的标准的优缺点。
4.为什么要研究极限误差,极限误差与真误差有什么关系?5.角度的精度可否用相对误差来衡量?为什么?6.平差的原则是什么?观测值的平均误差和中误差。
8.某一三角网共有三十个三角形,在相同条件下进行了观测,由于观测有误差,三角形内角之和就不等于180度,这样就得到了三十个三角形的角度闭合差W(真误差),按绝对值的大小排列如下:+0.5″,-0.6″,+0.8″,-1.0″,+1.4″,+1.7″,-1.8″,+2.1″,+2.5″,-2.7″,+2.8″,+3.0″,+3.2″,-3.6″,+4.2″,-4.8″,-5.3″,+5.9″,-6.1″+6.8″,-6.9″,+7.5″,+8.5″,-9.1″,-9.8″,+11.3″,+12.9″,-14.6″,+18.8″-21″。
①试根据该组误差分析偶然误差的特性;②求三角形内角之和的中误差;③分析最大的偶然误差与中误差的关系;④求三角网中每个角的测角中误差。
9.对三十米的一条边进行了二十次丈量,每次丈量的中误差为±0.02米,另外用同样的方法对60米的一条边进行丈量,其每次丈量的中误差为±0.03米,试问这两条边丈量结果,哪一条边的精度高?10.对30º的一个角观测了十次,每次观测的中误差为±5″。
另外用同样的仪器、同样的方法、同样的次数对60º的一个角观测进行观测,每次观测的中误差为±5″。
试问这两个角度观测结果精度一样吗?11.什么是误差传播定律?12.设一个三角形观测了三个内角,每一个角的测角中误差58''⋅±=βσ,试计算三角形内角和的中误差。
13.在一个三角形中观测了两个角度,其值分别为α=30º20′22″±4″,β=60º24′18″±3″,试求第三个角度γ的角值及其中误差σγ。
测量平差第三章习题与答案

测量平差第三章思考题3.1 下列各式中的()1,2,3i L i =均为等精度独立观测值,其中误差为s ,试求X 的中误差: (1)()12312X LL L =++;(2)123L L X L =3.2 已知观测值1L ,2L 的中误差12s s s ==,120s =,设11225,2X L Y L L =+=-,12Z L L =,t X Y =+,试求X ,Y ,Z 和t 的中误差。
的中误差。
3.3 设有观测向量[]12331TL L L L =,其协方差阵为,其协方差阵为40003002L LD éùêú=êúêúëû分别求下列函数的的方差:分别求下列函数的的方差: (1)1133F L L =-; (2)2233F L L =3.4 设有同精度独立观测值向量[]12331TL LLL=的函数为113s i n s i n A BL Y S L =,22A B Y L a =-,式中A B a 和A B S 为无误差的已知值,测角误差1"s =,试求函数的方差12y s 、22y s及其协方差12y y s3.5 在图中△ABC 中测得A A s б,边长b b s ±,c c s ±,试求三角形面积的中误差ss 。
3.6 在水准测量中,设每站观测高差的中误差均为1mm ,今要求从已知点推算待定点的高程中误差不大于5cm ,问可以设多少站?,问可以设多少站? 3.7 有一角度测4个测回,得中误差为0.42〃,问再增加多少个测回其中误差为0.28〃?〃? 3.8 在相同观测条件下,应用水准测量测定了三角点A ,B ,C 之间的高差,设三角形的边长分别为S 1=10km ,S 2=8km ,S 3=4km ,令40km 的高差观测值权威单位权观测,试求各段观测高差之权及单位权中误差。
《测量平差》学习辅导

《测量平差》学习辅导第一章测量平差及其传播定律一、学习要点(一)内容:测量误差的概念、测量误差来源、分类;偶然误差概率特性;各种精度指标;真误差定义;协方差传播律;权与定权的常用方法;协因数传播律;权逆阵及其传播规律。
(二)基本要求:1.了解测量平差研究的对象和内容;2.掌握偶然误差的四个概率特性;3.了解精度指标与误差传播偶然误差的规律;4.了解权的定义与常用的定权方法;5.掌握协方差传播率。
(三)重点:偶然误差的规律性,协方差、协因数的概念、传播律及应用;权的概念及定权的常用方法。
(四)难点:协方差、协因数传播率二、复习题(一)名词解释1.偶然误差2.系统误差3.精度4.单位权中误差(二)问答题1.偶然误差有哪几个概率特性?2.权是怎样定义的,常用的定权方法有哪些?(三)计算题σ的量测中误差1.在1:500的图上,量得某两点间的距离d=23.4mm,dσ。
σ=±0.2mm,求该两点实地距离S及中误差s三、复习题参考答案 (一)名词解释1.偶然误差:在一定条件下做一系列的观测,如果观测误差从表面上看其数值和符号不存在任何确定的规律性,但就大量误差总体而言,具有统计性的规律,这种误差称为偶然误差。
2.系统误差:在一定条件下做一系列的观测,如果观测的误差在大小、符号上表现出系统性,或者为某一常数,或者按照一定的规律变化,这种带有系统性和方向性的误差称为系统误差。
3.精度:表示同一量的重复观测值之间密集或吻合的程度,即各种观测结果与其中数的接近程度。
4.单位权中误差:权等于1的中误差称为单位权中误差。
(二)问答题1.答:有四个概率特性:①在一定观测条件下,误差的绝对值有一定的限值,或者说超出一定限值的误差出现的概率为零;②绝对值较小的误差比绝对值较大的误差出现的概率大;③绝对值相等的正负误差出现的概率相同;④偶然误差的数学期望为零。
2.答:设i L (i=1,2,3,…,n ),他们的方差为2i σ,如选定任一常数0σ,则定义:22ip σσ=,称为观测值L i 的权。
测量平差课后练习题(1~3章)2011

《误差理论与测量平差基础》课后测验题第一章 绪论1、什么是观测条件?相同观测条件下进行的观测称为什么观测?2、举出系统误差和偶然误差的例子各5个。
3、观测误差分为几类?分别是如何定义的?4、在测量上为什么要进行多余观测?5、测量平差的任务是什么?第二章 误差分布与精度指标1、什么是真值、真误差?2、简述偶然误差的特性?3、偶然误差服从什么分布?4、衡量精度的指标有哪几种?分别是如何定义的?5、设一段距离为:520m ±2.3mm 代表什么意思?相对误差是多少?6、对于在相同的观测条件下进行的一系列的观测,误差有大有小,是否代表精度不同?7、在测距仪的检定中,要对基线场两固定观测墩点间的精确距离进行多次观测,设精确距离为326.750米,观测了10次,得距离如下:326.758m 326.754m 326.745m 326.755m 326.762m326.749m 326.743m 326.740m 326.751m 326.756m求测量距离的中误差?8、在采用J6经纬仪进行角度测量时,规定半测回角值之差不超过36",测回间角值之差不超过24",分别代表什么误差?9、什么是协方差?协方差是描述观测值之间什么关系的?10、在什么情况下,观测值之间相互独立与不相关是等价的?11、什么是方差协方差阵?其是有什么组成的?有何特点?12、何谓准确度?何谓精确度?何谓不确定性?第三章 协方差传播率及其权1、设观测向量T L L L L ]3,2,1[=的方差协方差阵为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=411121113LLD ,求21L σ、22L σ、21L L σ。
2、写出协方差传播律的主要公式?3、当观测值的函数为非线性时,如何处理?4、简述协方差传播律的应用步骤?5、 已知独立观测值2,1L L 的中误差分别为1L σ、2L σ,求下列函数的中误差:(1)2513L L y +=(2)21L L y =6、设观测向量T L L L L ]3,2,1[=的方差协方差阵为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=411121113LL D , 求(1)325131L L L y ++=(2)212L L y -=的1y σ、2y σ、21y y σ、21L y σ7、已知随机变量y 、z 都是观测值L=[L1、L2、L3]T 的函数,函数关系如下:3162101733241L L L z L L L y +-=++=,已知⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=420231012D ,证明y 、z 间互不相关。
误差理论与测量平差(山东联盟)智慧树知到答案章节测试2023年山东建筑大学

第一章测试1.误差是不可避免的。
A:对B:错答案:A2.构成观测条件的要素有哪些A:外界条件B:计算工具C:观测者D:测量仪器答案:ACD3.对中误差属于那种误差A:系统误差B:偶然误差C:不是误差D:粗差答案:B第二章测试1.两随机变量的协方差等于0时,说明这两个随机变量A:相关B:互不相关C:相互独立答案:B2.观测量的数学期望就是它的真值A:错B:对答案:A3.衡量系统误差大小的指标为A:精确度B:准确度C:不确定度D:精度答案:B4.精度是指误差分布的密集或离散程度,即离散度的大小。
A:错B:对答案:B5.若两观测值的中误差相同,则它们的A:测量仪器相同B:真误差相同C:观测值相同D:精度相同答案:D第三章测试1.设L的权为1,则乘积4L的权P=()。
A:1/4B:4C:1/16D:16答案:C2.有一角度测20测回,得中误差±0.42秒,如果要使其中误差为±0.28秒,则还需增加的测回数N=()。
A:25B:45C:20D:5答案:A3.在水准测量中,设每站观测高差的中误差均为1cm,今要求从已知点推算待定点的高程中误差不大于5cm,问可以设25站。
A:对B:错答案:A4.已知距离AB=100m,丈量一次的权为2,丈量4次平均值的中误差为2cm,若以同样的精度丈量CD的距离16次,CD=400m,则两距离丈量结果的相对中误差分别为( 1/5000 )、(1/20000 )。
A:错B:对答案:B5.A:29B:35C:5D:25答案:D第四章测试1.当观测值为正态随机变量时,最小二乘估计可由最大似然估计导出。
A:对B:错答案:A2.多余观测产生的平差数学模型,都不可能直接获得唯一解。
A:对B:错答案:A3.在平差函数模型中,n、t、r、u、s、c等字母各代表什么量?它们之间有何关系?( n观测值的个数 )(t必要观测数 )(r多余观测数,r=n-t )(u所选参数的个数 )( s非独立参数的个数,s=u-t )( c所列方程的个数,c=r+u )A:对B:错答案:A4.A:对B:错答案:A5.A:错B:对答案:B第五章测试1.关于条件平差中条件方程的说法正确的是:A: 这r个条件方程应彼此线性无关B: 应列出r个条件方程C: r个线性无关的条件方程必定是唯一确定的,不可能有其它组合。
(整理)测量平差习题集

第二部分 自测题第一章 自测题一、判断题(每题2分,共20分)1、 通过平差可以消除误差,从而消除观测值之间的矛盾。
( )2、 观测值i L 与其偶然真误差i ∆必定等精度。
( )3、 测量条件相同,观测值的精度相同,它们的中误差、真误差也相同。
( )4、 或然误差为最或然值与观测值之差。
( )5、 若X 、Y 向量的维数相同,则YX XY Q Q =。
( )6、 最小二乘原理要求观测值必须服从正态分布。
( )7、 若真误差向量的数学期望为0,即0=∆)(E ,则表示观测值中仅含偶然误差。
( ) 8、 单位权中误差变化,但权比及中误差均不变。
( ) 9、 权或权倒数可以有单位。
( )10、相关观测值权逆阵Q 的对角线元素ii Q 与权阵P 的对角线元素ii P 之间的关系为1=ii ii P Q 。
( )二、填空题(每空0.5分,共20分)1、测量平差就是在 基础上,依据 原则,对观测值进行合理的调整,即分别给以适当的 ,使矛盾消除,从而得到一组最可靠的结果,并进行 。
2、测量条件包括 、 、 和 ,由于测量条件的不可能绝对理想,使得一切测量结果必然含有 。
3、测量误差定义为 ,按其性质可分为 、 和 。
经典测量平差主要研究的是 误差。
4、偶然误差服从 分布,它的概率特性为 、 和 。
仅含偶然误差的观测值线性函数服从 分布。
5、最优估计量应具有的性质为 、 和 。
若模型为线性模型,则所得最优估计量称为 ,最优估计量主要针对观测值中仅含 误差而言。
要证明某估计量为最优估计量,只需证明其满足 性和 性即可。
6、限差是 的最大误差限,它的概率依据是 ,测量上常用于制定 的误差限。
7、若已知观测值向量L 或其偶然真误差向量∆的协方差阵为∑,则L 或∆的权阵定义为L P =∆P = ,由于验前精度∑难以精确求得,实用中定权公式有 、 、,特别是对独立等精度观测向量L 而言,其权阵可简单取为L P = 。
8、已知真误差向量1⨯∆n 及其权阵P ,则单位权中误差公式为 ,当权阵P 为 此公式变为中误差公式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
测量平差第三章思考题
3.1 下列各式中的()1,2,3i L i =均为等精度独立观测值,其中误差为σ,试求X 的中误差: (1)()12312
X L L L =++;
(2)12
3
L L X L =
3.2 已知观测值1L ,2L 的中误差12σσσ==,120σ=,设11225,2X L Y L L =+=-,
12Z L L =,t X Y =+,试求X ,Y ,Z 和t 的中误差。
3.3 设有观测向量[]1
2
331
T
L L L L =,其协方差阵为
4
000300
2LL
D ⎡⎤
⎢⎥=⎢⎥⎢⎥⎣⎦
分别求下列函数的的方差: (1)1133F L L =-; (2)2233F L L =
3.4 设有同精度独立观测值向量[]1
2
3
31
T
L L L
L
=的函数为113
s i n s i n AB
L Y S L =,
22AB Y L α=-,式中A B α和AB S 为无误差的已知值,测角误差1"σ=,试求函数的方差1
2
y σ、
2
2
y σ
及其协方差12
y y σ
3.5 在图中△ABC 中测得A A σ∠±,边长b b σ±,c c σ±,试求三角形面积的中误差s σ。
3.6 在水准测量中,设每站观测高差的中误差均为1mm ,今要求从已知点推算待定点的高程中误差不大于5cm ,问可以设多少站?
3.7 有一角度测4个测回,得中误差为0.42〃,问再增加多少个测回其中误差为0.28〃? 3.8 在相同观测条件下,应用水准测量测定了三角点A ,B ,C 之间的高差,设三角形的边
长分别为S 1=10km ,S 2=8km ,S 3=4km ,令40km 的高差观测值权威单位权观测,试求各段观测高差之权及单位权中误差。
3.9 以相同观测精度A ∠和B ∠,其权分别为14
A P =,12
B P =,已知8"B σ=,试求单位
权中误差0A σ∠和的中误差A σ。
3.10 已知观测值向量21L 的权阵为522
4LL P -⎡⎤
=⎢
⎥-⎣⎦
,试求观测值的权1L P 和2L P
答案:
3.1 (1)x σ=
, (2)3
x L
σ=
3.2 2x σσ=,y σ=,z σ=
,t σ=
3.3 1
22F D =,22
2
231827F D L L =+
3.4 ()1
222
2
2
113"2
2
3
cos
sin cot sin AB y S
L L L L σ
ρ
=
+⋅
()222
1y σ=秒
12
0y y σ
=
3.5 s σ=
3.6 最多可设25站 3.7 再增加5个测回
3.8 1
4.0P =,2
5.0P =,310.0P =,0()km σ=
3.9 "0 5.66σ=,"
11.31A σ=
3.10 1
4L P =,2
165
L P =。
