4.3二维正态分布
概率论与数理统计正态分布4-3二维正态分布课件

统计决策
基于二维正态分布,可以制定统 计决策规则,例如置信区间和预 测区间的确定。
在金融领域的应用
1 2 3
资产定价
二维正态分布可以用于资产定价模型,如期权定 价模型,以模拟两个相关资产的价格变动。
风险管理
在金融领域,二维正态分布可用于评估投资组合 的风险,例如计算投资组合的VaR值(风险价 值)。
例如,对于二维正态分布的均值向量,可以通过样本数据的均值向量进行检验, 判断其与理论值是否存在显著差异。
非参数检验
非参数检验是在总体分布形式未知或认为总体分布形式与理论分布形式存在较大差异的情况下,利用 样本数据对总体分布进行检验的方法。在二维正态分布的情境下,非参数检验通常包括核密度估计、 散点图和多维距离等方法。
特性
分布函数具有连续性、非负性和归一性等特性,能够完整描述随机向量的概率 分布。
03
二维正态分布的应用
在统计学中的应用
参数估计
二维正态分布可以用于估计两个 变量的联合概率分布,从而对参 数进行估计,如线性回归中的参 数估计。
假设检验
在统计分析中,二维正态分布可 以用于检验两个变量之间是否存 在某种关系,例如相关性检验或 因果关系检验。
金融数据分析
二维正态分布可以用于分析金融数据,例如股票 价格和交易量的关系。
在物理和工领域的应用
信号处理
在通信和雷达信号处理中,二维正态分布可用于 描述信号的功率谱密度。
地震学
在地震学中,二维正态分布可用于描述地震事件 的时空分布。
图像处理
在图像处理中,二维正态分布可用于描述图像的 像素强度分布。
边缘分布的特性
总结词
边缘分布是指将二维正态分布的其中一个随机变量固定,得到的另一个随机变量 的分布。
概率论与数理统计正态分布4-3 二维正态分布课件
概率论与数理统计教程(第五版)
目录
上一页
下一页
返回
结束
§4.3 二维正态分布
2 2 设 ( X , Y ) ~ N ( , , , [定理3] x y x y , r) , 则 X 与 Y 独立的充要条件是 r 0.
证: 必要性:若随机变量 X 与Y 相互 独立, 则r 0 . 充分性:若 r 0 , 则二维正态分布的联合密度可化为:
I ( x) y2
r( x x )
y (1 r ) t e
t 2 2
dt
r y ( x x )
x
]e
t 2 2
dt
x
1 r
2
e
t 2 2
dt
r y ( x x )
所以
概率论与数理统计教程(第五版)
目录
上一页
下一页
返回
结束
§4.3 二维正态分布
y y r( x x ) ( x x ) 1 , 2 2 2 x 2(1 r ) y x
2
2
y y r( x x ) 1 [ ], 则 设t 2 y x 1 r
f ( x , y ) 2 π x y e
1
2 2 [ ( x x ) 2 x ( y y ) 2 y ] 2
1 2 π x
e ( x x )
2
2 ( 2 x )
1 2 π y
e
2 ( y y )2 ( 2 y )
f X ( x ) fY ( y ) . 所以,随机变量 X 与 Y相互独立.
x x
二维正态分布的条件期望

二维正态分布的条件期望
二维正态分布既简称又称“高斯分布”,它是一种在数学统计学中最为常见的多维概率分布类型,是概率论和统计学中重要的概念。
根据它可以更好地了解和描述各种事件发生的概率状况。
一般情况下,二维正态分布的条件期望和其概率密度函数具有一定的对称性,即条件期望点在坐标原点,概率在其任何方向上都有相同的概率。
另外,条件期望的曲线的横轴和纵轴的均值和标准偏差也有一定的规律,如二维正态分布图像中,可以看到,其条件期望的曲线向外伸展,随着离坐标原点越远,范围越大,概率密度函数越低,反之越小。
此外,二维正态分布的条件期望和其概率密度函数还可以用来估算二维随机变量,例如处可以用来正态分布推断不同空间中随机变量的期望值,分析其概率以及在不同随机变量取值的概率状况,从而用来分析和推断遇到的不同问题。
总的来说,二维正态分布的条件期望具有一定的对称性,常用来估算二维随机变量的期望值,以及其概率状况,可应用于推断和分析多种不同问题,从而更好地解决实际问题。
概率论与数理统计正态分布4-3二维正态分布课件

二维正态分布的应用场景
金融领域
在金融领域中,二维正态分布常 用于描述股票价格或其他金融变 量的联合分布,帮助投资者进行 风险评估和投资组合优化。
自然学科
在物理、化学、生物等自然学科 中,二维正态分布可用于描述实 验数据的误差分布、气象数据的 联合概率分布等。
概率论与数理统计正态分 布4-3二维正态分布课件源自目录CONTENTS
• 二维正态分布概述 • 4-3二维正态分布特性 • 4-3二维正态分布的性质 • 4-3二维正态分布的统计推断 • 4-3二维正态分布的实际应用
01 二维正态分布概述
二维正态分布的定义
二维正态分布是概率论与数理统计中 一种重要的概率分布,描述了两个随 机变量之间相互独立且具有相同的正 态分布关系。
03
4-3二维正态分布描述了两个随机变量之间线性关系 的情况。
4-3二维正态分布的数学表达式
1
4-3二维正态分布的数学表达式为f(x1, x2) = (1 / (2πσ1σ2)) * exp(-((x1-μ1)^2/2σ1^2 + (x2μ2)^2/2σ2^2))。
2
该表达式描述了两个随机变量x1和x2的概率密度 函数,其中μ1, μ2, σ1^2 和σ2^2是常数。
方差齐性检验
通过检验各组数据的方差是否相等,判断数据是 否满足方差分析的前提条件。
方差分析表
列出各组数据的均值、方差、自由度和贡献度等 信息,用于比较不同组之间的差异。
05 4-3二维正态分布的实际 应用
在金融领域的应用
资产定价
二维正态分布可以用于资产定价模型,例如Black-Scholes模型, 以评估衍生品的价值。
概率论与数理统计 第四节 二维正态分布
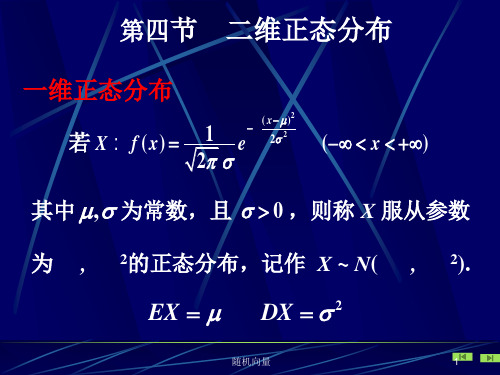
可得 X N ( 1 , 12 ) , Y N ( 2 , 2 2 ) .
证
f X ( x)
1
f ( x , y )dy
2 1 2 1 2
x 1 y 2 y 2 2 x 1 2 1 exp ( ) 2 ( )( )( ) dy 2 1 2 2 2(1 ) 1
1 2 1 1 2
令
y 2
2
t
x 1 x 1 2 2 1 exp ( ) 2 ( ) t t dt 2 1 2(1 ) 1
1 2 1 1 2
x 1 x 1 2 2 1 exp ( ) 2 ( ) t t dt 2 1 2(1 ) 1
XZ 0
2 3.设( X , Y ) N ( 1 , 2 , 12 , 2 , ),则X 与Y 的非零
线性组合 aX bY 仍服从正态分布,且
2 aX bY N (a 1 b2 , a 2 12 b 2 2 2ab 1 2 )
随机向量
6
( x 1 )2 x 1 2 1 1 exp ( t ) dt exp 2 2 1 2 1 2 1 1 2 2(1 ) x 1 t 2 ( x 1 ) 1 2 1 exp exp 1 ( ) dt 2 2 1 2 2 1 1 2 1 2 x 1 t 2 ( x 1 )2 1 u )du (令 1 exp ( u) exp 2 2 2 2 1 2 1 1
二维标准正态分布函数

二维标准正态分布函数二维标准正态分布函数是描述两个随机变量之间关系的概率分布函数。
在统计学和概率论中,它是一种重要的分布函数,用来描述两个变量之间的相关性和概率分布情况。
本文将对二维标准正态分布函数进行详细介绍,包括定义、性质、应用等方面的内容。
首先,我们来看一下二维标准正态分布函数的定义。
二维标准正态分布函数是指两个独立的标准正态分布随机变量X和Y的联合分布函数。
其概率密度函数可以表示为:f(x, y) = 1/(2π) exp((x^2 + y^2)/2)。
其中,x和y分别是两个随机变量的取值,exp表示自然指数函数。
这个函数描述了两个随机变量的联合概率分布情况,可以用来计算两个变量之间的相关性和概率分布。
其次,我们来看一下二维标准正态分布函数的性质。
二维标准正态分布函数具有以下几个重要的性质:1. 对称性,二维标准正态分布函数关于原点对称,即f(x, y) = f(-x, -y)。
这说明在二维标准正态分布中,概率密度在原点处取得最大值,随着距离原点的增加而逐渐减小。
2. 独立性,如果两个随机变量X和Y是相互独立的标准正态分布,那么它们的联合分布就是二维标准正态分布函数。
这个性质在实际应用中非常重要,可以帮助我们理解和分析两个变量之间的关系。
3. 边缘分布,二维标准正态分布函数的边缘分布是两个独立的标准正态分布。
这意味着我们可以通过二维标准正态分布函数来推导出每个变量的边缘分布,从而更好地理解每个变量的特性。
最后,我们来看一下二维标准正态分布函数的应用。
二维标准正态分布函数在统计学、金融学、工程学等领域都有重要的应用,例如:1. 统计推断,在统计学中,我们经常需要分析两个变量之间的相关性和概率分布情况,二维标准正态分布函数可以帮助我们进行相关性分析和概率计算。
2. 金融建模,在金融学中,我们经常需要对多个随机变量进行建模和分析,二维标准正态分布函数可以作为建模工具,帮助我们理解和预测金融市场的波动情况。
二维标准正态分布
二维标准正态分布二维标准正态分布是统计学中一个重要的概念,它描述了两个随机变量同时服从标准正态分布的情况。
在实际应用中,我们经常会遇到多个变量之间的相关性,而二维标准正态分布可以帮助我们更好地理解和分析这种相关性。
本文将对二维标准正态分布的概念、性质和应用进行详细介绍。
首先,二维标准正态分布可以用一个二维平面上的曲线来表示,这个曲线呈椭圆形状,中心位于坐标轴的交点处。
椭圆的长短轴和方向与两个变量的相关性有关,相关性越强,椭圆越扁,相关性越弱,椭圆越圆。
通过观察这个椭圆,我们可以直观地了解两个变量之间的相关性强弱。
其次,二维标准正态分布的密度函数可以用数学公式来表示,其数学表达式为:f(x, y) = 1/(2π) e^(-1/2 (x^2 + y^2))。
其中,x和y分别代表两个变量的取值,e为自然对数的底。
这个数学公式描述了二维标准正态分布在不同取值下的概率密度,通过对这个函数的分析,我们可以得到关于两个变量的各种统计特征,比如均值、方差、协方差等。
另外,二维标准正态分布还有一些重要的性质,比如两个变量的线性组合仍然服从正态分布,这对于一些统计推断和模型拟合有着重要的应用。
此外,二维标准正态分布还与多元正态分布有着密切的联系,多元正态分布是指多个变量同时服从正态分布的情况,而二维标准正态分布可以看作是多元正态分布的特例。
在实际应用中,二维标准正态分布可以帮助我们分析和建模多个变量之间的相关性。
比如在金融领域,我们可以利用二维标准正态分布来描述股票收益率之间的相关性,从而进行风险管理和资产配置。
在生物统计学中,我们可以利用二维标准正态分布来研究两个生物特征之间的相关性,从而推断它们之间的遗传关系和生理机制。
总之,二维标准正态分布是统计学中一个重要的概念,它可以帮助我们更好地理解和分析多个变量之间的相关性。
通过对二维标准正态分布的认识,我们可以在实际问题中更加准确地进行统计推断和建模分析,为决策提供更可靠的依据。
4-3二维正态分布
密度函数, 法1求出Z密度函数,直接随机变量期望的定义 求出 密度函数 求期望和方差. 在例1中求得了Z 求期望和方差 在例1中求得了Z的概率密度
因此由随机变量的期望定义 E(X) = ∫−∞ x f (x)dx 可得
1 e , z >0 fZ (z) = 2 0, z ≤0 ≤0
z − 2
I (x)dx
得到
+∞ x − µ r x R(X,Y) = ∫−∞ σx e 2πσx
2
(x−µx )2 − 2 2σx
dx
置换积分变量
R( X,Y) =
x − µx
σx
x
= t 得到
2πσ ∫
r
t2 − +∞ 2 2 −∞
t e dx = r
∫
t2 +∞ − 2 2 −∞ +∞
2 2
2 2
)
1 ⋅ e 2π
x2 +y2 − 2
=∫
+∞ +∞
−∞ −∞
(x +y ) ∫
2
2 2
dxdy
由极坐标变换公式可得
+∞ − 1 2π 5 E( Z ) = ∫ dθ∫ ρ ⋅ e 2 dρ 0 2π 0 2
ρ2
置换积分变量
2
ρ
2
2
= t, ρ = 2t, 可得
2 +∞ t2 − 2
−∞
=
rσy (x −µx )
σx
−∞
σx
rσy (x − µx )
1−r
t2 +∞ − 2 2 −∞
∫
e dt
=
σx
二维正态分布.ppt
数学与信息技术系
定义 设二维连续随机变量(X,Y)的联合概率密度为
f (x, y)
1
2 x y 1 r2
2
1 (1
r
2
)
(
x
x
2 x
)2
2
r
(
xx
)( y x y
y
)
(
y
y
2 y
)2
e 其中 x , y , x 0, y 0, r r 1 是分布参数
这种分布叫做二维正态分布。
x
)
t,得到
I(x) y1 r2来自t1r2
r(x x) x
t2 e 2 dt
y 1 r2
te
t2 2
dt
r
y
(x
x
)
1 r2
t 2
e 2 dt
x
r y (x x )
1 r2
t 2
e 2 dt
x
r y (x x ) 2 1 r2 x
t2
e 2 dt 2 ,
当z≤0时,显然, FZ(z)=0;当z>0时,
1
x2 y2
FZ (z)
2
e
x2 y2 z
2 dxdy
1
2
d
z
2
e2
d
1
z
e2
2 0
0
所以 Z的分布函数为
FZ
(z)
1
e
z 2
,
z
0
0, z 0
由此Z的概率密度为
fZ
(z)
1 2
e
z 2
,
z
0
二维正态分布.
第14讲二维正态分布中心极限定理教学目的:了解二维正态分布,理解独立同分布的中心极限定理和棣莫佛一拉普拉斯定理。
教学重点:独立同分布的中心极限定理。
教学难点:应用独立同分布的中心极限定理解决实际问题。
教学学时:2学时教学过程:第四章正态分布§ 4.4二维正态分布定义若二维连续随机变量(X,Y)的联合概率密度为f(x,y) ------------- 1. 2e2 x y°1 r21____ [ ( X x )2(1 r2) x22r (x x )( y y) (y 上]2 ]y则称(X,Y)服从二维正态分布,记作(X,Y)~N(;,r) 其中f x(x) f (x, y)dy12 V1 r2ye u(x,y)dy由X 与Y 的对称性可求得Y 的边缘密度为(y y )21 22 —1e 2 y2y由此可见,二维正态分布的两个边缘分布都是正态分布,并且可以知道x E(X), y E(Y), x 、D(X), y ... D(Y)其中1 (xu(x,y)E2r(x x )(y y )(y y )22__ y(xX )2 2 x 22(1宀空 x )] 2设2 .-[亍一]t,则有f x (x)x(x x )2t2-—e 2 x e 2dt 2 x-ex(X 2 x )2-2_ xf Y (y) F 面我们可以看到参数r 为随机变量 X,Y 的相关系数。
RZ 噹;;X ,YL)E{[X E(X)][YE(Y)]}D(X)、D(Y)(xx )(y y )f(x,y)dxdyf x (X)f Y (y).1若随机变量X 与丫相互独立,都服从标准正态分布 N(0,1),求随机变量由于X 与丫都服从标准正态分布N(0,1),概率密度分别为x21 e2 , f Y (x)2 . 2 又随机变量X 与丫相互独立,联合概率密度为x 2y 2f(x,y) 2Le^由此得随机变量Z X 2 Y 2的分布函数数Z X 2 Y 2的分布称为自由度为2的2分布21 —2一2(x x )—2~ x(y y )21 2 2 * * *2 y e 7所以,若随机变量(X,Y)服从二维正态分布,则随机变量 X 与丫相互独立的充要条件函数Z X 2 Y 2的概率密度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
证: 必要性:若随机变量 X 与Y 相互 独立, 则r 0 . 充分性:若 r 0 , 则二维正态分布的联合密度可化为:
f ( x , y ) 2 x y e
z 0; z 0.
2 [此分布称为自由度为2的 分布.]
概率论与数理统计教程(第五版)
目录
上一页
下一页
返回
结束
例2 : 求例1中Z的期望和方差.
解:因为X ~ N (0,1), Y ~ N (0,1) 所以由4.2的例1知:
故EX EY 1 ;DX DY 2。
2 2 2 2
1
目录
上一页
下一页
返回
结束
§4.3 二维正态分布
[定理1] 设二维随机变量 ( X , Y )服从二维正分布 2 2 N ( x , y , x , y , r ) , 则 X与Y 的边缘分布都是正态 分布, 且无论参数 r ( r 1) 为何值, 都有 2 2 X ~ N ( x , x ), Y ~ N ( y , y ) . 证明见P177
概率论与数理统计教程(第五版)
目录 上一页 下一页 返回 结束
§4.3 二维正态分布
当 z 0 时, 显然有 FZ ( z ) 0 ; 当 z 0 时, 有 1 ( x 2 y 2 ) 2 FZ ( z ) e dxdy 2 2 2
x y z
1 2
所以, Z 的分布函数
§4.3 二维正态分布
二维正态分布
x 0y 0x 10y 10 0.5
0.015 0.010
概率论与数理统计教程(第五版)
z
0.005 0.000 -10 -5 5 0 10
y
x
0 5 10 -10
-5
2 x x2 1 x x y y y y f(x,y) exp 2 2 2 2 2 2 1 x y x y 2xy 1
概率论与数理统计教程(第五版)
目录
上一页
下一页
返回
结束
§4.3 二维正态分布
2 2 [定理2] 设( X , Y ) ~ N ( x , y , x , y , r ),则
R ( X , Y ) r.
证明见P178
概率论与数理统计教程(第五版)
目录
上一页
下一页
返回
结束
§4.3 二维正态分布
概率论与数理统计教程(第五版)
目录 上一页 下一页 返回 结束
§4.3 二维正态分布
[例1] 设随机变量 X 与 Y 相互独立, 都服从标准正态分
布 N (0 ,1) , 求随机变量函数 Z X 2 Y 2的概率密度 .
解: 因为随机变量 X 与Y 相互独立, 且已知
1 f X ( x) e 2
所以,
x2 2
1 e , fY ( y ) 2
y2 2
,
1 ( x 2 y 2 ) 2 f ( x , y ) f X ( x ) fY ( y ) e . 2 2 2 由分布函数定义, Z X Y 的分布函数为
FZ ( z ) P( Z z ) P( X 2 Y 2 z ) .
0
2
d
z 2 2
0
e
d
1 e z 2 .
1 e z 2 , FZ ( z ) , 0
概率论与数理统计教程(第五版)
目录
z 0; z 0.
上一页 下一页 返回 结束
§4.3 二维正态分布
由此得 Z 的概率密度
1 e z 2 , f Z ( z) 2 , 0
1
2 2 [ ( x x ) 2 x ( y y )2 y ] 2
( x x ) e 2 x 1
2
2 ( 2 x )
2 y
1
e
2 ( y y ) 2 ( 2 y )
f X ( x ) fY ( y ) . 所以,随机变量 X 与 Y相互独立.
于是 EZ E( X Y ) EX EY 2
2 2 2 2
又因为X , Y 独立,所以X 与Y 也独立. 于是DZ D( X 2 Y 2 ) DX 2 DY 2 2 2 4
概率论与数理统计教程(第五版)
目录 上一页 下一页 返回 结束
2
2
§4.3 二维正态分布
概率论与数理统计教程(第五版)
目录
上一页
下一页
返回
结束
§4.3 二维正态分布
[定义] 设二维随机变量( X , Y )的联合概率密度为
f ( x , y)
1 2 x y 1 r
2
e
2 1 ( x x ) 2 2 r ( x x )( y y ) ( y y ) 2 2 2 (1 r 2 ) x y x y
则称二维随机变量( X , Y )服从二维正态分布, 记作
2 2 ~ N ( , , , ( X ,Y ) x y x y , r)
其中 x , y , x 0 , y 0 , r ( r 1)是分布参数.
概率论与数理统计教程(第五版)
目录
上一页
下一页
返回
结束
