关于二维正态分布的一个教学注记
概率论与数理统计正态分布4-3 二维正态分布课件
概率论与数理统计教程(第五版)
目录
上一页
下一页
返回
结束
§4.3 二维正态分布
2 2 设 ( X , Y ) ~ N ( , , , [定理3] x y x y , r) , 则 X 与 Y 独立的充要条件是 r 0.
证: 必要性:若随机变量 X 与Y 相互 独立, 则r 0 . 充分性:若 r 0 , 则二维正态分布的联合密度可化为:
I ( x) y2
r( x x )
y (1 r ) t e
t 2 2
dt
r y ( x x )
x
]e
t 2 2
dt
x
1 r
2
e
t 2 2
dt
r y ( x x )
所以
概率论与数理统计教程(第五版)
目录
上一页
下一页
返回
结束
§4.3 二维正态分布
y y r( x x ) ( x x ) 1 , 2 2 2 x 2(1 r ) y x
2
2
y y r( x x ) 1 [ ], 则 设t 2 y x 1 r
f ( x , y ) 2 π x y e
1
2 2 [ ( x x ) 2 x ( y y ) 2 y ] 2
1 2 π x
e ( x x )
2
2 ( 2 x )
1 2 π y
e
2 ( y y )2 ( 2 y )
f X ( x ) fY ( y ) . 所以,随机变量 X 与 Y相互独立.
x x
概率第十六讲 4.3-4.5

北京信息科技大学 统计系
首页 返回 退出
X , Y 独立,X ~ N ( 1 , ), Y ~ N ( 2 , ) 2 2 2 2 aX bY ~ N ( a1 b2 , a 1 b 2 )
2 1 2 2
E ( aX bY ) aE ( X ) bE (Y ) a1 b2 D( aX bY ) a D( X ) b D(Y ) a b ? a1 b2 , a 2 12 b ) aX bY ~ N( 2 ? aX bY c ~ N( a1 b2 c , a b 2 2 )
1 fZ ( z ) e 2π 2
z2 24
, z
1 2z e 2 2
z2 8 z2 8
E | Z | | z | f Z ( z )dz 0
北京信息科技大学 统计系
dz
1 ( 4 e 2
)|
0
4 2
x
1 e 2
t2 2
dt
定理表明:若Yn~B(n, p), 则当n很大, Yn近似服从 N(np,np(1-p)).
北京信息科技大学 统计系
首页 返回 退出
简证: 设Yn~B(n,p), 则Yn表示n重伯努利试验中的 “成功” 次数 . 1 如第i次试验成功 若设 X i i=1,2,…,n 0 如第i次试验失败 则 Yn= X1+X2+…+Xn Xi pk
北京信息科技大学 统计系
首页 返回 退出
已知随机变量X , Y 分别服从N (1, 32 ), N (0, 4 2 ),
X Y (2) Cov( X , Z ) Cov( X , ) 3 2
概率论与数理统计 第四节 二维正态分布
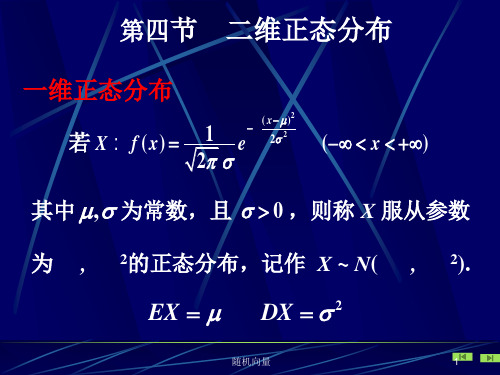
第四节 一维正态分布
二维正态分布
( x )2 2 2
1 e 若 X f ( x) 2
( x )
其中 , 为常数,且 0 ,则称 X 服从参数
( x 1 )2 1 exp 2 2 1 2 1
2 即 X N ( 1 , 1 ).
泊松积分
e
x2
dx
同理可求得关于Y的边缘密度函数为
fY ( y )
f ( x, y )dx
( y 2 ) 2 1 exp 2 2 2 2 2
1 2 2 1 1
x 1 2 x 1 2 2 x 1 2 2 1 exp (1 )( ) ( ) 2 ( ) t t dt 2 1 1 1 2(1 )
( x 1 )2 x 1 2 1 1 exp ( t ) dt exp 2 2 1 2 1 2 1 1 2 2(1 )
2 2
可得 X N ( 1 , 12 ) , Y N ( 2 , 2 2 ) .
证
f X ( x)
1
f ( x , y )dy
2 1 2 1 2
x 1 y 2 y 2 2 x 1 2 1 exp ( ) 2 ( )( )( ) dy 2 1 2 2 2(1 ) 1
概率论与数理统计正态分布4-3二维正态分布课件

二维正态分布的应用场景
金融领域
在金融领域中,二维正态分布常 用于描述股票价格或其他金融变 量的联合分布,帮助投资者进行 风险评估和投资组合优化。
自然学科
在物理、化学、生物等自然学科 中,二维正态分布可用于描述实 验数据的误差分布、气象数据的 联合概率分布等。
概率论与数理统计正态分 布4-3二维正态分布课件源自目录CONTENTS
• 二维正态分布概述 • 4-3二维正态分布特性 • 4-3二维正态分布的性质 • 4-3二维正态分布的统计推断 • 4-3二维正态分布的实际应用
01 二维正态分布概述
二维正态分布的定义
二维正态分布是概率论与数理统计中 一种重要的概率分布,描述了两个随 机变量之间相互独立且具有相同的正 态分布关系。
03
4-3二维正态分布描述了两个随机变量之间线性关系 的情况。
4-3二维正态分布的数学表达式
1
4-3二维正态分布的数学表达式为f(x1, x2) = (1 / (2πσ1σ2)) * exp(-((x1-μ1)^2/2σ1^2 + (x2μ2)^2/2σ2^2))。
2
该表达式描述了两个随机变量x1和x2的概率密度 函数,其中μ1, μ2, σ1^2 和σ2^2是常数。
方差齐性检验
通过检验各组数据的方差是否相等,判断数据是 否满足方差分析的前提条件。
方差分析表
列出各组数据的均值、方差、自由度和贡献度等 信息,用于比较不同组之间的差异。
05 4-3二维正态分布的实际 应用
在金融领域的应用
资产定价
二维正态分布可以用于资产定价模型,例如Black-Scholes模型, 以评估衍生品的价值。
4-3二维正态分布

密度函数, 法1求出Z密度函数,直接随机变量期望的定义 求出 密度函数 求期望和方差. 在例1中求得了Z 求期望和方差 在例1中求得了Z的概率密度
因此由随机变量的期望定义 E(X) = ∫−∞ x f (x)dx 可得
1 e , z >0 fZ (z) = 2 0, z ≤0 ≤0
z − 2
I (x)dx
得到
+∞ x − µ r x R(X,Y) = ∫−∞ σx e 2πσx
2
(x−µx )2 − 2 2σx
dx
置换积分变量
R( X,Y) =
x − µx
σx
x
= t 得到
2πσ ∫
r
t2 − +∞ 2 2 −∞
t e dx = r
∫
t2 +∞ − 2 2 −∞ +∞
2 2
2 2
)
1 ⋅ e 2π
x2 +y2 − 2
=∫
+∞ +∞
−∞ −∞
(x +y ) ∫
2
2 2
dxdy
由极坐标变换公式可得
+∞ − 1 2π 5 E( Z ) = ∫ dθ∫ ρ ⋅ e 2 dρ 0 2π 0 2
ρ2
置换积分变量
2
ρ
2
2
= t, ρ = 2t, 可得
2 +∞ t2 − 2
−∞
=
rσy (x −µx )
σx
−∞
σx
rσy (x − µx )
1−r
t2 +∞ − 2 2 −∞
∫
e dt
=
σx
二维正态分布的原理及应用

二维正态分布的原理及应用1. 引言二维正态分布是概率论中的一个重要概念,它可以帮助我们描述和分析两个变量之间的关系。
本文将介绍二维正态分布的原理及其在实际应用中的一些常见场景。
2. 二维正态分布的定义二维正态分布是指在二维空间中,两个随机变量X和Y的联合概率分布服从正态分布。
其密度函数可以表示为:f(x, y) = (1 / (2 * π * σx * σy * √(1 - ρ^2))) * exp(-((x - μx)^2 / (2 * σx^2)) - ((y - μy)^2 / (2 * σy^2)) + (2 * ρ * (x - μx) * (y - μy)/ (σx * σy)))其中,μx和μy是变量X和Y的均值,σx和σy是标准差,ρ是X和Y之间的相关系数。
3. 二维正态分布的性质二维正态分布具有以下性质: - 边缘分布:X和Y的边缘分布都是单变量的正态分布。
- 相关性:相关系数ρ可以指示X和Y之间的线性相关程度,范围在-1到1之间。
当ρ为0时,X和Y相互独立。
- 条件分布:给定X的值,可以计算出Y的条件概率分布,反之亦然。
4. 二维正态分布的应用4.1. 数据建模二维正态分布常被应用于数据建模领域。
例如,当我们希望分析两个变量之间的关系时,可以使用二维正态分布来估计它们的联合概率分布。
通过了解变量之间的关系,我们可以更好地理解数据,并进行预测和决策。
4.2. 金融风险管理在金融领域中,二维正态分布在风险管理中起着重要作用。
通过建立资产收益率的二维正态分布模型,可以对不同的风险因素进行分析和管理,并进行投资组合优化。
4.3. 工程设计工程设计中常常需要考虑多个变量之间的相互作用。
使用二维正态分布可以模拟系统参数的变化,并进行可靠性分析和优化。
例如,在机械设计中,可以使用二维正态分布来估计零件尺寸的变化范围,并评估系统的可靠性。
4.4. 医学研究在医学研究中,二维正态分布可以用来分析两个变量之间的关系,并研究其对健康和疾病的影响。
二维正态分布
所以( X ,Y )的联合密度为
f ( x, y) f X ( x) fY ( y)
1
( x1)2
e 232
1
e
y2 242
3 2
4 2
1 ( x1)2 y2 e . 18 32
24
6
四、相互独立的一维正态变量的线性组合
若 = 0,则有
f (x, y)
1
e
1[ 2
(
x 1
2 1
)2
(
y
2
2 2
)2
]
2 1 2
1
( x1 )2
e
2
2 12
2 2
,
2 1
2 2
4
f (x, y)
1
e
(
x 1
2
2 1
)2
2 1
1
e
(
y2
2
2 2
)2
2 2
前面说明,
若 (X,Y) ~
N
(1
,
2
,
i 1
i 1
即有限个独立正态变量的线性组合仍然服从正态分布.
7
五、二维正态变量分量的线性组合
若
(
X
,Y
)
服从二维正态分布
N
(1
,
2
,
2 1
,
2 2
,
)
,
则 X 与Y 的线性组合 aX bY 服从正态分布(其中 a, b
是不全为零的常数).
8
§4.6 二维正态分布
1
一、二维正态分布定义
二维正态分布
第14讲 二维正态分布 中心极限定理教学目的:了解二维正态分布,理解独立同分布的中心极限定理和棣莫佛—拉普拉斯定理。
教学重点:独立同分布的中心极限定理。
教学难点:应用独立同分布的中心极限定理解决实际问题。
教学学时:2学时 教学过程:第四章 正态分布§4.4 二维正态分布定义 若二维连续随机变量),(Y X 的联合概率密度为])())((2)([)1(21222222121),(y y yx y x x x y y x r x r y x er y x f σμσσμμσμσπσ-+-------=( +∞<<∞-+∞<<∞-y x , )则称),(Y X 服从二维正态分布,记作 ),,,,(~),(222r N Y X x y x σσμμ。
其中y x μμ,,1|| ,0 ,0<>>r y x σσ都是分布的参数。
),(y x f 满足概率密度的两条基本性质:(1)0),(≥y x f 。
(2)⎰⎰+∞∞-+∞∞-=1),(dxdy y x f 。
下面我们来讨论二维正态分布的边缘分布问题。
随机变量X 的边缘概率密度为⎰⎰∞+∞--∞+∞--==dy erdy y x f x f y x u y x X ),(2121),()(σπσ其中])())((2)([)1(21),(22222yy y x y x x x y y x r x r y x u σμσσμμσμ-+-----=2222])([)1(212)(xx yyx x x r y r x σμσμσμ----+-=设t x r y rxx yy=----])([1212σμσμ,则有⎰∞+∞----=dt eex f tx xX xx 22)(22221)(σμπσ222)(21x x x xeσμσπ--=由X 与Y 的对称性可求得Y 的边缘密度为)(y f Y 222)(21y y y yeσμσπ--=由此可见,二维正态分布的两个边缘分布都是正态分布,并且可以知道)(,)(),(),(Y D X D Y E X E y x y x ====σσμμ下面我们可以看到参数r 为随机变量Y X ,的相关系数。
大学概率论二维正态分布
2
1
π x
y
e dx (ax2 2bxc)
于是
e dx (ax2 2bxc)
π
(
e
acb2 a
)
,
a
f Z (z)
1
e . [
z ( x
2(
2 x
y
2 y
)]2 )
2π
2 x
2 y
由此可见,Z 服从正态分布
N (x
y
,
2 x
2 y
).
定理2表明:
独立正态随机变量的和仍是正态随机变量.
解: 已知 x y 0 , x 16 4 , y
cov(X ,Y ) 12 , 于是 X与Y 的相关系数为 r R( X ,Y ) 12 3, 16 25 5
25 5 ,
概率论与数理统计教程(第四版)
目录
上一页 下一页
返回
结束
第四章
正态分布
§4.4 正态随机变量的线性函数的分布
z
0.015
0.010
0.005 0.000
-10
f (x,y) 2
-5
0
x
5
1 xy 1
exp
2
1 21 2
10
5
0 y
-5
10 -10
x
2 x
2
x
xy
y
2
x
x
y
y
2 y
2 y
概率论与数理统计教程(第四版)
目录
上一页 下一页
返回
结束
§4.3 二维正态分布
[定理1] 设二维随机变量 ( X ,Y )服从二维正态分布
随机向量二维正态分布(“正态分布”相关文档)共8张
分别是X和Y的期望值和标准差.
5
二维正态分布独立的充要条件 定理: 服从二元正态分布的随机变量(X , Y),它们独立 二维正态分布独立的充要条件 的充要条件是X与Y的相关系数r=0. 证: 因为独立必不相关, 因此我们证当X与Y不相关即 定义:如果(X,Y)的联合密度函数为 的充要条件是X与Y的相关系数r=0. 的充要条件是X与Y的相关系数r=0. 的充要条件是X与Y的相关系数r=0. 二维正态分布独立的充要条件
§3.3二维正态分布
1
二维正态分布的定义
定义:如果(X,Y)的联合密度函数为
f
(x,
y)
2
1
12 12
e
xp{2(112)
[(x1)22x1 y2 (y2)2]}
1
1 2
2
则称(X,Y)服从二维正态分布,记为
Hale Waihona Puke (X ,Y )~ N (1 , 1 2 , 2 , 2 2 , )
2
证: 因为独立必不相关, 因此我们证当X与Y不相关即 定理: 服从二元正态分布的随机变量(X , Y),它们独立 分别是X和Y的期望值和标准差. 定理: 服从二元正态分布的随机变量(X , Y),它们独立 定义:如果(X,Y)的联合密度函数为 定义:如果(X,Y)的联合密度函数为 的充要条件是X与Y的相关系数r=0. 的充要条件是X与Y的相关系数r=0. 定理: 服从二元正态分布的随机变量(X , Y),它们独立 二维正态分布独立的充要条件 证: 因为独立必不相关, 因此我们证当X与Y不相关即 证: 因为独立必不相关, 因此我们证当X与Y不相关即 证: 因为独立必不相关, 因此我们证当X与Y不相关即 则称(X,Y)服从二维正态分布,记为 的充要条件是X与Y的相关系数r=0. 的充要条件是X与Y的相关系数r=0.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
关于二维正态分布的一个教学注记
众所周知,二维正态分布是概率论中非常重要的一种分布,其性质也是很重要的,但很多教材在讨论两个正态分布的联合分布是不是二维正态分布这个问题时,要么就是说得不是很清楚,要么就是没有给出例子,要么就是给出的例子比较复杂,其实只要注意到二维正态分布定义中的一个基本事实,这个问题就可以说得很清楚。
首先,给出二维正态分布的定义:如果二维随机变量(X,Y)的概率密度函数为:
其中μ1,μ2,σ1,σ2,ρ均为参数,且σ1>0,σ2>0,ρ<1,则称(X,Y)服从参数为μ1,μ2,σ1,σ2,ρ的二维正态分布,记作(X,Y)(μ1,μ2,σ1,σ2,ρ)。
经过讨论,发现如果(X,Y)服从二维正态分布,那么两个分量X,Y都服从一维正态分布,而且参数ρ就是两个分量X,Y的相关系数,它是不能等于1和-1的,也就是说(X,Y)服从二维正态分布的前提是:两个分量X,Y是正态分布,而且它们的相关系数不是1和-1。
如果二维随机变量(X,Y)的两个分量X,Y是同一正态分布,都是X,那么(X,Y)就不服从二维正态分布,因为两个分量的相关系数是1。
这样我们就很容易解释,为什么两个分量是正态分布,但它们的联合分布不一定是正态分布。
另外,一些教材中往往给出二维正态分布的这样一个性质:
性质:若(X,Y)服从参数为μ1,μ2,σ1,σ2,ρ的二维正态分布,那么(aX+bY,cX+dY)服从二维正态分布。
我觉得这个性质是不严谨的,比如a=c=1,b=d=0这时(aX+bY,cX+dY)为(X,X),两个分量的相关系数为1,(X,X)就不服从二维正态分布。
更一般的,如果a b
c d=0,那么(aX+bY,cX+dY)的两个分量aX+bY和cX+dY成比例,其相关系数为1或-1,(aX+bY,cX+dY)就不服从二维正态分布。
应该再加一个前提,就是行列式a b
c d不等于0,就可以利用二维正态分布的定义证明(aX+bY,cX+dY)服从二维正态分布,这样就没有问题了。
