关于布里渊区

合集下载

布里渊区图示

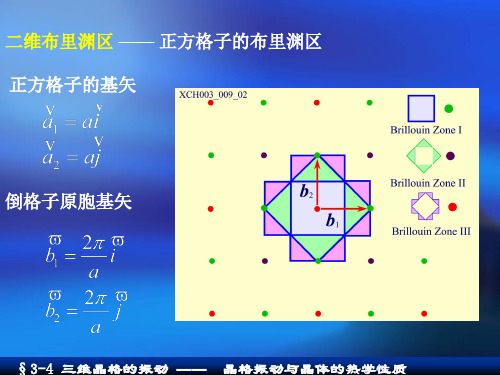
a 3 正格子原胞基矢 a1 ai, a2 i aj 2 2 取单位矢量k垂直于i, j 则，a1，a2和k构成的体积 3 2 a 2
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
倒格子原胞的基矢为 2 (a2 k ) 2 2 b1 i j a 3a 2 (k a1 ) 4 b2 j 3a
的垂直平分线和第一布里渊区边界所围成 —— 第二布里渊区大小
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
第三布里渊区
由4个倒格点
的垂直平分线和第二布里渊区边界边界所围成第三布里渊区大小
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
第一、第二和第三布里渊区
§3-4 三维晶格的振动 ——
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
选一个倒格点为原点，原点的最近邻倒格矢有6个，分别是
b1 , b2 , (b1 b2 )
§3-4 三维晶格的振动 —— 晶格振动与晶体的热学性质
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
晶格振动与晶体的热学性质

正方格子其它布里渊区的形成
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质

正方格子其它布里渊和第一布里渊区重合
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
二维斜格子的第一布里渊区
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质

二维斜格子其它布里渊区的形成
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
二维斜格子其它布里渊区的形状

倒格子与布里渊区

4、面心立方格子的布里渊区
（1）面心立方格子的格子常数（立方边长）为a，倒格子为体心立方，倒格子常数（立方边长）为4/a。（2）第一布里渊区为截角八面体（十四面体） (3) 几个点的坐标： 2/a(0，0，0) X： 2/a(1，0，0) L： 2/a(-½，½ ，½ ) K： 2/a(0，¾，¾ )
2、倒格子
布拉维格子的基矢a1、 a2 、a3为正格子基矢，称Rl=l1a1+l2a2+l3a3决定的空间为正格子，=a1· (a2×a3)为正格子原胞体积。 × 2 × × 定义 1 2 3 3 1
b
1
= 2π a a Ω
为倒格子基矢，由Kh=h1b1+h2b2+h3b3决定的空间为倒格子， =b1· (b2×b3)为倒格子原胞体积。正格子空间的长度量纲是m,倒格子空间的长度量纲为m-1。
3、两种格子原胞间的关系
Ω
*
2π =
Ω
3
倒格子原胞体积与正格子原胞体积存在倒数关系。
4、正格子与倒格子互为对方的倒格子根据倒格子基矢的定义，倒格子的倒格子基矢
b
* 1
×b b = 2π
2
3
Ω*
a1
同理，可以证明 b2*=a2, b3*=a3 倒格子的倒格子就是正格子。
5、正格子（h1h2h3)晶面族与倒格矢Kh正交 Kh•CA=(h1b1+h2b2+h3b3) •(a1/h1-a3/h3)=0 Kh•CB=(h1b1+h2b2+h3b3) •(a2/h2-a3/h3)=0
矢量的乘积
标量积或点积 A· B=|A||B|cos(A,B) 矢量积或叉积任何两个矢量Ａ和Ｂ的矢量积是一个矢量，它的大小等于这两个矢量作成的平行四边形的面积，方向与这个平行四边形所在的平面的垂线方向平行。 |AB|=|ABsin(A,B)|

布里渊区图示

a 3 正格子原胞基矢 a1 = ai, a2 = i + aj 2 2 取单位矢量k垂直于i, j 则，a1，a2和k构成的体积 3 2 Ω= a 2
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
倒格子原胞的基矢为 2π (a2 × k ) 2π 2π b1 = i− j = Ω a 3a 2π (k × a1 ) 4π b2 = = j Ω 3a
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
正方格子其它布里渊区的形成
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
正方格子其它布里渊区的形状
—— 每个布里渊区经过适当的平移之后和第一布里渊区重合
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
二维斜格子的第一布里渊区
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
二维斜格子其它布里渊区的形成
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
二维斜格子其它布里渊区的形状
—— 每个布里渊区经过适当的平移之后和第一布里渊区重合
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
平面正三角形，相邻原子间距为求正格矢和倒格矢求正格矢和倒格矢，平面正三角形，相邻原子间距为a,求正格矢和倒格矢，画出第一和第二布里渊区
的垂直平分线和第一布里渊区边界所围成 —— 第二布里渊区大小
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
第三布里渊区由4个倒格点个倒格点
的垂直平分线和第二布里渊区边界边界所围成第三布里渊区大小
§3-4 三维晶格的振动 ——

布里渊区

固体物理固体物理
布里渊区
主讲人：主讲人：许本超答疑人：答疑人：李海龙封福明
固体物理固体物理
内容
• • • • • • • • • 1.倒易空间 2. 布里渊区基本概念 3. 典型格子的第一布里渊区 4.布里渊区的几何性质 5. 衍射条件在布里渊区诠释 6.布里渊区中的K点 7.布里渊区和能带的关系 8.布里渊区和费米面 9.MS计算能带实例图
14
固体物理固体物理
7.2布里渊区和能带的关系
能带论的基本出发点: 能带论的基本出发点固体中的电子可以在整个固体中运动电子在运动过程中要受晶格原子势场的作用由于周期场的微扰，由于周期场的微扰，
E
E6
E(k)函数在布里渊区函数在布里渊区
允许带
E5
边界k=± 边界 ±nπ/a处出现处出现
3.2体心立方晶格的F.B.Z 体心立方晶格的F.B.Z 体心立方晶格的体心立方晶格的倒格子为面心立方晶格
可以看出，可以看出，面心立方倒格子（即体心立方晶格）格子（即体心立方晶格）的F.B.Z为正菱形十二为正菱形十二面体（非正十二面体）面体（非正十二面体）
8
固体物理固体物理
3.3面心立方晶格的F.B.Z 面心立方晶格的面心立方晶格的F.B.Z 面心立方晶格的倒格子为体心立方晶格
如右图所示，如右图所示，黑框为体心立方倒格子，取其体心（黄点）倒格子，取其体心（黄点）作为原点，红点（8个为原点，红点（8个）为此原点最相邻的倒格点，蓝点（6 点最相邻的倒格点，蓝点（个）为此原点次相邻倒格点可以看出，可以看出，体心立方倒格子（即面心立方晶格）格子（即面心立方晶格）的F.B.Z为截角的八面体为截角的八面体十四面体）（十四面体）

30 布里渊区的知识

��
*简谐近似是晶格动力学处理许多物理问题的出发点!
* 对热膨胀和热传导等问题必须考虑高阶项 --- 特别是3次和4次项的作用 → 这称为非谐项或非谐作用 – V非谐 * 具体处理问题时,把非谐项看成是对起主要作用的简谐项的微扰!
简正振动模式：在简谐近似下, 由N个原子构成的晶体的晶格振动, 可变为3N个独立的谐振子的振动. 每个谐振子的振动模式称为简正振动模式简正振动模式对应着所有的原子都以该模式的频率做振动, 它是晶格振动模式中最简单最基本的振动方式. 原子的振动 —格波振动通常是这3N个简正振动模式的线形迭加.
2

a
i
倒格矢的垂直平分面构成第一布里渊区
a
O
一维晶格点阵
b
-π/a
O
倒格子点阵
π/a
二维晶格点阵的布里渊区取正格子基矢为 a1 ai 和a2 a j 可求出倒格子基矢为
2 2 b1 i 和b2 j a a
作原点0至其它倒格点连线的中垂线，它们将二维倒格子平面分割成许多区域
第三章晶格动力学和晶体的热学性质
固体的许多性质都可以基于静态模型来理解（即晶体点阵模型），即认为构成固体的原子在空间做严格的周期性排列，在该框架内，我们讨论了X 光衍射发生的条件，求出了晶体的结合能，以后还将在此框架内，建立能带论，计算金属大量的平衡性质。然而它只是实际原（离）子构形的一种近似，因为原子或离子是不可能严格的固定在其平衡位置上的，而是在固体温度所控制的能量范围内在平衡位置附近做微振动。只有深入地了解了晶格振动的规律，更多的晶体性质才能得到理解。如：固体热容，热膨胀，热传导，融化，声的传播，电导率，压电现象，某些光学和介电性质，位移性相变，超导现象，晶体和辐射波的相互作用等等。

第一布里渊区

波矢空间固体的能带理论中，各种电子态按照它们的波矢分类。

在波矢空间中取某一倒易点阵为原点，作所有倒易点阵矢量的垂直平分面，这些面波矢空间划分为一系列的区域：其中最靠近原点的一组面所围的闭合区称为第一布里渊区；在第一布里渊区之外，由于一组平面所包围的波矢区叫第二布里渊区；依次类推可得第三、四、…等布里渊区。

各布里渊区体积相等，都等于倒易点阵的元胞体积。

周期结构中的一切波在布里渊区界面上产生布拉格反射,对于电子德布罗意波,这一反射可能使电子能量在布里渊区界面上（即倒易点阵矢量的中垂面）产生不连续变化。

根据这一特点,1930年L.-N.布里渊首先提出用倒易点阵矢量的中垂面来划分波矢空间的区域，从此被称为布里渊区。

第一布里渊区第一布里渊区就是倒易点阵的维格纳－赛茨元胞，如果对每一倒易点阵作此元胞，它们会毫无缝隙的填满整个波矢空间。

由于完整晶体中运动的电子、声子、磁振子、……等元激发（见固体中的元激发）的能量和状态都是倒易点阵的周期函数，因此只需要用第一布里渊区中的波矢来描述能带电子、点阵振动和自旋波……的状态，并确定它们的能量（频率）和波矢关系。

限于第一布里渊区的波矢称为简约波矢，而第一布里渊区又叫简约区，在文献中不加定语的布里渊区指的往往就是它。

布喇菲点阵布里渊区的形状取决于晶体所属布喇菲点阵的类型。

简单立方、体心立方和面心立方点阵的简约区分别为立方体，菱十二面体和截角八面体（十四面体）。

它们都是对称的多面体，并具有相应点阵的点群对称性，这一特征使简约区中高对称点的能量求解得以简化（见晶体的对称性）。

2简约布里渊区简约布里渊区（Reduced Brillouin zone）：由于晶体中的格波或者电子波的色散关系在波矢空间是周期为π/a的周期性函数（例如，E(k) = E(k+n/a)，则k和k+n/a表示相同的状态；因此可把波矢限制在第一Brillouin区(－π/a < q < π/a ) 内，而将其他区域通过移动n/a而合并到第一Brilouin区；在考虑能带结构时, 只需要讨论第一Brilouin 区就够了。

布里渊区

见黄昆书图4－13 （p179)
倒易点阵和14种晶体点阵是一一对应的，因此也只有14种类型的倒易点阵和14种不同形状的第一布里渊区。第一布里渊区的形状只与晶体的布拉维点阵的几何性质有关，与晶体的化学成分、晶胞中的原子数目无关。
布里渊区是一个对称性原胞，它保留了相应
的布拉菲点阵的点群对称性。因此第一布里渊区里依然可以划分为几个完全等同的区域。
由于布里渊区界面是某倒格矢
r
ur G
的垂直平分面，如果
用 k 表示从原点出发、端点落在布里渊区界面上的倒易空
间矢量，它必然满足方程：
k G
1
G2
2
该方程称作布里渊区的界面方程
正方点阵布里渊区
第二到第九Brillouin区约化到第一布里渊区
各布里渊区的形状，不管被分成多少部分，对原点都是对称的
布里渊区定义：在倒易点阵中，以某一格点为坐标原点，做所有
倒格矢的垂直平分面，倒易空间被这些平面分成许多包围原
点的多面体区域，这些区域称作布里渊区，其中最靠近原点
的平面所围成的区域称作第一布里渊区，第一布里渊区界面
与次远垂直平分面所围成的区域称作第二布里渊区，依次类
推得到二维正方格子的布里渊区图见下页。
对一种晶体来说，它的所有布里渊区都有同
样大小的体积，利用平移对称性可以找出第一布里渊区和所有较高的布里渊区Hale Waihona Puke 间的全等性。六方点阵布里渊区图
见黄昆书图4－24 （p194)
Kittel （p28) 黄昆书图4－12（p179)
见黄昆书图4－12 （p179)
体心立方的Wigner-Seitz原胞及第一布里渊区
面心立方的Wigner-Seitz原胞及第一布里渊区

布里渊区的名词解释

布里渊区的名词解释布里渊区是指在光学和无线电工程中，光纤或导波管中因材料非线性而产生的相位调制现象。

这个现象是由于不同频率的光波在光纤中传播时，会发生频率的混合与干涉，导致光波的相位发生变化。

在布里渊区内，光纤中的光波与光纤内部的声波相互作用产生布里渊散射。

布里渊散射是指当光纤中的光波与声波相互作用时，部分光能被散射出去。

这种散射现象是由光波与光纤中声波的相互作用引起的。

光纤中的声波可以由光波引导产生。

当光波在光纤中传播时，由于光纤材料的非线性特性，光波的电场强度会随着光纤中的声波的存在而发生变化。

这种变化会导致光波的相位发生调制。

在布里渊区内，声波的频率与光波的频率非常接近，使得声波与光波发生有效的相互作用。

布里渊区的大小取决于光纤的参数以及传输信号的频率。

对于光纤通信系统来说，布里渊区的存在会对信号的传输产生一定的影响。

当信号频率位于布里渊区时，光纤中的声波与光波的相互作用会导致信号的相位失真和功率损耗。

因此，在设计和实施光纤通信系统时，需要考虑布里渊散射对信号传输的影响，并采取相应的措施来减小布里渊区对信号质量的影响。

布里渊区的现象不仅存在于光纤中，还可以在其他一些导波管（如微纳米波导）中观察到。

这些导波管中的布里渊散射现象也会对波导中传输的信号产生影响。

除了在通信领域中的应用，布里渊区的现象还在光纤传感、光子晶体等领域有着广泛的应用。

通过利用布里渊区的特性，可以设计出基于布里渊散射的传感器，用于测量温度、压力等物理量。

此外，在光子晶体中，布里渊散射也起着重要的作用，可以用于控制和调制光子的传输和储存。

总的来说，布里渊区是光纤或导波管中由于材料非线性而产生的相位调制现象。

它在光纤通信、光纤传感和光子晶体等领域都有着重要的应用。

在光纤通信领域，布里渊散射的存在对信号的传输质量产生一定的影响，因此需要在系统设计中考虑并采取相应的措施来减小布里渊区对信号的影响。

§6.2布里渊区

32
二维长方晶格的布里渊区
33
六角密积结构的第一和第二布里渊区
六角密积结构的第一布里渊区是上下底面为正六边形的多面体。图(a)即是第一布里渊区；图(b)是第二布里渊区的外表面。它与其内的第一布里
渊区边界之间的区域是第二布里渊区。
34
倒格矢的长度(基矢)为:
2 3 Kn a
离原点最近的八个倒格点中垂面所围成的八面体的体积大于倒格子原胞得体积，必须考虑次近邻的六个倒格点。
28
4. 次近邻的倒格点
2 2 2 2 ,0 ,0 0， 2 ,0 0， 2 0， a a a
倒格矢的长度为:
4 K n a
次近邻的六个倒格矢的中垂面将截去原正八面体的六个角，形成一个截角八面体(实际是十四面体)
29
八个面是
正六边形,
六个面是
正四边形
30
2 3 Kn a 4 K nຫໍສະໝຸດ aΓΧΚ
L
2 2 2 3 3 2 1 1 1 0 ,0 ,0 1,0 ,0 波矢k , ,0 , , a a a 4 4 a 2 2 2 31
2b1 , 2b2 2b1 , 2b2
垂直平分线和第二布里渊区边界
边界所围成第三布里渊区大小
2 2 ( ) a
8
第一、第二和第三布里渊区
9
5.正方格子其它布里渊区的形状
10
每个布里渊区经过
适当的平移之后和
第一布里渊区重合
11
6.二维正方格子的能带交叠第一布里渊区在k方向上能量最高点A，k'方向上能量最高点C。 C点的能量比第二布里渊区B点高。

布里渊区

a
jk
,
b2

2
a
k＋i
,
b3

2
a
i j

K n n1b1 n2b2 n3b3
2 a
n2 n3 i n1 n3 j n1 n2 k
20
4
a

b1
b2
b3
21
3.离原点最近的倒格点体心立方的倒格子是面心立方，离原点最近的倒格点有十二个。在直角坐标系中的坐标分别为:
11
6.二维正方格子的能带交叠第一布里渊区在k方向上能量最高点A，k'方向上能量最高点C。 C点的能量比第二布里渊区B点高。
12
二维(包括三维)和一维情形有一个重要的区别—不同能带在能量上不一定分隔开而可以发生能带之间的交叠。第一布里渊区和第二布里渊区能带的重叠。
13
7.二维斜格子的第一布里渊区
第一布里渊区—倒格子空间中的WS原胞。
1
2.布里渊区的特点 (1)各布里渊区的体积相等，都等于倒格子原胞的体积。

＝b1 b2 b3
2 3

(2)波矢k的代表点是均匀分布的，每个代表点的体积为：
1 N1
b1

2 N2
b2

3 N3
b3

14
8.二维六角格子其它布里渊区的形成
15
9.二维六角格子其它布里渊区的形状每个布里渊区经过适当的平移之后和第一布里渊区重合
16
10.二维格子布里渊区的特点 (1)尽管布里渊区在图中看起来好像被分割为不相连的若干小区, 但是,实际上能量是连续的。属于一个布里渊区的能级构成一个能带。不同的布里渊区对应不同的能带。 (2)每个布里渊区的形状尽管各异，但是面积都相等, 等于倒格子原胞的面积。 (3)计入自旋，每个能带包含2N个量子态。 (4)每个布里渊区经过适当的平移之后和第一布里渊区重合。

布里渊区文档

布里渊区什么是布里渊区？布里渊区（BZ）是固体物理学中一个重要的概念，其最早由法国物理学家列昂·布里渊（León Brillouin）在20世纪20年代提出。

布里渊区是借助倒晶格空间来描述晶体中电子和光子的行为的一种方法。

在晶体中，原子排列周期性地重复组成晶格结构。

而倒晶格则是指晶体中的电子和光子在晶格结构的倒数上的重复。

布里渊区即为倒晶格的第一布里渊区，或称为第一布里渊区（First Brillouin Zone，简写为BZ）。

布里渊区的特性布里渊区具有一些重要的特性：1.紧密堆积：布里渊区是以最紧密堆积的原则生成的。

最紧密堆积是指在给定的晶体结构中，原子之间的距离最接近，空隙最小。

2.对称性：布里渊区具有一定的对称性。

这是因为晶体结构在倒晶格上也应当具有一定的周期性。

3.边界：布里渊区是由一系列平面所围成的多面体。

这些边界平面的位置和形状决定了布里渊区的形状。

4.特征矢量：布里渊区内存在一系列称为特征矢量（eigenwave vectors）的矢量。

特征矢量描述了晶格中的固有振动和电子的运动行为。

布里渊区与能带结构布里渊区在研究晶体的能带结构时扮演着重要的角色。

能带结构是指在固体中，能量与波矢之间的关系。

布里渊区的形状和大小直接影响着能带结构和材料的物理特性。

晶体中的电子在能带间跃迁时，受到能量和动量守恒定律的限制。

这意味着电子只能在布里渊区内跃迁。

因此，布里渊区可以看作是晶体中允许电子跃迁的特定动量范围。

通过绘制能带图，我们可以清楚地看到布里渊区内的能带结构。

能带图可以帮助我们理解晶体的电子行为和导电性质。

应用领域布里渊区的概念在固体物理学和材料科学的研究中有着广泛的应用。

一些典型的应用领域包括：1.半导体器件设计：在半导体器件的设计和优化中，布里渊区的概念可以帮助工程师理解晶体中电子的行为，从而指导材料的选择和器件性能的调整。

2.光学材料：布里渊区的理论框架为研究光学材料的光学性质提供了基础。

布里渊区的几何定义

布里渊区的几何定义稿子一嘿，亲爱的小伙伴们！今天咱们来聊聊那个有点神秘但其实也挺有趣的“布里渊区”的几何定义。

你知道吗？布里渊区就像是晶体结构里的一个独特小天地。

想象一下，晶体中的原子们排排站，它们形成的晶格就像一个大迷宫。

而布里渊区呢，就是这个迷宫里划分出来的特别区域。

比如说，它可以看作是在倒格子空间里的一些区域。

倒格子听起来是不是有点晕？别担心，其实就是一种数学上的表示啦。

简单来讲，布里渊区就像是给晶格中的各种波动，比如电子的运动，划分了不同的“领地”。

在每个领地内，这些波动都有自己独特的性质。

比如说，在这个区域里，电子的能量可能会有特定的范围和变化规律。

这就好像每个布里渊区都是电子的一个“专属俱乐部”，只有符合条件的才能进去玩耍。

而且哦，布里渊区的形状和大小，是由晶体的结构决定的。

不同的晶体结构，就有不同形状和大小的布里渊区。

怎么样，是不是觉得布里渊区也没那么难理解啦？稿子二嗨呀，朋友们！今天咱们来探索一下布里渊区的几何定义，准备好了吗？咱们先想象一下，晶体是一个超级大的城市，原子们就是城市里的居民。

而布里渊区呢，就像是城市里划分出来的不同街区。

那它到底是怎么划分出来的呢？这就得提到倒格子啦。

倒格子就像是给这个城市画了一幅特别的地图。

在这张地图上，布里渊区就是那些有特殊意义的区域。

比如说，它们能告诉我们晶体中电子的运动情况。

每个布里渊区都有自己的边界，就像街区有自己的围墙一样。

这些边界可不是随便定的，是根据晶体的对称性和周期性来的。

而且哦，布里渊区的大小和形状能反映出晶体的很多特性。

如果布里渊区比较大，可能说明晶体中电子的活动范围比较广；要是形状比较特别，那也暗示着晶体有独特的性质。

再想想，当我们研究晶体的各种物理性质时，布里渊区就像是一把神奇的钥匙，能帮我们打开很多秘密的大门。

是不是觉得布里渊区挺有意思的？其实只要多想想，这些看似复杂的概念也能变得很简单有趣哟！。

布里渊区

的Wigner-Seitz原胞给出。

金刚石结构的Si、Ge和闪锌矿结构的Ⅲ-Ⅴ族半导体等, 都具有面心立方Bravais格子, 因此都具有体心立方的倒格子, 从而也都具有相同形状的第一Brilouin区, 为截角八面体(即是由6个正方形和8个正六边形构成的14面体)。

3布里渊区的特殊k点采样问题研究介绍在各种周期性边界条件的第一原理计算方法中，需要涉及到在布里渊区的积分问题，例如总能、电荷密度分布，以及金属体系中费米面的确定等等。

如果采用普通的在布里渊区内均匀选取k点的方法，那么为了得到精确的结果点的密度必须很大，从而导致非常大的计算量。

这使得计算的效率非常低下。

因此，需要寻找一种高效的积分方法，可以通过较少的点运算取得较高的精度。

而这些k点被称之为“平均值点”（Baldereschi）或者“特殊点”（Chadi, Cohen）。

[1]基本思想Chadi和Cohen最早提出了这种特殊点的数学基础[1]。

考虑一个光滑函数，我们可以将其展为傅立叶级数：假设另有一个拥有体系全部对称性（对称性用对称群表示）的函数，满足条件，则我们可以将用展开如下：其中是对称群的阶数。

设，将上式的求和顺序重新组合可以得到其中是距离原点第近邻的球半径，按升序排列，且。

需要注意的是限制条件具有球对称性，也即高于的对称性，所以满足限制条件的格点集合并不一定都是等价的——或说可以通过中的操作联系起来的——格点。

方程(3)中的函数满足下列条件：上式中是倒格矢，是满足条件的格点数。

五个方程分别表明函数在第一布里渊区内成奇函数、具有正交性、周期性、体系对称性和完备性。

对于特殊点法而言，前两条更为重要。

注意到上面公式中的求和从1开始，因此需要对的情况进行单独定义。

我们定义，则函数的平均值为：那么该如何得到呢？注意方程(3)，如果存在这样的特殊点，使其满足：>那么立刻可以得到，这样的点被称为“平均值点”。

但是普遍的讲，满足上述条件的点并不存在。

第一布里渊区[110]方向的能带曲线

第一布里渊区[110]方向的能带曲线第一布里渊区[110]方向的能带曲线第一部分：引言能带结构是描述晶体中电子能量分布的重要概念，它对于理解材料的电子性质以及其在各种应用中的表现具有关键意义。

在晶体学中，布里渊区是描述固体中电子能量分布的重要参考区域之一。

本文将着重探讨第一布里渊区[110]方向的能带曲线，对于这一方向上的能带结构有着重要的研究价值。

第二部分：布里渊区的定义布里渊区是由法国物理学家布里渊于1912年提出的，用于描述周期性结构中的电子能量分布。

根据布里渊区的定义，晶体中的电子能量分布能够通过在第一布里渊区内进行分析得到。

第一布里渊区是一个多边形，其边界由实空间中原胞的倒格矢连接而成。

第三部分：[110]方向的能带曲线[110]方向是布里渊区中的一个特定方向，它在晶体学的研究中具有重要的地位。

在研究[110]方向的能带曲线时，我们可以通过布里渊区边界上的特殊点来得到能带的形状和分布。

其中，弥散关系的最大斜率点和最小斜率点是[110]方向上能带曲线的重要特征。

第四部分：能带曲线的形状和分布根据研究结果，[110]方向上的能带曲线通常呈现出抛物线状的形状。

在布里渊区边界上的最大斜率点，能带曲线具有最大弯曲度，电子在此点的速度较大。

而在最小斜率点，能带曲线相对平缓，电子在此点的速度较小。

这些特征对于理解材料的导电性和能带间隙等电子性质具有重要意义。

第五部分：应用前景第一布里渊区[110]方向的能带曲线研究在材料科学和电子器件领域具有广泛的应用前景。

通过对能带曲线的分析，可以研究材料的导电性能、能带间隙以及电子传输等关键参数。

这对于材料的设计和优化具有重要意义，例如在半导体器件中的应用中可以提高器件性能，实现更高的效率和更低的功耗。

第六部分：总结本文主要讨论了第一布里渊区[110]方向的能带曲线，该方向在研究材料的电子性质中具有重要的作用。

我们通过布里渊区边界上的特殊点，描述了能带曲线的形状和分布。

布里渊区

解: a1 ai
a2 bj
2π (i j)
ai b j 2π ij
0 (i j)
b1 2π i a
b2 2π j
b
b
倒格仍为矩形。
a2 bj
a1 ai
a
2π
b
2π
a
j
i
第一区
第二区
例4：画出面心立方第一布里渊区。设面心立方晶格常量为a。
解：面心立方正格基矢：
a1
a
2
布里渊区的形状由晶体结构的布拉菲晶格决定；布里渊区的体积(或面积)等于倒格原胞的体积(或面积)。
aa
a1 ai a2 a j
a2 a j
aa
a1 ai
2π ( i j )
ai b j 2π ij
0 (i j)
b1 2π i a 2π
b2 j a
j
2π
a
2π
a
第一布里渊区
i
第二布里渊区
第三布里渊区
布里渊区的面积
j
=倒格原胞的面积
i
第一区第二区第三区布里渊区的简约区图
a
3
a 2
a 2
a 2
jk ik i j
Ω a1 (a2 a3 )
1 a3 4
ak
a1
aj
倒格基矢:
b1
b2
b3
2π
Ω 2π
Ω 2π
Ω
a2 a3 a3 a1 a1 a2
2π i j k a
2π i j k a
2π i j k a
a2 a3
ai
倒格基矢：
b1
b
b
2π a

I布里渊区简正模和格波

但他们的研究当时被忽视了，因为同年发表的更为简单的Debye热容
理论（弹性波近似）已经可以很好的说明当时的实验结果了，但后来
更为精确的测量却表明了Debye模型不足，所以1935年Blakman才重新
利用Born和Von-Karman近似讨论晶格振动，发展成现在的晶格动力学
理论。后来黄昆先生在晶格振动研究上成就突出，特别是 1954 年和
了“黄方程”，提出了声子极化激元的概念，并与李爱扶（A.Rhys，妻子）建立了多声子跃迁理论。
1947-1952年，与玻恩教授合著《晶格动力学》一书（英国牛津出版社， 1954年）。（2006年中文版）
黄昆对晶格动力学和声子物理学的发展做出了卓越的贡献。他的名字与多声子跃迁理论、X光漫散射理论、晶格振动长波唯象方程、二维体系光学声子模联系在一起。他是“极化激元”概念的最早阐述者。
b1
2
a
i和b2

2
a
j
作原点0至其它倒格点连线的中垂线，它们将二维倒格子平面分割成许多区域
二维正方格子的第一、二、三布里渊区
③ ①②
O
简单立方（sc）
第一布里渊区边界是下面六个倒格矢的中点，并与之正交的平面：
±12��=±
��
��റ��;
Born共同写作的《晶格动力学》一书已成为该领域公认的权威著作。
我国科学家黄昆院士在晶格振动理论上做出了重要贡献。
黄昆院士简介: （摘录） 1945-1947年，在英国布列斯托（Bristol）大学物理系学习，获哲学博士
学位；发表《稀固溶体的X光漫散射》论文，理论上预言“黄散射”。 1948-1951年，任英国利物浦大学理论物理系博士后研究员，这期间建立

常用结构的布里渊区

常用结构和布里渊区(参考书： C.J. Bradley, A.P. Cracknell, “The Mathematical Theory of Symmetry in Solids: Representation Theory for Point Groups and Space Groups”, Oxford, Clarendon Press, 1972)1. 简单立方: Cubic Primitive, c Γ , m3m (O h )正格子：（a,0,0），（0,a,0），（0,0,a ），正格体积 a 3倒格子： )0,0,1(2a π，)0,1,0(2a π，)1,0,0(2a π，倒格体积 338aπ 布里渊区： Fig. 3.13Γ=(0, 0, 0), X=(0, 1/2, 0), M=(1/2, 1/2, 0), R=(1/2, 1/2, 1/2) [注：以上各高对称点单位为： ),,(321b b b , 图上的i i b g=]2. 面心立方: Cubic Face-centred, c f Γ , m3m (O h )正格子：（0,a/2,a/2），（a/2,0,a/2），（a/2,a/2,0），正格体积 a 3/4即： ⎪⎪⎪⎩⎪⎪⎪⎨⎧+=+=+=)(2)(2)(2321j i a a i k a a k j a a（下同）倒格子： )1,1,1(2-a π，)1,1,1(2-a π，)1,1,1(2-a π，倒格体积 3332aπ 即： ⎪⎪⎪⎩⎪⎪⎪⎨⎧-+=+-=++-=)(2)(2)(2321k j i a b k j i a b k j i a bπππ （下同）布里渊区：Fig. 3.14Γ=(0, 0, 0), X=(1/2, 0, 1/2), L=(1/2, 1/2, 1/2), W=(1/2, 1/4, 3/4),K=U=(3/8, 3/8, 3/4)3. 体心立方: Cubic Body-centred, c v Γ , m3m (O h )正格子：)1,1,1(2-a ，)1,1,1(2-a , )1,1,1(2-a , 正格体积 a 3/2 倒格子： )1,1,0(2a π，)1,0,1(2a π，)0,1,1(2a π，倒格体积 3316a π 布里渊区：Fig. 3.15Γ=(0,0,0), H=(1/2,－1/2, 1/2), P=(1/4, 1/4, 1/4), N=(0, 0, 1/2)4. 简单六角: Hexagonal primitive, h Γ , 6/mmm (D 6h )正格子： )0,,0(a -，)0,21,23(a a ，),0,0(c ，正格体积 c a 223 即： ⎪⎪⎩⎪⎪⎨⎧=+=-=k c a j a i a a j a a3212123 原胞图：？重要！：倒格子： )0,1,31(2-a π，)0,0,32(2a π，)1,0,0(2c π，倒格体积 ca 23316π 布里渊区： Fig.3.12Γ=(0, 0, 0), M=(0, 1/2, 0), A=(0, 0, 1/2), L=(0, 1/2, 1/2),K=(－1/3, 2/3, 0), H=(－1/3, 2/3, 1/2)5. 简单四角: Tetragonal primitive, q Γ, 4/mmm (D 4h )正格子： (a, 0, 0)，（0, a, 0），（0, 0, c ），正格体积 a 2c倒格子： )0,0,1(2a π，)0,1,0(2a π，)1,0,0(2c π，倒格体积 ca 238π 布里渊区： Fig. 3.9Γ=(0, 0, 0), M=(1/2, 1/2, 0), Z=(0, 0, 1/2), A=(1/2, 1/2, 1/2),R=(0, 1/2, 1/2), X=(0, 1/2, 0)6. 简单正交: Orthorhombic primitive, o Γ, mmm (D 2h )正格子： (0,-b, 0)，（a,0, 0），（0, 0, c ），正格体积 abc倒格子： )0,1,0(2-b π，)0,0,1(2a π，)1,0,0(2c π，倒格体积 abc38π 布里渊区： Fig. 3.5Γ =(0, 0, 0), Y=(－1/2, 0, 0), X=(0, 1/2, 0), Z=(0, 0, 1/2),U=(0, 1/2, 1/2), T=(－1/2, 0, 1/2), S=(－1/2, 1/2, 0), R=(－1/2, 1/2, 1/2)通常大家遇到的就是以上这些。

布里渊区的物理意义

布里渊区的物理意义布里渊区是指固体中电离位置的相干区域，也可以理解为晶格振动的相干区域。

在布里渊区内，晶格的周期性结构以及原子之间的相互作用会影响电子的行为，因此布里渊区具有重要的物理意义。

首先，布里渊区是描述固体中的电子行为的重要概念。

在固体中，电子会受到晶格周期性结构的影响，同时也与周围电子的相互作用密切相关。

布里渊区的划分可以帮助我们更好地理解电子在固体中的能带结构。

能带结构反映了固体中电子能量与动量之间的关系，而布里渊区的大小和形状决定了能带结构的性质。

通过布里渊区的划分，我们可以更好地理解能带结构对电子输运和电子性质的影响，从而对材料的电学、磁学和光学性质进行更加深入的研究。

其次，布里渊区在研究声子行为和热传导中也具有重要的物理意义。

声子是晶格振动的量子化激发，其行为由晶格的周期性结构决定。

布里渊区的大小和形状决定了声子态的分布和声子能谱的性质。

通过对布里渊区的分析，我们可以了解声子在固体中的散射和衰减行为，从而研究固体材料的热传导性能和热学性质。

此外，对于表面、界面和纳米材料等尺度效应的研究中，布里渊区也扮演了重要的角色。

此外，布里渊区还与光学性质的研究密切相关。

在固体中，电子与光的相互作用是通过吸收、发射或散射光子来实现的。

布里渊区限制了固体中电子和光子之间能量和动量传递的可能性。

通过对布里渊区的研究，可以确定固体材料的光学禁带、折射率、反射率、吸收率和光学色散等性质，进而设计和优化光学器件和材料。

总之，布里渊区具有重要的物理意义，对于描述固体中的电子行为、声子行为和光学性质都发挥着重要的作用。

通过对布里渊区的研究，我们可以更好地理解和预测材料的性能，为材料科学和工程提供指导，并为新材料的设计和合成提供理论基础。

布里渊区

１.二维正方格子的布里渊区

正格子原胞基矢 a ai , a aj 1 2
2 2 b1 a i , b2 a j
• 倒格子原胞基矢：

• 倒格子空间离原点最近的倒格点有四个，相应的倒格子矢为 b1 , b1 , b2 , b2 ，它们的垂直平分线的方程式是
倒格子原胞的体积，也即布里渊区的体积为

a a • 这些垂直平分线围成的区域就是简约布里渊区，也称第一布里渊区。
kx

及k y

• 继续找次近邻倒格点，倒格子矢为
b1 b2 ,(b1 b2 ), b1 b2 ,(b1 b2 )
相应倒格矢的垂直平分线围成区域，构成第二布里渊区。 • 离原点再远一点的倒格点也是4个，倒格子矢为
2b1 ,2b1 ,2b2 ,2b2
相应倒格矢的垂直平分线围成区域，构成第三布里渊区。用同样的方法作出更高一级的布里渊区。
5.5.2 简立方格子
正格子基矢为倒格子基矢为离原点最近的有6个倒格点，它们是它们的中垂面因成的区域，便是第一布里渊区．容易想象得是—个立方体，其体积
次近邻的倒格点有12个
布里渊区
• 布渊区定义：
在倒格子中，以某一倒格点为坐标原点，作所有倒格矢的垂直平分面，倒格子空间被这些平面分成许多包围原点的多面体区域，这些区域称为布里渊区。其中最靠近原点的平面所围的区域称第一布里渊区。第一布里渊区界面与次远垂直平分面所围成的区域为第二布里渊区。第一、第二布里渊区界面与再次远垂直平分面围成的区域为第三布里渊区，依此类推。
由这12个倒格矢的中垂面围成一个菱形12面体，容易验证，该菱形12面体的体积为从菱形12面体中减去第一布里渊区，便是第二布里渊区，它是由6个分离的四棱锥构成，显然它们的体积和等于第一布里渊区体积．

布里渊区

b1(h1 1, h2 1), b2(h1 1, h2 1)
通过这四个倒个是的中点，即
1 2
b1
1 2
b2
a
i
a
j
分别作四个垂直平分面，即可得到第二布里渊区的边界。
照此可以画出第二布区、第三布区等。如右图所示。可以看出，布区的序号越大，分离的区域越多；但不论分离的区域数
目是多少，各布区的面积是相等的。
下面举例说明一维、二维、三维晶格点阵的布里渊区。
（1）一维晶格的布里渊区
一维晶格点阵的基矢为 a ai
对应的倒格子基矢为 b 2 i
a
离原点最近的倒格矢为 b
这些矢量的垂直平分面构成第一布里渊区，其边界为
a
和 b
如图2.5所示。
(2)二维正方格子的布里渊区
设方格子的原胞基矢为 a1 ai a2 aj
1 ( 2 )3
2a
可见，这个截角以后的八面体是第一布里渊区，如图2.8所示。
图2.8 面心立方正格子的第一布里渊区
第一布里渊区种典型对称点的坐标为：
: 2 (0, 0, 0)
a
X : 2 (1, 0, 0)
a
K : 2 (3 , 3 , 0)
a 44
L : 2 (1 , 1 , 1)
a 222
倒格子的原胞基矢为
b1
2
a
i
b2
2
a
j
离原点最近的的倒格点有四个:
b1 , -b1 , b2 , - b2 它们的垂直平分线围成的区域就是简约布里渊区,即第一布里渊区.显然,第一布里渊区是一个正方形,面积为 S*=(2π)2/a2 .
二维方格子布里渊区