1.1 锐角三角函数 公开课获奖课件
合集下载
《锐角三角函数》PPT课件 (公开课获奖)2022年浙教版 (19)
正切 tanα
3 3
1
3
这张表还可以看出许多 知识之间的内在联系?
老师期望: 你能对伴随九个学年的这副三角尺所具有的功能来个 重新认识和评价.
300 454050
450 600
例1 计算: (1)sin300+cos450; (2) sin2600+cos2600-tan450.
老师提示:
Sin2600表示 (sin600)2,
求证:sin2A+cos2A=1
A
老师期望:
B
c
a
┌
b
C
sin2A+cos2A=1它反映了同角之间的三角函数 的关系,且它更具有灵活变换的特点,若能予以 掌握,则将有益于智力开发.
做一做
已知∠A为锐角，且cosA= 你能求出∠A的度数吗。
3，
2
讨论
看图说话: 直角三角形三边的关系. 直角三角形两锐角的关系. 直角三角形边与角之间的关系. 特殊角300,450,600角的三角函数
cos2600表示 (cos600)2,其 余类推.
计算: (1)sin600-cos450;(2)cos600+tan600;
3 2si4n05si6n002co4s05 .
2
4 2si23 n00 co 26s00 2co 24s0.5
2
例2 如图:一个小孩荡秋千,秋千链子的 长度为2.5m,当秋千向两边摆动时,摆角 恰好为600,且两边摆动的角度相同,求它 摆至最高位置时与其摆至最低位置时的 高度之差(结果精确到0.01m).
在毕业聚会中，每两人都握了一次手, 所有人共握手3660次,有多少人参加聚会?
一路下来，我们结识了很多新知识， 也有了很多的新想法。你能谈谈自己的收 获吗？说一说，让大家一起来分享。
1.1.1锐角三角函数(公开课课件)
• 四级
• 五级
试着求一求的值．
A ＝
课堂小结
在Rt△ABC中，如果锐角A确定，
B
∠A的对边
A
┌
∠A的邻边
C
那么∠A的对边与邻边的比随之
确定，这个比叫做∠A的正切.
记作：tanA
∠A的对边
tan A
∠A的邻边
tanA越大，梯子越陡， ∠A越大.
单击此处编辑母版标题样式
随堂练习
1. 如图，△ABC是等腰三角形，你能根据图中所给数据求
，
∴CE=
tan∠EFC＝ =
．
拓展提升
单击此处编辑母版标题样式
随堂练习
(1
). tan60°＝
，tan30°＝
．发现：2tanA
tan2A
（填“＝”或“≠”）
• 单击此处编辑母版文本样式
• 二级
• 三级 中 ， ∠C ＝ 90° ， AC ＝ 3 ， tan
在 Rt△ABC
二级
• 三级
吗？
B
• 四级
• 五级
解：由图可知，D为AC的中点，
则DC=2.
1.5 3
tan C
= .
2 4
1.5
A
D
4
C
如何变化？
倾斜角越大——梯子越陡
1
2
梯子AB和EF哪个更陡？你是如何判断的？
当铅直高度一样，水平宽度越小，梯子越陡.
当水平宽度一样，铅直高度越大，梯子越陡.
梯子AB和EF哪个更陡？你是如何判断的？
如图，小明想通过测量B1C1及AC1 ，
算出它们的比，来说明梯子AB1的倾斜
• 五级
试着求一求的值．
A ＝
课堂小结
在Rt△ABC中，如果锐角A确定，
B
∠A的对边
A
┌
∠A的邻边
C
那么∠A的对边与邻边的比随之
确定，这个比叫做∠A的正切.
记作：tanA
∠A的对边
tan A
∠A的邻边
tanA越大，梯子越陡， ∠A越大.
单击此处编辑母版标题样式
随堂练习
1. 如图，△ABC是等腰三角形，你能根据图中所给数据求
，
∴CE=
tan∠EFC＝ =
．
拓展提升
单击此处编辑母版标题样式
随堂练习
(1
). tan60°＝
，tan30°＝
．发现：2tanA
tan2A
（填“＝”或“≠”）
• 单击此处编辑母版文本样式
• 二级
• 三级 中 ， ∠C ＝ 90° ， AC ＝ 3 ， tan
在 Rt△ABC
二级
• 三级
吗？
B
• 四级
• 五级
解：由图可知，D为AC的中点，
则DC=2.
1.5 3
tan C
= .
2 4
1.5
A
D
4
C
如何变化？
倾斜角越大——梯子越陡
1
2
梯子AB和EF哪个更陡？你是如何判断的？
当铅直高度一样，水平宽度越小，梯子越陡.
当水平宽度一样，铅直高度越大，梯子越陡.
梯子AB和EF哪个更陡？你是如何判断的？
如图，小明想通过测量B1C1及AC1 ，
算出它们的比，来说明梯子AB1的倾斜
全国优质课一等奖人教版九年级数学下册《锐角三角函数》公开课课件
∠所邻的边
斜边
B
=
斜边
c
A
正弦和余弦的注意事项：
b
邻边
a 对边
C
1.sinA、cosA是在直角三角形中定义的，∠A是锐角(注意数形结合，构造直角三角形)。
2.sinA、cosA是一个比值（数值，无单位）。
3.sinA、cosA的大小只与∠A的大小有关，而与直角三角形的边长无关。
课堂练习 （求余弦）
则 = − = − = .
=
= ，
a
b
C
课堂练习 （求余弦）
变式2-3 如图，已知Rt△ABC中，斜边BC上的高AD=4，cosB=，则AC=____.
坡面的绿地进行喷灌。现测得斜坡的仰角为30°，
【问题一】为使出水口的高度为35m，需要准备多长的水管？
∵在直角三角形中，30°角所对的边等于斜边的一边
பைடு நூலகம்
∴ =
1
2
而BC=35 m ∴AB=2BC=70 m
【问题二】如果出水口的高度为50 m，那么需要准备多长的水管？
【问题三】你发现了什么？
100 m
【解题技巧】
1）在 Rt△ABC 中，∠C = 90°，sinA = k，sinB = h，
AB = c，则BC = ck，AC = ch
2）在 Rt△ABC 中，∠C = 90°，sinA = k，sinB = h，
BC=a，则 AB = a ，AC = ah .
k
k
A
b
C
02
锐角三角函数-余弦
在直角三角形中，当锐角 A 的度数一定时，
锐角三角函数比赛课市公开课一等奖省优质课获奖课件.pptx
第4页
比如求sin18°，利用计算器sin键，并输入角 度值18，得到结果sin18°=0.309016994。
又如求tan30°36′，利用tan键，并输入角度、分 值，就能够得到结果0.591398351。 因为30°36′=30.6°，所以也能够利用tan键，并输入
角度值30.6，一样得到结果0.591398351。
（2）cቤተ መጻሕፍቲ ባይዱs a=0.4174;
（3）tan a=0.1890;
（4）cot a=1.3773.
第10页
4、用计算器求下式值.(准确到0.0001) sin81°32′17″+cos38°43′47″
第11页
5.比较大小:
cos30° cos60° tan30° tan60°
第12页
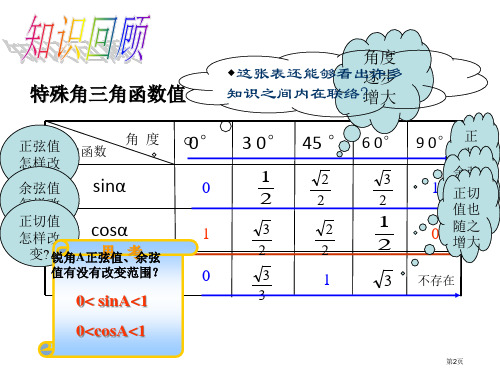
值有没有ta改n变α范围？
0
3
1
3 不存在
0< sinA<1
3
0<cosA<1
第2页
同学们,前面我们学习了特殊角 30°45°60°三角函数值,一些非特殊角 (如17°56°89°等)三角函数值又怎么求 呢?
这一节课我们就学习借助计算器来完成这 个任务.
第3页
这节课我们介 绍怎样利用计 算器求已知锐 角三角函数值 和由三角函数 值求对应锐 角．
特殊角三角函数值
角度 这张表还能够看出逐许步多 知识之间内在联络?增大
正弦值三角函数 角 度 怎样改
余变弦?值 sinα
怎样改
正变切?值 怎样改
cosα
变? 锐角A正弦思值、考余弦
0°
3 0°
45 °
6 0°
9 0°
正 弦
0 1
1 2
比如求sin18°，利用计算器sin键，并输入角 度值18，得到结果sin18°=0.309016994。
又如求tan30°36′，利用tan键，并输入角度、分 值，就能够得到结果0.591398351。 因为30°36′=30.6°，所以也能够利用tan键，并输入
角度值30.6，一样得到结果0.591398351。
（2）cቤተ መጻሕፍቲ ባይዱs a=0.4174;
（3）tan a=0.1890;
（4）cot a=1.3773.
第10页
4、用计算器求下式值.(准确到0.0001) sin81°32′17″+cos38°43′47″
第11页
5.比较大小:
cos30° cos60° tan30° tan60°
第12页
值有没有ta改n变α范围？
0
3
1
3 不存在
0< sinA<1
3
0<cosA<1
第2页
同学们,前面我们学习了特殊角 30°45°60°三角函数值,一些非特殊角 (如17°56°89°等)三角函数值又怎么求 呢?
这一节课我们就学习借助计算器来完成这 个任务.
第3页
这节课我们介 绍怎样利用计 算器求已知锐 角三角函数值 和由三角函数 值求对应锐 角．
特殊角三角函数值
角度 这张表还能够看出逐许步多 知识之间内在联络?增大
正弦值三角函数 角 度 怎样改
余变弦?值 sinα
怎样改
正变切?值 怎样改
cosα
变? 锐角A正弦思值、考余弦
0°
3 0°
45 °
6 0°
9 0°
正 弦
0 1
1 2
九年级数学下册1.1锐角三角函数全国公开课一等奖百校联赛微课赛课特等奖PPT课件
8/13
注意：(1)正弦、余弦概念是在直角三角形中相对其锐 角而定义，其本质是两条线段比，它们只是数值，没有单位， 其大小只与角大小相关，而与其所在三角形边长大小无关.
(2)因为在直角三角形中，边长都是正数，且直角边永
远小于斜边，所以当0°＜∠A＜90°时，0＜sinA＜1,0＜ cosA＜1.
(3)sinA和cosA只表示用一个大写字母表示角正、余弦，
（C）
2. （包头）在Rt△ABC中，∠C=90°，若斜边AB是直角边
BC3倍，则tanB值是
（ ）D
7/13
新知 2 正弦和余弦概念
如图X1-1-5，在△ABC 中，∠C=90°.
1. 锐角A对边与斜边 比叫做∠A正弦，记作 sinA，即sinA=
2. ∠A邻边与斜边比叫做∠A余弦，记作 cosA，即cosA=
对于用三个大写字母表示角，符号“∠”不能省略，如
sin∠A普通写成sinA，而sin∠ABC则不可写成sinABC.
（4）锐角A正弦、余弦和正切都是∠A三角函数，当锐 角A改变时，对应正弦、余弦和正切值也随之改变，改变规
律为∠A越大，则tanA，sinA值越大，cosA值越小.
9/13
【例2】在Rt△ABC中，∠C=90°，AB=13，AC=12，则cosA等
D.
12/13
3. （崇左）如图X1-1-6，在Rt△ABC中，∠C=90°， AB=13，BC=12，则以下三角函数表示正确是 （ ） A
13/13
5/13
【例1】（温州）如图X1-1-4，在△ABC中，∠C=90°， AC=2，BC=1，则tanA值是________.
解析 依据锐角三角函数定义tanA= 可得tanA= BC 1 .
注意：(1)正弦、余弦概念是在直角三角形中相对其锐 角而定义，其本质是两条线段比，它们只是数值，没有单位， 其大小只与角大小相关，而与其所在三角形边长大小无关.
(2)因为在直角三角形中，边长都是正数，且直角边永
远小于斜边，所以当0°＜∠A＜90°时，0＜sinA＜1,0＜ cosA＜1.
(3)sinA和cosA只表示用一个大写字母表示角正、余弦，
（C）
2. （包头）在Rt△ABC中，∠C=90°，若斜边AB是直角边
BC3倍，则tanB值是
（ ）D
7/13
新知 2 正弦和余弦概念
如图X1-1-5，在△ABC 中，∠C=90°.
1. 锐角A对边与斜边 比叫做∠A正弦，记作 sinA，即sinA=
2. ∠A邻边与斜边比叫做∠A余弦，记作 cosA，即cosA=
对于用三个大写字母表示角，符号“∠”不能省略，如
sin∠A普通写成sinA，而sin∠ABC则不可写成sinABC.
（4）锐角A正弦、余弦和正切都是∠A三角函数，当锐 角A改变时，对应正弦、余弦和正切值也随之改变，改变规
律为∠A越大，则tanA，sinA值越大，cosA值越小.
9/13
【例2】在Rt△ABC中，∠C=90°，AB=13，AC=12，则cosA等
D.
12/13
3. （崇左）如图X1-1-6，在Rt△ABC中，∠C=90°， AB=13，BC=12，则以下三角函数表示正确是 （ ） A
13/13
5/13
【例1】（温州）如图X1-1-4，在△ABC中，∠C=90°， AC=2，BC=1，则tanA值是________.
解析 依据锐角三角函数定义tanA= 可得tanA= BC 1 .
浙教版数学九年级下册 1.1 锐角三角函数 课件(共25张PPT)
观察以上计算结果,你发现了什么?
sinA=cosB ，cosA=sinB (∠A+∠B=90）
tanA·tanB=1
(∠A+∠B=90）
B
c
a
┌
A
b
C
sin A a cos A b tan A a
c
c
b
sin B b cos B a
c
c
tan B b a
如图，在△ABC中，若AB=5，BC=3，则下列结论正确
锐角A，A′的余弦值的关系为（ ） A
A．cosA=cosA′ B．cosA=3cosA′ C．3cosA=cosA′ D．不能确定 2．如图，已知P是射线OB上的任意一点，PM⊥OA于M，
且PM：OM=3：4，则cosα的值等于（ C）
3 A．4
4 B．3
C．4 5
3
D．
5
3．在△ABC中，∠C=90°，∠A，∠B，∠C的对边分别是a，
是关于锐角α的三角函数。
AB AB AC
B
A
C
锐角α的正弦，余弦和正切统称∠α的三角函数.
比值 BC 叫做∠α的正弦(sine)，记做sinα.
AB
BC
比值 AC
即sinα= AB
叫做∠α的余弦(cosine) ，记做cosα.
AB
即cosα= AC
AB 比值 叫做∠α的正切(tangent) ，记做tanα.
b，c，则下列各项中正确的是（ ） B
A．a=c·sinB B．a=c·cosB C．a=c·tanB D．以上均不正确
4．在Rt△ABC中，∠C=90°，cosA= 2 ，则tanB等于（ ）
C
锐角三角函数优秀教学课件市公开课一等奖省优质课获奖课件.pptx
用计算器求出以下各角三角函数值，说明你发觉，
并尝试验证.
(1)sin 62°25'30″； (2)sin 80°；
(3)sin 12°25'； (4)cos 27°34'30″;
(5)cos 10°；
(6)cos 77°35'.
【结论】
(1)锐角α正弦值伴随α增大而增大;
(2)sin α=cos(90°-α)，其中α为锐角.
第6页
检测反馈
1.用计算器求sin 62°20'值正确是 ( ) A A.0.8857 B.0.8856 C.0.8852 D.0.8851
解析:按计算器使用说明依次按键得sin 62°20'≈3249，则∠A约为
A.17° B.18° C.19°
(B) D.20°
解析:按计算器使说明依次按键得∠A≈18°.故选B.
3.用计算器求三角函数值(准确到0.001).
(1)sin 23°≈ 0.391 ;
(2)tan 54°53'40″≈ 1.423 .
解析:用计算器求得sin 23°≈0.391，tan 54°53'40″≈1.423.
第7页
4.已知sin α=0.2，cos β=0.8，则α+β≈ 48°24' .(准确到1')
第2页
用计算器求任意锐角三角函数值
求出以下各角三角函数值.
(1)sin 18°； (2)cos 21°28'30″； (3)tan 30°36'.
解:(1)sin 18°≈0.309016994. (2)cos 21°28'30″≈0.930577395. (3)tan 30°36'≈0.591398351.
九年级下《锐角三角函数》ppt省公开课获奖课件说课比赛一等奖课件
(2) BC和 B1C1 , AC 和 AC1, BC
AB AB1 AB AB1 AC
和 B1C1有什么关系?
AC1
BC = B1C1 AB AB1
AC AC1 =
AB AB1
BC B1C1 =
AC AC1
C1
想一想
B
ß
A
C
(1)直角三角形AB1C1和直角三 角 形ABC有什么关相系同?
B1 (2) BC 和 B1C1 , AC 和 AC1, BC
AB AB1 AB AB1 AC
和B1C1 有什么关系?
AC1
BC B1C1
=
AB AB1
AC AC1
=
AB AB1
BC B1C1
=
AC AC1
(3)假如变化B在梯子上旳位置，
（2）中旳关系还存在吗？
即在直角三角形中，锐角 不变时， 旳
对边与斜边旳比、邻边与斜边旳比、对边
C1 与邻边也不变
（4）若变化角度为 ß时，以上比
要点和难点：
1.本节教学旳要点是锐角旳正弦、余弦和正切和锐角三角函数旳概念。 2. 锐角三角函数是将与锐角有关旳比值作定义,可本简介了正弦、余弦
和正切三类,不论从函数旳意义还是锐角三角函数旳符号,以及函数中 以角为自变量,都有别于已学过旳一次函数和二次函数,其概念比较抽 象，是本节教学旳难点。
课后反思
为锐角∠A旳三角函数.
1、sinA 不是一种角 2、sinA不是 sin与A旳乘积 3、 sinA 是一种比值 4、sinA 没有单位
例题1： 求出图所示旳Rt△ABC中,∠C=900,AB=5,
BC=3.求∠A旳三个三角函数值.
图 19.3.1
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
A. 5
B.12
C. 5
D.12
12
5自动扶梯的长l为10 m，该自动扶梯到达的高度h为6 m，自动扶梯与 地面所成的角为θ，则tanθ的值等于( A )
A.3
B.4
C.3
D.4
4
3
5
5
9．(10分)先分别求出图①、②的直角三角形中两个锐角的正弦值、余弦值、正切值．
FC BC
∵D 是 AB 的中点，DG∥BC，∴AG＝DG＝AD＝1，∴AG＝1AC，HG＝DG＝1.∴AC
AC BC AB 2
2 FC BC 2
＝2GC，FC＝2HG，BC＝2DG.又∵AC＝2EF，∴GC＝EF，即 GF＋FC＝EG＋GF，∴EG＝ FC，∴EG＝2HG.又∵DH⊥EG，∴DE＝DG，∴BC＝2DE.
14．(8分)如图，在Rt△ABC中，∠ACB＝90°，D是AB的中点，过点D作AB的垂线交AC于点E，BC＝6，
sinA＝ 3 ，求DE的长 5
解：∵BC＝6，sinA＝3，∴AB＝10，∴AC＝ 102－62＝8.∵D 是 AB 的中点，∴AD＝1AB
5
2
＝5.易证△ADE∽△ACB，∴DE＝AD，即DE＝5，解得 DE＝15.
BC AC 6 8
4
16．(14分)(原创题)如图，在△ABC中，AB＝AC＝8，BC＝4，BF⊥AC于F，D是AB的中点，E是AC上一点， 且AC＝2EF. (1)求证：BC＝2DE； (2)求tan∠DEF的值．
解：(1)证明：分别过点 D 作 DG∥BC 交 AC 于 G，DH⊥AC 于 H，∵DG∥BC，∴∠DGH＝∠ C.又∵∠DHC＝∠BFC＝90°，∴△DHG∽△BFC，HG＝DG.
第1章 解直角三角形
1．1 锐角三角函数
第1课时 锐角三角函数的概念
浙教版·九年级全册
1．(5分)如图，在△ABC中，∠C＝90°，AB＝13，BC＝5，则sinB的值是( C )
A. 5
B. 5
C.12
D.12
13
12
13
5
2．(5分)如图，将∠AOB放置在5×5的正方形网格中，则tan∠AOB的值是( B )
(2)在等腰△ABC 中，BC 上的高为 AB2－（1BC）2＝2 15.∴BF·AC＝2 15·BC， 2
∴BF＝ 15，∴FC＝ BC2－BF2＝1.由(1)知∠DEF＝∠DGH＝∠C，∴tan∠DEF＝tanC＝BF FC
＝ 15.
A.2
B.3
C.2 13
D.3 13
3
2
13
13
3．(5分)把△ABC三边的长度都扩大为原来的3倍，则锐角A的正弦函数值( A )
A．不变
B．缩小为原来的 1
C．扩大为原来的3倍
D．不能确定 3
4．(5分)(教材P6作业题T4变式题)在△ABC中，若三边BC，CA，AB满足BC∶CA∶AB＝5∶12∶13，则 cosB＝( C )
解：图①：sinA＝ 5 ，cosA＝12，tanA＝ 5 ；sinB＝12，cosB＝ 5 ，tanB＝12.
13
13
12
13
13
5
sinF＝3 13，cosF＝2 13，tanF＝3；sinD＝2 13，cosD＝3 13，tanD＝2.
13
13
2
13
13
3
图②
13.(5分)已知，在平面直角坐标系xOy中，已知一次函数y＝kx＋b(k≠0)的图象过点P(1，1)，与x轴 交于点A，与y轴交于点B.若tan∠ABO＝3，那么点A的坐标是___(_－__2_，__0_)_或__(4_，__0_)_____． 点拨：分当一次函数图象与x正半轴相交和与x负半轴相交两种情况进行讨论．