超静定问题解法例说
05-扭转超静定问题及其解法 课件在线观看

♦扭转超静定问题的解法
扭转超静定问题
求解方法 解除多余约束法
♦扭转超静定问题的解法,
例1.两端固定的圆截面等直杆48 ,在截面C处受 扭 转力偶矩皿作用,如图所示。已知杆的扭转刚 度 为G/p。试求杆两端的约束力偶矩以及C截面的 扭 转角。
♦扭转超静定问题的解法
解:受力分析可知,圆杆有二个未知约束力偶、,MB,但只有一个独立的 静力平衡方程:
基本静定系应满足如下的的变形相容条件:
^ 一如 BMe
MB
♦扭转超静定问题的解法
物理方程代入变形相容方程中:
_ Mea =瓦瓦 MBl
补充方程
♦扭转超静定问题的解法
由此求得“多余”未知力,亦即约束力偶MB为:
M B
Mea
=~f~
(-。
另一约束力偶M4可由平衡方程求得为:
♦扭转超静定问题的解法
根据截面法,圆杆刀。段横截面上的扭矩为
E MX = 0, MA - Me + MB = 0
一次超静定
♦扭转超静定问题的解法, 亠
解除圆杆8端约束,代以多余约束力偶的,得到基本静定系
♦扭转超静定问题的解法
基本静定系
1. 静定结构 2. 作用有初始荷载和多余未知约束力 3. 在多余约束处的位移需满足变形相容条件才等价 于原超静定结构
从而有
、 a - Me1aGbT/z
♦扭转超静定问题的解法
扭转超静定问题的一般解法
1. 受力分析,列出静力平衡方程,确定超静定次 数;
2. 解除多余约束,施加多余未知力,得到基本静定 系;
3. 在多余约束处列出变形相容方程,物理方程代 入,得到补充方程;
___ 4. 联立求解得到所有约束反力。
超静定问题解法例说

超静定问题解法例说-1-超静定问题解法例说[浙江永嘉县上塘中学 35100 钱呈祥]物理习题中,未知量的个数与独⽴⽅程的数⽬⼀致时,称为静定问题。
即能够由独⽴⽅程的求解,确定该系统中所有的未知量;若未知量个数⼤于独⽴平衡⽅程数⽬,则称为超静定问题。
对于超静定问题,常需根据题⽬的相关材料,建⽴补充⽅程(辅助⽅程),再与独⽴⽅程联⽴,才能求解,⼀般难度较⼤。
超静定问题,实则为补充⽅程如何建⽴的问题。
例⼀:如图1所⽰,刚性板由三根相同的弹簧悬挂,其重量为G ,重⼼在O 处,试求三根弹簧的受⼒。
[解析]AB 板受⼒如图,由∑=0F ,得F 1+F 2+F 3=G (1)由∑=0M ,得F 1〃223lF aG l=+ (2)据平衡条件只有这两个⽅程,⽽未知量有三个,因此它属于超静定⽅程。
由变形情况的⼏何关系有:△l 1+△l 3=2△l 2 由胡克定律,上式即化为2312F k F k F =+ (3)联合(1)(2)(3),得F 1=G (l a-31),F 2=3G ,F 3=G (l a+31)评论:该超静定问题的求解,除了建⽴原⼒系的平衡⽅程外,关键在于找出变形的⼏何关系,再代⼊胡克定律,以建⽴补充⽅程。
在进⾏变形分析时,变形与受⼒的假设⽅向须保持⼀致。
例⼆:已知地球半径为R ,地球表⾯的重⼒加速度为g ,求:(1)在距地⾯⾼h 的轨道上的⼈造地球卫星的速度;(2)该卫星的周期。
[解析]地球对⼈造卫星的万有引⼒提供卫星做圆周运动的向⼼⼒,可列出独⽴⽅程:)()(22h R V m h R GMm +=+ (1),式中M 和V均为未知量。
可列出补-2- 充⽅程:g R GM mg R GMm ==22,即(2)联合(1)、(2)式可得 V 2=g h R Rh R V h R T h R g R V h R g R h R GM ++=+=+=+?=+)(2)(2,,2ππ从⽽评论:在应⽤万有引⼒定律解题时,常已知星球表⾯引⼒加速度⽽不知星球质量或者已知星球质量⽽不知星球表⾯引⼒加速度,此时均可⽤补充⽅程G g R M =2。
材料力学简单的超静定问题

1.94
37
小 结
1、明确超静定、超静定次数、多余约束、 多余未知力、基本静定系等基本概念。 2、能判断超静定次数。 3、理解超静定问题的基本解法为考虑静 力平衡、变形相容和物理关系三个方面。 4、对于二次或二次以下的超静定问题, 能合理地选取基本静定系,正确地列出 变形几何方程。 5、初步学习利用对称性降低超静定次数、 选取基本静定系的技巧。
超静定次数: 未知力个数与独立平衡方程数之差,也等于多 余约束数。由于超静定结构能有效降低结构的内力 及变形,在工程上(如桥梁等)应用非常广泛。
4
二、求解超静定问题的基本方法
1.静定与超静定的辩证关系 多余约束的两种作用: 增加了未知力个数,同时增加对变形的限制与约束 前者使问题变为不可解;后者使问题变为可解。 2.超静定的处理方法 平衡方程
解除B端多余约束,代之以约束反力 R B
8
§6-2
拉压超静定问题
A
E1 A1
(2)建立变形协调方程。
AB BF BB 0
(3)物理方程。
F 1 BF AC () E1 A1 BB AB RB ( 1 2 )() E1 A1 E2 A2
目录
A
B FBy
C
(d)
3 FAy F ( ) 4
33
§6-4 简单超静定梁
例 8 梁AB 和BC 在B 处铰接,A、C 两端固定,梁的抗弯刚度 均为EI,F = 40kN,q = 20kN/m。画梁的剪力图和弯矩图。 解 从B 处拆开,使超静定结构变 成两个悬臂梁。 变形协调方程为: yB1 yB 2
(3)代入物理关系,建立补充方程
②
2
A
3
超静定问题PPT课件
FN1 cos FN2 cos FN3 F 0
FN1
FN 3
EA cos2
E3 A3
FN3 1 2
F EA
cos2
E3 A3
FN1
FN 2
1 2cos
F
E
E3 A3
A cos2
第13页/共59页
B 1
1
Δl3
D
3
C 2
A
3 F2
A
Δl1A' NhomakorabeaFA A C
F
B FB
14
b
a
l
第六章 简单的超静定问题
例题2 求图a所示等直杆AB上,下端的约束力, 并求C截面的位移。杆的拉压刚度为EA。
解: 1. 列平衡方程 有两个未知约束力FA , FB(见图a),但只有一个独 立的平衡方程
FA+FB-F=0 为一次超静定问题。
第14页/共59页
2. 取固定端B为“多余”约束。相应 的相当系统如图b,它应满足相容条件 ΔBF+ΔBB=0,参见图c,d。
MA 0
F a F 2a 0
A
B
P
FN1 a
A
FN2 a
FN3 B
P
第17页/共59页
变形协调方程:
ΔL 1
L1 L3 2(L2 L3 ) (2)
物理方程:
l1
FN 1l EA
l2
FN 2l EA
l3
FN 3l EA
(3)
联解(1)(2)(3)式得:
F 5P 6
F
2
1 3
P
F
3
1 6
D
由位移相容条
简单的超静定问题 超静定问题及其解法

( wB ) FBy
C C F F
8FBy a 3 3EI
(b) (b)
B B
所以
3 14 Fa 3 8FBy a 0 3EI 3EI
MA
MA MA
A A
B B (c) (c) B B B (d) (d) FBy FBy
FA y
A A A
C C
7 FBy F 4
4)由整体平衡条件求其他约束反力
第六章 简单的超静定问题
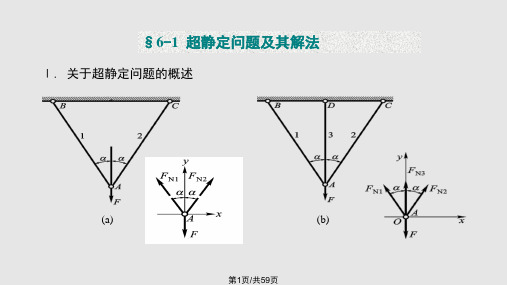
§6-1 超静定问题及其解法
§6-2 拉压超静定问题
§6-3 扭转超静定问题 §6-4 简单超静定梁
§6-1 超静定问题及其解法
超静定问题与超静定结构:未知力个数多于独立 的平衡方程数。 超静定次数:未知力个数与独立平衡方程数之差。 变形几何相容方程:有多余约束的存在,杆件(或 结构)的变形受到多于静定结构的附加限制。根据 变形的几何相容条件,建立附加的方程。
7-6
目录
采用超静定结构
MA MA FA y FA y
A A 2a 2a (a) (a) A A
B B a a
F F
C C
例 求梁的支反力,梁的抗弯 刚度为EI。 解:
1)判定超静定次数
(b) (b)
B B F F FBy FBy B B B
C C
2)解除多余约束,建立相当系统 3)进行变形比较,列出变形协调 条件
FN1 FN 2 33.3kN
FN 2 2 33.3MPa A2
FN 1 1 66.7MPa A1
例:设温度变化为t,1、2杆的膨胀系数为1, 3杆
的膨胀系数为3,由温差引起的变形为l= •t •l,
求各杆温度应力。
材料力学超静定全版
F3 b 3 EA
4. 变形几何协调条件
F1 A
F2
③
2 2 1
3 31
B
C
D F
位移法 1. 假设θ已知 2. 变形几何协调条件
θ
A
①
②
③ D F
1 l
2 2l
3 3l
3. 三杆轴力 EA EA F1 1 l b b
EA EA F2 2 2l b b EA EA F3 3 3l b b
3
A 0
ql 2 MA 8
§2 拉压超静定问题 例1. EA已知,求B处约束力。
A a C B F b
(1)
(2)求B处位移
AC
F FB a
EA EA
BC
FB b EA
A C B FB
B
F FB a FB b
EA
F
(3)变形协调
B 0
B
C
q
A B
C
C FCD
A
B
C
q
FCD C A B FCDl A B C
FCD
A
B
C
ql2/2
A B C q B C A FCDl
ql2/2 A
B
C
q A B C q B C A FCDl B
ql2/2 -FCDl
A
B
C
ql2/2 A
FCD C
q2l 3 ql 2 / 2 FCD l 2l ql 4 FCD l 3 C l 24 EI 3 EI 8 EI 3 EI
C
B1 B 2
§2-8 拉伸、压缩超静定问题.
=cm2 , =cm2,当温度升至T2
=25℃时,求各杆的温度应力。 a (线膨胀系数 =12.5× 106 / C N1 a 弹性模量E=200GPa) 解:、平衡方程: ;
Y N N
1
2
0
、几何方程:
a
L LT LN 0
A A1 100 0 0 A
3、脆性、塑性及相对性
以 5 0 0 为界
四、无明显屈服现象的塑性材料
0.2
名义屈服应力:
0.2
,即此类材料的失效应力。
.
bL
五、铸铁拉伸时的机械性能
bL ---铸铁拉伸强度极限(失效应力)
E t g ; 割线斜率
六、材料压缩时的机械性能
应力越高蠕变越快
蠕变变形是不可恢复的塑性变形。
2、应力松弛:
在一定的高温下,构件上的总变形不变时,弹性变形会随时 间而转变为塑性变形(原因为蠕变),从而使构件内的应力变小 。这种现象称为应力松弛。
加静载
经过较长时间后 卸载
杆也是自己长了一段!
温度不变 3 2 1
初始弹性应变不变
T1T2 T3
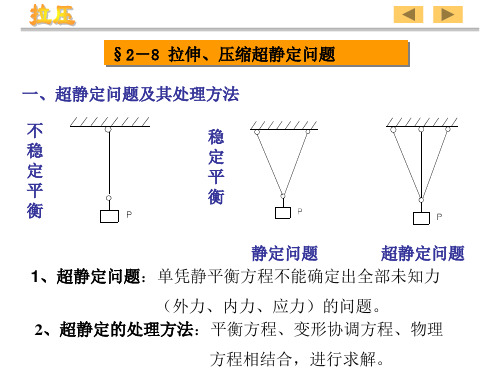
§2-8 拉伸、压缩超静定问题 一、超静定问题及其处理方法 不 稳 定 平 衡 稳 定 平 衡
静定问题 超静定问题 1、超静定问题:单凭静平衡方程不能确定出全部未知力 (外力、内力、应力)的问题。 2、超静定的处理方法:平衡方程、变形协调方程、物理 方程相结合,进行求解。
例11 设1、2、3三杆用铰链连接如图,已知:各杆长为:
N ( x) P() P()
其中“P()”与“P()”均为x点左侧与右侧部分的 所有外力。
简单的超静定问题

M A Me M B 0
Me MB
A
C
B
2、变形协调方程
B 0
即
BM BM 0
e B
Me
MB
A
C
B
3、补充方程
BM
e
M e a GI p
BM
BM Bl GI p NhomakorabeaM e a M Bl 0 GI p GI p
M ea MB l
4、联立解得
3、物理方程
FN 1l l1 EA FN 3 l l 3 EA FN 2 l l 2 EA
得
FN 1 FN 2 FN 3
F 12 F 3
C′
补充方程 FN 1 FN 3 2FN 2
7F 12
例题3:如图所示结构,杆①、②的刚度为EA,梁BD 为刚体,载荷F=50kN,许用应力[s]160MPa。试确 定各杆的横截面积。 解: 1、确定各杆内力 取横梁为研究对象 平衡方程
FB aEAT
由平衡方程得 FA FB aEAT
例题5:如图所示结构,三杆的刚度均为EA,杆③的长 度比设计长度l短了d。试求装配后各杆的轴力。
A
D
① ③ a a C′ C l2 ②
B
解:对称结构,内力对称 变形协调方程
l1 d l 3 cos a
l
d
l3 l1
lt a1 T l1 a 2 T l 2
A
l1
C
l2
B
约束力产生的变形
l FB FB l1 F l B2 E1 A1 E2 A2
lt
FB
变形协调方程
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
-1-
超静定问题解法例说
[浙江永嘉县上塘中学 35100 钱呈祥]
物理习题中,未知量的个数与独立方程的数目一致时,称为静定问题。
即能够由独立方程的求解,确定该系统中所有的未知量;若未知量个数大于独立平衡方程数目,则称为超静定问题。
对于超静定问题,常需根据题目的相关材料,建立补充方程(辅助方程),再与独立方程联立,才能求解,一般难度较大。
超静定问题,实则为补充方程如何建立的问题。
例一:如图1所示,刚性板由三根相同的弹簧悬挂,其重量为G ,重心在O 处,试求三根弹簧的受力。
[解析]AB 板受力如图,由∑=0F ,得F 1+F 2+F 3=G (1)
由∑=0M ,得F 1〃223l
F a
G l
⋅=⋅+ (2)
据平衡条件只有这两个方程,而未知量有三个,因此它属于超静定方程。
由变形情况的几何关系有:△l 1+△l 3=2△l 2 由胡克定律,上式即化为23
1
2F k F k F =+ (3)
联合(1)(2)(3),得
F 1=
G (l a
-31),F 2=3G ,F 3=G (l a
+31)
评论:该超静定问题的求解,除了建立原力系的平衡方程
外,关键在于找出变形的几何关系,再代入胡克定律,以建立
补充方程。
在进行变形分析时,变形与受力的假设方向须保持一致。
例二:已知地球半径为R ,地球表面的重力加速度为g ,求:(1)在距地面高h 的轨道上的人造地球卫星的速度;(2)该卫星的周期。
[解析]地球对人造卫星的万有引力提供卫星做圆周运动的向心力,可列出独立方程:)()(2
2h R V m h R GMm +=+ (1),式中M 和V
均为未知量。
可列出补
-2- 充方程:
g R GM mg R GMm ==22,即 (2)联合(1)、(2)式可得 V 2=g h R R
h R V h R T h R g R V h R g R h R GM ++=+=+=+⋅=+)(2)(2,,2ππ从而 评论:在应用万有引力定律解题时,常已知星球表面引力加速度而不知星球质量或者已知星球质量而不知星球表面引力加速度,此时均可用补充方程G g R M =2。
例三:把一个标有“10V ,2W ”的纯电阻用电器甲,接入一个电动势ε恒定的电源时,甲实际消耗的功率为2W ;把一个“10V ,5W ”的纯电阻用电器乙接入同一电源时,乙实际消耗的功率是否有可能小于2W ?如认为不可能,请说明理由;如认为可能,请找出条件。
设用电器的电阻值不随温度改变。
[解析]用电器甲的电阻R 1=)(502
102
121欧==P U ,用电器乙的电阻R 2=)(205102222欧==P U ,据题意知:P 1=50)50(2,)(2121⋅+=⋅+r
R r R εε即可化为, r 2.010+=ε (1)
,这一个独立方程包含两个未知数,则既解不出电源电动势ε,也解不出电源内阻r ,属于超静定方程。
可以用自洽的方法,假设乙用电器实际消耗功率可能小于2W ,建立一个补充方程:)(2)('2222W R r R P <⋅+=ε
(2)联合方程(1)和不等式(2)可解得r>1010(伏),由此可见,用电器乙实际功率小于2W 是可能的,条件是电源电动势ε>(10+210)伏,内阻r>1010欧,且同时满足ε=10+0.2r 的关系。
评论:该超静定问题是用全电路欧姆定律及补充方程解得的,此外还可以用U-I 图线法讨论。
