计量经济学 简单线性回归 实验报告
EViews计量经济学实验报告-简单线性回归模型分析
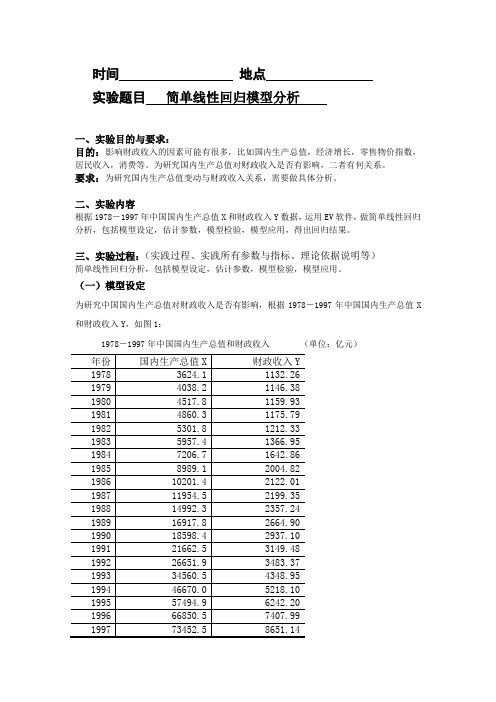
时间地点实验题目简单线性回归模型分析一、实验目的与要求：目的：影响财政收入的因素可能有很多，比如国内生产总值，经济增长，零售物价指数，居民收入，消费等。
为研究国内生产总值对财政收入是否有影响，二者有何关系。
要求：为研究国内生产总值变动与财政收入关系，需要做具体分析。
二、实验内容根据1978－1997年中国国内生产总值X和财政收入Y数据，运用EV软件，做简单线性回归分析，包括模型设定，估计参数，模型检验，模型应用，得出回归结果。
三、实验过程：（实践过程、实践所有参数与指标、理论依据说明等）简单线性回归分析，包括模型设定，估计参数，模型检验，模型应用。
（一）模型设定为研究中国国内生产总值对财政收入是否有影响，根据1978－1997年中国国内生产总值X 和财政收入Y，如图1：1978－1997年中国国内生产总值和财政收入（单位：亿元）根据以上数据，作财政收入Y 和国内生产总值X 的散点图，如图2：从散点图可以看出，财政收入Y 和国内生产总值X 大体呈现为线性关系，所以建立的计量经济模型为以下线性模型：01i i i Y X u ββ=++（二）估计参数1、双击“Eviews ”，进入主页。
输入数据：点击主菜单中的File/Open /EV Workfile —Excel —GDP.xls;2、在EV 主页界面点击“Quick ”菜单，点击“Estimate Equation ”,出现“Equation Specification ”对话框，选择OLS 估计，输入“y c x ”,点击“OK ”。
即出现回归结果图3：图3. 回归结果Dependent Variable: Y Method: Least Squares Date: 10/10/10 Time: 02:02 Sample: 1978 1997 Included observations: 20Variable Coefficient Std. Error t-Statistic Prob. C 857.8375 67.12578 12.77955 0.0000 X0.1000360.00217246.049100.0000R-squared 0.991583 Mean dependent var 3081.158 Adjusted R-squared 0.991115 S.D. dependent var 2212.591 S.E. of regression 208.5553 Akaike info criterion 13.61293 Sum squared resid 782915.7 Schwarz criterion 13.71250 Log likelihood -134.1293 F-statistic 2120.520 Durbin-Watson stat0.864032 Prob(F-statistic)0.000000参数估计结果为：i Y = 857.8375 + 0.100036i X（67.12578） （0.002172）t =（12.77955） （46.04910）2r =0.991583 F=2120.520 S.E.=208.5553 DW=0.8640323、在“Equation ”框中，点击“Resids ”,出现回归结果的图形（图4）:剩余值（Residual ）、实际值（Actual ）、拟合值（Fitted ）.（三）模型检验1、 经济意义检验回归模型为：Y = 857.8375 + 0.100036*X （其中Y 为财政收入，i X 为国内生产总值；）所估计的参数2ˆ =0.100036，说明国内生产总值每增加1亿元，财政收入平均增加0.100036亿元。
《计量经济学》eviews实验报告一元线性回归模型详解
计量经济学》实验报告一元线性回归模型-、实验内容（一）eviews基本操作（二）1、利用EViews软件进行如下操作：（1）EViews软件的启动（2）数据的输入、编辑（3）图形分析与描述统计分析（4）数据文件的存贮、调用2、查找2000-2014年涉及主要数据建立中国消费函数模型中国国民收入与居民消费水平:表1年份X(GDP)Y（社会消费品总量）200099776.339105.72001110270.443055.42002121002.048135.92003136564.652516.32004160714.459501.02005185895.868352.62006217656.679145.22007268019.493571.62008316751.7114830.12009345629.2132678.42010408903.0156998.42011484123.5183918.62012534123.0210307.02013588018.8242842.82014635910.0271896.1数据来源：二、实验目的1.掌握eviews的基本操作。
2.掌握一元线性回归模型的基本理论，一元线性回归模型的建立、估计、检验及预测的方法，以及相应的EViews软件操作方法。
三、实验步骤（简要写明实验步骤）1、数据的输入、编辑2、图形分析与描述统计分析3、数据文件的存贮、调用4、一元线性回归的过程点击view中的Graph-scatter-中的第三个获得在上方输入Isycx回车得到下图DependsntVariable:Y Method:LeastSquares□ate:03；27/16Time:20:18 Sample:20002014 Includedobservations:15VariableCoefficientStd.Errort-StatisticProb.C-3J73.7023i820.535-2.1917610.0472X0416716 0.0107S838.73S44 a.ooao R-squared0.991410 Meandependentwar119790.2 AdjustedR.-squared 0.990750 S.D.dependentrar 7692177 S.E.ofregression 7J98.292 Akaike infocriterion20.77945 Sumsquaredresid 7；12E^-08 Scliwarz 匚「爬伽20.37386 Loglikelihood -1&3.3459Hannan-Quinncriter. 20.77845 F-statistic 1I3&0-435 Durbin-Watsonstat0.477498Prob(F-statistic)a.oooooo在上图中view 处点击view-中的actual ,Fitted ,Residual 中的第一 个得到回归残差打开Resid 中的view-descriptivestatistics 得到残差直方图/icw Proc Qtjject PrintN^me FreezeEstimateForecastStatsResids凹Group:UNIIILtD Worktile:UN III LtLJ::Unti1DependentVariablesMethod;LeastSquares□ate:03?27/16Time:20:27Sample(adjusted):20002014Includedobservations:15afteradjustmentsVariable Coefficient Std.Errort-Statistic ProtJ.C-3373.7023^20.535-2.191761 0.0472X0.4167160.01075S38.735440.0000R-squared0.991410 Meandependeniwar1-19790.3 AdjustedR-squa.red0990750S.D.dependentvar 76921.77 SE.ofregre.ssion 7J98.292 Akaike infacriterion20.77945 Sumsquaredresid 7.12&-0S Schwarzcriterion 20.S73S6 Laglikelihood -153.84&9Hannan-Quinncrite匚20.77545 F-statistic1I3&0.435Durbin-Watsonstat 0.477498 ProbCF-statistic) a.ooaooo在回归方程中有Forecast,残差立为yfse,点击ok后自动得到下图roreestYFM J訓YForea空巾取且:20002015 AdjustedSErmpfe:2000231i mskJddd obaerratire:15Roof kter squa red Error理l%2Mean/^oLteError畐惯啟iJean Afe.PereersErro r5.451SSQThenhe鼻BI附GKWCE口.他腐4Prop&niwi□ooooooVactaree Propor^tori0.001^24G M『倚■底Props^lori09®475在上方空白处输入lsycs…之后点击proc中的forcase根据公式Y。
线性回归分析实验报告
线性回归分析实验报告线性回归分析实验报告引言线性回归分析是一种常用的统计方法，用于研究因变量与一个或多个自变量之间的关系。
本实验旨在通过线性回归分析方法，探究自变量与因变量之间的线性关系，并通过实验数据进行验证。
实验设计本实验采用了一组实验数据，其中自变量为X，因变量为Y。
通过对这组数据进行线性回归分析，我们将得到回归方程，从而可以预测因变量Y在给定自变量X的情况下的取值。
数据收集与处理首先，我们收集了一组与自变量X和因变量Y相关的数据。
这些数据可以是实际观测得到的，也可以是通过实验或调查获得的。
然后，我们对这组数据进行了处理，包括数据清洗、异常值处理等，以确保数据的准确性和可靠性。
线性回归模型在进行线性回归分析之前，我们需要确定一个线性回归模型。
线性回归模型的一般形式为Y = β0 + β1X + ε，其中Y是因变量，X是自变量，β0和β1是回归系数，ε是误差项。
回归系数β0和β1可以通过最小二乘法进行估计，最小化实际观测值与模型预测值之间的误差平方和。
模型拟合与评估通过最小二乘法估计回归系数后，我们将得到一个拟合的线性回归模型。
为了评估模型的拟合程度，我们可以计算回归方程的决定系数R²。
决定系数反映了自变量对因变量的解释程度，取值范围为0到1，越接近1表示模型的拟合程度越好。
实验结果与讨论根据我们的实验数据，进行线性回归分析后得到的回归方程为Y = 2.5 + 0.8X。
通过计算决定系数R²，我们得到了0.85的值，说明该模型能够解释因变量85%的变异程度。
这表明自变量X对因变量Y的影响较大，且呈现出较强的线性关系。
进一步分析除了计算决定系数R²之外，我们还可以对回归模型进行其他分析，例如残差分析、假设检验等。
残差分析可以用来检验模型的假设是否成立，以及检测是否存在模型中未考虑的其他因素。
假设检验可以用来验证回归系数是否显著不为零，从而判断自变量对因变量的影响是否存在。
计量经济学回归模型实验报告（大全）
计量经济学回归模型实验报告（大全）第一篇：计量经济学回归模型实验报告（大全）回归模型分析报告背景意义：教育是立国之本，强国之基。
随着改革开放的进行、经济的快速发展和人们生活水平的逐步提高，“教育”越来越受到人们的重视。
一方面，人均国内生产总值的增加与教育经费收入的增加有着某种联系，而人口的增长也必定会对教育经费收入产生影响。
本报告将从这两个方面进行分析。
我国1991 年~2013 年的教育经费收入、人均国内生产总值指数、年末城镇人口数的统计资料如下表所示。
试建立教育经费收入Y 关于人均国内生产总值指数 X 1 和年末城镇人口数 X 2的回归模型，并进行回归分析。
年份教育经费收入Y（亿元）人均国内生产总值指数X 1(1978 年=100)年末城镇人口数X 2（万人）1991 731.50282 256.67 31203 1992 867.04905 289.72 32175 1993 1059.93744 326.32 33173 1994 1488.78126 364.91 34169 1995 1877.95011 400.6 35174 1996 2262.33935 435.76 37304 1997 2531.73257 471.13 39449 1998 2949.05918 503.25 41608 1999 3349.04164 536.94 437482000 3849.08058 577.64 45906 2001 4637.66262 621.09 48064 2002 5480.02776 672.99 50212 2003 6208.2653 735.84 52376 2004 7242.59892 805.2 54283 2005 8418.83905 891.31 56212 2006 9815.30865 998.79 58288 2007 12148.0663 1134.67 60633 2008 14500.73742 1237.48 62403 2009 16502.7065 1345.07 64512 2010 19561.84707 1480.87 66978 201123869.29356 1613.61 69079 2012 28655.30519 1730.18 71182 2013 30364.71815 1853.97 73111 资料来源：中经网统计数据库。
【完整word版计量经济学实验报告多元线性回归分析 资料】计量经济学回归分析
5.79 224 23 530 6.5 142 50 8640 7.17 104 62 350 6.6 287 31 230
本文格式为 Word 版，下载可任意编辑，页眉双击删除即可。
7 41 66 1620 3.91 312 11 190 6.7 77 88 2090 4.2 142 22 900
他变量保持不变的条件下，人均 GNP1%0.005647%②统计检验
结果：
、拟合优度检验：．
图5
2R=0.707665，说明所做模型对样本数据大体上拟合不是很好，可能还
?306786864.TFP?168.1.768029FLR0.005511PGNP?12CM 回来方程式：
本文格式为 Word 版，下载可任意编辑，页眉双击删除即可。
完整 word 版计量经济学实验报告多元线性回归分析 资料】计量经济学回归分析
1、问题提出 婴儿死亡率(CM)是指婴儿出生后不满周岁死亡人数同出生人数的比率。 一般以年度为计算单位，以千分比表示。婴儿死亡率是反映一个 GJ 和民
试验 2：多元线性回来分析试验目的：学习利用 Eviews 建立多元线性 回来模型，讨论 64GJ 婴儿死亡率与妇女文盲率之间的关系。
2.指标选择 本次试验讨论婴儿死亡率与妇女文盲率之间的关系，故应接受婴儿死 亡率〔CM〕和女性识字率〔FLR〕作为指标。但影响婴儿死亡率的因素较 冗杂，尤其是经济进展状况、总生育率等也会对其产生重要影响，考虑到 试验的精确性，故引入人均 GNP〔PGNP〕和总生育率〔TFR〕相关数据。 3.数据来源 数据来源：教师提供
第1页共1页
1340 7.17 61 88 670 3.52 168 28 410 6.09 28 95 4370 2.86 121 41
计量经济学实验报告
计量经济学实验报告：马艺菡学号：4班级：9141070302任课教师：静文实验题目简单线性回归模型分析一实验目的与要求目的：影响财政收入的因素可能有很多，比如国生产总值，经济增长，零售物价指数，居民收入，消费等。
为研究国生产总值对财政收入是否有影响，二者有何关系。
要求：为研究国生产总值变动与财政收入关系，需要做具体分析。
二实验容根据1978-1997年中国国生产总值X和财政收入Y数据，运用EV软件，做简单线性回归分析，包括模型设定，模型检验，模型检验，得出回归结果。
三实验过程：（实践过程，实践所有参数与指标，理论依据说明等）简单线性回归分析，包括模型设定，估计参数，模型检验，模型应用。
（一）模型设定为研究中国国生产总值对财政收入是否有影响，根据1978-1997年中国国生产总值X和财政收入Y，如图11978-1997年中国国生产总值和财政收入（单位：亿元）1996 66850.5 7407.991997 73452.5 8651.14根据以上数据作财政收入Y 和国生产总值X的散点图，如图2从散点图可以看出，财政收入Y和国生产总值X大体呈现为线性关系，所以建立的计量经济模型为以下线性模型：（二）估计参数1、双击“Eviews”，进入主页。
输入数据：点击主菜单中的File/Open/EV Workfile—Excel—GDP.xls;2、在EV主页界面点击“Quick”菜单，点击“Estimate Equation”,出现“Equation Specification”对话框，选择OLS估计，输入““y c x”,点击“OK”。
即出现回归结果图3；参数估计结果为：Y=857.8375+0.100036iX（67.12578）（0.002172）t=（12.77955）（46.04910）2r=0.991583F=2120.520S.E.=208.5553DW=0.864 0323、在“Equation”框中，点击“Resids”,出现回归结果的图形（图4）:剩余值（Residual）、实际值(actual),拟合值（fitted）4、.（三）模型检验1.经济意义检验回归模型为：Y=857.8375+0.100036*X（其中Y为财政收入，iX为国生产总值；）所估计的参数=0.100036，说明国生产总值每增加1亿元，财政收入平均增加0.100036亿元。
计量经济学实验报告一元线性回归模型实验
2013－2014第1学期计量经济学实验报告实验（一）：一元线性回归模型实验学号姓名：专业：国际经济与贸易选课班级：实验日期：2013年12月2日实验地点：K306实验名称：一元线性回归模型实验【教学目标】《计量经济学》是实践性很强的学科，各种模型的估计通过借助计算机能很方便地实现，上机实习操作是《计量经济学》教学过程重要环节。
目的是使学生们能够很好地将书本中的理论应用到实践中，提高学生动手能力，掌握专业计量经济学软件EViews的基本操作与应用。
利用Eviews做一元线性回归模型参数的OLS估计、统计检验、点预测和区间预测。
【实验目的】使学生掌握1.Eviews基本操作：（1）数据的输入、编辑与序列生成；（2）散点图分析与描述统计分析；（3）数据文件的存贮、调用与转换。
2. 利用Eviews做一元线性回归模型参数的OLS估计、统计检验、点预测和区间预测【实验内容】1.Eviews基本操作：（1）数据的输入、编辑与序列生成；（2）散点图分析与描述统计分析；（3）数据文件的存贮、调用与转换；2. 利用Eviews做一元线性回归模型参数的OLS估计、统计检验、点预测和区间预测。
实验内容以下面1、2题为例进行操作。
1、为了研究深圳地方预算中财政收入与国内生产总值关系，运用以下数据：(1)建立深圳的预算内财政收入对GDP的回归；(2)估计模型的参数，解释斜率系数的意义；(3)对回归结果进行检验；(4)若2002年的国内生产总值为3600亿元，试确定2002年财政收入的预测值和预α=)。
测区间(0.052、在《华尔街日报1999年年鉴》（The Wall Street Journal Almanac 1999）上，公布有美国各航空公司业绩的统计数据。
航班正点准时到达的正点率和此公司每10万名乘客中投诉1(1)做出上表数据的散点图(2)依据散点图，说明二变量之间存在什么关系？(3)描述投诉率是如何根据航班正点率变化，并求回归方程。
计量经济学 简单线性回归 实验报告
实验报告1. 实验目的随着中国经济的发展，居民的常住收入水平不断提高，粮食销售量也不断增长。
研究粮食年销售量与人均收入之间的关系，对于探讨粮食年销售量的增长的规律性有重要的意义。
2. 模型设定为了分析粮食年销售量与人均收入之间的关系,选择“粮食年销售量”为被解释变量（用Y表示），选择“人均收入”为解释变量（用X 表示）。
本次实验报告数据取自某市从1974年到1987年的数据（教材书上101页表3.11），数据如下图所示：为分析粮食年销售量与人均收入的关系，做下图所谓的散点图:粮食年销售量与人均收入的散点图从散点图可以看出粮食年销售量与人均收入大体呈现为线性关系，可以建立如下简单现行回归模型：3.估计参数假定所建模型及其中的随机扰动项满足各项古典假定，可以用OLS 法估计其参数。
通过利用EViews对以上数据作简单线性回归分析，得出回归结果如下表所示：可用规范的形式将参数估计和检验的结果写为：99.61349+0.08147（6.431242）（0.10738）t= (15.48900) (7.587119)=0.827498 F=57.56437 n=144.模型检验（1）.经济意义检验所估计的参数=99.61349，=0.08147，说明人均收入每增加1元，平均说来可导致粮食年销售量提高0.08147元。
这与经济学中边际消费倾向的意义相符。
（2）.拟合优度和统计检验拟合优度的度量：由回归结果表可以看出，本实验中可决系数为0.827498，说明所建模型整体上对样本数据拟合一般偏好。
对回归系数的t检验：针对:=0 和:=0，由回归结果表中还可以看出，估计的回归系数的标准误差和t值分别为：SE()=6.431242,t()=15.48900;的标准误差和t值分别为：SE()=0.10738,t()=7.587119.取a=0.05，查t分布表自由度为n-2=14-2=12的临界值（12）=2.179.因为t()=15.48900>（12）=2.179, 所以应拒绝:=0;因为t()=7.587119>（12）=2.179.所以应拒绝:=0。
线性回归实验报告
线性回归实验报告线性回归实验报告引言：线性回归是一种常见的统计分析方法，用于研究两个变量之间的关系。
通过建立一个线性方程，我们可以预测一个变量如何随着另一个变量的变化而变化。
本实验旨在通过实际数据的线性回归分析，探讨变量之间的关系和预测能力。
实验方法：我们选择了一组与房价相关的数据进行线性回归实验。
首先，我们收集了一些房屋的特征数据，如面积、房间数量、地理位置等。
然后，我们使用这些数据来建立一个线性回归模型，以预测房价。
结果分析：通过对数据的分析和建模，我们得到了一个线性回归方程：房价 = 5000 + 50 * 面积 + 100 * 房间数量 + 200 * 地理位置。
其中，房价是我们要预测的变量，面积、房间数量和地理位置是自变量。
根据回归方程，我们可以得出以下结论：1. 面积、房间数量和地理位置对房价有显著影响。
面积和房间数量的系数分别为50和100，说明每增加一个单位的面积和房间数量，房价分别增加50和100。
2. 地理位置对房价的影响最大，其系数为200。
这意味着地理位置的变化对房价的影响更为显著，每增加一个单位的地理位置，房价增加200。
3. 房价的截距项为5000，表示当面积、房间数量和地理位置都为0时，房价的基准值为5000。
通过对回归方程的分析，我们可以根据房屋的特征数据预测其价格。
例如，如果一套房子的面积为100平方米，房间数量为3个，地理位置为2，那么根据回归方程，我们可以估计该房子的价格为：房价 = 5000 + 50 * 100 + 100 * 3 + 200 * 2 = 10,700。
讨论与结论：本实验通过线性回归分析，研究了房价与面积、房间数量和地理位置之间的关系。
通过建立回归方程，我们可以预测房价，并了解各个自变量对房价的影响程度。
然而，需要注意的是，线性回归模型的预测能力有一定的局限性。
在实际应用中，还需要考虑其他因素，如房屋的装修程度、周边环境等。
此外，线性回归模型也假设了自变量与因变量之间的关系是线性的，如果存在非线性关系，可能需要使用其他回归方法。
3 计量经济学上机实验报告-简单线性回归
实验一 简单线性回归一、 实验名称：简单线性回归 二、实验目的掌握一元线性回归模型的估计与应用，熟悉EViews 的基本操作,并且给案例做一元回归并做预测。
三、实验中所需要掌握的知识点掌握一元回归及其预测四、实验前预备的情况说明（包括上机步骤、实验所涉及的基本原理知识的复习理解、 对实验结果的预期解释等）(1)最小二乘法估计的原理 (2) t 检验 (3)拟合优度检验(4)点预测和区间预测五、上机实验内容（填写本次上机的情况）1．上机步骤⑴统计结果，如图1所示，Y ,X 的均值分别为3081.158和22225.13，Y,X 的标准差为2212.591,和22024.6图1(2) 设定模型为 12i i i Y X u ββ=++，经运算的 Equation 界面如图2图3由图2的数据得：；2．上机结果（1）回归估计结果为：Dependent Variable: Y Method: Least SquaresDate: 04/09/14 Time: 18:53 Sample (adjusted): 1978 1997Included observations: 20 after adjustmentsVariable CoefficientStd. Errort-Statistic Prob. X 0.100036 0.002172 46.04910 0.0000 C857.837567.1257812.77955 0.0000R-squared 0.991583 Mean dependent var 3081.158 Adjusted R-squared 0.991115 S.D. dependent var 2212.591 S.E. of regression 208.5553 Akaike info criterion 13.61293 Sum squared resid 782915.7 Schwarz criterion 13.71250 Log likelihood -134.1293 F-statistic2120.520 Durbin-Watson stat0.864032 Prob(F-statistic)0.000000因此得到回归模型为： Y=857.8375+0.100036X斜率系数的经济意义为：GDP 增加1亿元，财政收入增加0.1亿元。
计量经济学实验报告(范例)
在“Objects”菜单中点击“New Objects”，在“New Objects”对话框中选“Group”，并在“Name for Objects”上定义文件名，点击“OK”出现数据编辑窗口。
1．学会OLS方法的估计过程
2．掌握了模型的估计和检验方法
3．深入了解了消费函数的计量结果，扩大了思路。
一、研究目的和意义
我们研究的对象是各地区居民消费的差异。居民消费可分为城市居民消费和农村居民消费，由于各地区的城市与农村人口比例及经济结构有较大差异，最具有直接对比可比性的是城市居民消费。而且，由于各地区人口和经济总量不同，只能用“城市居民每人每年的平均消费支出”来比较，而这正是可从统计年鉴中获得数据的变量。所以模型的被解释变量Y选定为“城市居民每人每年的平均消费支出”。
若要将工作文件存盘，点击窗口上方“Save”，在“SaveAs”对话框中给定路径和文件名，再点击“ok”，文件即被保存。
2、输入数据
在数据编辑窗口中，首先按上行键“↑”，这时对应的“obs”字样的空格会自动上跳，在对应列的第二个“obs”有边框的空格键入变量名，如“Y”，再按下行键“↓”，对因变量名下的列出现“NA”字样，即可依顺序输入响应的数据。其他变量的数据也可用类似方法输入。
Annual (年度) Weekly (周数据)
Quartrly (季度) Daily (5 day week ) (每周5天日数据)
Semi Annual (半年) Daily (7 day week ) (每周7天日数据)
计量经济学实验报告完整版范文
评语
教师
评语
成绩
辽宁工程技术大学上机实验报告
实验名称
计量经济学多元线性回归模型
院系
工商管理
专业
金融
班级
09-2
姓名
于佳琦
学号
日期
6.15
实验
目的
简述本次实验目的：熟悉多元线性回归模型中的解释变量的引入
掌握对计算机过的统计分析和经济分析
实验
பைடு நூலகம்准备
你为本次实验做了哪些准备：了解多元线性回归模型参数的OLS估计，统计检验，点预测以及区间估计，非线性回归的参数估计，受约束回归检验
实验
进度
本次共有3个练习，完成3个。
实验
总结
日
本次实验的收获、体会、经验、问题和教训：在简单线性回归的基础上引入了多元线性回归模型，操作也较之前更加复杂，最大的障碍在于多重共线性模型数据更多，输入时容易出错，而且软件非汉化版本，很多时候不了解数据的含义，操作也不是很熟练，一般思路是，先用OLS方法进行估计，建立模型，然后进行对模型的检验，理论相对简单，可是检验过程十分复杂，如果不用例题做实验，单纯找数据进行分析，总会有遗忘的影响因素，而导致结果的偏差，所以在选择分析对象的影响因素时考虑周全尤为重要。
实验
进度
本次共有1个练习，完成1个。
实验
总结
日
本次实验的收获、体会、经验、问题和教训：初步投身于计量经济学，通过利用Eviews软件将所学到的计量知识进行实践，让我加深了对理论的理解和掌握，直观而充分地体会到老师课堂讲授内容的精华之所在。在实验过程中我们提高了手动操作软件、数量化分析与解决问题的能力，还可以培养我在处理实验经济问题的严谨的科学的态度，并且避免了课堂知识与实际应用的脱节。虽然在实验过程中出现了很多错误，但这些经验却锤炼了我们发现问题的眼光，丰富了我们分析问题的思路。通过这次实验让我受益匪浅。
实验报告简单线性回归分析
西南科技大学Southwest University of Science and Technology经济管理学院计量经济学实验报告——多元线性回归的检验专业班级：姓名: 学号: 任课教师: 成绩:简单线性回归模型的处理实验目的：掌握多元回归参数的估计和检验的处理方法。
实验要求：学会建立模型，估计模型中的未知参数等。
试验用软件：Eviews实验原理：线性回归模型的最小二乘估计、回归系数的估计和检验。
实验内容：1、实验用样本数据：运用Eviews软件，建立1990-2001年中国国内生产总值X和深圳市收入Y的回归模型，做简单线性回归分析，并对回归结果进行检验。
以研究我国国内生产总值对深圳市收入的影响。
经过简单的回归分析后得出表EQ1：Depe ndent Variable: Y Method: Least Squares Date: 11/27/11 Time: 14:02 Sample: 1990 2001 In cluded observati ons: 12 VariableCoefficientStd. Error t-Statistic Prob.C -3.611151 4.161790 -0.867692 0.4059 X0.134582 0.003867 34.80013 0.0000 R-squared0.991810 Mean depe ndent var 119.8793 Adjusted R-squared 0.990991 S.D. dependent var 79.361247.02733 S.E. of regressi on7.532484 Akaike infocriteri on8Sum squared resid 567.3831 Schwarz criteri on 7.1081561211.0490.00000Log likelihood-40.16403F-statisticDurbin-Wats on stat 2.051640 Prob(F-statistic)其中拟合优度为：0.991810有很强的线性关系2、实验步骤: 1、 回归分析:(1) 在 Objects 菜单中点击 New objects ，在 New objects 选择 Group ，并以GROUP01定义文件名，点击 OK 出现数据编辑窗口，， 按顺序键入数据。
计量经济学实验报告回归分析
计量经济学实验报告回归分析计量经济学实验报告：回归分析一、实验目的本实验旨在通过运用计量经济学方法，对收集到的数据进行分析，研究自变量与因变量之间的关系，并估计回归模型中的参数。
通过回归分析，我们可以深入了解变量之间的关系，为预测和决策提供依据。
二、实验原理回归分析是一种常用的统计方法，用于研究自变量与因变量之间的线性或非线性关系。
在回归分析中，我们通过最小二乘法等估计方法，得到回归模型中未知参数的估计值。
根据估计的参数，我们可以对因变量进行预测，并分析自变量对因变量的影响程度。
三、实验步骤1.数据收集：收集包含自变量与因变量的数据集。
数据可以来自数据库、调查、实验等。
2.数据预处理：对收集到的数据进行清洗、整理和格式化，以确保数据的质量和适用性。
3.模型选择：根据问题的特点和数据的特性，选择合适的回归模型。
常见的回归模型包括线性回归模型、多元回归模型、岭回归模型等。
4.模型估计：运用最小二乘法等估计方法，对选择的回归模型进行估计，得到模型中未知参数的估计值。
5.模型检验：对估计后的模型进行检验，以确保模型的适用性和可靠性。
常见的检验方法包括残差分析、拟合优度检验等。
6.预测与分析：根据估计的模型参数，对因变量进行预测，并分析自变量对因变量的影响程度。
四、实验结果与分析1.数据收集与预处理本次实验选取了某网站的销售数据作为样本，数据包含了商品价格、销量、评价等指标。
在数据预处理阶段，我们剔除了缺失值和异常值，以确保数据的完整性和准确性。
2.模型选择与估计考虑到商品价格和销量之间的关系可能存在非线性关系，我们选择了多元回归模型进行建模。
采用最小二乘法进行模型估计，得到的估计结果如下：销量 = 100000 + 10000 * 价格 + 5000 * 评价 + 随机扰动项3.模型检验对估计后的模型进行残差分析，发现残差分布较为均匀，且均在合理范围内。
同时，拟合优度检验也表明模型对数据的拟合程度较高。
线性回归分析实验报告
线性回归分析实验报告实验报告：线性回归分析一、引言线性回归是一种常用的统计分析方法，用于建立自变量与因变量之间的线性关系模型。
它可以通过对已知数据的分析，预测未知数据的数值。
本实验旨在通过应用线性回归分析方法，探究自变量和因变量之间的线性关系，并使用该模型进行预测。
二、实验方法1. 数据收集：收集相关的自变量和因变量的数据，确保数据的准确性和完整性。
2. 数据处理：对收集到的数据进行清洗和整理，确保数据的可用性。
3. 模型建立：选择合适的线性回归模型，建立自变量和因变量之间的线性关系模型。
4. 模型训练：将数据集分为训练集和测试集，使用训练集对模型进行训练。
5. 模型评估：使用测试集对训练好的模型进行评估，计算模型的拟合度和预测准确度。
6. 预测分析：使用训练好的模型对未知数据进行预测，分析预测结果的可靠性和合理性。
三、实验结果1. 数据收集和处理：我们收集了100个样本数据，包括自变量X和因变量Y。
通过数据清洗和整理，我们得到了可用的数据集。
2. 模型建立：我们选择了简单线性回归模型，即Y = aX + b，其中a为斜率，b为截距。
3. 模型训练和评估：我们将数据集分为训练集（80个样本）和测试集（20个样本），使用训练集对模型进行训练，并使用测试集评估模型的拟合度和预测准确度。
4. 预测分析：使用训练好的模型对未知数据进行预测，分析预测结果的可靠性和合理性。
四、实验讨论1. 模型拟合度：通过计算模型的拟合度（如R方值），可以评估模型对训练数据的拟合程度。
拟合度越高，说明模型对数据的解释能力越强。
2. 预测准确度：通过计算模型对测试数据的预测准确度，可以评估模型的预测能力。
预测准确度越高，说明模型对未知数据的预测能力越强。
3. 模型可靠性：通过对多个不同样本集进行训练和评估，可以评估模型的可靠性。
如果模型在不同样本集上的表现一致，说明模型具有较高的可靠性。
五、实验结论通过本实验，我们建立了一种简单线性回归模型，成功实现了对自变量和因变量之间的线性关系进行分析和预测。
计量经济学Eviews简单线性回归模型的建立与分析应用实验报告
实验一：简单线性回归模型的建立与分析应用【实验目的】1、熟悉计量经济学软件包EViews的界面和基本操作；2、掌握计量经济学分析实际经济问题的具体步骤；3、掌握简单线性回归模型的参数估计、统计检验、预测的基本操作方法；4、理解简单线性回归模型中参数估计值的经济意义。
【实验类型】综合型【实验软硬件要求】计量经济学软件包EViews、微型计算机【实验内容】为研究深圳市地方预算内财政收入（Y）与地区生产总值（X）的关系，建立简单线性回归模型，现根据深圳市统计局网站的相关信息，得到统计数据如下表：请按照下列步骤完成实验一，每个步骤要写出操作过程：（1）打开EViews，新建适当的工作文件夹；打开Eviews后，依次点击File－New－Workfile，新建一个时间序列数据（Dated-regular frequencied）类型的文件，频率选择年度（Annual），键入起止日期1990-2008（如图一），点击ok，新建工作文件夹完成（如图二）（图一）（图二）（2）在工作文件夹中新建变量X和Y，并输入数据；依次点击Objects－New Object，对象类型选择序列（Series），并输入序列名Y（如图三），点击OK，重复以上操作，新建系列对象X。
新建系列对象完成后如（图四）按住ctrl并同时选定X和Y，用鼠标右击选择open—as group，点击Edit ＋/－开始编辑，输入数据，数据输入完毕再点击Edit＋/－一次。
数据输入后如（图五）。
（图三）（图四）（图五）（3）生成X和Y的自然对数序列，保存在工作文件夹中，命名为lnX和lnY；依次点击Objects－Generate Sereies，出现Generate Series by Equation 窗口，在Enter equation窗口中输入公式：lnY=log(Y)点击ok，重复以上操作，输入：lnX=log(X) 创建序列lnX。
（如图六）（图六）（4）求X和Y的描述统计量的值，写出操作过程并画出相应表格；依次点击Quick－Group Statistics—Descriptive Statistics－Common sample，打开Series List窗口，输入x y，点击ok，输出结果（如图七）（图七）（5）作出X和Y的散点图，写出操作过程并画出相应图像，并判断模型是否接近于线性形式；依次点击Quick－Graph，打开Graph Options窗口，在Specific 中选择Scatter(散点图) （如图八）点击OK，得到散点图（如图九）（图八）由散点图可以看出模型接近线性形式（图九）（6） 用OLS 法对模型i i i u X Y ++=21ββ做参数估计，将估计结果保存在工作文件夹中，命名为eq01，写出操作过程和回归分析报告，并解释斜率的经济含义；在窗口空白处输入：ls y c x ，回车，得到结果如图回归分析报告：根据输出结果可得Ŷi = 26.02096 + 0.088820Xi (14.80278) (0.004356) t= (1.757843) (20.38986) R 2 = 0.960716 F=415.7464 D.W=0.626334 n=19 斜率的经济含义:斜率为0.088820，表示地区生产总值每增加1亿元，地方预算内财政收入平均来说增加0.088820亿元（7） 用OLS 法对模型i i i u X Y ++=ln ln 21ββ做参数估计，将估计结果保存在工作文件夹中，命名为eq02，写出操作过程和回归分析报告，并解释斜率 的经济含义；在主窗口空白处输入：ls lny c lnx ，回车，结果如图回归分析报告：根据输出结果可得lny = -1.272730 + 0.873867lnx(0.238775) (0.032394) t= (-5.330249) (26.9761) R 2 = 0.977172 F=727.7097 D.W= 0.811127 n=19 斜率的经济含义:斜率为0.873867，表示地区生产总值每增加1亿元，地方预算内财政收入平均来说增加0.0873867亿元（8） 将保存工作文件夹保存在桌面，文件名为test1.wfl ；依次点击File-Save As 将文件保存在桌面，命名为test1.wfl （9） 对eq01的估计结果做经济意义检验和统计检验（05.0=α），估计的效果如何？经济意义检验：x 的系数β2的估计值为0.088820，说明地区生产总值每增加1亿元，地方预算内财政收入平均来说增加0.088820亿元，该值处于（0,1）符合预期。
计量实验二 简单线性回归
实验二 简单线性回归（版权所有，侵权必究，未经许可，不得复制）班级：学号：姓名：一 实验目的：掌握一元线性回归的估计与应用，熟悉EViews的基本操作。
二 实验要求：应用教材P53例2.6.1与P56例2.6.2做一元线性回归分析并做预测。
三 实验原理：普通最小二乘法。
四 预备知识：最小二乘法估计的原理、t检验、拟合优度检验、点预测和区间预测。
五 实验步骤【案例1】教材P53,例2.6.1考察中国城镇居民2006年人均可支配收入与消费支出的关系。
1 建立工作文件并录入数据（1）双击桌面快速启动图标，启动Eviews5.0程序。
（2）点击主界面菜单File\New\Workfile，弹出Workfile Create对话框。
在Workfile Create对话框左侧Workfile structure type栏中选择Unstructured/Undated选项，在右侧Data Range中填入样本个数31.在右下可输入Workfile的名称，如P53。
如图2.1.1所示。
图2.1.1 图2.1.2点击左下的“OK”就建立了一个名称为P53的Workfile。
如图2.1.2所示。
图2.1.3 图2.1.4建立Workfile后，应当进行数据录入工作。
数据录入方法有多种。
这里仅介绍常用的两种录入方法。
方法1：点击主界面（或Workfile界面）的菜单栏Object，再点击New Object…选项，弹出一对话框，选择Group选项，在左侧框中命名，如为group01。
如图2.1.3所示。
点击OK之后，出现数据录入界面（以表格形式出现），如图2.1.4所示。
在图2.1.4中，先将右侧滑块拉上顶端，单击obs右侧灰色小框（空白数据列上端灰框），键入X（对样本数据列进行命名），回车（这时Workfile 中会出现序列X这个对象），选择Numeric Series选项，点击OK后，再从“1”开始逐个录入相应的数据。
计量经济学实验简单线性回归模型
计量经济学实验简单线性回归模型引言计量经济学是经济学中的一个分支，致力于通过经验分析和实证方法来研究经济问题。
实验是计量经济学中的重要方法之一，能够帮助我们理解和解释经济现象。
简单线性回归模型是实验中常用的工具之一，它能够通过建立两个变量之间的数学关系，预测一个变量对另一个变量的影响。
本文将介绍计量经济学实验中的简单线性回归模型及其应用。
简单线性回归模型模型定义简单线性回归模型是一种用于描述自变量（X）与因变量（Y）之间关系的线性模型。
其数学表达式为：Y = β0 + β1X + ε其中，Y表示因变量，X表示自变量，β0和β1为未知参数，ε表示误差项。
参数估计在实际应用中，我们需要通过数据来估计模型中的参数。
最常用的估计方法是最小二乘法（OLS）。
最小二乘法的目标是通过最小化观测值与拟合值之间的平方差来估计参数。
具体而言，我们需要求解以下两个方程来得到参数的估计值：∂(Y - β0 - β1X)^2 / ∂β0 = 0∂(Y - β0 - β1X)^2 / ∂β1 = 0解释变量与被解释变量在简单线性回归模型中，解释变量（X）用来解释或预测被解释变量（Y）。
例如，我们可以使用房屋的面积（X）来预测房屋的价格（Y）。
在实验中，我们可以根据收集到的数据来建立回归模型，并利用该模型进行预测和分析。
应用实例数据收集为了说明简单线性回归模型的应用，我们假设收集了一些关于学生学习时间与考试成绩的数据。
下面是收集到的数据：学习时间（小时）考试成绩（百分制）2 723 784 805 856 88模型建立根据收集到的数据，我们可以建立简单线性回归模型来分析学生学习时间与考试成绩之间的关系。
首先，我们需要确定自变量和因变量的符号。
在这个例子中，我们可以将学习时间作为自变量（X），考试成绩作为因变量（Y）。
然后，我们使用最小二乘法来估计模型中的参数。
通过计算，可以得到如下参数估计值：β0 = 69.85β1 = 2.95最终的回归方程为：Y = 69.85 + 2.95X预测与分析通过建立的回归模型，我们可以进行预测和分析。
线性回归法实验报告
线性回归法实验报告线性回归是一种基本的统计学方法，用来建立一个自变量和一个或多个因变量之间的线性关系模型。
其基本原理是寻找最佳的直线来拟合数据，以预测或解释因变量的数值。
本篇实验报告将介绍线性回归的基本原理和实验过程，并通过一个具体的案例进行分析和实现。
二、实验目的1. 理解线性回归的基本原理和模型；2. 掌握如何使用Python进行线性回归分析；3. 使用线性回归模型分析实际数据，并对结果进行解释和评估。
三、实验步骤1. 数据准备：选择一个合适的数据集，包括自变量和因变量。
2. 数据预处理：对数据进行清洗和归一化处理，使其符合线性回归的要求。
3. 数据分割：将数据集分为训练集和测试集，用于训练和评估模型。
4. 模型训练：使用训练集数据拟合线性回归模型。
5. 模型评估：使用测试集数据对模型进行评估，包括计算预测误差和确定模型的可靠性。
6. 结果解释和可视化：根据模型结果和评估指标，对结果进行解释和可视化展示。
四、实验案例本次实验选择一个汽车销售数据集进行分析，其中自变量为汽车的年龄和公里数，因变量为汽车的价格。
我们的目标是建立一个线性模型，以预测汽车的价格。
1. 数据准备首先，我们需要收集关于汽车价格、年龄和公里数的数据。
可以通过互联网查找相关的数据集，或者自己收集数据。
收集到数据后，可以将其保存为CSV或Excel 文件。
2. 数据预处理在进行线性回归分析之前，我们需要对数据进行预处理。
首先，对数据进行清洗，处理缺失值和异常值。
然后，对数据进行归一化处理，使其在相同的量级上。
3. 数据分割将数据集分为训练集和测试集的过程称为数据分割。
一般情况下，我们将70%的数据用于训练模型，将30%的数据用于测试模型。
4. 模型训练使用训练集数据来训练线性回归模型。
可以使用Python中的机器学习库，如scikit-learn来实现线性回归模型的训练。
5. 模型评估使用测试集数据对训练好的模型进行评估。
可以计算预测误差，如均方根误差(RMSE)和平均绝对误差(MAE)，来评估模型的预测能力。
计量经济学实验报告 回归分析
西南科技大学《计量经济学》实验报告实验项目名称：计量经济学实验指导教师：实验组成人员：学号：年级专业：【实验步骤——自己操作】一、实验数据：为了研究深圳市地方预算内财政收入与国内生产总值的关系，得到以下数据：资料来源:《深圳统计年鉴2002》，中国统计出版社(1)建立深圳地方预算内财政收入对GDP的回归模型；。
(2)估计所建立模型的参数，解释斜率系数的经济意义；(3)对回归结果进行检验；(4)若是2005年年的国内生产总值为3600亿元，确定2005年财政收入的预测值。
二、实验步骤：1.建立EViews3.1实验文件在主菜单上依次点击File/New/Work file，选择annual（年度）2.输入Y、X、T的数据在EViews软件的命令窗口键入DATA命令，命令格式为：：输入：DATA Y XLs y c x/ok 后，出现Forecast3.制图x与y的变化图形：所以根据地方预算内财政收入（Y ）和GDP 的关系近似直线关系，可建立线性回归模型：t t t u GDP y ++=21ββ4.输入命令：genr e=resid根据EViews 估计其参数结果为：t t GDP Y 134582.0611151.3ˆ+-=(4.16179) (0.003867) T = (-0.867692) (34.80013) R 2=0.99181 F=1211.049经检验说明,GDP 对地方财政收入确有显著影响。
R 2=0.99181，说明GDP 解释了地方财政收入变动的99%，模型拟合程度较好。
所以当GDP 每增长一亿元，地方财政平均收入将增长0.134582亿元。
5.回归检验——回归参数的显著性检验： 显著性检验水平：5.00=α查找自由度为n-k 的()79.122-12t 25.00=有上不检验中得出)(2k n t -≥α即为34.80013179.2≥所以在其他解释变量不变的情况下，解释变量x 对应变量y 的影响是显著的6. 若是2005年年的国内生产总值为3600亿元，确定2005年财政收入的预测值。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
实验报告
1. 实验目的
随着中国经济的发展，居民的常住收入水平不断提高，粮食销售量也不断增长。
研究粮食年销售量与人均收入之间的关系，对于探讨粮食年销售量的增长的规律性有重要的意义。
2. 模型设定
为了分析粮食年销售量与人均收入之间的关系,选择“粮食年销售量”为被解释变量（用Y表示），选择“人均收入”为解释变量（用X 表示）。
本次实验报告数据取自某市从1974年到1987年的数据（教材书上101页表3.11），数据如下图所示：
为分析粮食年销售量与人均收入的关系，做下图所谓的散点图:
粮食年销售量与人均收入的散点图
从散点图可以看出粮食年销售量与人均收入大体呈现为线性关系，可以建立如下简单现行回归模型：
3.估计参数
假定所建模型及其中的随机扰动项满足各项古典假定，可以用OLS 法估计其参数。
通过利用EViews对以上数据作简单线性回归分析，得出回归结果如下表所示：
可用规范的形式将参数估计和检验的结果写为：
99.61349+0.08147
（6.431242）（0.10738）
t= (15.48900) (7.587119)
=0.827498 F=57.56437 n=14
4.模型检验
（1）.经济意义检验
所估计的参数=99.61349，=0.08147，说明人均收入每增加1元，平均说来可导致粮食年销售量提高0.08147元。
这与经济学中边际消费倾向的意义相符。
（2）.拟合优度和统计检验
拟合优度的度量：由回归结果表可以看出，本实验中可决系数为0.827498，说明所建模型整体上对样本数据拟合一般偏好。
对回归系数的t检验：针对:=0 和:=0，由回归结果表中还可以看出，估计的回归系数的标准误差和t值分别为：SE()=6.431242,t()=15.48900;的标准误差和t值分别为：SE()=0.10738,t()=7.587119.取a=0.05，查t分布表自由度为n-2=14-2=12的临界值（12）=2.179.因为t()=15.48900>（12）=2.179, 所以应拒绝:=0;因为t()=7.587119>（12）=2.179.所以应拒绝:=0。
这表明，人均收入对粮食年销售量确有显著影响。
实验报告（多元线性回归）
1. 实验目的
随着经济的发展，人民的生活水平不断得到提高，粮食年销售量也随着增加，以某市为例，该市1974年的粮食年销售98.45万吨，而到了1987年，粮食年销售量已增加到了178.69万吨，为1974年的
1.815倍。
因此研究粮食年销售量增长的主要原因，对于分析粮食年
销售量未来的增长趋势，有很重要的经济意义，从而需要建立计量经济模型。
2. 模型设定
为了全面反映该市粮食年销售量增长的全貌，选择“粮食年销售量”为被解释变量（用Y表示），选择“常住人口”、“人均收入”、“肉销售量”、“蛋销售量”、“鱼虾销售量”作为解释变量，分别用X2、X3、X4、X5、X6表示。
本次实验数据取自某市从1974年到1987年的数据（教材书101页表3.11），数据如下图所示：
为分析被解释变量与各个解释变量之间的关系，作相关线性图形如下图所示：
从上图可以看出被解释变量和各个解释变量之间大体呈现线性关系，因此可以建立线性回归模型如下：
3. 参数估计
假定所建模型及其中的随机扰动项满足各项古典假定，可以用OLS 法估计其参数。
通过利用EViews对以上数据作多元线性回归分析，得出回归结果如下表所示：
根据以上表中数据，模型估计的结果为：
(30.00475) (0.059135) (0.037876) (1.257299) (2.450799) (2.214785)
t=(-0.116375) (2.119221) (1.945119) (2.129640) (1.409220) (-2.027920)
=0.970442 =0.951968 F=52.53043 df=14-6=8
4. 模型检验
（1）经济意义检验
模型估计结果说明，在假定其他变量不变的情况下，当常住人口每增加1万人，平均说来粮食年销售量会增加0.12532万吨；在假定其他变量不变的情况下，当人均收入每增加1元，平均说来粮食年销售量会增加0.073672万吨；在假定其他变量不变的情况下，当肉销售量每增加1万吨，平均说来粮食年销售量会增加2.677595万吨；在假定其他变量不变的情况下，当蛋销售量每增加1万吨，平均说来粮食年销售量会增加3.453715万吨；在假定其他变量不变的情况下，当鱼虾销售量每增加1万吨，平均说来粮食年销售量会减少4.491407万吨。
这与理论分析和经验判断相一致。
（2）统计检验
A．拟合优度：由回归结果表可知=0.970442 ，修正的可决系数为=0.951968。
这说明模型对样本的拟合很好。
B．F检验：针对:=====0，给定显著性水平a=0.05，在F分布中查出自由度为k-1=5和n-k=14-6=8的临界值=3.69.由回归结果表可
知F=52.53043,由于F=52.53043>=3.69,应拒绝原假设:=====0，
说明回归方程显著，即“常住人口”、“人均收入”、“肉销售
量”、“蛋销售量”、“鱼虾销售量”等变量联合起来确实对“粮食年销售量”有显著影响。
C．t检验：分别针对：=0（j=1，2，3，4，5，6），给定显著性水平a=0.05，查t分布表的自由度为n-k=8的临界值=2.306.由回归结果表中数据可知，与、、、、、对应的t统计量分别
为-0.116375、2.119221、1.945119、2.129640、1.409220、-2.027920，其绝对值均小于=2.306，说明显著性水平a=0.05的条件下，分别都应当拒绝：=0（j=1，2，3，4，5，6）也就是说在其他解释变量不变的情况下，“常住人口”、“人均收入”、“肉销售
量”、“蛋销售量”、“鱼虾销售量”分别对被解释变量都没有显著影响。