空间前方交会及其应用
空间前方交会

© 资源院 王婷婷
X NX B X X B X N X Y NY BY Y BY N Y Z NZ B Z B N Z Z Z
NX B X N X NY BY N Y NZ B N Z Z
Y
S
S
X
X
P2
a
Z Y
P1
a
A X
X
A
Y
© 资源院 王婷婷
1、模型点坐标的计算
b. 单独像对相对定向之后,模型点坐标的计算
原始数据 内方位元素 同名像点坐标
( x 0 , y0 , f )
( x1 , y1 , x2 , y2 )
0 0 相对方位元素 ( 1 , 1 , , 2 , 2 )
© 资源院 王婷婷
1、模型点坐标的计算
b. 单独像对相对定向之后,模型点坐标的计算
原始数据
计算左右片在摄测坐标系中旋转 矩阵的方向余弦
a1 b 1 c1
a1 b 1 c1
a2 b2 c2
a2 b2 c2
a3 b3 c3
a3 b3 c3
S A X Y Z S a X Y Z
SA X A X S1 YA YS1 Z A Z S1 Sa X Y Z S A X A X S 2 YA YS 2 Z A Z S 2 S a X Y Z
© 资源院 王婷婷
a2 X a1 Y b b 2 1 c2 Z c1
a3 x1 y b3 1 c3 f
武大《摄影测量》课件-第15讲空间前方交会

总结
总结本课程的重点内容和学习 收获,鼓励学习者进一步探索 和深入学习。
参考文献
- 相关文献的介绍和推荐
结束语
- 学习体会 - 空间前方交会中的定位方程,展示如何确定物 点在空间中的位置。
后方交会结果的计算
详细说明如何计算后方交会的结果,以获取精确的 物点位置。
空间前方交会的误差理论
1
后方交会误差计算
介绍后方交会误差的计算方法,帮助理解空
空间前方交会误差影响因素分析
2
间前方交会中的误差来源。
分析影响空间前方交会精度的因素,包括测
量仪器、测量方法等。
3
空间前方交会精度分析
测量空间前方交会的精度,评估定位结果的 可信度和可靠性。
空间前方交会实例分析
实例说明
通过实例解释空间前方交会的具体 应用和意义。
数据处理过程
详细描述数据处理的步骤和方法, 确保精确的测量结果。
结果分析
对测量结果进行分析和解读,探讨 应用中的可能问题和解决方案。
常见问题及解答
1 空间前方交会常见误差及解决措施
介绍常见的误差类型和对应的纠正措施,确保测量结果的准确性。
2 常见问题解答
回答学生和从业人员常问的问题,提供解答和建议。
总结
空间前方交会的应用前景
探究空间前方交会在测绘、地 理信息等领域的应用前景。
空间前方交会的发展趋势
展望空间前方交会在技术和方 法上的发展趋势,预测未来的 发展方向。
武大《摄影测量》课件-第15讲空间前 方交会
# 武大《摄影测量》课件-第15讲空间前方交会 ## 一、前言 - 空间前方交会的概念 - 空间前方交会的应用
空间前方交会基本原理
第12讲空间前方交会

S Z
Y
B
BX
a
Y X A S
Z Y
S
X
BZ
BY
a
Z
X
Y S
[二]空间前方交会公式
XYN NXYB BYX
NX NY
(5)
ZNZBZ NZ Z
Y
B
(c)
N
BX Z BZ X XZ ZX
S
BX
a
N
BX Z BZ X XZ ZX
Z
Y X A
A
Z Y
S
S BZ
X
BY
a
Z
X
Y
[二]空间前方交会公式
B
B
2 X
B
2 Y
B
2 Z
[三]模型点坐标和地面点坐标的计算过程 1、模型点坐标的计算 a. 连续像对相对定向之后,模型点坐标的计算过程
原始数据
确定角方位元素和基线分量
计算左右片在摄测坐标系中旋转 矩阵的方向余弦
a1 a2 a3
b1
b2
b3
E
c1 c2 c3
a1 a 2 a 3
b1
b 2
(X,Y,Z),(X,Y,Z)
计算投影系数 N和 N 计算模型点坐标( X,Y,Z)
X NX
Y
1 2
(NY
NY
BY
)
Z NZ
为什么Y 取中数?
X,Z?
[三]模型点坐标和地面点坐标的计算过程 1、模型点坐标的计算 a. 连续像对相对定向之后,模型点坐标的计算过程
Z Y
Z
XYNNXYBBYX
Z
BZ
N f
[二]空间前方交会公式
摄影测量-空间前交、后交【精选文档】

空间后交—前交程序设计(实验报告)姓名:班级:学号:时间:空间后交-前交程序设计一、实验目的用 C 、VB或MATLAB语言编写空间后方交会-空间前方交会程序⑴提交实习报告:程序框图、程序源代码、计算结果、体会⑵计算结果:像点坐标、地面坐标、单位权中误差、外方位元素及其精度二、实验数据f=150。
000mm,x0=0,y0=0三、实验思路1。
利用空间后方交会求左右像片的外方位元素(1).获取m(于像片中选取两点,于地面摄影测量坐标系中选取同点,分别计算距离,距离比值即为m),x,y,f,X,Y,Z(2).确定未知数初始值Xs,Ys,Zs,q,w,k(3).计算旋转矩阵R(4).逐点计算像点坐标的近似值(x),(y)(5)。
组成误差方程式(6)。
组成法方程式(7).解求外方位元素(8)。
检查是否收敛,即将求得的外方位元素的改正数与规定限差比较,小于限差即终止;否则用新的近似值重复步骤(3)-(7)2。
利用求出的外方位元素进行空间前交,求出待定点地面坐标(1).用各自像片的角元素计算出左、右像片的方向余弦值,组成旋转矩阵R1,R2(2)。
根据左、右像片的外方位元素,计算摄影基线分量Bx,By,Bz(3)。
计算像点的像空间辅助坐标(X1,Y1,Z1)和(X2,Y2,Z2)(4).计算点投影系数N1和N2(5)。
计算未知点的地面摄影测量坐标四、实验过程⑴程序框图函数AandL%求间接平差时需要的系数%%%已知%a=像点坐标x,b=像点坐标y,f内方位元素主距%φ=q,ψ=w,κ=k%像空间坐标系X,Y,Z%地面摄影测量坐标系Xs,Ys,Zsfunction [A1,L1,A2,L2]=AandL(a,b,f,q,w,k,X,Y,Z,Xs,Ys,Zs) %%%%%%%%%%%选择矩阵元素a1=cos(q)*cos(k)—sin(q)*sin(w)*sin(k);a2=-cos(q)*sin(k)—sin(q)*sin(w)*cos(k);a3=-sin(q)*cos(w);b1=cos(w)*sin(k);b2=cos(w)*cos(k);b3=—sin(w);c1=sin(q)*cos(k)+cos(q)*sin(w)*sin(k);c2=—sin(q)*sin(k)+cos(q)*sin(w)*cos(k);c3=cos(q)*cos(w);%%%%%%%共线方程的分子分母X_=a1*(X—Xs)+b1*(Y-Ys)+c1*(Z-Zs);Y_=a2*(X-Xs)+b2*(Y—Ys)+c2*(Z-Zs);Z_=a3*(X—Xs)+b3*(Y—Ys)+c3*(Z-Zs);%%%%%%%近似值x=-f*X_/Z_;y=-f*Y_/Z_;%%%%%%%A组成L组成a11=1/Z_*(a1*f+a3*x);a12=1/Z_*(b1*f+b3*x);a13=1/Z_*(c1*f+c3*x);a21=1/Z_*(a2*f+a3*y);a22=1/Z_*(b2*f+b3*y);a23=1/Z_*(c2*f+c3*y);a14=y*sin(w)-(x/f*(x*cos(k)—y*sin(k))+f*cos(k))*cos(w);a15=-f*sin(k)—x/f*(x*sin(k)+y*cos(k));a16=y;a24=—x*sin(w)-(y/f*(x*cos(k)-y*sin(k))—f*sin(k))*cos(w);a25=-f*cos(k)-y/f*(x*sin(k)+y*cos(k));a26=-x;lx=a—x;ly=b-y;%%%%%%%%%组成一个矩阵,并返回A1=[a11,a12,a13,a14,a15,a16];A2=[a21,a22,a23,a24,a25,a26];L1=lx;L2=ly;函数deg2dms%%%%%%%%角度转度分秒function y=deg2dms(x)a=floor(x);b=floor((x-a)*60);c=(x-a—b/60)*3600;y=a+(b/100)+(c/10000);函数dms2deg%%%%%度分秒转度function y=dms2deg(x)a=floor(x);b=floor((x-a)*100);c=(x-a—b/100)*10000;y=a+b/60+c/3600;函数ok%%%%%%%%%%%%%%目的是为了保证各取的值的有效值%%xy为n*1,a为1*nfunction result=ok(xy,a)format short gi=size(xy,1);for n=1:io=xy(n)—floor(xy(n,1));o=round(o*(10^a(n)))/(10^a(n));xy(n,1)=floor(xy(n,1))+o;endformat long gresult=xy;函数rad2dmsxy%%%%求度分秒表现形式的三个外方位元素,三个角度function xydms=rad2dmsxy(xy)[a,b,c,d,e,f]=testvar(xy);d=deg2dms(rad2deg(d));e=deg2dms(rad2deg(e));f=deg2dms(rad2deg(f));xydms=[a,b,c,d,e,f]';函数spacehoujiao%%%%%%%空间后交%%% f%%输入p(2*n,1)%%像点坐标x,y,X,Y,Z,均为(n,1)function [xy,m,R]=spacehoujiao(p,x,y,f,X,Y,Z)format long;%%%%%权的矢量化,这是等精度时的,如果非,将函数参数改为PP=diag(p);%%求nj=size(X,2);%%初始化Xs=0;Ys=0;Zs=0;for n=1:jXs=Xs+X(n);Ys=Ys+Y(n);Zs=Zs+Z(n);endSx=sqrt((x(2)-x(1))^2+(y(2)—y(1))^2);%%%%两像点之间距离Sd=sqrt((X(2)-X(1))^2+(Y(2)-Y(1))^2);%%%%两地面控制点之间距离m=Sd/Sx; %%%%图像比例系数Xs=Xs/j;Ys=Ys/j;Zs=m*f+Zs/j;m0=0;q=0;w=0;k=0;i=0;a=rand(2*j,6);l=rand(2*j,1);%%%%for n=1:j[a(2*n—1,:),l(2*n—1,1),a(2*n,:),l(2*n,1)]=AandL(x(n),y(n),f,q,w,k,X(n),Y(n),Z(n),Xs,Ys,Zs);enddet=inv(a’*P*a)*transpose(a)*P*l;%%%%%%%%%循环体while 1%%%%%%%%%%%%%%%%[dXs,dYs,dZs,dq,dw,dk]=testvar(det);detXs=abs(dXs);detYs=abs(dYs);detZs=abs(dZs);detq=abs(dq);detw=abs(dw);detk=abs(dk);%%%%%%%%%if ((detXs<0。
空间前方交会程序使用说明

空间前方交会程序使用说明(一)空间前方交会原理用空间前方交会法测定空间点的三维坐标常用于高精度的工业测量,例如控制装配、整机安装、轴线校正等,这些测量工作往往要求在现场快速给出大量观测点的计算结果。
空间前方交会的原理如图1所示,A 、B 为安置两台精密工业测量经纬仪(或全站仪)的测站中心点,P 1、P 2为长度L 的基准尺的两个端点。
以A 为原点,其天顶方向为Z 轴,AB 的水平方向AB′为X 轴,建立右手独立坐标系A-XYZ ;首先在测站A 、B 点分别观测基准尺两端 P 1、P 2点水平角)2,1(,=i i i βα与天顶距)2,1(,)()(=i Z Z B i A i ,以及AB 间的天顶距(AB 的高差h 未知时),计算基线AB 的长度b ,然后由A 、B 两点对各空间目标进行交会定点。
AZX图1 空间前方交会原理(二)空间前方交会计算公式1.基线尺端点的三维坐标计算若A 、B 两点基线的近似长度为0b ,则根据图1的几何关系,可导得由A 点计算P i 点三维坐标的公式为)sin(cot sin )sin(sin sin )sin(sin cos )(0)(00i i A i i A i i i i i i i i i i i Z b z b y b x βαββαβαβαβα+=+=+= (1)从B 点计算P i 点的z 坐标的公式为h Z b z i i B i i B i ++=)sin(cot sin )(0)(βαα (2)从A 、B 点测定P i 点的z 坐标之差及其平均值为:)()(B i A i i z z z -=∆ (3))(21)()(B i A i i z z z +=(4) 2.两台全站仪间的高差计算两台全站仪横轴之间的高差h 可以用瞄准大致在水平方向的同一个目标,分别用三角高程测量的方法测定其高差,按两台仪器测得高差之差计算h 。
3.测站中心点间的基线长度计算由基准尺的两个端点P 1、P 2的坐标可求得计算基准尺的计算长度为:2212212210)()()(z z y y x x L -+-+-= (5)如果基准尺水平安置,则可用下式计算;2212210)()(y y x x L -+-= (6)因基准尺精确长度L 已知,可按下式计算基线精确长度,L Lb b = (7) 4.目标点三维坐标计算求得了基线的精确长度b ,可交会计算任何目标点的三维坐标,为了便于计算器的程序编制,计算公式(1)、(2)进行改写如下:)sin(sin )sin(sin i i iB i i iA bD b D βααβαβ+=+= (8)iA i i A i D y D x ααsin cos == (9)hZ D z Z D z B i B B i A i A A i +÷=÷=)()()()(tan tan (10)(三)空间前方交会计算LISP程序设计根据空间前方交会计算的特点:(1)从两个测站向目标点观测水平角和天顶距的前方交会计算需要多次进行;(2)每个角度的“度.分秒”记录数值都需要化为弧度单位才能在LISP程序中运算;(3)读取文件中的每一行角度观测值(水平角和天顶距)均以字符形式记录,需要分段区分并作数据的类型转换。
空间后方—前方交会的原理

空间后方—前方交会的原理
以空间后方—前方交会的原理为题,我来为大家描述一下。
空间后方—前方交会是一种用于确定目标位置的方法,常用于航空、导航、测绘等领域。
它利用人眼的立体视觉和视差效应,通过观察目标在不同视角下的位置变化,来推断目标的实际位置。
这种方法可以较精确地确定目标的距离和方位,尤其适用于远距离观测。
在进行空间后方—前方交会时,我们首先需要选择两个观测点,它们之间的距离应足够远,以便产生明显的视差效应。
然后,我们分别在这两个观测点上观察目标,并记录下目标在两个观测点的位置。
接下来,我们需要测量观测点之间的距离,并确定观测点与目标之间的夹角。
这些数据将用于计算目标的实际位置。
通过对两个观测点的位置和距离进行几何分析,我们可以得到目标相对于观测点的位移向量。
然后,我们再将这个位移向量与观测点之间的夹角结合起来,就可以计算出目标相对于观测点的实际位置。
空间后方—前方交会的原理基于视差效应,即当我们观察远处的目标时,由于两只眼睛的视角不同,目标在两只眼睛中的位置也会有所不同。
通过比较这两个位置的差异,我们就可以推断出目标的实际位置。
总的来说,空间后方—前方交会是一种利用视差效应来确定目标位
置的方法。
它可以在远距离观测中提供较为准确的测量结果,具有广泛的应用前景。
前方交会投影系数法例题

前方交会投影系数法例题一、前方交会投影系数法的基本概念前方交会投影系数法是一种测量空间坐标的方法,主要用于测量地下或封闭空间中的目标点坐标。
该方法通过在观测点处设置测距仪和测角仪,测量目标点与观测点之间的水平距离和垂直距离,从而计算出目标点的空间坐标。
前方交会投影系数法具有测量精度高、操作简便等优点。
二、前方交会投影系数法的应用场景前方交会投影系数法广泛应用于地下矿山、隧道、基坑等地下工程测量,以及建筑、桥梁、水利等工程测量领域。
在这些场景中,由于观测点与目标点之间存在一定的距离和角度,采用前方交会投影系数法可以有效提高测量精度。
三、前方交会投影系数法的计算步骤1.设置观测点:在测量范围内选择合适的观测点,设置测距仪和测角仪。
2.测量水平距离和垂直距离:分别测量目标点与观测点之间的水平距离(D)和垂直距离(H)。
3.计算投影系数:根据测量得到的水平距离和垂直距离,计算前方交会投影系数(K)。
4.计算目标点坐标:利用投影系数和已知的观测点坐标,计算目标点的空间坐标。
四、常见问题及解答1.问:前方交会投影系数法适用于哪些场景?答:前方交会投影系数法适用于地下矿山、隧道、基坑等地下工程测量,以及建筑、桥梁、水利等工程测量领域。
2.问:如何提高前方交会投影系数法的测量精度?答:要提高前方交会投影系数法的测量精度,可以从以下几个方面入手:(1)选择合适的观测点和测距仪、测角仪;(2)确保测量过程中观测点、目标点之间的距离和角度准确无误;(3)采用高精度的测量仪器,如全站仪、激光测距仪等;(4)合理设置测量次数,以提高测量结果的可靠性。
3.问:前方交会投影系数法与平面坐标系的区别是什么?答:前方交会投影系数法得到的是目标点的空间坐标(三维坐标),而平面坐标系得到的是目标点的水平坐标(二维坐标)。
两者主要区别在于测量精度、应用场景和测量结果的维度。
摄影测量实验报告(空间后方交会—前方交会)
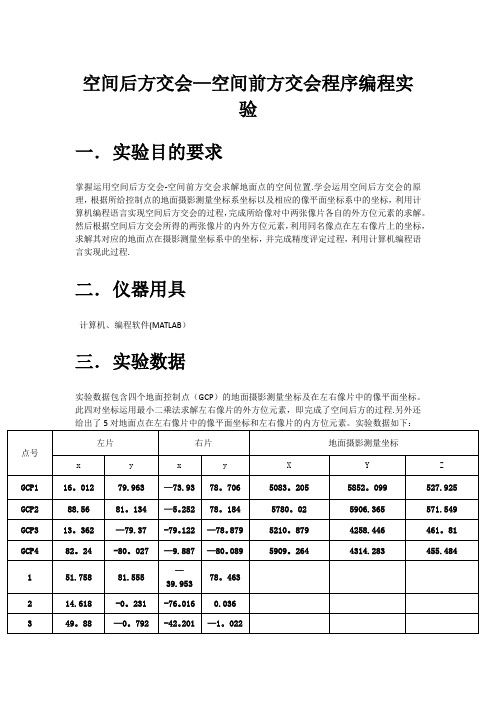
空间后方交会—空间前方交会程序编程实验一.实验目的要求掌握运用空间后方交会-空间前方交会求解地面点的空间位置.学会运用空间后方交会的原理,根据所给控制点的地面摄影测量坐标系坐标以及相应的像平面坐标系中的坐标,利用计算机编程语言实现空间后方交会的过程,完成所给像对中两张像片各自的外方位元素的求解。
然后根据空间后方交会所得的两张像片的内外方位元素,利用同名像点在左右像片上的坐标,求解其对应的地面点在摄影测量坐标系中的坐标,并完成精度评定过程,利用计算机编程语言实现此过程.二.仪器用具计算机、编程软件(MATLAB)三.实验数据实验数据包含四个地面控制点(GCP)的地面摄影测量坐标及在左右像片中的像平面坐标。
此四对坐标运用最小二乘法求解左右像片的外方位元素,即完成了空间后方的过程.另外还给出了5对地面点在左右像片中的像平面坐标和左右像片的内方位元素。
实验数据如下:内方位元素:f=152。
000mm,x0=0,y0=0 四.实验框图此过程完成空间后方交会求解像片的外方位元素,其中改正数小于限差(0。
00003,相当于0。
1'的角度值)为止。
在这个过程中采用迭代的方法,是外方位元素逐渐收敛于理论值,每次迭代所得的改正数都应加到上一次的初始值之中。
在空间后方交会中运用的数学模型为共线方程确定Xs,Ys,Zs的初始值时,对于左片可取地面左边两个GCP的坐标的平均值作为左片Xs 和Ys的初始值,取右边两个GCP的坐标平均值作为右片Xs 和Ys的初始值。
Zs可取地面所有GCP的Z坐标的平均值再加上航高.空间前方交会的数学模型为:五.实验源代码function Main_KJQHFJH()global R g1 g2 m G a c b1 b2;m=10000;a=5;c=4;feval(@shuru);%调用shuru()shurujcp()函数完成像点及feval(@shurujcp);%CCP有关数据的输入XYZ=feval(@MQZqianfangjh); %调用MQZqianfangjh()函数完成空间前方、%%%%%% 单位权中误差%%%%%后方交会计算解得外方位元素global V1 V2;%由于以上三个函数定义在外部文件中故需VV=[]; %用feval()完成调用过程for i=1:2*cVV(i)=V1(i);VV(2*i+1)=V2(i);endm0=sqrt(VV*(VV’)/(2*c-6));disp('单位权中误差m0为正负:’);disp(m0); %计算单位权中误差并将其输出显示输入GCP像点坐标及地面摄影测量坐标系坐标的函数和输入所求点像点坐标函数:function shurujcp()global c m;m=input(’摄影比例尺:');%输入GCP像点坐标数据函数并分别将其c=input('GCP的总数=');%存入到不同的矩阵之中disp('GCP左片像框标坐标:');global g1;g1=zeros(c,2);i=1;while i<=cm=input('x=');n=input('y=');g1(i,1)=m;g1(i,2)=n;i=i+1;enddisp('GCP右片像框标坐标:’);global g2;g2=zeros(c,2);i=1;while i〈=cm=input('x=’);n=input('y=’);g2(i,1)=m;g2(i,2)=n;i=i+1;end%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function shuru()global a;a=input('计算总像对点数='); %完成想计算所需的像平面坐标global b1;%坐标输入,存入不同的矩阵中b1=zeros(a,2);disp('左片像点坐标:')i=1;while i〈=am=input('x=’);n=input(’y=’);b1(i,1)=m;b1(i,2)=n;i=i+1;end%%global b2;b2=zeros(a,2);disp(’右片像点坐标:')i=1;while i〈=am=input('x=’);n=input('y=’);b2(i,1)=m;b2(i,2)=n;i=i+1;end%%global c;c=input(’GCP的总数=');disp('GCP摄影测量系坐标:’)global G;G=zeros(3,c);i=1;while i〈=cm=input(’X=');n=input(’Y=');v=input(’Z=');G(i,1)=m;G(i,2)=n;G(i,3)=v;i=i+1;end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%空间前方交会和后方交会函数:function XYZ=MQZqianfangjh()global R1 R2 a f b1 b2 Ra Rb;global X1 X2;R1=Ra;R2=Rb;R1=zeros(3,3);R2=zeros(3,3);global g1 g2 G V1 V2 V WF c QXX QXX1 QXX2;xs0=(G(1,1)+G(3,1))/2;ys0=(G(1,2)+G(3,2))/2;[Xs1,Ys1,Zs1,q1,w1,k1 R]=houfangjh(g1,xs0,ys0);%对左片调用后方交会函数R1=R;V1=V;WF1=WF;QXX1=QXX;save '左片外方位元素为。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
X 1,Y1,
Y Z Z1),( X 2, 2 , 2 ) 5.计算点投影系数 N1, 2 N 6.计算地面坐标 X , , A YA Z A
共线方程
a1 ( X X s 2 ) b1(Y Ys 2 ) c1 ( Z Z s 2 ) x2 x0 f a3 ( X X s 2 ) b3 (Y Ys 2 ) c3 ( Z Z s 2 ) a2 ( X X s 2 ) b2 (Y Ys 2 ) c2 ( Z Z s 2 ) y2 y0 f a3 ( X X s 2 ) b3 (Y Ys 2 ) c3 ( Z Z s 2 )
S1
Z1
BX= XS2 –XS1 X1
X1
ZS1 Y1 Z
(XA, YA, ZA) Y XS1 M YS1
X
像点投影系数
S1
S1 A X A X S1 YA YS1 Z A Z S1 N1 S1a1 X1 Y1 Z1
Z1
Y1
X1
S2 A X A X S 2 YA YS 2 Z A Z S 2 N2 S2a2 X2 Y2 Z2
共 线 方 程
单张像片像点坐标
地面点坐标
a1 ( X X s 2 ) b1(Y Ys 2 ) c1 ( Z Z s 2 ) x2 x0 f a3 ( X X s 2 ) b3 (Y Ys 2 ) c3 ( Z Z s 2 ) a2 ( X X s 2 ) b2 (Y Ys 2 ) c2 ( Z Z s 2 ) y2 y0 f a3 ( X X s 2 ) b3 (Y Ys 2 ) c3 ( Z Z s 2 )
前方交会定义
z1 y1 x1 S1 Z a1(x1,y1) y2 z2
由立体像对中两张 像片的内、外方位
S2
a2(x2,y2)
元素和像点坐标来
确定相应地面点在 物方空间坐标系中
x2
A(X,Y,Z) Y
坐标的方法
X
Z2
原理分析
Z1 Y1 B
Y2 X2
BZ= ZS2 –ZS1
BY= YS2 –YS1
二、计算过程(应用)
x0 ,y0, ,( X S1, S 2, S 2, 1, f Y Z Y Z 1 , 1),( X S 2,S 2, S 2, 2, 2, 2 ) 2.由外方位线元素计算基线分量 BX,BY , Z B
1.获取已知数据
3.量测像点坐标 ( x1 , y1 ),( x2 , y2 )
严密解法
x0 ,y0, ,X S , S ,Z S , , , f Y y 观测值 ( x1 , 1) , x2 , 2 ) y ( 未知数 X , Y ,Z
已知值
共线条件方程线性化
共线方程
a1 ( X X S ) b1 (Y YS ) c1 ( Z Z S ) x x0 f a3 ( X X S ) b3 (Y YS ) c3 ( Z Z S ) a2 ( X X S ) b2 (Y YS ) c2 ( Z Z S ) y y0 f a3 ( X X S ) b3 (Y YS ) c3 ( Z Z S )
第九章 解析空中三角测量的基础
河南理工大学
2008年4月19日
主要内容
一、立体像对的前方交会
二、前方交会的应用
知识回顾
单 像 片 空 间 后 方 交 会 像 片 外 方 位 元 素
A
外方位线元素: (Xs、Ys、Zs)
S
o
ZS Z Y YS
外方位角元素:
XS
、 、
X
一、立体像对前方交会
误差方程
F1 F1 F1 vx F10 X Y Z x X Y Z F2 F2 F2 v y F20 X Y Z y X Y Z
小结
1. 前方交会的原理、定义、公式的推导
2. 总结计算过程,给出严密解法
思考题
1. 推导前方交会公式? 2. 推导用最小二乘法平差的严密解算公式?
A
前方交会公式
BX Z 2 BZ X 2 N1 X 1Z 2 X 2 Z1
BX X S 2 X S 1 BY YS 2 YS 1 BZ Z S 2 Z S 1
X A X S1 N1 X 1 X S 2 N 2 X 2 1 YA [(YS1 N1Y1 ) (YS 2 N 2Y2 )] 2 Z A Z S1 N1Z1 Z S 2 N 2 Z 2
令
a1 ( X X S ) b1 (Y YS ) c1 ( Z Z S ) F1 ( X , Y , Z ) f x0 a3 ( X X S ) b3 (Y YS ) c3 ( Z Z S ) a2 ( X X S ) b2 (Y YS ) c2 ( Z Z S ) F2 ( X , Y , Z ) f y0 a3 ( X X S ) b3 (Y YS ) c3 ( Z Z S )
参考文献
1.王之卓:摄影测量原理
2.钱曾波:解析空中三角测量基础
3.李德仁:解析摄影测量学
谢谢!
X x Y y Z f
BX X S 2 X S 1 B BY YS 2 YS1 0 BZ Z S 2 Z S1 0
N1 N 2
B p
p x1 x2
B B x1 X S1 B x2 p p B B YA YS1 y1 YS1 y2 p p y1 y 2 B B Z A Z S1 f Z S 2 f q y1 y 2 0 p p X A X S1
BX Z1 BZ X 1 N2 X 1Z 2 X 2 Z1
水平像片对的前方交会公式
X x Y y Z f
BX BZ x2 f N1 p BX BZ x1 f N2 p
p x1 x2
理想像片对的前方交会公式
