ch2-4随机向量
概率论与数理统计(第3版)(谢永钦)第3章 随机向量

概率论与数理统计
定义3.7 设X和Y是两个随机变量,如果对于任意实数x和y,事
件{X≤x}与{Y≤y}相互独立,即有P{ X≤x , Y≤y }=P{X≤x}P{Y≤y},则称随 机变量X与Y相互独立。 设F(x,y)为二维随机变量(X,Y)的分布函数, (X,Y)关于X和关于Y的边缘分布 函数分别为FX(x),FY(y),则上式等价于
这正是参数为
的 分布的概率密度。
概率论与数理统计
概率论与数理统计
概率论与数理统计
概率论与数理统计
概率论与数理统计
概率论与数理统计
概率论与数理统计
X
X
Y
Y
概率论与数理统计
解: (1)串联情况
X
Y
概率论与数理统计
(2)并联情况
X
Y
感谢聆听 批评指导
概率论与数理统计
二维正态分布 若(X.,Y)的概率密度为
概率论与数理统计
4. n维随机变量
设E是一个随机试验,它的样本空间是=(e).设随机变量
是定义在同一样本空间上的n个随机变量,则称向
量
为n维随机向量或n维随机变量。简记为
设 数
为n维随机变量
是n维随机变量,对于任意实 ,称n元函数
的联合分布函数。
设(X,Y)的一切可能值为(xi,yj),i,j=1,2,… ,且(X,Y)取各对可能值的概率为 P{X=xi,Y=yj}=pij, i,j=1,2,…
称上式为(X,Y)的(联合)概率分布或(联合)分布律.离散型随机变量(X,Y) 的联合分布律可用表3-1表示.
概率论与数理统计
(X,Y)的分布律也可用表格形式表示:
记作
或记为
.
判断极性分子(向量)

一 、離子鍵、共價鍵與金屬鍵
化學鍵種類:
* 1. 實驗式又稱為簡式,僅表示出種類及其最簡整數比。 * 上述原子間作用力屬強化學鍵,還有兩種弱化學鍵-氫鍵、凡得瓦力。 離子鍵或共價鍵:氫鍵:凡得瓦力的能量≒100:10:1(僅供參考)
一 、離子鍵、共價鍵與金屬鍵
各種晶體之組成粒子及性質比較:
範例 - 1 下列各物質具有何種化學鍵? (甲) CH3OH ( 乙) H 2O (丙) NH4Cl ( 丁) P 4
(戊) HNO3
(己)金剛石
(庚) C60
(辛) SiO2
(壬) CH3CH2COONa
解答:(甲)共價鍵 (乙)共價鍵 (丙)離子鍵與共價鍵 (丁)共價鍵 (戊)共價鍵 (己)共價 (庚)共價鍵 (辛) 共價鍵 (壬)離子鍵與共價鍵
(c)對二甲苯(非極性)
例: 2-丁烯
(a)順-2-丁烯(極性)
(b)反-2-丁烯(非極性) 圖2-1-8
範例 - 3
下列何者為非極性分子? (A) H-Cl (B) O=C=O (C) (D)
解答: (B)
範例 - 4
比較下列分子極性之大小。 (A) H—Be—H (B)
甚多,極性僅為其中一種,判斷時慎用。
參考資料 一、極性共價鍵的具有永久電偶極,大小 稱為電偶極矩 (μ) 二、電偶極矩 (μ) =分子內兩原子間移轉的部分電荷 (δ)× 鍵 長 (r) ⇒ μ以德拜 (Debye,簡稱D) 為單位,δ以 庫倫 (C) 為單位。
五、分子極性大小判斷
(一) 極性分子>非極性分子
範例 - 5 下列分子或離子中何者具有極性? (1) PCl3 (5) SO2 (6) SO3 (10) CO32- (11) SO32- (2) NH3 (7) CO2 (12) SO42- (3) C2H2 (8) NO2- (4) O3 (9) NO3-
第三章-多维随机向量的分布及数字特征

xi x y j y
一般求概率函数 P ( X , Y ) ( xi , y j ) 采用以下公式: P ( X , Y ) ( xi , y j ) PX xi P Y y j X xi 例3.3 整数 X 等可能的取值1,2,3,4,整数Y 等可能的取值 1~ X,求随机向量( X , Y )的概率分布列。 解: 由题目条件随机向量( X , Y )所有可能取值点为 (1,1), (1,2), (1,3), (1,4), (2,1), (2,2), (2,3), (2,4), (3,1), (3,2), (3,3), (3,4), (4,1), (4,2), (4,3), (4,4) 显然,当 y j xi时,P ( X , Y ) ( xi , y j ) 0 。 当 y j xi时,分别有 P ( X , Y ) (1,1) P X 1 P Y 1 X 1 1 1 1 4 4 P ( X , Y ) (2,1) P X 2 P Y 1 X 2
P x1 X x2 , y1 Y y2
X
pij
0 1
Y
0
1/4 1/4
1
1/4 1/4
0 x 0或y 0 1 / 4 0 x 1且0 y 1 F ( x, y ) PX x, Y y 1 / 2 0 x 1且y 1 1 / 2 x 1且0 y 1 1 x 1且y 1
表达随机试验结果的变量个数从一个增加到两个形成二 维随机向量,概率分布律的描述有了实质的变化,而二维推 广到多维只有形式上的变化并无实质性的困难,我们主要讨 论二维随机向量。 2. 二维随机向量的分布函数 Def 设( X , Y )为二维随机向量,( x, y )为平面内任意一点,则
第二章随机向量总结

fY ( y) f 2 ( y) f ( x, y)dx
事实上, (1)f1(x)≥0, (2) 若a<b,则
b
P{a<X<b}= P{a<X<b,-∞<Y<+∞}= dx f ( x, y )dy
返回
例2.1.2.设随机变量Y~N(0,1),令
0, | Y | 1
0, | Y | 2
X 1 1,
|Y
|
, 1
X
2
1,
| Y | 2
求(X1,X2)的联合概率分布。
解:(X1,X2)的取值数对为(0,0),(0,1),(1,0),(1,1),
P(X1=0,X2=0)=P(|Y|≥1,|Y|≥2) =P(|Y|≥2) =1-P(|Y|<2) =-2Φ(2)=0.0455
i
一般地,记: P(X=xi)
Pi .
P(Y=yj)
P. j
分布表如下:
返回
Y X
y1 y2 y j
p. i.
x1 p11 p12 p1 j p1. x2 p21 p22 p2 j p2.
xi pi1 pi2 pij pi.
返回
二维联合概率分布区域图: Y
2
1
P(X≤1,Y≤1}
-1
0
P{X≥0,Y≤1}
1
X
返回
3、边缘概率分布
(1) 定义:随机向量X=(X1,X2,…,Xn)中每一个Xi的分布,称为X关
于Xi的边缘分布。
(2) 边缘分布列 对于离散型随机向量(X,Y),分量X,Y的分布列称为边缘分布列。
电子科技大学随机信号分析CH2习题及答案
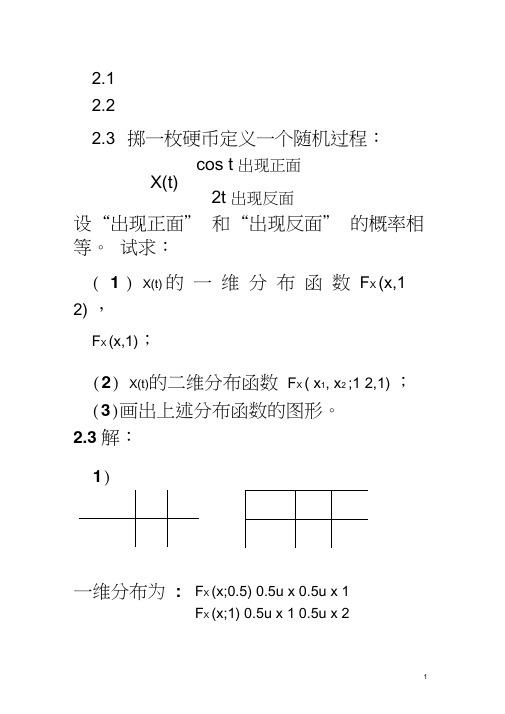
2.12.22.3 掷一枚硬币定义一个随机过程:cos t 出现正面X(t)2t 出现反面设“出现正面” 和“出现反面” 的概率相等。
试求:( 1 ) X(t) 的一维分布函数F X (x,12) ,F X (x,1);(2) X(t)的二维分布函数F X ( x1, x2 ;1 2,1) ;(3)画出上述分布函数的图形。
2.3 解:1)一维分布为:F X (x;0.5) 0.5u x 0.5u x 1F X (x;1) 0.5u x 1 0.5u x 2X (0.5) 0, X (1) 1 , 依概率 0.5发生X (0.5) 1, X (1) 2 ,依概率 0.5发生 二维分布函数为F ( x 1, x 2 ;0.5,1) 0.5u x 1,x 2 1 0.5u x 1 1,x 2 22.4 假定二进制数据序列 {B(n), n=1, 2, 3, , .} 是伯努利随机序列, 其每一位数据对 应随机变量 B(n) ,并有概率 P[B(n)=0]=0.2 和P[B(n)=1]=0.8 。
试问,( 1)连续 4 位构成的串为 {1011}的概率是 多少?(2)连续 4 位构成的串的平均串是什么?( 3)连续 4 位构成的串中,概率最大的 是(2) cos X(t) c 2o t s 出现正面出现反面什么?( 4 )该序列是可预测的吗?如果见到10111后,下一位可能是什么?2.4 解:解:(1)P 1011P B n 1 P B n 1 0 P B n 2 1 P B n 3 10.8 0.2 0.8 0.8 0.10242)设连续 4 位数据构成的串为B(n) ,B(n+1) ,B(n+2) ,B(n+3) ,n=1, 2, 3,⋯.其中B(n) 为离散随机变量,由题意可知,它们是相互独立,而且同分布的。
所以有:3k串(4bit 数据)为:X (n) 2k B(n k),k0其矩特性为:因为随机变量B(n) 的矩为:均值: E[B(n)] 0 0.2 1 0.8 0.802 0.2 12 0.8 0.8220.8 0.82 0.16 所以随机变量 X(n) 的矩为:均值:3E[X(n)] E k0332k E B(n k) 2k 0.8 12k 0 k 0方差:3k D[X(n)] D 2k B(n k) k03 2 3 2k 2 D B(n k) 4k 0.16 13.6k 0 k 0如果将 4bit 串看作是一个随机向量 , 则随机向量的均值和方差为: 串平均 :B n ,B n 1 ,B n 2 ,B n 3 0.8,0.8,0.8,0.8方差:Var B(n) Bn 2Bn 2k B(n k)串方差:Var B n ,B n 1 ,B n 2 ,B n 30.16,0.16,0.16,0.163) 概率达到最大的串为1,1,1,14) 该序列是不可预测的,因为此数据序列各个数据之间相互独立,下一位数据是0 或1,与前面的序列没有任何关系。
概率论和数理统计(第三学期)第4章随机向量

φ(x,y)=φξ(x) ·φη(y)
证明
x, y x• y
Fx, y x y u,vdudv
x
y
u
v
dudv
x
u
du
y
v
dv
F x• F y
i 1
例1 一袋中有五件产品,其中两件次品,三件正
品,从袋中任意依次取出两件,分别采用有放回与不 放回两种方式进行抽样检查,规定随机变量
=10,,
第1次取出次品 第1次取出正品
=10,,
第2次取出次品 第2次取出正品
则(ξ,η)的联合分布律如下(并可求得边缘分布律):
表1 有放回抽样的分布律
pij η
或η的概率分布称为它的边缘分布。
定义2:随机向量(ξ,η)分量ξ、η的分布函数称为(ξ,η)
关于ξ、η的边缘分布函数。
设(ξ,η)的分布函数为F(x,y) ,则(ξ,η)关于ξ的边 缘分布函数为
F x P x P{ x, } Fx,
同F理y F , y
由上述可知,Fξ(x)、Fη(y)由F(x,y)唯一确 定,但其逆并不一定成立。
(4)对任意两点(x1,y1) 、(x2,y2) ,若x1≤x2, y1≤y2,则 F(x2,y2)- F(x2,y1) - F(x1,y2)+ F(x1,y1) ≥0
§4.2 二维离散型随机向量
定义 若随机向量(ξ,η) 所有可能取值是有限对或
可列多对(xi,yj)(i,j=1,2, …),则称(ξ,η)是二 维离散型随机变量;
我们可以证明:
概率论与数理统计第3章随机向量
解 (1)根据概率密度函数性质(2)知
f (x, y)dxdy
Ce(3x4 y) dxdy C e3xdx e4y dy C 1
00
0
0
12
从而 C 1
12
(2)由定义3.3.1知
xy
F(x, y)
f (u,v)dudv
(1 e3x )(1 e4y ), x 0, y 0,
3
7
7
1
3.4.1 二维离散型随机向量的边缘分布
(2) 采取无放回摸球时,与(1)的解法相同,(X,Y)的 联合分布与边缘分布由表3.4给出.
表3.4
Y X
0
1 P{Y=yj} p j
01Biblioteka 2277
2
1
7
7
4
3
7
7
P{X=xi} pi
4 7 3 7
1
3.4.2 二维连续型随机向量的边缘分布
设(X,Y)是二维连续型随机向量,其概率密度为f(x,y),
由
FX (x) F(x,)
x
f (x,y)dydx
知,X是一个连续型随机变量,且其概率密度为
f X (x)
dFX (x) dx
f (x,y)dy.
(3.4.5)
同样,Y也是一个连续型随机变量,其概率密度为
fY ( y)
= dFY(y)
dy
f (x,y)dx.
(3.4.6)
(X ,Y )
~
N (1,
2
,
2 1
,
2 2
,
)
称(X,Y)为二维正态随机向量.
3.4 边缘分布
1 二维离散型随机向量的边缘分布 2 二维连续型随机向量的边缘分布
二维随机向量的分布
X
Y
0 1 2 3
0 0 0 1/ 8 0 3/ 8 0 0 0 3/ 8 0 0 0 0 0 1/ 8
0
X
Y
1 3
1
2
3
01 / 8 1 3/ 8 0 2 3/ 8 0 3 01/ 8
0
2019/1/6
15
三、连续型随机向量的联合密度函数
定义3
对于二维随即向量(X,Y)的分布函数 F( x, y),如果存在一个非负可积函数f (x, y) x y 使得对于 x , y R ,有 F ( x ,y ) u , v ) dud f(
F ( y ) P ( Y y ) F ( ,y ) P ( X , Y y ) Y
2019/1/6 21
例7 设二维随机变量(X,Y)的分布函数为
x y x y xy 1 e e e , x 0 , y 0 F ( x , y ) 0 , 其它 称此分布为二维指数分布,其中参数 0 .
0 第二次取到白球 Y 1 第二次取到黑球
试分别求出有放回和无放回取球情况下(X,Y)的 联合分布律。
2019/1/6 11
离散型二维随机向量联合概率分布确定方法: 1. 找出随机变量X和Y的所有取值结果,得 到(X,Y)的所 有取值数对; 2. 利用古典概型或概率的性质计算每个数 值对的概率; 3. 列出联合概率分布表.
2019/1/6
25
例9 设(X,Y)的联合概率分布表为:
X Y -1 0 1 p.j 0 0.05 0.1 0.1 0.25 1 0.1 0.2 0.2 0.5 2 0.1 0.1 0.05 0.25
3.4 随机向量的数字特征
((x EX)( yy EY )f f((x,yyddxdy x EX )( EY ) x, )) xdy
(359) (359)
一、协方差
定义38(协方差) 设 (X Y) 为 二 维 随 机 向 量 EX EY 均 存 在 如 果 E[(XEX)(YEY)]存在 则称其为随机变量X与Y的协方差 记 作cov(X Y) 即 cov(X Y)E[(XEX)(YEY)] (357) 协方差的计算 我们常常通过将(357)化简为 cov(X Y)EXYEXEY 来计算协方差
2 2 1
定理36(随机变量线性组合的方差)
设(X1 X2 Xn)是 n 维随机向量 如果 Xi (i1 2 n)的方差 均存在 则对任意实向量(1 2 n) i X i 的方差必存在 且
i 1 n
D( i X i ) 2 DX i 2 i
解 容易求得X的概率分布为 P{X0}03 P{X1}045 P{X2}025 Y的概率分布为 P{Y1}055 P{Y0}025 P{Y2}02 于是有 EX00310452025095 EY(1)0550025202015 在例320中 我们已算得EXY0 于是 cov(X Y)EXYEXEY09501501425
矩阵(ij)nn称为随机向量(X1 X2 Xn)的协方差矩阵 简称协
差阵
如果记X(X1 X2 Xn) 其协差阵通常记作DX
容易验证 对任意实向量(12 n) 有 D(X)DX 由(366)知 对任意实向量(1 2 n) (366)
注: 若cov(X,Y) = 0
X 与Y 独立
推论(随机变量和的方差)
随机向量及其分布【概率论及数理统计PPT】
n 维随机向量及其分布 由于从二维推广到n 维一般无实质性的 困难,我们重点讨论二维随机变量 .
二、二维随机向量及其分布函数
设随机试验E的样本空间是Ω。 X=X()和Y=Y()是定义在Ω上的随机变 量,由它们构成的向量(X,Y),称为二维随机向 量。 二维随机向量(X,Y)的性质不仅与X及Y的 性质有关,而且还依赖于X和Y的相互关系,因 此必须把(X,Y)作为一个整体加以研究。 为此,首先引入二维随机向量(X,Y)的分 布函数的概念。
说明
由上面的几何解释,易见: 随机点(X,Y)落在矩形区域:
x1<x≤x2,y1<y≤y2 内的概率为:
P{x1<X≤x2 ,y1<Y≤y2} =F(x2,y2)-F(x2,y1)F(x1,y2)+F(x1,y1)
其中:
这里我们介绍了二维随机向量的概念、 二维随机向量的分布函数及其性质。
二维随机向量也分为离散型和连续型, 下面我们分别讨论它们。
求:(1)X,Y的边缘分布;
(2)X+Y的概率分布.
解:(1)由分析得:
X -1
0
1
P 0.25 0.4 0.35
Y
0
1
2
P 0.25 0.5 0.25
(2)X+Y的取值为-1,0,1,2,3,
X+Y -1 0 1 2 3
P(X+Y=-1)=P(X=-1,Y=0)=0.05
P 0.05 0.2 0.4 0.3 0.05
=1
称(X,Y)服从区域D上的均匀分布。
例6. 若(X,Y)~
试求:(1)常数 A;(2) P{ X<2, Y<1}; (3) P(X≤x,Y≤y); (4)P{(X,Y)∈D},其中D为 2x+3y≤6.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
证明:由于{Y } ,于是
FX ( x ) P{ X x} P{X x,Y } lim P( X x,Y y )
y
lim F ( x,y )
y
同理可证(2-20)式成立。
定理 2-2 设 (X ,Y ) 的概率密度为 f ( x , y ) , 则关于 X 和关于Y 的边缘分布密度分别为
(4)设 G 为一平面区域,则
P{( X , Y ) G} f ( x, y )dxdy
G
特别地
P{x1 X x2 , y1 Y y2}
x2 x1
y2 y1
f ( x, y )dxdy
例 2-12 设二维随机变量 ( X ,Y )具有概率密度
Ce ( x y ) , f ( x, y) 0, x 0, y 0 其他
P{ X xi } pij ˆ pi (i 1, 2 , 3, )
P{Y y j } pij ˆ p j ( j 1, 2 , 3, )
i 1
j 1
(2-23) (2-24)来自j 1 证明: 由于 {Y y j } ,且对任意的
F ( x,y ) f (u,v ) dudv (2-16) 则称( X , Y )为二维连续型随机变量, f ( x, y ) 称为
x y
( X , Y )的概率密度或 X、Y 的联合概率密度。
f ( x, y ) 有如下性质:
(1) f ( x , y ) 0 ; (2)
(1 e x )(1 e y )
其他情况 F ( x, y ) 均为零,所以
(1 e x )(1 e y ), x 0, y 0 F ( x, y ) 0, 其他
(3) P{( X , Y ) G}
y x y 1 1 x dx 0 e x e dy 0 y 1
定义 2-6 如果( X , Y )的所有可能取值是有限个或 2, 3, ) , 可列无穷个, 记为 ( xi,y j )(i,j 1, 则称( X ,Y ) 为二维离散型 r v 。
并称
P{X xi,Y y j } ˆ pij
Distribution law
(2-14)
(i,j 1,2,3,)
数值就是随机点( X ,Y )落 在如图 2-6 所示,
y
( x, y)
以 ( x,y) 为顶点而位于左下 方的无穷矩形区域内的概率。 y
仿此解释,易得( X ,Y )落 在 ( x1 X x2,y1 Y y2 ) 内的概率为
o
( x1, y2 )
x
图 2-6
( x2 , y2 )
P{ x1 X x2,y1 Y y2}
y1 y 2 ( 对固定的 x ) F ( x, y1 ) F ( x, y 2 ) 。
(3) F ( x,y ) 关于变量 x 和变量 y 右连续,即 F ( x 0,y ) F ( x,y ) , F ( x,y 0) F ( x,y ) 。
y1 y 2 有 (4) x1 x2, F ( x2,y2 ) F ( x2,y1 ) F ( x1,y2 ) F ( x1,y1 ) 0
1 2e
1
o
0.2642
1x 图 2-7
下面介绍两种常用二维随机变量的分布:
( 1 )均匀分布
Uniform Distribution
设 G 为一平面区域,G 的面积为A (0 A ) , 若 ( X , Y ) 的概率密度为
1 / A, ( x, y ) G f ( x, y ) 其他 0,
则称( X ,Y )服从参数为 1 , 2 , 1 ( 1 0), 2 ( 2 0), ( 1) 的二维正态分布。Parameter(参数)
二维正态分布图
二维正态分布图
二维正态分布剖面图
二.边缘分布 Boundary Distribution
( X ,Y )
f ( x,y )dxdy 1 ;
f ( x, y ) 有如下性质:
(1 ) f ( x, y ) 0 ; (2 )
f ( x,y )dxdy 1 ;
(3)若 f ( x, y ) 在点( x,y ) 处连续,则 2 F ( x, y ) f ( x, y ) xy
于是(X ,Y )的概率分布表为
Y X
1 1/3 0 0
xi 2 y j 1
2 1/6 1/6 0
3 1/9 1/9 1/9
1 2 3
F (2,1) pij
1 1 1 p11 p21 3 6 2
定义 2-7 对于二维随机变量( X ,Y ),F ( x,y ) 为( X , Y )的分布函数。若存在非负可积函数 f ( x, y ) ,使对任意实数 x、y 有
k j, {Y y k }与{Y y j }互不相容, 于是得
P{ X xi } P{ X xi , {Y y j }} P{ { X xi , Y y j }}
f X ( x)
f f
( x, y )dy
( 2-21 ) ( 2-22 )
fY ( y )
( x, y )dx
x
证明: 由定理 2-1 及定义 2-7 知
FX ( x ) F ( x, )
从而
f (u,y )dudy
x y e dx 0 e dy 0
C
所以C =1 , 即
(2)由(2-16)式,当 x 0, y 0 时,
e ( x y ), x 0, y 0 f ( x, y ) 其他 0,
F ( x, y )
x u y v e du 0 e dv 0
定理 2-1 设( X,Y ) 的分布函数 F ( x,y ) ,则 关于 X 和关于Y 的边缘分布函数分别为 F X ( x ) F ( x, ) lim F ( x,y ) ( 2-19 )
y
x
FY ( y ) F ( ,y ) lim F ( x,y )
定义 2-5 设( X ,Y )为二维 r v , x、y R ,称
F ( x,y ) P{X x,Y y}
(2-12)
Y )的分布函数, 为随机向量( X , 或随机变量 X 和 Y 的
联合分布函数。
Random vectors
F ( x,y ) 在 ( x,y ) 处的函
( x1, y1 )
( x2 , y1 )
= F ( x2 , y 2 ) F ( x2 , y1 ) F ( x1, y2 ) F ( x1 , y1 ) (2-13)
o
x
F ( x,y ) 有如下性质:
1;且 (1) 0 F(x,y) 对任意固定的 y ,F ( ,y ) 0; ) 0 ; 对任意固定的 x ,F ( x, ) 0; F ( , ) 1 。 及 F ( , (2) F ( x,y ) 是变量 x 和 y 的不减函数,即 x1 x2 (对固定的y ) F ( x1,y ) F ( x2,y ) ;
( 2-20 )
定理 2-1 设( X,Y ) 的分布函数 F ( x,y ) ,则 关于 X 和关于Y 的边缘分布函数分别为
FX ( x ) F ( x, ) lim F ( x,y )
y
x
( 2-19 ) ( 2-20 )
FY ( y ) F ( ,y ) lim F ( x,y )
y
x y 1
求:(1)常数 C ; (2)分布函数 F ( x, y ) ; (3)( X ,Y )落在如图 2-7 三 角形区域内的概率。
o
1 图 2-7
x
解:(1)由于 f ( x,y )dxdy 1 ,故
1
C
( x y ) Ce dxdy 0 0
p
ij
(2-15)
例 2-11 设随机变量 X 随机地在 1,2,3 这三个整数 中任取一值,另一个随机变量Y 随机地在 1 ~ X 中任取一 整数值,试求( X ,Y )的分布律及 F (3, 2) 。
例 2-11 设随机变量 X 随机地在 1,2,3 这三个整数 中任取一值,另一个随机变量Y 随机地在 1 ~ X 中任取 1) 。 一整数值,试求( X ,Y )的分布律及 F (2, 解:(X ,Y )的可能取值为数组(1,1) , (2 ,1) , (2 , 2) , (3,1) , (3, 2) , (3, 3) , 由概率乘法公式可得 1 1 p11 P{ X 1, Y 1} P{X 1}P{Y 1 | X 1} 1 3 3
pn1 pn 2 pn 3 pnm
显然分布律pij 满足:
2, 3, ) ; (1) pij 0 (i,j 1,
(2) pij 1 。
i 1 j 1
由分布律我们可按下式求分布函数:
F ( x,y )
xi x y j y
x [
f (u,y )dy ]du
f X ( x ) FX ( x ) f ( x, y )dy
同理可证(2-22)式成立。
定理 2-3 设( X,Y ) 为离散型r.v ,其分布律为 P{ X x i, Y y j } 2, 3, ) ˆ pij (i,j 1, 则关于 X 和关于Y 的边缘分布律分别为
