关于伯德图画法的探讨
绘制伯德图
幅频和相频特性为:
A( ) (1 T 2 2 )2 (2 T )2, ( ) tg 1
1 T 1 ,o ,称为转折频率或交换频率。 T
Monday, March 09, 2015
可以用这两段渐近线近似的表示惯性环节的对数幅频特性。
3
惯性环节的Bode图
10 渐近线 0 -10 -20 0° -45° -90° 1 20T
20dB / Dec
图中,红、绿线分别是低频、高频渐近线,蓝线是实际曲线。
T
( )
2.0
-63.4
3.0
-71.5
4.0
-76
5.0
-78.7
7.0
-81.9
10
-84.3
20
-87.1
50
-88.9
100
-89.4
1 1 当 0时, (0) 0;当 时, ( ) ;当 时, () 。 T T 4 2 由图不难看出相频特性曲线在半对数坐标系中对于(0, -45°) 点是斜对称的,这是对数相频特性的一个特点。
当时间常数T 变化时,对数幅频特性和对数相频特性的形状 都不变,仅仅是根据转折频率1/T 的大小整条曲线向左或向 右平移即可。而当增益改变时,相频特性不变,幅频特性上 下平移。
Monday, March 09, 2015 6
振荡环节的频率特性
K Kn 2 ⒋ 振荡环节的频率特性: G( s) 2 2 T s 2Ts 1 s 2 n s n 2
0 L( ) 20 lg K 0 0
K 1 K 1 0 K 1
( )
180
K 0
log
5.1.15.1波德图及其绘制

40
20
0
-20
-40
-60
10-2
10-1
100
101
102
103
100
50
0
-50
-100
10-2
10-1
100
101
102
103
[mag,phase,w]=bode(A,B,C,D,w)
[mag,phase,w]=bode(A,B,C,D,iu,w) mag_dB=20*log10(mag)
将幅值转化为分贝尔 单位
波德图绘图举例1-不带返回变量
考虑如下开环传递函数 绘制其波德图曲线。
G(% Example5_1.m num=25; den=[1 4 25]; sys=tf(num,den) bode(sys);grid
图5-1 线性系统的稳态正弦响应
3
频率特性的公式表示
定义输出与输入的傅里叶变换式比值为频率特性,即
G(j)
C(j) R(j)
A
A e j
幅频特性:稳态输出与输入振幅比
A G(j)
相频特性:稳态输出与输入相位差
G(j) arg[G(j)]
4
频率特性的图解表示(三种)
1. 极坐标图(又称:幅相特性曲线,奈奎斯特图 Nyquist)
用户自定义频率步 长及范围
% Example5_2.m
num=9*[1 0.2 1];den=[1 1.2 9 0]; w=logspace(-2,3,100); [mag,phase,w]=bode(num,den,w); %mag_dB=20*log10(mag); mag_dB=mag; subplot(2,1,1);grid semilogx(w,mag_dB,'o',w,mag_dB,'-'); subplot(2,1,2);grid semilogx(w,phase,'o',w,phase,'-');
如何绘制伯德图

1
s2
K n 2 2ns n2
讨论 0 1时旳情况。当K=1时,频率特征为:
G(
j )
(1 T
1
2 2 )
j2T
幅频特征为:
A( )
1
(1 T 2 2 )2 (2T )2
相频特征为:
(
)
tg
1
1
2T T 2
2
对数幅频特征为:L() 20 log A() 20 log (1 T 2 2 )2 (2T )2
2
当 1 时,有谐振峰值。
2
M p A( p ) 2
1
1 2
由幅频特征
A( )
1
(1 T 2 2 )2 (2T )2
当
0
,A(0 )
1
2
,L(0) 20lg 2 。
所以在转折频率附近旳渐近线依不同阻尼系数与实际曲线可能
有很大旳误差。
11/29/2023
10
幅值 A()与 T 旳关系:
T 2.0 3.0 4.0 5.0 7.0 10 20 50 100
( ) -63.4 -71.5 -76 -78.7 -81.9 -84.3 -87.1 -88.9 -89.4
当 0时,(0) 0;当 1 时,( 1 ) ;当 时,() 。
T
T4
2
由图不难看出相频特征曲线在半对数坐标系中对于(0, -45°)
2
L( ) 20lg (1 T 2 2 )2 (2T )2
低频渐近线: T 1时,L() 0
高频渐近线: T 1时,L( ) 20lg (1 T 2 2 )2 (2T )2 40logT
转折频率为:o
1 T
如何绘制伯德图PPT课件

G( j ) 00
(5-63) (5-64)
100 00
900 1800
10 100 1000
图5-11 放大环节的Bode图
如图5-11所示,它是一条与角频率ω无关且与ω轴重合的直线。
5
(二)积分环节 积分环节的频率特性是
G( j) 1 j 1 1 e j90 j
7
当有n个积分环节串联时,即
dB L()
G(
j
)
(
1
j
)n
其对数幅频特性为
20 lg
G(
j )
20 lg
1
பைடு நூலகம்n
40
( 5-70 )
0
(5-71)
0.01 0.1
40 dB / dec
1
10
n 20 lg
G( j ) n 900
(5-72) 度 ()
6
设 ' 10 ,则有
20lg ' 20lg 10 20 20lg
dB L()
可见,其对数幅频特性是一条在
60
(5-68)
ω =1(弧度/秒)处穿过零分贝线 (ω 轴),且以每增加十倍频降 低20分贝的速度(-20dB/dec ) 变化的直线。
40
20dB / dec
1
L() dB
如何绘制伯德图.ppt

j?
??
其幅频特性为
1
G ( j? ) ? ?
对数幅频特性是
(5-65) (5-66)
1
20 lg G ( j? ) ? 20 lg ? ? 20 lg ? ?
(5-67)
当 ? ? 0 . 1 时,20 lg G ( j 0 . 1 ) ? ? 20 lg 0 . 1 ? 20 ( dB ) ; 当 ? ? 1 时,20 lg G ( j1) ? ? 20 lg 1 ? 0 ( dB ) ;
当 ? ? 10 时,20 lg G ( j10 ) ? ? 20 lg 10 ? ? 20 ( dB ) 。
6
设 ? ' ? 10 ? ,则有
? 20 lg ? ' ? ? 20 lg 10 ? ? ? 20 ? 20 lg ?
可见,其对数幅频特性是一条 在
dB L(? )
60
(5-68)
ω =1(弧度/秒)处穿过零分贝线
(5-73) (5-74)
? ? 20 lg 1 ? T 2? 2
当 ? ?? 1 时, 20 lg G ( j ? ) ? ? 20 lg 1 ? T 2 ? 2 ? 0 ( dB ) ,
T
当 ? ?? 1 时,20 lg G ( j ? ) ? ? 20 lg 1 ? T 2 ? 2 ? ? 20 lg T ? ( dB )
40
(ω 轴),且以每增加十倍频降
20
? 20 dB / dec
低20分贝的速度( -20dB/dec )
0
0.01
0.1
1
10
?
变化的直线。
? 20
积分环节的相频特性是
? G ( j ? ) ? ? 90 0
如何绘制伯德图

。
6
设 ' 10 ,则有
20 lg 20 lg 10 20 20 lg
'
(5-68)
dB L( )
可见,其对数幅频特性是一条在 ω =1(弧度/秒)处穿过零分贝线 ( ω 轴),且以每增加十倍频降 低 20 分贝的速度( -20dB/dec ) 变化的直线。 积分环节的相频特性是
对数幅频特性为
20 lg G( j ) 20 lg K
(5-61)
当K>1时,20lgK>0,位于横轴上方;
当K=1时,20lgK=0,与横轴重合;
当K<1时,20lgK<0,位于横轴下方。
4
放大环节的对数幅频特性如图5-11所示,它是一条与角频 率ω 无关且平行于横轴的直线,其纵坐 标为20lgK。
0
100
1000
(5-63)
180
0
放大环节的相频特性是
G( j ) 0
0
图5-11 放大环节的Bode图
(5-64) 如图5-11所示,它是一条与角频率ω无关且与ω轴重合的直线。
5
(二)积分环节 积分环节的频率特性是
G ( j ) 1 j j 1
1
e
j 90
2 2 2
(5-85)
相频特性是
G ( j ) arctg 2 1
2 2
dB
40
(5-86)20
0
1 1 10
0
精确特性
40dB / dec
二阶微分环节与振荡节的Bode
1
图关于ω 轴对称,如图5-21 。
如何绘制伯德图讲诉
-10
( )
渐近线
40dB / Dec-4
-8
1
1
1
1
2
0.8 1.0
5
10
(deg)0° -30°
10T 5T
2T
T
T
T
T
左图是不同阻尼系数情况下的
-60°
0.1
-90° 0.2
0.3
-120° 0.5
-150° 0.7
1
2T T 2
2
几个特征点: 0,() 0; 1 ,() ; ,() 。
T
2
相频特性曲线在半对数坐标中关于( 0, -90°)点是斜对称的。
这里要说明的是当 (0, 1 ) 时,() (0,90) ,当 ( 1 , )
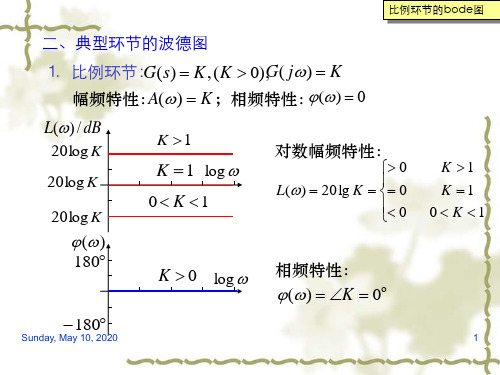
20log K
() 180
K 1
K 1 log
0 K 1
对数幅频特性:
0
L() 20lg K 0
0
K 0 log 相频特性:
() K 0
180
Thursday, May 02, 2019
K 1 K 1 0 K 1
-20
0°
-45°
-90°
1
1
1
1
1
2
5 10 20
20T 10T 5T
2T T
T
T
T
T
图中,红、绿线分别是低频、高频渐近线,蓝线是实际曲线。
Thursday, May 02, 2019
5
惯性环节的Bode图
波德图误差分析(实际频率特性和渐近线之间的误差):
4.2 伯德图法设计
用超前校正网络设计 设超前校正网络的传递函数为 K (s + z) G c (s) = 其中|z|<|p| (s + p) 设计要求是(1)系统对斜坡输入响应的稳态误差 小于10%,Kv=10;(2)系统对阶跃输入的超调量小 于10%;(3)按2%准则调节时间Ts不超过3s 根据给定的设计要求,有关公式如下
按Bode图法设计校正网络后 绘制校正后系统的Bode图 K=1800; numg=[1];deng=[1 15 50 0]; numgc=K*[1 3.5];dengc=[1 25]; [num,den]=series(numgc,dengc,numg,deng); w=logspace(-1,2,200); [mag,phase,w]=bode(num,den,w); [Gm,Pm,Weg,Wep]=margin(mag,phase,w); bode(num,den,w) title(['Gaom,argom=',num2str(Gm),'Phase margin=',num2str(Pm)]);
开环对数频率特性的一般要求
伯德图
γ = 30° ~ 60°
h > 6dB
L(dB)低频段
中频段
高频段
(1)中频段以-20dB/dec的斜率 穿越零分贝线,而且这一斜率占 有足够的频带宽度,则系统的稳 0 定性好 (2)截止频率wc越高,则系 统的快速性越好
-20dB/dec
ωc
ω
s −1
(3)低频段的斜率陡,增益高,表示系统的稳态精度好(即静差率小,调 速范围宽)
(4)高频段衰减得越快,即高频特性负分贝值 低,说明系统抗高频噪声干扰的能力越强
4.2.2 Bode图法
伯徳图的画法和在判稳中的应用
例:开环特征方程有两个右根,P=2,试判定闭环系统的稳定性。 解:
P=2
正负穿越数之差(N+-N-)为1
Z=P-2N=2-2=0 系统闭环稳定
例:开环特征方程无右根,P=0,试判定闭环系统的稳定性。 解:
P=0
正负穿越数之差为0
系统闭环稳定
§ 5.4 稳定裕度
♣ ♣ ♣
K值较小时,系统稳定; K值较大时,系统不稳定的; K取某个值时,Nyquist曲线通过 (-1,j0)点,系统处于临界稳定状态。
c ——Nyquist曲线与单位圆交点处(此处幅值为1)的 称为 截止频率(又称剪切频率),记为 c 。
G( jωc ) H ( jωc ) 1
相角裕度 180 G( jc ) H ( jc ) 含义:如果系统对频率为截止频率的信 号的相角滞后再增大 度,则系统处于临界 稳定状态。稳定系统的 > 0 , 越大,系统相 对稳定性越高。
(5) 系统开环对数相频特性表达式为
( ) arctan0.5 900 arctan arctan0.05
逐点计算结果
系统开环相频特性数据
-20dB/dec
20
-20dB/dec -40dB/dec -40dB/dec
例:
L(1) 20lg 7.5 17.5
2. Bode图上的稳定判据
闭环系统稳定的充要条件是:当ω 由0变到 +∞ 时,在开环 对数幅频特性 L(ω)≥0 的频段内,相频特性φ(ω) 穿越-π线的次 数(正穿越与负穿越次数之差)为p/2,p为s平面右半部的开 环极点数。 若开环传递函数无极点分布在S右半平面,即 P 0 , 则闭环系统稳定的充要条件是:在L(ω)≥0 的频段内,相频 特性φ(ω) 在-π线上正负穿越次数代数和为零,或者不穿越 -π线 。 Nyquist图 Bode图
控制工程基础课程中伯德图绘制的探讨
控制工程基础课程中伯德图绘制的探讨崔吉;张燕超【摘要】伯德图的绘制既是控制工程基础课程中的重点又是难点内容,学生不易理解掌握.根据多年教学经验,将高等数学分段函数思想应用在对数幅值曲线绘制中,降低了伯德图绘制的难度,便于学生理解掌握;同时又可利用分段表达式来求解剪切频率,分析闭环系统稳定性,使其更加便捷地应用于实际现场.【期刊名称】《高师理科学刊》【年(卷),期】2016(036)001【总页数】3页(P75-76,79)【关键词】伯德图;分段函数;剪切频率;稳定判据【作者】崔吉;张燕超【作者单位】中国矿业大学徐海学院,江苏徐州221000;中国石油天然气管道第二工程公司,江苏徐州221008【正文语种】中文【中图分类】TB23;G642.0在控制工程基础课程中,频率特性分析(有时也称为频率响应)是利用开环系统函数来分析闭环系统稳定的主要方法,并借助伯德图分析系统稳定性,相比劳斯代数判断更直观.频率响应有乃奎斯特图(极坐标图)和伯德图(对数坐标图)两种方法[1].两者相比,极坐标图绘制相对简单些,但精度不是很高,所以有时会影响系统闭环稳定性判断的准确性[2];伯德图绘制相对复杂些,但判断闭环系统稳定性和准确性较高,且判断稳定性原理相对简单.因此,伯德图的绘制就成为控制课程的教学重点和难点.根据多年教学实践,借助高等数学中分段函数思想,根据转折频率,将伯德图自变量划分为若干区间,然后绘制出每一区间的伯德图,进而得到整体伯德图.使学生既懂得了伯德图的绘制,又掌握了利用伯德图判断系统的稳定性及剪切频率等性能参数的计算,极大地提高了教学效果.1 利用分段函数绘制伯德图学生不容易掌握伯德图绘制的原因有两个[3]:一是求解频率特性的幅频和相频;二是如何建立对数坐标系.虽然借助MATLAB等软件可以比较简单地绘制出伯德图[4],但要让学生掌握伯德图思想就需要把这些内容介绍清楚.选用董景新主编的《控制工程基础》[5]为教材,书中先介绍了典型环节的伯德图绘制;开环传递函数伯德图则要将系统频率特性化为典型环节频率特性的乘积,这里要强调的一定要换成标准的典型环节;然后求解出各个典型环节的幅值和转折频率,最后依照转折频率的大小依次画出伯德图.概括为“先比例后积分然后按照转角频率的大小依次叠加”[6].根据伯德图绘制的方法,按照转角频率将横坐标划分为几个区间,整个伯德图表达式就可以变换成分段函数,然后按照区间段来绘制每个表达式,这样学生就容易绘制幅值的伯德图.2绘制伯德图的实例通过文献[5]第267页例题来介绍绘制步骤,开环函数为.(1)将转换为,则变为.(2)换成标准形式.由于该表达式已经为标准式,无需再变换,这一步骤要给学生着重强调.(3)求出每个典型环节的转折频率以及斜率.根据转折频率可以将自变量分割为(0,25],(25,100],(100,∞),则幅值的对数表达式为根据分段函数表达式,幅值对数伯德图很容易绘制出(见图1).但绘制幅值伯德图时,可用分段直线来代替曲线,便于在工程现场大致分析系统性能.为保证图形的连续性,利用分段函数表达式,前一段直线的终点可认为是后续区间段的起点.利用这个分段函数,也可以在不绘制伯德图情况下求出剪切频率.剪切频率可以看作是幅值对数伯德图与零分贝线的交点,利用分段函数的区间段求出极值.这样就可以判断在哪个区间段存在剪切频率,然后令该区间的函数值为0,求出剪切频率[7-8].在上述实例中第1段最小值为12 dB,第2段最小值则为-12 dB,因此剪切频率判断出在第2区间内.令第2分段函数的值为0,即可求解剪切频率值为50 rad·s-1.此外,利用相位裕量,也可大致判断系统的稳定性.将剪切频率带入相频表达式中得到:很显然,系统临界稳定.与教材[5]的判断结果一致.通过具体实例可以看出,分段函数在伯德图绘制中起到很大的作用,既方便学生理解伯德图的含义,同时还可以在不绘制出幅值和相频伯德图的前提下,大致判断出系统的稳定性.[1] 彭珍瑞,董海棠.控制工程基础[M].北京:高等教育出版社,2010[2] 方斌.关于Bode图稳定判据与稳态误差级数的讨论[J].信息与控制,1999,28(4):293-296[3] 张翠平.浅谈《控制工程基础》的几点教学体会[J].长春理工大学学报:高教版,2009,4(1):191-192[4] 张琳.MATLAB与控制系统的频域分析[J].邢台职业技术学院学报,2011,28(1):86-88[5] 董景新.控制工程基础[M].2版.北京:清华大学出版社,2003[6] 李增权,马静婕.关于伯德图画法的探讨[J].内蒙古电大学刊,2005(4):56-59[7] 谢丽蓉,程静,玛依拉,等.控制系统稳定性判别的虚拟平台设计[J].工业和信息化教育,2014(5):81-82,90[8] 张正强.在伯德图上求截止频率的一种解析方法[J].电气电子教学学报,2009(31):31-33。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
关于伯德图画法的探讨
李增权马静婕
(河南质量工程职业学院,河南平顶山467000)
在应用频率特性研究系统性能过程中,先后提
出了用极坐标图表示(又称奈式图)和用对数坐标
图表示(又称伯德图)的方法。
由于前者图形绘制
麻烦,而且不够直观,故大多采用伯德图的方法来
研究,所以,伯德图就成了研究系统性能的关键环
节,伯德图的画法,在自动控制教学中就成了一贯
的重点和难点。
下面根据自己的教学经验,对如何
画伯德图这部分教学谈一些体会。
在我们采用的上海机械高等专科学校孙凡才
编的5自动控制原理与系统6这本书里,这一部分教
学是首先讲解典型环节的对数频率特性,从而可采
用叠加的方法求串联环节的伯德图,而系统的开环
传递函数通常为反馈回路中各串联环节的传递函
数的乘积,故对系统的开环频率特性,我们就很容
易得到,继而书中又提出了对数幅频特性的一种简
便画法,其步骤是:
(1)分析系统是由哪些典型环节串联而成的,
将这些典型环节的传递函数都分成标准形式。
(2)根据比例环节的K值,计算20lgK。
(3)在半对数坐标纸上,找到横坐标为X=1,
纵坐标为L(X)=20lgK的点,过该点做出斜率为
-20VdB/dec的斜线,其中V为积分环节的数目。
(4)计算各典型环节的交接频率,将各交接频
率按由低到高的顺序进行排列,并按下列原则依次
改变L(X)的斜率:
若过惯性环节的交接频率,斜率减去20dB/
dec;
若过比例环节的交接频率,斜率增加20dB/
dec;
若过振荡环节的交接频率,斜率减去40dB/
dec。
(5)如果需要,可以对渐进线进行修正,以获得
较准确的对数幅频特性曲线。
例:某系统的开环传递函数:
G(s)=150@1
s2@1
0.02s+1
@(0.1s+1)
由上式可见,它是由比例节、两个积分环节、一
个惯性环节和一个比例微分环节串联组成的。
1.对数幅频特性
(1)低频段的绘制:由K=150,故L(X)在X=1
处的高度为20lgK=20lg150=43.5dB,由于含有两
个积分环节,其低频段斜率为:
2@(-20dB/dec)=-40dB/dec。
(2)中、高频段的绘制
比例微分环节的交接频率
X1=1/0.1s=10rad/s
惯性环节的交接频率
X2=1/0.02s=50rad/s
因此,在低频段为-40dB/dec的斜直线,经X1=
10处遇到比例微分环节,应增加20dB/dec,成为-
20dB/dec的直线,再经X2=50处,又遇到一惯性环
节,则应降低-20dB/dec,又成为-40dB/dec的斜线。
因此,该系统的对数幅频特性如下图(a)所示
:
2.对数相频特性
比例环节:51(X)=0水平直线¹
两个积分环节:52(X)=-180b水平直线º
比例微分环节:53(X)=tg-10.1X,曲线»低频
渐进线为:5(X)=0,高频渐进线为:5(X)=+90b,
在X=10rad/s处,53(X)=45b。
惯性环节:54(X)=-tg-10.02X,曲线¼其低
频渐进线为:5(X)=0,高频渐进线为:5(X)=-
90b,在X=50rad/s处,54(X)=-45b,该系统的对数
相频特性5(X),则为四者的叠加,即:5(X)=51(X)
+52(X)+53(X)+54(X)(下转第59页)
)
50
)
林勇平基层电大校本培训的实践与反思教育教学研究
间,对社会动态反映敏感而快速;(7)学分制管理、按课程注册学习,学生学习呈个别化趋势;(8)学习手段、方式、时间出现明显的变化;(9)学生与学校(教师、管理人员)处于准分离状态,校园氛围影响甚小。
因此,电大必须根据学生的上述特点,结合专业课程教学,在实施专业培养目标过程中开展素质教育。
2.精心做好专业教学计划和课程体系的设计。
专业教学计划是培养人才的一个具体规划,他具体明确了专业人才培养的规格和目标;而课程体系是指根据专业人才的培养的规格和目标,将应该学习的相互联系而又相互制约的相关课程组成一个有机整体,它是专业教学计划的主体,也是人才培养的规划图。
长期以来,困扰中国高等教育发展的最主要因素之一,就是高等教育的课程体系陈旧,课程内容落后。
而不同类型的学校,不同的规格层次,不同的培养对象,使用的却是类似的课程体系和课程内容,包括类似的教学方法,这很难真正有效地开展素质教育。
3.通过更新课程内容,有效地提高专业技能素养。
作为以成人在职学生为主要教育对象的广播电视大学教育,应该强化学生的应用型人才培养教育。
专科层次的学历教育,其本质就是高等职业教育。
因此,我们在制定专业教学计划时,在确保基础理论/必要与够用0的前提下,不断调整和更新课程教学内容,增加内容的实用性与可操作性的比例。
财务报表解释、法律基础与实务、证券投资分析、电子商务应用、实用文体写作等一大批实用性课程,在对学生实际动手能力培养中发挥了重要作用。
除此以外,我们还要根据远程教育的实际情况,开辟网上模拟炒股实验室、远程实验装置等实验项目,以此来提高学生的实际动手能力。
另外还应根据各地的实际、用人行业的现实需求,开设适合当地的实用型专业,比如社区管理等。
这样将学历教育与用人单位迫切需要的岗位培训、证书教育有机地结合,有效地开辟培养行业急需人才与培养专科应用型人才的贯通途径,得到了社会的肯定。
[责任编辑:陈维廉]
(上接第50页)如下图(b)所示
:
但是对于系统的开环对数幅频特性的简便画法并不是适用于每一个系统。
因为,这种简便画法有两个前提,即:
¹L(X )|X =1=20lgK 。
º各典型环节的交接频率都大于1rad/s 。
如不能满足这些条件,就不能直接用简便画法。
例:某系统的开环传递函数为:
G(s)=4@1s
2@1
2s+1@(0.5s+1)
由上式可见,它是由¹一个比例环节;º一个积分环节;»一个惯性环节;¼一个比例微分环节串联组成。
其中»、¼的交接频率为:X 3=0.5,X 4=2。
我们按各个环节相叠加的方法来画它的对数幅频特性曲线步骤为:
¹L 1(X )的幅值为20lg4=12dB 平行于X 轴水
平线。
ºL 2(X )斜率为-20dB/dec 的斜线,它与X 轴交于X =1处。
»L 3(X )在X <X 1=0.5内是一条0dB 直线;X >X 1时是一条斜率为-20dB/dec 的直线。
¼L 4(X )在X <X 2=2内是一条0dB 直线;X >X 2=0.5时是一条斜率为+20dB/dec 的直线。
½L 1(X )V L 4(X )叠加即可求得开环对数幅频特性曲线L (X )。
由上图C 可见L (X )|X =1=20Lg4=12dB,故不能使用简便画法。
这在课本中没有特意指出,会使学生误认为任何系统的开环幅频特性曲线均可用简便画法画出。
这里说明一下,供大家参考。
[责任编辑:张建荣]
)
59)李永利 远程教育构建终身学习体系的实现形式 教育教学研究。
