中内讲义-37
人像摄影03-37.3 三分面人像课程讲义_37

Chapter 3 人像摄影的构图技巧107 47 三分面人像有时,当被摄主体存在缺陷或不足时,我们需要变换角度,来“美化”主体,将好的一面展现出来,或者为主体“瘦身”,三分面人像可以达到这种效果。
三分面人像是指被摄者比七分面的拍摄角度更侧转一点。
从照相机的方向虽然仍能看到被摄者脸部的正面,但正面所占的比例不如侧面大,脸部同相机镜头成 60°左右角度。
1.画面特点在这种视图中,离镜头远的那只耳朵看不到,能看到的脸的一侧也比另一侧多得多。
与七分面人像相比,在三分面人像中,面部较窄的那面的轮廓线条更鲜明、更突出;而且,鼻梁的高低更加明显,面部较宽的侧面的线条轮廓在视觉上就显得不那么突出了。
图片说明:这幅照片在室外拍摄,结合逆光,凸显模特享受阳光的可爱一面。
三分面的运用使模特更富有立体感。
拍摄数据:光圈F4,快门速度1/125秒,I S O320,焦距为50mm。
÷分面人像张ᯯ心摄和七分面人像一样,如果有的被摄者脸部两侧的轮廓线条不十分对称,在拍摄时便可以让其转向轮廓好看的一侧,使略有缺陷的一侧处在不太突出的部位。
例如,根据近大远小的透视原理,离镜头远的那只眼睛会显得小一些。
所以,如果模特一只眼睛比另一只稍小,可以把小的那只眼睛置于靠近镜头的位置,由于透视原理,两只眼睛看起来就一般大了,类似的,嘴巴、脸颊都可以按此原则矫正大小。
所以,一般来说,三图片说明:拍摄时注意不要使人物脸部失去细节,在人物正面补光时调整好角度, 使反光板同时完成眼神光的任务。
这幅照片为了增加画面动感和趣味性,使模特的领结飘起。
拍摄数据: 光圈F8,快门速度 1/125 秒, IS O 100,焦距为 36mm 。
108 光影解密——提高人像摄影水平的80个关键点分面人像能有效地改善、美化人物主体自身存在的缺陷和不足;另外,如果人物主体体型较胖,采用这种角度,常能达到明显的“减肥”效果。
三分面人像不适合所有脸型的人,如对于颧骨高耸的人,就不太适合。
高考数学复习知识点讲义课件34---任意角

知结构体系
(一)任意角 1.角的定义及分类 (1)角的概念:角可以看成平面内一条 射线绕着它的端点 旋转所成的图形 . (2)角的表示:如图所示,角α可记为“α”或“∠α”或“∠AOB”, 始边: OA ,终边: OB ,顶点 O .
(3)角的分类
名称 正角 负角 零角
定义 一条射线绕其端点按 逆时针 方 向旋转形成的角 一条射线绕其端点按 顺时针 方 向旋转形成的角 一条射线 没有 做任何旋转形成 的角
A.120°+k·360°,k∈Z
B.120°+k·180°,k∈Z
C.240°+k·360°,k∈Z
D.240°+k·180°,k∈Z
(2)下列角的终边与37°角的终边在同一直线上的是
A.-37°
B.143°
C.379°
D.-143°Biblioteka () ()[解析] (1)角2α与240°角的终边相同,则2α=240°+k·360°,k∈Z,则α= 120°+k·180°,k∈Z.
(二)象限角与终边相同的角 1. 象限角与终边相同的角
把角放在平面直角坐标系中,使角的顶点与 原点 重合,角的始 象 边与x轴的非负半轴重合,那么,角的 终边 在第几象限,就说 限 这个角是第几 象限角 ;如果角的终边在 坐标轴上 ,就认为这
角 个角不属于任何一个象限
终边 所有与角α终边相同的角,连同角α在内,可构成一个集合S= 相同 {β|β=α+k·360°,k∈Z},即任一与角α终边相同的角,都可以表 的角 示成角α与整数个周角的和
答案:D
3.2 020°是
()
A.第一象限角
B.第二象限角
C.第三象限角
D.第四象限角
解析:2 020°=5×360°+220°,所以2 020°角的终边与220°角的终边相同,为 第三象限角.
第37课 有孔纸片托水-讲义-小学社团科学实验课后服务

有孔纸片托水
同学们,思考:有孔的纸为什么能拖住水?
准备器材:
瓶子一个、大头针一个、纸片一张,有色水一满杯
操作步骤:
1.在空瓶内盛满有色水。
2.用大头针在白纸上扎许多孔。
3.把有孔纸片盖住瓶口。
4.用手压着纸片,将瓶倒转,使瓶口朝下。
5.将手轻轻移开,纸片纹丝不动地盖住瓶口,而且水也未从孔中流出来。
大博士解谜科学原理:
薄纸片能托起瓶中的水,是因为大气压强作用于纸片上,产生了向上的托力。
小孔不会漏出水来,是因为水有表面张力,水在纸的表面形成水的薄膜,使水不会漏出来。
这如同布做的雨伞,布虽然有很多小孔,仍然不会漏雨一样。
中公辅导班内部讲义之公务员考试常识大全[一].
![中公辅导班内部讲义之公务员考试常识大全[一].](https://img.taocdn.com/s3/m/cfdc443ebb68a98271fefa50.png)
公务员考试常识大全[一] 栏目树形导航站点首页文章中心下载中心图书中心考试论坛雁过留声 VIP 申请当前位置:公务员在线 > 文章中心 > 模拟题库> 公共基础 > 文章正文公务员考试常识大全[一] 1. 《嘎达梅林》是哪个民族的叙事歌曲? (高级题 1 藏族 2 满族 3 蒙古族 4 回族 2. 我国的第一部诗歌总集是: (低级题 1诗经 2 女神-- 3. 在我国内地驾驶车辆,必须遵守: (中级题 1 左侧通行的原则 2 右侧通行的原则 4. 围棋棋盘共有几个交*点? (低级题 1)360 2)361 5. 人体最大的细胞是: (低级题 1:卵细胞 2 脑细胞 3 淋巴细胞 6. 被称为我国最最大的古典艺术宝库的石窟是哪一个? (中级题 1 甘肃敦煌莫高窟 2 新疆千佛洞 3 四川乐山大佛 7. 下面哪座山是中国佛教四大名山之一? (高级题 1峨嵋山 2 华山 3 泰山 4 嵩山8. 人体最坚硬的部分是: (中级题 1 指甲 2:牙齿 3 颅骨 9. 以下哪一种商品的需求价格弹性最小? (低级题 1 粮食 2 食盐 10. "海市蜃楼"现象在不同时间内出现的影像不同,有时候是影像呈正象,有时候是影像呈倒象,请问呈倒象的是什么时段 (低级题 1下午时段 2 上午时段 -- 11. 被称为"国际会议之都"的城市是: (低级题 1 日内瓦 2 华盛顿 12. 我国最大的淡水湖是: (高级题 1 洞庭湖 2鄱阳湖 3 太湖 4 哈纳斯湖 13. 哪个国家是钻石的最大产出国?(吗) (中级题 1扎伊尔 2 刚果 3 南非 14. 好莱坞位于美国什么州: (低级题 1加利福尼亚州 2 阿拉斯加洲 15. "席梦思"三个字源于什么? (低级题1 地名 2 人名 16. 沙漠之舟--骆驼的驼峰是用来 (低级题 1 贮水的 2贮脂肪的 3 驮物品的 17. 参加第一届古代奥运会的国家有: (中级题 1:三个2 四个 3 五个 18. 股票市场中指数大幅上升又称: (低级题 1牛市 2 熊市 19. <<义勇军进行曲>>是哪部电影的主题歌? (高级题 1 《英雄儿女》 2《风云儿女》3 《平原游击队》 4〈〈永不消逝的电波〉〉 20. 水上芭蕾又称: (低级题 1 自游泳 2花样游泳--- 21. 海马是马吗? (低级题 1 不是 2 是- 22. UNESCO是什么国际组织的简称? (中级题 1 联合国科教文组织 2 联合国安理会 3 世界卫生组织 23. 发射第一颗人造卫星的国家是: (低级题 1美国 2 前苏联-- 24. "艾叶"燃烧的烟能驱蚊蝇,对吗? (低级题 1 对 2 不对-- 25. 鱼有心脏吗? (低级题 1有(脊椎动物都有心脏。
中考数学解题大招复习讲义(全国通用)模型02 飞镖、8字模型(解析版)
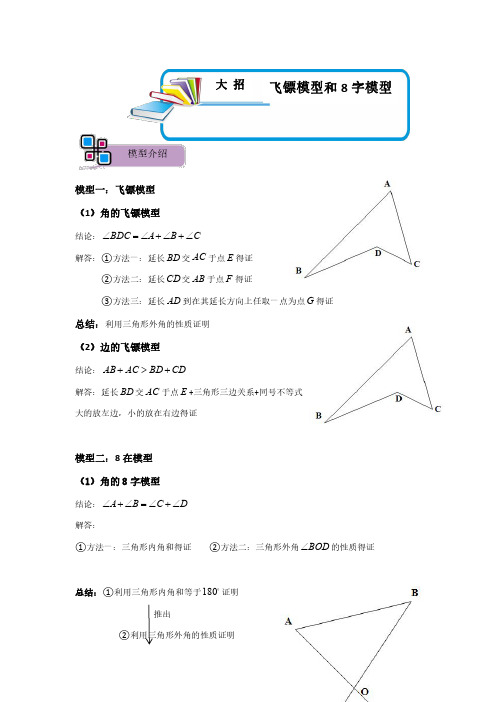
模型介绍模型一:飞镖模型(1)角的飞镖模型结论:CB A BDC ∠+∠+∠=∠解答:①方法一:延长BD 交AC 于点E 得证②方法二:延长CD 交AB 于点F 得证③方法三:延长AD 到在其延长方向上任取一点为点G 得证总结:利用三角形外角的性质证明(2)边的飞镖模型结论:CDBD AC AB +>+解答:延长BD 交AC 于点E +三角形三边关系+同号不等式大的放左边,小的放在右边得证模型二:8在模型(1)角的8字模型结论:DC B A ∠+∠=∠+∠解答:①方法一:三角形内角和得证②方法二:三角形外角BOD ∠的性质得证总结:①利用三角形内角和等于180证明推出②利用三角形外角的性质证明大招飞镖模型和8字模型(2)边的8字模型结论:BCAD CD AB +<+解答:三角形三边关系+同号不等式得证总结:①三角形两边之和大于第三边例题精讲考点一:飞镖模型【例1】.如图,∠A =70°,∠B =40°,∠C =20°,则∠BOC=_______解:延长BO ,交AC 于点D ,∵∠BOC =∠C +∠ODC ,∠ODC =∠A +∠B ,∠A =70°,∠B =40°,∠C =20°,∴∠BOC =∠C +∠A +∠B=20°+70°+40°=130°.变式训练【变式1-1】.如图,∠ABD 、∠ACD 的角平分线交于点P ,若∠A =55°,∠D =15°,则∠P 的度数为()A.15°B.20°C.25°D.30°解:如图,延长PC交BD于E,∵∠ABD,∠ACD的角平分线交于点P,∴∠1=∠2,∠3=∠4,由三角形的内角和定理得,∠A+∠1=∠P+∠3①,在△PBE中,∠5=∠2+∠P,在△DCE中,∠5=∠4﹣∠D,∴∠2+∠P=∠4﹣∠D②,①﹣②得,∠A﹣∠P=∠P+∠D,∴∠P=(∠A﹣∠D),∵∠A=55°,∠D=15°,∴∠P=(55°﹣15°)=20°.故选:B.【变式1-2】.在△ABC中,∠ABC与∠ACB的平分线交于点I,∠ABC+∠ACB=100°,则∠BIC的度数为()A.80°B.50°C.100°D.130°解(1)∵∠ABC与∠ACB的平分线交于点I,∴∠BCI=∠ACB,∠CBI=∠ABC,∴∠BIC=180°﹣∠BCI﹣∠CBI=180°﹣100°=130°;故选:D.【变式1-3】.如图,已知∠BOF=120°,则∠A+∠B+∠C+∠D+∠E+∠F的度数.解:如图,根据三角形的外角性质,∠1=∠A+∠C,∠2=∠B+∠D,∵∠BOF=120°,∴∠3=180°﹣120°=60°,根据三角形内角和定理,∠E+∠1=180°﹣60°=120°,∠F+∠2=180°﹣60°=120°,所以,∠1+∠2+∠E+∠F=120°+120°=240°,即∠A+∠B+∠C+∠D+∠E+∠F=240°.【变式1-4】.如图所示,已知P是△ABC内一点,试说明PA+PB+PC>(AB+BC+AC).证明:在△ABP中:AP+BP>AB.同理:BP+PC>BC,AP+PC>AC.以上三式分别相加得到:2(PA+PB+PC)>AB+BC+AC,即PA+PB+PC>(AB+BC+AC).考点二:8字模型【例2】.如图,∠1=60°,则∠A+∠B+∠C+∠D+∠E+∠F=解:由三角形外角的性质得:∠3=∠A+∠E,∠2=∠F+∠D,∵∠1+∠2+∠3=180°,∠1=60°,∴∠2+∠3=120°,即:∠A+∠E+∠F+∠D=120°,∵∠B+∠C=120°,∴∠A+∠B+∠C+∠D+∠E+∠F=240°.变式训练【变式2-1】.如图,∠A+∠B+∠C+∠D+∠E+∠F=360°.解:在△ACE中:∠A+∠C+∠E=180°,在△BDF中:∠B+∠D+∠F=180°,则:∠A+∠B+∠C+∠D+∠E+∠F=360°,故答案为:360.【变式2-2】.如图,A,B,C,D,E,F是平面上的6个点,则∠A+∠B+∠C+∠D+∠E+∠F 的度数是360度.解:延长FE交AB于M,设FE交CD于N,∵∠CNE=∠D+∠DEF,∠FMB=∠F+∠A,又∵∠C+∠B+∠CNE+∠FMB=360°,∴∠C+∠B+∠D+∠DEF+∠F+∠A=360°,即∠A+∠B+∠C+∠D+∠DEF+∠F=360°,故答案为:360.【变式2-3】.如图,∠A+∠B+∠C+∠D+∠E+∠F=360°.解:∵∠1=∠A+∠B,∠2=∠C+∠D,又∵∠1+∠2+∠E+∠F=360°∴∠A+∠B+∠C+∠D+∠E+∠F=360°.故答案为:360.实战演练【变式2-4】.一副三角板如图摆放,其中一块三角板的直角边EF 落在另一块三角板的斜边AC 上,边BC 与DF 交于点O ,则∠BOD 的度数是105°.解:△COF 中,∵∠CFO =45°,∠FCO =30°,∴∠COF =180°﹣∠CFO ﹣∠FCO =180°﹣45°﹣30°=105°,∵∠COF =∠BOD ,∴∠BOD=105°,故答案为:105°.1.如图,已知AB ⊥BD ,AC ⊥,∠A =35°,则∠D 的度数为()A .35°B .45°C .55°D .65°解:因为∠AEB 与∠DEC 是一组对顶角,所以∠AEB =∠DEC .在△ABO 中AB ⊥BD ,∠A =35°,所以∠AEB =65°.在△DCO 中AC ⊥CD ,∠DEC =65°,所以∠D =35°.故选:A .2.如图,∠A +∠B +∠C +∠D +∠E 的度数为()A.120°B.150°C.180°D.200°解:如图可知:∵∠4是三角形的外角,∴∠4=∠A+∠2,同理∠2也是三角形的外角,∴∠2=∠E+∠C,在△BDG中,∵∠B+∠D+∠4=180°,∴∠B+∠E+∠A+∠D+∠C=180°.故选:C.3.如图,在△ABC中,M,N分别是边AB,BC上的点,将△BMN沿MN折叠;使点B落在点B'处,若∠B=35°,∠BNM=28°,则∠AMB'的度数为()A.30°B.37°C.54°D.63°解:∵△BMN沿MN折叠,使点B落在点B'处,∴△BMN≌△B'MN,∴∠BMN=∠B'MN,∵∠B=35°,∠BNM=28°,∴∠BMN=180°﹣35°﹣28°=117°,∠AMN=35°+28°=63°,∴∠AMB'=∠B'MN﹣∠AMN=117°﹣63°=54°,故选:C.4.如图,将分别含有30°、45°角的一副三角板重叠,使直角顶点重合,若两直角重叠形成的角为65°,则图中角α的度数为140°.解:如图,∵∠B=30°,∠DCB=65°,∴∠DFB=∠B+∠DCB=30°+65°=95°,∴∠α=∠D+∠DFB=45°+95°=140°,故答案为:140°.5.已知如图,BQ平分∠ABP,CQ平分∠ACP,∠BAC=α,∠BPC=β,则∠BQC=(α+β).(用α,β表示)解:连接BC,∵BQ平分∠ABP,CQ平分∠ACP,∴∠3=ABP,∠4=ACP,∵∠1+∠2=180°﹣β,2(∠3+∠4)+(∠1+∠2)=180°﹣α,∴∠3+∠4=(β﹣α),∵∠BQC=180°﹣(∠1+∠2)﹣(∠3+∠4)=180°﹣(180°﹣β)﹣(β﹣α),即:∠BQC=(α+β).故答案为:(α+β).6.如图,则∠A+∠B+∠C+∠D+∠E+∠F+∠H=540度.解:如图,连接CH,由三角形的内角和定理得,∠A+∠B=∠1+∠2,由多边形的内角和公式得,∠1+∠2+∠C+∠D+∠E+∠F+∠H=(5﹣2)•180°=540°,所以,∠A+∠B+∠C+∠D+∠E+∠F+∠H=540°.故答案为:540.7.如图,求∠A+∠B+∠C+∠D+∠E+∠F=230°.解:∵∠1=∠A+∠B,∠2=∠D+∠E,又∵∠1+∠F=115°,∠2+∠C=115°,∴∠A+∠B+∠C+∠D+∠E+∠=115°+115°=230°.故答案为:230°.8.如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I+∠K的度数为解:连KF,GI,如图,∵7边形ABCDEFK的内角和=(7﹣2)×180°=900°,∴∠A+∠B+∠C+∠D+∠E+∠F+∠K=900°﹣(∠1+∠2),即∠A+∠B+∠C+∠D+∠E+∠F+∠K+(∠1+∠2)=900°,∵∠1+∠2=∠3+∠4,∠5+∠6+∠H=180°,∴∠A+∠B+∠C+∠D+∠E+∠F+∠K+(∠3+∠4)=900°,∴∠A+∠B+∠C+∠D+∠E+∠F+∠K+(∠3+∠4)+∠5+∠6+∠H=900°+180°,∴∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I+∠K=1080°.故选:C.9.如图是可调躺椅示意图(数据如图),AE与BD的交点为C,且∠A,∠B,∠E保持不变.为了舒适,需调整∠D的大小,使∠EFD=110°,则图中∠D应减少(填“增加”或“减少”)10度.解:连接CF,并延长至点M,如图所示.在△ABC中,∠A=50°,∠B=60°,∴∠ACB=180°﹣∠A﹣∠B=180°﹣50°﹣60°=70°,∴∠DCE=∠ACB=70°.∵∠DFM=∠DCF+∠D,∠EFM=∠ECF+∠E,∴∠EFD=∠DCF+∠ECF+∠D+∠E=∠DCE+∠D+∠E,即110°=70°+∠D+30°,∴∠D=10°,∴20°﹣10°=10°,∴图中∠D应减少(填“增加”或“减少”)10度.故答案为:减少;10.10.如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I的值.解:如图所示,分别延长BC、IH交EF于点M、N,由三角形的外角的性质可知:∠C+∠D=∠1,∠G+∠H=∠2,∠4=∠1+∠B=∠C+∠D+∠B,∠3=∠2+∠F=∠G+∠H+∠F,∴∠3+∠4=∠5+∠HNM+∠5+∠CMN=180°+∠5,∵∠5=∠6=360°﹣∠A﹣∠B﹣∠I,∴∠C+∠D+∠B+∠G+∠H+∠F=180°+360°﹣∠A﹣∠B﹣∠I,∴∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I=180°+360°=540°11.如图,已知AB∥DE,∠ABC、∠CED的平分线交于点F.探究∠BFE与∠BCE之间的数量关系,并证明你的结论.解:过点C作直线MN∥AB,∵AB∥DE,MN∥AB,∴MN∥DE,∴∠DEC=∠ECN,∵AB∥DE,∴∠ABC=∠BCN,∴∠BCE=∠ABC+∠DEC,同理∠BFE=∠ABF+∠DEF,∵∠ABC、∠CED的平分线交于点F,∴∠ABC=2∠ABF,∠DEC=2∠DEF,∴∠BCE=2∠ABF+2∠DEF=2∠BFE.12.如图,DP平分∠ADC,PB平分∠ABC,求证:∠P=(∠A+∠C)证明:如右图所示,∵∠CMP=∠C+∠CDP=∠P+∠CBP,∠ANP=∠P+∠ADP=∠A+∠ABP,∴∠P+∠CBP+∠P+∠ADP=∠C+∠CDP+∠A+∠ABP,又∵DP、BP是∠ADC、∠ABC的角平分线,∴∠CDP=∠ADP,∠CBP=∠ABP,∴2∠P=∠C+∠A,∴∠P=(∠A+∠C).13.如图,在四边形ABCD中,AM、CM分别平分∠DAB和∠DCB,AM与CM交于M.探究∠AMC与∠B、∠D间的数量关系.解:∠AMC=180°﹣∠B+∠D,理由如下:∵AM、CM分别平分∠DAB和∠DCB,∴∠BAD=2∠BAM,∠BCD=2∠BCM,∵∠BAD+∠B+∠BCD+∠d=360°,∴∠BAM+∠BCM+∠B+∠D=180°,∴∠BAM+∠BCM=180°﹣∠B﹣∠D,∵∠B+∠AMC+∠BAM+∠BCM=∠B+∠AMC+180°﹣∠B﹣∠D=360°,∴∠AMC=360°﹣(180°﹣∠B﹣∠D)﹣∠B=180°﹣∠B+∠D.14.(1)探究:如图1,求证:∠BOC=∠A+∠B+∠C.(2)应用:如图2,∠ABC=100°,∠DEF=130°,求∠A+∠C+∠D+∠F的度数.解:(1)作射线AO,∵∠3是△ABO的外角,∴∠1+∠B=∠3,①∵∠4是△AOC的外角,∴∠2+∠C=∠4,②①+②得,∠1+∠B+∠2+∠C=∠3+∠4,即∠BOC=∠A+∠B+∠C;(2)连接AD,同(1)可得,∠F+∠2+∠3=∠DEF③,∠1+∠4+∠C=∠ABC④,③+④得,∠F+∠2+∠3+∠1+∠4+∠C=∠DEF+∠ABC=130°+100°=230°,即∠BAF+∠C+∠CDE+∠F=230°.15.如图1,已知线段AB、CD相交于点O,连接AC、BD,我们把形如图1的图形称之为“8字形“.如图2,∠CAB和∠BDC的平分线AP和DP相交于点P,并且与CD、AB分别相交于点M、N.试解答下列问题:①仔细观察,在图2中有3个以线段AC为边的“8字形”;②若∠B=76°,∠C=80°,试求∠P的度数;③∠C和∠B为任意角时AP、DP分别是∠CAB、∠BDC的三等分线,写出∠P与∠C、∠B之间数量关系,并说明理由.解:①3;故答案为3.②证明:∵∠CAB和∠BDC的平分线AP和DP相交于点P,∴∠CAP=∠BAP,∠BDP=∠CDP,∵∠CAP+∠C=∠CDP+∠P,∠BAP+∠P=∠BDP+∠B,∴∠C﹣∠P=∠P﹣∠B,即∠P=(∠C+∠B),∵∠C=80°,∠B=76°,∴∠P=(80°+76°)=78°;③∠P=(2∠C+∠B)或∠P=(∠C+2∠B).证明:设∠CAB=3α,∠BDC=3β,i)如图3,∠CAP:∠BAP=∠CDP:∠BDP=2:1,∴∠CAP=2α,∠BAP=α,∠BDP=β,∠CDP=2β,∵∠CAP+∠C=∠CDP+∠P,∠BAP+∠P=∠BDP+∠B,∴∠C﹣∠P=2β﹣2α,∠P﹣∠B=β﹣α,∴∠C﹣∠P=2∠P﹣2∠B,∴∠P=(∠C+2∠B),ii)如图4,∠CAP:∠BAP=∠CDP:∠BDP=1:2,∴∠CAP=α,∠BAP=2α,∠BDP=2β,∠CDP=β,∵∠CAP+∠C=∠CDP+∠P,∠BAP+∠P=∠BDP+∠B,∴∠C﹣∠P=β﹣α,∠P﹣∠B=2β﹣2α,∴2(∠C﹣∠P)=∠P﹣∠B,∴∠P=(2∠C+∠B),16.阅读材料,回答下列问题:【材料提出】“八字型”是数学几何的常用模型,通常由一组对顶角所在的两个三角形构成.【探索研究】探索一:如图1,在八字型中,探索∠A、∠B、∠C、∠D之间的数量关系为∠A+∠B=∠C+∠D;探索二:如图2,若∠B=36°,∠D=14°,求∠P的度数为25°;探索三:如图3,CP、AG分别平分∠BCE、∠FAD,AG反向延长线交CP于点P,则∠P、∠B、∠D之间的数量关系为∠P=.【模型应用】应用一:如图4,延长BM、CN,交于点A,在四边形MNCB中,设∠M=α,∠N=β,α+β>180°,四边形的内角∠MBC与外角∠NCD的角平分线BP,CP相交于点P,则∠A=α+β﹣180°(用含有α和β的代数式表示),∠P=.(用含有α和β的代数式表示)应用二:如图5,在四边形MNCB中,设∠M=α,∠N=β,α+β<180°,四边形的内角∠MBC与外角∠NCD的角平分线所在的直线相交于点P,∠P=.(用含有α和β的代数式表示)【拓展延伸】拓展一:如图6,若设∠C=x,∠B=y,∠CAP=∠CAB,∠CDP=∠CDB,试问∠P与∠C、∠B之间的数量关系为∠P=.(用x、y表示∠P)拓展二:如图7,AP平分∠BAD,CP平分∠BCD的邻补角∠BCE,猜想∠P与∠B、∠D的关系,直接写出结论2∠P﹣∠B﹣∠D=180°.解:探索一:如图1,∵∠AOB+∠A+∠B=∠COD+∠C+∠D=180°,∠AOB=∠COD,∴∠A+∠B=∠C+∠D,故答案为∠A+∠B=∠C+∠D;探索二:如图2,∵AP、CP分别平分∠BAD、∠BCD,∴∠1=∠2,∠3=∠4,由(1)可得:∠1+∠B=∠3+∠P,∠2+∠P=∠4+∠D,∴∠B﹣∠P=∠P﹣∠D,即2∠P=∠B+∠D,∵∠B=36°,∠D=14°,∴∠P=25°,故答案为25°;探索三:由①∠D+2∠1=∠B+2∠3,由②2∠B+2∠3=2∠P+2∠1,①+②得:∠D+2∠B+2∠1+2∠3=∠B+2∠3+2∠P+2∠1∠D+2∠B=2∠P+∠B.∴∠P=.故答案为:∠P=.应用一:如图4,由题意知延长BM、CN,交于点A,∵∠M=α,∠N=β,α+β>180°,∴∠AMN=180°﹣α,∠ANM=180°﹣β,∴∠A=180°﹣(∠AMN+∠ANM)=180°﹣(180°﹣α+180°﹣β)=α+β﹣180°;∵BP、CP分别平分∠ABC、∠ACB,∴∠PBC=∠ABC,∠PCD=∠ACD,∵∠PCD=∠P+∠PBC,∴∠P=∠PCD﹣∠PBC=(∠ACD﹣∠ABC)=∠A=,故答案为:α+β﹣180°,;应用二:如图5,延长MB、NC,交于点A,设T是CB的延长线上一点,R是BC延长线上一点,∵∠M=α,∠N=β,α+β<180°,∴∠A=180°﹣α﹣β,∵BP平分∠MBC,CP平分∠NCR,∴BP平分∠ABT,CP平分∠ACB,由应用一得:∠P=∠A=,故答案为:;拓展一:如图6,由探索一可得:∠P+∠PAB=∠B+∠PDB,∠P+∠CDP=∠C+∠CAP,∠B+∠CDB=∠C+∠CAB,∵∠C=x,∠B=y,∠CAP=∠CAB,∠CDP=∠CDB,∴∠CDB﹣∠CAB=∠C﹣∠B=x﹣y,∠PAB=∠CAB,∠PDB=∠CDB,∴∠P+∠CAB=∠B+∠CDB,∠P+∠CDB=∠C+∠CAB,∴2∠P=∠C+∠B+(∠CDB﹣∠CAB)=x+y+(x﹣y)=,∴∠P=,故答案为:∠P=;拓展二:如图7,∵AP平分∠BAD,CP平分∠BCD的邻补角∠BCE,∴∠PAD=∠BAD,∠PCD=90°+∠BCD,由探索一得:①∠B+∠BAD=∠D+∠BCD,②∠P+∠PAD=∠D+∠PCD,②×2,得:③2∠P+∠BAD=2∠D+180°+∠BCD,③﹣①,得:2∠P﹣∠B=∠D+180°,∴2∠P﹣∠B﹣∠D=180°,故答案为:2∠P﹣∠B﹣∠D=180°.。
安全学原理讲义(PPT 37页)

安全社会类:安全管理工程、安全经济工程、安全法学 社会科学性的安全因素,指人与人、人与物,或物与物的
时间、空间和能量联系因素。 安全系统类:安全运筹技术、安全信息技术理论
系统科学性的安全信息与能量的整体联系因素。 安全人体类:安全生理学、安全心理学
工业活动中发生的重大火灾、爆炸或毒物泄漏事故, 并人身伤亡,财物严重受,环境严重污染的事故。
2002年11月1日起实施的《中华人民共和国安全生产法》 中界定:特别重大事故;重大事故;较大事故;一般事故
5)重大危险源: 生产、加工、搬运与使用或存储危险物质,其数量
大于或等于国家规定的危险物质的单元或设施。
究范畴和学科体系,掌握安全科学的基本原理和 方法,为后叙的专业课程奠定基础。
本课程的主要学习内容及方法
➢ 重要意义:
通过学习该门课程后,懂得保护人身健康、保护 国家财产、保护环境、加强理论与安全新技术的研究。
➢ 学习要求:
✓ 理解并熟悉安全科学、安全观、安全认识论、安全方法论、 安全生理及心理、安全社会原理、安全经济原理等内容的 基本概念和基本原理,掌握其实质;
✓ 例如:2005年1月17日国家安全生产监督管理局发布的数据显 示,2004年我国煤矿事故死亡6027人,其中有两起一次 死亡百人以上的特别重大事故。
✓ 2003年2月1日,美国“哥伦比亚”号航天飞机在20年内第 28次飞行返程途中失事,7名宇航员全部丧生。
➢ 这种安全状态与现代化生产不适应的严重情况, 迫使从事安全工作的专家、学者和管理人员探 索事故或灾害孕育、发生、发展的规律,去寻 求一种对事物的安全性可以进行本质的定性与 定量描述,能够对事故发生的可能性进行预测 的新的安全科学方法。安全科学正是在这种新 形势下应运而生的一门新兴的交叉学科。
2025版高考语文一轮复习讲义:学案37 《过秦论》《五代史伶官传序》

板块五2025版高考语文一轮复习讲义学案37《过秦论》《五代史伶官传序》复习任务1.梳理并积累两文中的文言基础知识,重点掌握古今异义词、多义实词“遂”“一”“振”“将”。
2.翻译重点句子,背诵课文。
活动一基础梳理1.通假字请指出下列句中的通假字,并解释意思。
①赢粮而景从“____”同“____”,___________②非及乡时之士也“____”同“____”,_____景像影子一样乡向先前影2.古今异义请写出下列加颜色词语的古义。
①宽厚而爱人古义:_________今义:丈夫或妻子,恋爱中男女的一方②才能不及中人古义:_________今义:为双方介绍买卖、调解纠纷等并做见证的人爱护别人平常的人③岂非人事哉古义:_________今义:人的离合、境遇、存亡等情况;关于工作人员的录用、培养、调配、奖惩等工作④则遣从事以一少牢告庙古义:_______________________今义:做,投身到(事业中去);(按某种办法)处理⑤其意气之盛古义:______今义:意志和气概,志趣和性格,由于主观和偏激而产生的情绪人的作为官名,这里泛指一般属官气势⑥盛以锦囊,负而前驱向前奔驰古义:__________今义:在前面起引导作用的人或事物3.多义实词请解释下列加颜色词的意思。
(1)遂①山东豪俊遂并起而亡秦族矣:__________②言既遂矣,至于暴矣(《诗经·氓》):___________________________③遂而鸡豚(《种树郭橐驼传》):__________④寻向所志,遂迷不复得路(《桃花源记》):___________于是,就成功,顺利地完成,称心如意成,养好终于,竟然(2)一①合从缔交,相与为一:______②六王毕,四海一(《阿房宫赋》):_____③固知一死生为虚诞,齐彭殇为妄作(《兰亭集序》):_______________④而或长烟一空,皓月千里(《岳阳楼记》):____⑤能不龟手一也(《五石之瓠》):___________⑥用心一也(《劝学》):_____一体统一把……看作一样全相同,一样专一(3)振①振长策而御宇内:______②新浴者必振衣(《屈原列传》):_____③振之以威怒(《谏太宗十思疏》):_______________④遂相腾击,振奋作声(《促织》):____________⑤如有地动,尊则振龙(《张衡传》):同“震”,震动⑥大命将泛,莫之振救(《论积贮疏》):同“赈”,救济举起抖动同“震”,威吓奋起,振作(4)将①率疲弊之卒,将数百之众:______②若不阙秦,将焉取之(《烛之武退秦师》):_____③果品酒馔只顾将来(《林教头风雪山神庙》):________④将子无怒,秋以为期(《诗经·氓》):_______⑤将信将疑:________率领将要拿,持愿,请且,又4.词类活用掌握下列加颜色词的活用类型,并解释意思。
冠心病健康教育讲义培训课件

• 冠心病是冠状动脉粥样硬化性心脏病的简 称。冠心病是动脉粥样硬化导致器官病变 的最常见类型,也是危害中老年人健康的 常见病。本病的发生与冠状动脉粥样硬化 狭窄的程度和支数有密切关系,也有一些 老年人冠状动脉粥样硬化性狭窄虽较严重, 并不一定都有胸痛、心悸等冠心病临床表 现。
冠心病健康教育讲义
• 5.冠心病具有家族遗传性,若家族中有人患上冠 心病,就更容易有心脏病发作。
冠心病健康教育讲义
9
哪些人易患冠心病
• 6.体重超重,患冠心病的可能性就比体重正常的 人要大。体重超重多过20%的人心脏病发作的可 能性比体重健康的人高三倍。
• 7.如果是从事经常坐着不动的工作,罹患冠状动 脉病的可能性就比从事包括体力劳动在内的工作 者要大。缺少运动心脏不强壮者得心脏病发作的 机会比健康者高出两倍。
• 3.将你习惯食用的肉类量减少 将你食用的 肉上脂肪除去 吃烧煮的肉 不要吃油煎的肉 每周最多只吃三只鸡蛋
• 4.吃大量水果及蔬菜 但饮食要维持平衡均 匀
• 5.减少盐的摄食量 摄食盐量低可以降低血 压并且减少发展冠状动脉病的危险。
冠心病健康教育讲义
34
• 6.经常运动 每周做两 三次剧烈运动 可减少 得心脏疾病的危险 但由于突然做剧烈运动 很危险 必须以渐进的方式来开始实行你的 运动计划
冠心病健康教育讲义
22
怎样早期发现冠心病?
• 冠心病是中老年人的常见病和多发病,处于这个 年龄阶段的人,在日常生活中,如果出现下列情 况,要及时就医,尽早发现冠心病。
• 1.劳累或精神紧张时出现胸骨后或心前区闷痛, 或紧缩样疼痛,并向左肩、左上臂放射,持续35分钟,休息后自行缓解者。
• 2.体力活动时出现胸闷、心悸、气短,休息时自 行缓解者。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三十七单元痰饮
细目一:概述
一、痰饮的概念及源流
1.痰饮的概念
痰饮是指体内水液输布、运化失常,停积于某些部位的一类病证。
2.痰饮的源流
《内经》无“痰”之证,而有“饮”、“饮积”之说,认为脾肾功能失调,湿邪淫溢,可发生停饮之病。
《金匮要略》始有痰饮名称,立专篇论述,并有广义、狭义之分。
该篇提出“用温药和之”的治疗原则,至今仍为临床遵循。
隋唐至金元,有痰证、饮证之分,逐渐发展了痰的病理学说,提出“百病兼痰”的论点。
《仁斋直指方》首先将饮与痰的概念作了明确的区分,提出饮清稀而痰稠浊。
叶天士总结前人治疗痰饮病的经验,重视脾、肾,提出了“外饮治脾,内饮治肾”的大法。
二、痰饮的分类
痰饮有广义、狭义之分。
广义痰饮包括痰饮、悬饮、溢饮、支饮四类,是诸饮的总称。
其中狭义的痰饮,则是指饮停胃肠之证。
三、痰饮与西医病名的关系
痰饮的临床表现多端,大致与西医学中的慢性支气管炎、支气管哮喘、渗出性胸膜炎、慢性胃炎、心力衰竭、肾炎水肿等有较密切联系。
细目二:病因病机
一、痰饮的常见病因
内因:饮食不当(暴饮过量、恣饮冷水、进食生冷),劳欲所伤。
外因:外感寒湿。
二、痰饮的基本病机及病机转化
痰饮的病位在三焦、肺、脾、肾,三脏之中,脾运失司,首当其冲。
基本病机为三焦失通失宣,肺失通调,脾失转输,肾失蒸化,阳虚水液不运,水饮停积为患。
病理性质总属阳虚阴盛,输化失调,因虚致实,水饮停积为患。
间有因时邪与里水相搏,或饮邪久郁化热,表现饮热相杂之候。
细目三:诊断和类证鉴别
一、各类痰饮的诊断要点
1.痰饮:心下满闷,呕吐清水痰涎,胃肠沥沥有声,形体昔肥今瘦,属饮停胃肠。
2.悬饮:胸胁饱满,咳唾引痛,喘促不能平卧,或有肺痨病史。
属饮流胁下。
3.溢饮:身体疼痛而沉重,甚则肢体浮肿,当汗出而不汗出或伴咳喘,属饮溢肢体。
4.支饮:咳逆倚息,短气不得平卧,其形如肿,属饮邪支撑胸肺。
二、痰、饮、水、湿的鉴别
痰多厚浊,无处不到,病变多端,属阳邪,多因热煎熬而成;
饮呈稀涎,多停于体内局部,属阴邪,多由寒积聚而生;
水为清液,每泛溢体表、全身,为阴类,但有阴阳之分;
湿黏而滞,发病缓慢,缠绵难解,属阴邪,每与他邪相兼为患。
细目四:辨证论治
一、痰饮、悬饮、支饮和溢饮的辨证要点
1.辨标本的主次:本虚为阳气不足,标实指水饮留聚。
2.辨病邪的兼夹:痰饮虽为阴邪,寒证居多,但亦有郁久化热者,初起若有寒热见证,为夹表邪;饮积不化,气机升降受阻,常兼气滞。
二、本病总的治疗原则
痰饮的治疗以温化为原则。
因饮为阴邪,遇寒则聚,得温则行。
通过温阳化气,可杜绝水饮之生成。
《金匮要略》提出:“病痰饮者,当以温药和之。
”同时还当根据表里虚实的不同,进行相应的处理。
水饮壅盛者,应祛饮以治标;阳微气衰者,宜温阳以治本;在表者,当温散发汗;在里者,应温化利水;正虚者补之,邪实者攻之,如属邪实正虚,则当消补兼施,饮热相杂者又当温清并用。
三、痰饮、悬饮、溢饮、支饮等证候的主症、治法和方药
【须牢记的架构图】
(一)痰饮
1.脾阳虚弱证
主症:胸胁支满,心下痞闷,胃中有振水音,脘腹喜温畏冷,泛吐清水痰涎,饮入易吐,口渴不欲饮水,头晕目眩,心悸气短,食少,大便或溏,形体逐渐消瘦,舌苔白滑,脉弦细而滑。
治法:温脾化饮。
代表方:苓桂术甘汤合小半夏加茯苓汤加减。
常用药:桂枝、甘草、白术、茯苓、半夏、生姜。
2.饮留胃肠证
主症:心下坚满或痛,自利,利后反快,虽利心下续坚满;或水走肠间,沥沥有声
舌干燥,舌苔腻、色白或黄,脉沉弦或伏。
治法:攻下逐饮。
代表方:甘遂半夏汤或己椒苈黄丸加减。
常用药:甘遂、半夏、白芍、蜂蜜、大黄、葶苈子、防己、椒目、甘草。
(二)悬饮
1.邪犯胸肺证
主症:寒热往来,身热起伏,汗少,或发热不恶寒,有汗而热不解,咳嗽,痰少,气急,胸胁刺痛,呼吸、转侧疼痛加重,心下痞硬,干呕,口苦,咽干,舌苔薄白或黄,脉弦数。
治法:和解宣利。
代表方:柴枳半夏汤加减。
常用药:柴胡、黄芩、瓜萎、半夏、枳壳、青皮、赤芍、桔梗、杏仁。
2.饮停胸胁证
主症:胸胁疼痛,咳唾引痛,痛势较前减轻,而呼吸困难加重,咳逆气喘,息促不能平卧,或仅能偏卧于停饮的一侧,病侧肋间胀满,甚则可见偏侧胸廓隆起,舌苔白,脉沉弦或弦滑。
治法:泻肺祛饮。
代表方:椒目瓜蒌汤合十枣汤加减或用控涎丹。
常用药:葶苈子、桑白皮、苏子、瓜萎皮、杏仁、枳壳、川椒目、茯苓、猪苓、泽泻、冬瓜皮、车前子、甘遂、大戟、芫花。
3.络气不和证
主症:胸胁疼痛,如灼如刺,胸闷不舒,呼吸不畅,或有闷咳,甚则迁延经久不已,阴雨天更甚,可见病侧胸廓变形,舌苔薄,质黯,脉弦。
治法:理气和络。
代表方:香附旋覆花汤加减。
常用药:旋覆花、苏子、柴胡、香附、枳壳、郁金、延胡索、当归须、赤芍、沉香。
4.阴虚内热证
主症:咳呛时作,咯吐少量黏痰,口干咽燥,或午后潮热,颧红,心烦,手足心热,盗汗,或伴胸胁闷痛,病久不复,形体消瘦,舌质偏红,少苔,脉小数。
治法:滋阴清热。
代表方:沙参麦冬汤合泻白散加减。
常用药:沙参、麦冬、玉竹、白芍、天花粉、桑白皮、桑叶、地骨皮、甘草。
(三)溢饮
表寒里饮证
主症:体沉身重而疼痛,甚则肢体浮肿,恶寒,无汗,或有咳喘,痰多白沫,胸闷,干呕,口不渴,苔白,脉弦紧。
治法:发表化饮。
代表方:小青龙汤加减。
常用药:麻黄、桂枝、半夏、干姜、细辛、五味子、白芍、炙甘草。
(四)支饮
1.寒饮伏肺证
主症:咳逆喘满不得卧,痰吐白沫量多,经久不愈,天冷受寒加重,甚至引起面浮跗肿。
或平素伏而不作,遇寒即发,发则寒热、背痛、腰疼、目泣自出、身体振振稠动。
舌苔白滑或白腻,脉弦紧。
治法:宣肺化饮。
代表方:小青龙汤加减。
常用药:麻黄、桂枝、干姜、细辛、半夏、厚朴、苏子、杏仁、甘草、五味子。
2.脾肾阳虚证
主症:喘促动则为甚,心悸,气短,或咳而气怯,痰多,食少,胸闷,怯寒肢冷,神疲,少腹拘急不仁,脐下动悸,小便不利,足跗浮肿,或吐涎沫而头目昏眩,舌体胖大,质淡,苔白润或腻,脉沉细而滑。
治法:温脾补肾,以化水饮。
代表方:金匮肾气丸合苓桂术甘汤加减。
常用药:桂枝、附子、黄芪、淮山药、白术、炙甘草、苏子、干姜、款冬花、钟乳石、沉香、补骨脂、山萸肉。
四、悬饮等常见证候治疗的加减变化
悬饮邪犯胸肺,痰饮内结,肺气失肃,加白苍子、桑白皮;心下痞硬,口苦,干呕加黄连;身热盛汗出,咳嗽气粗,去柴胡,加麻黄、杏仁、石膏。
饮停胸胁,痰浊偏盛,加薤白、杏仁;水饮久停难去,加桂枝、白术、甘草等。
络气不和,痰气郁阻,加瓜蒌、枳壳;久痛入络,痛势如刺者,加桃仁、红花、乳香、没药;饮留不净者,加通草、路路通、冬瓜皮等以祛饮通络。
阴虚内热,潮热显著,加鳖甲、功劳叶;虚热灼津为痰,肺失宣肃,加百部、川贝母;痰阻气滞,络脉失畅,加瓜萎皮、枳壳、广郁金、丝瓜络;日久积液未尽,加牡蛎、泽泻利水化饮;兼有神疲、气短、易汗、面色白者,酌加太子参、黄芪、五味子益气敛液。
本证须防迁延日久,趋向劳损之途。
