09组合变形习题
材料力学组合变形习题

材料力学组合变形习题L1AL101ADB (3)偏心压缩时,截面的中性轴与外力作用点位于截面形心的两侧,则外力作用点 到形心之距离e和中性轴到形心距离d之间的关系有四种答案:(A ) e=d; (B ) e>d;(C ) e越小,d越大; (D ) e越大,d越小。
正确答案是______。
答案(C )1BL102ADB (3)三种受压杆件如图。
设杆1、杆2和杆3中的最大压应力(绝对值)分别用 max1σ、max 2σ和max3σ表示,现有下列四种答案:(A )max1σ=max 2σ=max3σ; (B )max1σ>max 2σ=max3σ;(C )max 2σ>max1σ=max3σ; (D )max 2σ<max1σ=max3σ。
正确答案是______。
答案(C )1BL103ADD (1)在图示杆件中,最大压应力发生在截面上的哪一点,现有四种答案:(A )A点; (B )B点; (C )C点; (D )D点。
正确答案是______。
答案(C )1AL104ADC (2)一空心立柱,横截面外边界为正方形, 内边界为等边三角形(二图形形心重 合)。
当立柱受沿图示a-a线的压力时,此立柱变形形态有四种答案:(A )斜弯曲与中心压缩组合; (B )平面弯曲与中心压缩组合;(C )斜弯曲; (D )平面弯曲。
正确答案是______。
答案(B )1BL105ADC (2)铸铁构件受力如图所示,其危险点的位置有四种答案:(A )①点; (B )②点; (C )③点; (D )④点。
正确答案是______。
答案(D )1BL106ADC (2)图示矩形截面拉杆中间开一深度为h/2的缺口,与不开口的拉杆相比,开口处的最大应力的增大倍数有四种答案:(A )2倍; (B )4倍; (C )8倍; (D )16倍。
正确答案是______。
答案(C )1BL107ADB (3)三种受压杆件如图,设杆1、杆2和杆3中的最大压应力(绝对值)分别用 max1σ、max 2σ和max3σ表示,它们之间的关系有四种答案:(A )max1σ<max 2σ<max3σ; (B )max1σ<max 2σ=max3σ;(C )max1σ<max3σ<max 2σ; (D )max1σ=max3σ<max 2σ。
工程力学习题集(二)
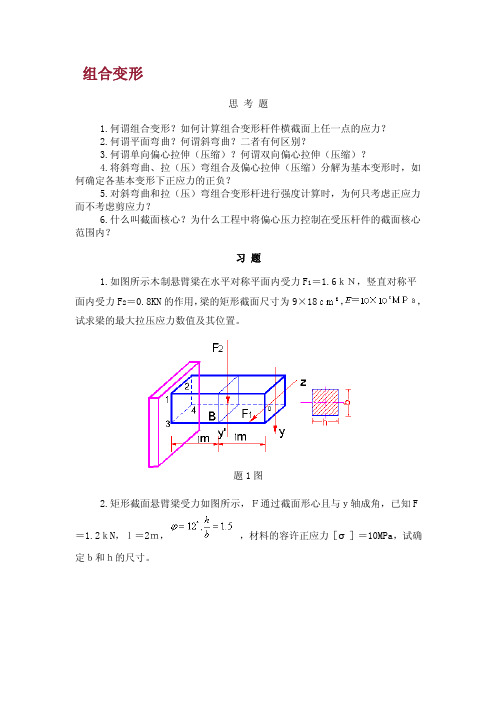
组合变形思考题1.何谓组合变形?如何计算组合变形杆件横截面上任一点的应力?2.何谓平面弯曲?何谓斜弯曲?二者有何区别?3.何谓单向偏心拉伸(压缩)?何谓双向偏心拉伸(压缩)?4.将斜弯曲、拉(压)弯组合及偏心拉伸(压缩)分解为基本变形时,如何确定各基本变形下正应力的正负?5.对斜弯曲和拉(压)弯组合变形杆进行强度计算时,为何只考虑正应力而不考虑剪应力?6.什么叫截面核心?为什么工程中将偏心压力控制在受压杆件的截面核心范围内?习题1.如图所示木制悬臂梁在水平对称平面内受力F1=1.6kN,竖直对称平面内受力F2=0.8KN的作用,梁的矩形截面尺寸为9×18,,试求梁的最大拉压应力数值及其位置。
题1图2.矩形截面悬臂梁受力如图所示,F通过截面形心且与y轴成角,已知F =1.2kN,l=2m,,材料的容许正应力[σ]=10MPa,试确定b和h的尺寸。
题2图3.承受均布荷载作用的矩形截面简支梁如图所示,q与y轴成角且通过形心,已知l=4m,b=10cm,h=15cm,材料的容许应力[σ]=10MPa,试求梁能承受的最大分布荷载。
题3图4.如图所示斜梁横截面为正方形,a=10cm,F=3kN作用在梁纵向对称平面内且为铅垂方向,试求斜梁最大拉压应力大小及其位置。
题4图5.柱截面为正方形,边长为a,顶端受轴向压力F作用,在右侧中部挖一个槽(如图),槽深。
求开槽前后柱内的最大压应力值。
题5图6.砖墙及其基础截面如图,设在1m长的墙上有偏心力F=40kN的作用,试求截面1-1和2-2上的应力分布图。
题6图7.矩形截面偏心受拉木杆,偏心力F=160kN,e=5cm,[σ]=10MPa,矩形截面宽度b=16cm,试确定木杆的截面高度h。
题7图8.一混凝土重力坝,坝高H=30m,底宽B=19m,受水压力和自重作用。
已知坝前水深H=30m,坝体材料容重,许用应力[]=10MPa,坝体底面不允许出现拉应力,试校核该截面正应力强度。
材料力学习题组合变形#(精选.)

组合变形基 本 概 念 题一、选择题1. 偏心压缩时,截面的中性轴与外力作用点位于截面形心的两侧,则外力作用点到 形心的距离e 和中性轴到形心距离d 之间的关系是( )。
A .e = dB .e >dC .e 越小,d 越大D .e 越大,d 越小2.三种受压杆件如图所示,设杆1、杆2和杆3中的最大压应力(绝对值)分别用1max σ、2max σ、3max σ表示,则( )。
A .1max σ=2max σ=3max σB .1max σ>2max σ=3max σC .2max σ>1max σ=3max σD .2max σ<1max σ=3max σ 题2图3.在图示杆件中,最大压应力发生在截面上的( )。
A .A 点B .B 点C .C 点D .D 点题3图 题4图4. 铸铁杆件受力如图4所示,危险点的位置是( )。
A .①点B .②点C .⑧点D .④点5. 图示正方形截面直柱,受纵向力P 的压缩作用。
则当P 力作用点由A 点移至B 点时柱内最大压应力的比值()max A σ﹕()max B σ为( )。
A .1﹕2B .2﹕5C .4﹕7D .5﹕26. 图示矩形截面偏心受压杆件发生的变形为( )。
A .轴向压缩和平面弯曲组合B .轴向压缩,平面弯曲和扭转组合C .轴向压缩,斜弯曲和扭转组合D .轴向压缩和斜弯曲组合-41-题5图 题6图 7. 图所示悬臂梁的横截面为等边角钢,外力P 垂直于梁轴,其作用线与形心轴y 垂直,那么该梁所发生的变形是( )。
A .平面弯曲B .扭转和斜弯曲C .斜弯曲D .两个相互垂直平面(xoy 平面和xoz 平面)内的平面弯曲题7图 8. 图示正方形截面杆受弯扭组合变形,在进行强度计算时,其任一截面的危险点位置有四种答案,正确的是( )。
A .截面形心B .竖边中点A 点C .横边中点B 点D .横截面的角点D 点题8图 题9图9. 图示正方形截面钢杆,受弯扭组合作用,若已知危险截面上弯矩为M ,扭矩为T ,截面上A 点具有最大弯曲正应力σ和最大剪应力τ,其抗弯截面模量为W 。
工程力学之组 合 变 形

工程力学第10章组合变形学习目标(1)了解组合变形的概念及其强度问题的分析方法;(2)掌握斜弯曲、拉伸(压缩)与弯曲和偏心压缩的应力及强度计算。
10.1 组合变形的概念例如,烟囱的变形,除自重W引起的轴向压缩外,还有水平风力引起的弯曲变形,同时产生两种基本变形,如图10-1(a)所示。
又如图10-1(b)所示,设有吊车的厂房柱子,作用在柱子牛腿上的荷载F,它们合力的作用线偏离柱子轴线,平移到轴线后同时附加力偶。
此时,柱子既产生压缩变形又产生弯曲变形。
再如图10-1(c)所示的曲拐轴,在力F作用下,AB 段同时产生弯曲变形和扭转变形。
10.1 组合变形的概念图10-110.1 组合变形的概念上述这些构件的变形,都是两种或两种以上的基本变形的组合,称为组合变形。
研究组合变形问题依据的是叠加原理,进行强度计算的步骤如下:(1)将所作用的荷载分解或简化为几个只引起一种基本变形的荷载分量。
(2)分别计算各个荷载分量所引起的应力。
(3)根据叠加原理,将所求得的应力相应叠加,即得到原来荷载共同作用下构件所产生的应力。
(4)判断危险点的位置,建立强度条件。
10.2例如图10-2(a)所示的横截面为矩形的悬臂梁,外力F作用在梁的对称平面内,此类弯曲称为平面弯曲。
斜弯曲与平面弯曲不同,如图10-2(b)所示同样的矩形截面梁,外力F的作用线通过横截面的形心而不与截面的对称轴重合,此梁弯曲后的挠曲线不再位于梁的纵向对称面内,这类弯曲称为斜弯曲。
斜弯曲是两个平面弯曲的组合,本节将讨论斜弯曲时的正应力及其强度计算。
10.2图10-210.210.2.1 正应力计算斜弯曲时,梁的横截面上同时存在正应力和切应力,但因切应力值很小,一般不予考虑。
下面结合图10-3(a)所示的矩形截面梁说明斜弯曲时正应力的计算方法。
图10-310.2.1 正应力计算10.2.1.1 外力的分解由图10-3(a)可知:10.2.1.2 内力的计算如图10-3(b)所示,距右端为a 的横截面上由F y 、F z 引起的弯曲矩分别是:10.2 10.2.1 正应力计算10.2.1.3 应力的计算由M z 和M y (即F y 和F z )在该截面引起K 点的正应力分别为:F y 和F z 共同作用下K 点的正应力为:10.210-110.210.2.1 正应力计算10.2.1.3 应力的计算通过以上分析过程,我们可以将组合变形问题计算的思路归纳为“先分后合”,具体如下:10.210.2.2 正应力强度条件同平面弯曲一样,斜弯曲梁的正应力强度条件仍为:10-2即危险截面上危险点的最大正应力不能超过材料的许用应力[σ]。
材料力学_陈振中_习题第九章组合变形
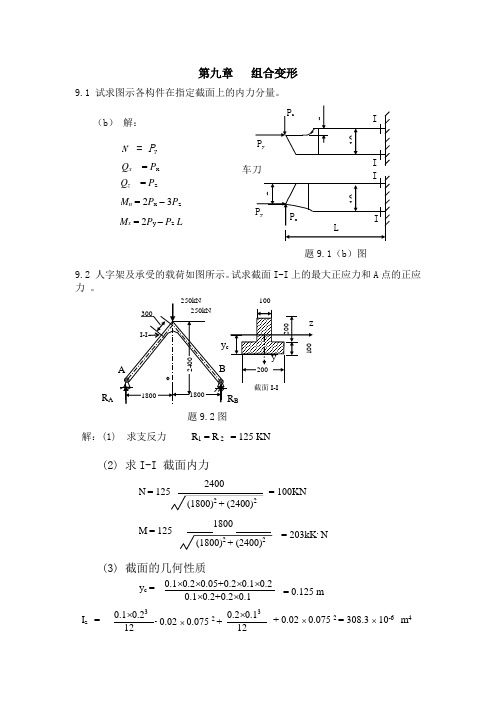
第九章组合变形9.1 试求图示各构件在指定截面上的内力分量。
9.2 人字架及承受的载荷如图所示。
试求截面I-I上的最大正应力和A点的正应力9.3 图示起重架的最大起吊重量(包括行走小车等)为P = 40kN ,横梁AC 由两根No.18槽钢组成,材料为A3钢,许用应力[σ] = 120 MPa 。
试校核横梁的强度。
9.7 图示短柱受载荷P 和H 的作用,试求固定端截面上角点A 、B 、C 及D 的正应力,并确定其中性轴的位置。
9.14 图为操纵装置水平杆,截面为空心圆形,内径d = 24 mm,外径D = 30 mm。
材料为A3钢,[σ] = 100 MPa。
控制片受力P1= 600 N。
试用第三强度理论校核杆的强度。
9.17图示皮带轮传动轴,传递功率N = 7kW,转速n =200r/min。
皮带轮重量Q = 1.8kN。
左端齿轮上啮合力Pn与齿轮节圆切线的夹角(压力角)为200。
轴的材料为A5钢,其许用应力[σ] = 80 MPa。
试分别在忽略和考虑皮带轮重量的两种情况下,按第三强度理论估算轴的直径。
9.19 飞机起落架的折轴为管状截面,内径d =70 mm ,外径D = 80 mm 。
材料的许用应力[σ] = 100 MPa ,试按第三强度理论校核折轴的强度。
若P = 1 kN ,Q = 4 kN 。
9.24 端截面密封的曲管的外径为100mm ,壁厚t = 5mm ,内压p = 8MPa 。
集中力P = 3kN 。
A 、B 两点在管的外表面上,一为截面垂直直径的端点,一为水平直径的端点。
试确定两点的应力状态。
解:在内压p 作用下,B 点应力状态分别如图9.24a ,b 所示。
σp1 = pD/(2t) = 8⨯100/(2⨯5) = 80 MPa, σp2 = pD/(4t) = 40 MPa 在集中力P 作用下,曲管受弯扭组合变形,A 点和B 点应力状态分别如图9.24c ,d 所示。
材料力学第八章组合变形

例题: 图示吊车大梁,由32a热轧普通工字钢制成,许 用应力 [σ]=160MPa ,L=4m 。起吊的重物重量F =80kN,且作用在梁的中点,作用线与y轴之间的夹角α =5°,试校核吊车大梁的强度是否安全。
F
Fy F cos 50
L2
L2
解:1. 外力分解
Fy F cos 80 cos 50 79.7kN Fz F sin 80 sin 50 6.96kN
材料力学
Mechanics of Materials
例:图示梁,已知F1=800N,F2=1650N,截面宽度 b=90mm,高度h=180mm。求:
1、梁上的max及所在位置; 2、若改为a=130mm的正方形截面,梁上的max; 3、若改为d=130mm圆形截面,梁上的max。
F2
F1 z
32
32 6
d3
72.6mm
取 d 73mm
构件在荷载的作用 下如发生两种或两种以 上基本形式的变形,且 几种变形所对应的应力 (和变形)属于同一数 量级,则构件的变形称 为组合变形。
❖组合变形的分析方法 线弹性小变形范围内,采用叠加原理
材料力学
Mechanics of Materials
二.组合变形分析方法 条件:线弹性小变形
组合 变形
0.642q 106 31.5 103
0.266q 106 237 103
160MPa
q 7.44kN / m
材料力学
Mechanics of Materials
M zD 0.456q
M zA 0.266q
z
M yD 0.444q
M yA 0.642q
A截面
y
max
材料力学 第11章 组合变形习题集

横截面m-m上任一点C(y,z)处由 弯矩Mz和My引起的正应力分别为
M z y M cos y M y z M sin z
Iz
Iz
Iy
Iy
38
C点的正应力
' ''
M
cos
Iz
y
sin
Iy
z
悬臂梁固定端截面A的弯矩Mz和My 均达到最大值,故该截
面是危险截面。设yo、zo为中性轴上任一点的坐标,并令σ
算 圆轴表面上与轴线成30°方位上的正应变。
32
解: (1)由内力图知,所有截面均为危险截面,危险点为靠近
轴表面的各点,应力状态如图。计算危险点的主应力。轴力
引起的正应力
FN 4F
A πd 2
扭矩引起的切应力
T M 8F
Wp Wp 5πd 2
危险点处的主应力为
1
2
(
)2
( )2
它在y、z两轴上的截距分别为
y* z* h / 2
该截面惯性半径的平方为
iy2
Iy A
h2 12
iz2
Iz A
b2 12
28
中性轴①对应的核心边界上点1的坐标为
ey1
iz2 y*
0
ez1
iy2 z*
h 6
按上述方法可求得与它们对应的截面核
心边界上的点2、3、4,其坐标依次为:
ey2
b 6
ez2 0
车臂的直径d。
18
解:两个缆车臂各承担缆车重量的一半,如 图。则缆车臂竖直段轴力为FN=W/2=3kN 弯矩为M=Wb/2=540N·m 危险截面发生在缆车臂竖直段左侧,由强度条件
结构力学 第八章
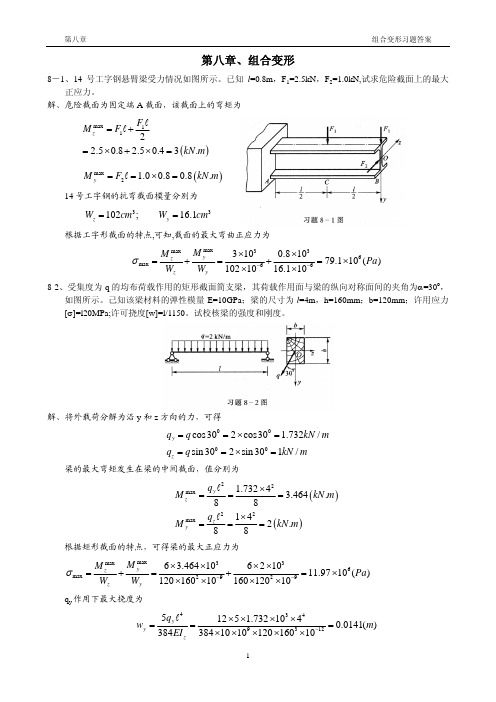
wmax 0.0202 0.76 1 = = < l 4 150 150
解、将均布载荷分解为沿轴线方向和垂直于轴线方向的两个分力,可得: qx = q sin α ; 距离 B 端为 x 的截面上的轴力和弯矩分别为
q y = q cos α
M=
该截面的最大压应力为
q y lx 2
−
qy x2 2
=
q ( lx − x 2 ) cos α 2
σ
所以该点最大切应力为: τ max =
8-16、铁道路标圆信号板,装在外径 D=60mm 的空心圆柱上,所受的最大风载 p=2kN/m2,[σ]=60MPa。试 按第三强度理论选定空心柱的厚度。
解、结构的危险截面为空心柱的固定端,截面的弯矩和扭矩分别为
M = 2×
π × 0.52
4
× 0.8 = 0.314(kN .m);
当中性轴为①时,中性轴的截矩为: 偏心力作用点的位置为:
a y = −0.3; az → ∞ ;
z
②
iz2 0.019333 ey = − = − = 0.0644(m), ay −0.3
当中性轴为②时,中性轴的截矩为: 偏心力作用点的位置为:
iz2 ez = − = 0 az
①
a y = 0.4; az = −0.4 ;
解、将外载荷分解为沿 y 和 z 方向的力,可得
q y = q cos 300 = 2 × cos 300 = 1.732kN / m qz = q sin 300 = 2 × sin 300 = 1kN / m
梁的最大弯矩发生在梁的中间截面,值分别为
M zmax =
max My
1.732 × 42 = 3.464 ( kN .m ) 8 8 q z l 2 1× 4 2 = = = 2 ( kN .m ) 8 8 =
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图示矩形截面拉杆中间开一深度为h/2的缺口,与不开口的拉杆相比,开中处的最大应力的增大倍数有四种答案:
(A) 2倍;(B) 4倍;(C) 8倍;(D) 16倍;
正确答案是_________________。
04.三种受压杆件如图,设杆1、2、和杆3中的最大压应力(绝对值)分别用 、 和 表示,它们之间的关系有四种答案:
18.试作用图示空间折杆的内力图,(弯曲剪应力图可略)。
19.矩形截面木受力如图,已知 , , ,试验算木条的强度和刚度。
20.图示矩形截面简支梁受均布载荷作用,载荷作用方向如图示, ,简支梁受均布载荷时平面弯曲的跨度挠度值 ,试求该梁的最大总挠度及挠曲线平面的位置。
21.悬重物架,如图所示。已知载荷 。
08用第三强度理论校核图示杆的强度时,有四种答案:
(A) ;
(B) ;
(C) ;
(D) ;
正确答案是__________________。
09.按第三强度理论计算等截面直杆弯扭组合变形的强度问题时,应采用的强度公式有四种答案:
(A) ;
(B) ;
(C) ;
(D) ;
正确答案是__________________。
06.图示正方形截面杆承受弯扭组合变形,在进行强度计算时,其任一截面的危险点位置有四种答案:
(A)截面形心;( B )竖边中点A点;( C )横边中点B点;( D )横截面的角点D点;
正确答案是__________________。
07.折杆危险截面上危险点的应力状态,现有四种答案:
正确答案是__________________。
第九章 组合变形部分
填空题
01.( 5 )偏心压缩实际不就是____________和____________的组合变形问题。
02.( 5 )铸铁构件受力如图所示,其危险点的位置有四中种答案:
( A )①点;( B )②点;( C )③点;( D )④点。
正确答案是_________________。
25.(20分)
图示一传动轴 许用应力 。试求:( 1 )画轴的受力简图;( 2 )作内力图(弯矩图和扭矩图);( 3 )按三强度理论校核轴的强度。
26 ( 15 )
圆轴直径 ,已知 , , , 。求轴内危险截面主应力和最大剪应力。
13.图示预应力简支梁。已知: , , 。求:
(1) 、 分别作用时,跨中截面的 , ,并绘相应的正应力分布图;
(2) 、 同时作用时,跨中截面的 , ,并绘相应的正应力分布图;
(3) 、 值不变,欲使 、 同时作用时,跨中底部正应力为零,有什么办法?
14.托架如图,已知AB为矩形截面梁,宽度 ,高度 ,杆CD为圆管,其外径 ,内径 ,材料的 。若不考虑CD杆的稳定问题,试按强度要求计算该结构的许可载荷 。
15.传动轴AB直径 ,轴长 , ,轮缘挂重 ,与转矩 平衡,轮直径 。试画出轴的内力图,并用第三强度理论校核轴的强度。
16.图示传动轴,B轮皮带张力铅垂方向,D轮皮带张力沿水平方向,B、C两轮直径为D= 600mm。轴的 , 。按第三强度理论确定轴的直径。
17.图示圆截面杆受横向力 和转矩 联合作用。今测得A点轴向应变 ,和B点与母线成 方向应变 。已知杆的抗弯截面模量 。 , , 。试用第三强度理论校核杆的强度。
(A) < < ;( B ) < = ;
( C ) < < ;( D ) = < ;
正确答案是________________。
05.一空间折杆受力如图所示,则AB杆的变形有四种答案:
(A)偏心拉伸;( B )纵横弯曲;( C )弯扭组合;( D )拉弯扭组合;
正确答案是__________________。
10.悬臂梁AB,A端固定,B端自由,在B端作用横向集中力 ,横截面形状和 力作用线如图所示。请回答将产生什么变形
( a ); ( b );
( c ); ( d );
11.结构如图,折杆AB与直杆BC的横截面面积为 , , 。求此结构的许用载荷 。
12.混凝土柱受力如图,已知 , , ,柱宽 ,若要求柱子横截面内不出现拉应力,求 值。
(1)试给出立柱AB的内力图;
(2)设许用应力 ,试为立柱选择圆截面直径。
计算题:
ቤተ መጻሕፍቲ ባይዱ22.
切槽的正方形木杆,受力如图所示。求:1) m–m截面上的 、 ;2 )此 是削弱前的 值的几倍。
23.图示结构,AB为矩形截面等直梁,C、D、E各点均为铰结,试求AB梁中的最大拉应力。
24.图示插刀刀杆的主切削力为 ,偏心矩为 ,刀杆直径为 。试求刀杆内的最大压应力与最大拉应力。(10分)
