资产管理-第9章 资本资产定价模型 精品
合集下载
资本资产定价模型PPT课件
资产定价的随机过程
随机过程的基本概念
随机过程是描述一系列随机事件的数学模型，其中每个事件的发生都具有不确定性。在资产定价的上下文中，随 机过程通常用于描述资产价格的变动。
资本资产定价模型的随机过程
资本资产定价模型假设资产价格的变动遵循随机过程，并且这种变动与资产的预期回报和风险有关。通过建立适 当的随机过程模型，可以进一步研究资产价格的动态行为和风险特征。
发展历程
起源
资本资产定价模型起源于20世纪60年代，由经济学家威廉·夏普、 约翰·林特纳和简·莫辛共同发展。
发展
在随后的几十年中，CAPM经历了多次修订和完善，以适应金融市 场的变化。
应用
资本资产定价模型被广泛应用于投资组合管理、风险评估和资本预算 等领域。
发展历程
起源
资本资产定价模型起源于20世纪60年代，由经济学家威廉·夏普、 约翰·林特纳和简·莫辛共同发展。
发展
在随后的几十年中，CAPM经历了多次修订和完善，以适应金融市 场的变化。
应用
资本资产定价模型被广泛应用于投资组合管本资产定价模型用于确定投资 组合的风险和预期回报，帮助投 资者在风险和回报之间做出权衡。
风险评估
通过CAPM，投资者可以评估特 定资产或投资组合的风险，并与 其他资产或基准进行比较。
主要发现
是一种用于评估风险和预期回报之间关系的金融模型，主要用于投资组合管理 和风险评估。
CAPM的核心思想
资本的预期收益率由两部分组成，一部分是无风险利率，另一部分是风险溢价， 即风险超过无风险资产的部分。
目的和目标
目的
通过理解CAPM，投资者可以更准确 地评估投资的风险和预期回报，从而 做出更明智的投资决策。
资本资产定价模型CAPM
而由于
M
Cov(rM , rM )
2 M
2 1
M
2 M
,
这也意味着所有资产的加权平均β 值为 1。如果市场的β 值为 1，那么市场是整个 经济市场中所有财产的投资组合，所有财产的加权β 值必定为 1。因此如果β 值大于 1，那么就意味着投资于高β 值的项目必须承担高于市场平均波动敏感度的风险。 另外，人们都习惯于认为管理好的公司将会提供高的投资回报。如果通过投资厂 房和设备的收益来衡量一个公司的收益水平的高低，那么这种测度方法是有效的。但 资本资产定价模型是在公司证券投资的基础上所作的收益预测。
w1E(r1 ) w1rf w11[ E(rM ) rf ] w2 E(r2 ) w2 rf w2 2[ E(rM ) rf ]
+ …=…
wn E(rn ) wn rf wn n[ E(rM ) rf ] E(rp ) rf p [ E(rM ) rf ]
9-13
证券市场线
可以把期望收益-贝塔关系视为收益-风险等式。因为β 值与最优风险投资组合方差的贡献度成比例的。所以证 券的β 值是测试其风险的适当指标。 单个资产的期望收益或风险溢价取决于其对投资组合风 险的贡献程度。股票的β 值衡量了股票对市场投资组合 方差的贡献度。因此可以预测到，对于任何资产或投资 组合而言，都要求风险溢价是关于β 的函数。CAPM论证 认为证券的风险溢价为β [E(rM)-rf]。 期望收益-贝塔关系曲线就是证券市场线(SML)。因为市 场的β 值为1，其斜率为市场投资组合的风险溢价(注意 不再是β ，β 是随不同股票而变动的)。横轴为β ，纵 轴为期望收益，当横轴上β =1时，这一点就是市场投资 组合的期望收益率。
M
Cov(rM , rM )
2 M
2 1
M
2 M
,
这也意味着所有资产的加权平均β 值为 1。如果市场的β 值为 1，那么市场是整个 经济市场中所有财产的投资组合，所有财产的加权β 值必定为 1。因此如果β 值大于 1，那么就意味着投资于高β 值的项目必须承担高于市场平均波动敏感度的风险。 另外，人们都习惯于认为管理好的公司将会提供高的投资回报。如果通过投资厂 房和设备的收益来衡量一个公司的收益水平的高低，那么这种测度方法是有效的。但 资本资产定价模型是在公司证券投资的基础上所作的收益预测。
w1E(r1 ) w1rf w11[ E(rM ) rf ] w2 E(r2 ) w2 rf w2 2[ E(rM ) rf ]
+ …=…
wn E(rn ) wn rf wn n[ E(rM ) rf ] E(rp ) rf p [ E(rM ) rf ]
9-13
证券市场线
可以把期望收益-贝塔关系视为收益-风险等式。因为β 值与最优风险投资组合方差的贡献度成比例的。所以证 券的β 值是测试其风险的适当指标。 单个资产的期望收益或风险溢价取决于其对投资组合风 险的贡献程度。股票的β 值衡量了股票对市场投资组合 方差的贡献度。因此可以预测到，对于任何资产或投资 组合而言，都要求风险溢价是关于β 的函数。CAPM论证 认为证券的风险溢价为β [E(rM)-rf]。 期望收益-贝塔关系曲线就是证券市场线(SML)。因为市 场的β 值为1，其斜率为市场投资组合的风险溢价(注意 不再是β ，β 是随不同股票而变动的)。横轴为β ，纵 轴为期望收益，当横轴上β =1时，这一点就是市场投资 组合的期望收益率。
投资学第章资本资产定价模型剖析ppt课件
比较CAPM：E(ri ) rf i[E(rM ) rf ]
与指数模型的期望形式：
E(ri ) rf i i[E(rM ) rf ] 可知二者差别在于，CAPM认为所有的i都为0。 市场模型：rf E(ri ) i[rf E(rM )] ei
如果CAPM有效，则市场模型等同于指数模型。
E(Ri ) kE(Ci ) ( L1 L2 L3 )
其中，E(Ci )为期望流动性代价； k为所有资产的调整后的平均持有期
为平均市场流动性的市场风险溢价净值 为系统性市场风险敏感度， L1、 L 2、 L3为流动性 E(RM CM )，CM 表示市场平均流动性溢价。
37
流动性的三要素
25
9.3 CAPM符合实际吗？
CAPM的实用性取决于证券分析。 9.3.1 CAPM能否检验 ▪ 规范方法与实证方法 ▪ 实证检验的两类 错误(数据、统计方法) 9.3.2 实证检验质疑CAPM
26
9.3 CAPM符合实际吗？
9.3.3CAPM的经济性与有效性 ▪ CAPM在公平定价领域的广泛应用 ▪ CAPM被普遍接受的原因 9.3.4 投资行业与CAPM的有效性 投资公司更趋向于支持CAPM
39
27
9.4 计量经济学和期望收益-贝塔关系
▪ 计量经济方法可能是引起CAPM被错误拒 绝的原因
▪ 相关改进
➢ 用广义最小二乘法处理残差相关性 ➢ 时变方差模型ARCH
28
9.5 CAPM的拓展形式
两种思路： ▪ 假定的放宽 ▪ 投资者心理特征的应用
29
9.5.1 零模型
有效前沿的三大性质：
▪ 两种有效前沿上的资产组合组成的任意资产组合仍在有 效前沿上
23
9.2.2 指数模型和已实现收益
与指数模型的期望形式：
E(ri ) rf i i[E(rM ) rf ] 可知二者差别在于，CAPM认为所有的i都为0。 市场模型：rf E(ri ) i[rf E(rM )] ei
如果CAPM有效，则市场模型等同于指数模型。
E(Ri ) kE(Ci ) ( L1 L2 L3 )
其中，E(Ci )为期望流动性代价； k为所有资产的调整后的平均持有期
为平均市场流动性的市场风险溢价净值 为系统性市场风险敏感度， L1、 L 2、 L3为流动性 E(RM CM )，CM 表示市场平均流动性溢价。
37
流动性的三要素
25
9.3 CAPM符合实际吗？
CAPM的实用性取决于证券分析。 9.3.1 CAPM能否检验 ▪ 规范方法与实证方法 ▪ 实证检验的两类 错误(数据、统计方法) 9.3.2 实证检验质疑CAPM
26
9.3 CAPM符合实际吗？
9.3.3CAPM的经济性与有效性 ▪ CAPM在公平定价领域的广泛应用 ▪ CAPM被普遍接受的原因 9.3.4 投资行业与CAPM的有效性 投资公司更趋向于支持CAPM
39
27
9.4 计量经济学和期望收益-贝塔关系
▪ 计量经济方法可能是引起CAPM被错误拒 绝的原因
▪ 相关改进
➢ 用广义最小二乘法处理残差相关性 ➢ 时变方差模型ARCH
28
9.5 CAPM的拓展形式
两种思路： ▪ 假定的放宽 ▪ 投资者心理特征的应用
29
9.5.1 零模型
有效前沿的三大性质：
▪ 两种有效前沿上的资产组合组成的任意资产组合仍在有 效前沿上
23
9.2.2 指数模型和已实现收益
09资本市场均衡模型：资本资产定价模型
第 9 章 资本市场均衡模型：资本资产定价模型 9.1 CAPM 的假设 资本资产定价模型（Capital Assets Pricing Model, 简称 CAPM）是用来解释均衡市 场中风险资产收益率的如何决定问题的。 资产组合理论虽然从理论上解决了如何构造投资组合的问题，但是这一过程相当繁杂， 需要大量的计算， 和一系列严格的假设条件。 这样就使得这一理论在实际操作上具有一定的 困难。 投资者需要一种更为简单的方式来进行处理投资事宜。 于是资本资产定价模型就产生 了。CAPM 模型是由美国学者 Sharpe 于 1964 年提出的，这个模型仍然以证券组合理论为基 础，在分析风险和收益的关系时，提出资产定价的方法和理论。对 CAPM 模型做出贡献的学 者有： 马科维茨（Harry M.Markowitz，美国，1927-） ，1952 年， 《资产组合选择：有效的多 样化》 。 特雷诺（Treynor，美国） ，1961 年。 威廉•夏普（William F.Sharpe, 美国 1934-） ，1964 年。 林特纳（Lintner，美国） ，1966 年。 默森（Mossion，美国） ，1966 年《Equilibrium in a Capital Asset Market》 。 资本资产定价模型（ CAPM ）是近代金融学的奠基石。 1952 年，马柯维茨（ Herry M. Markowitz）在其博士论文《投资组合的选择》一文中首先提出建立现代资产组合管理的理 论，12 年后，威廉•夏普（William Sharpe） 、约翰•林特纳（John Lintner）与简•莫辛（Jan Mossin）将其发展成资本资产定价模型。 它有如下这些基本的假设： （1）所有投资行为仅仅发生在一个时点上，即在 0 时刻决策，在 1 时刻收获； （2）投资者厌恶厌恶，并总是根据均值方差效率原则进行决策； （3）无摩擦的市场（frictionless market） ，即不存在交易费用和税收，所有证券无 限可分； （4）无操纵的市场（no manipulation） ，任何单独的投资者行为，都不足以影响资产 的市场价格，他们都是价格的接受者（price taker） ； （5）无制度限制（institutional restriction） ，允许卖空，并且可以自由支配卖空 所得。
第九章资本资产定价模型（CAPM）与因素模型
第九章资本资产定价模型（CAPM）与因素模型资本资产的定价是资本理论中最核心的问题，在资本市场中，几乎所有问题的研究都是与定价问题的研究相关。
自从20世纪50年代马科维茨提出证券投资组合理论以后，近半个世纪以来，可以说资本资产定价问题是现代金融理论研究中吸引学者最多和研究成果最多的研究领域。
资本资产定价模型（Capital Asset Pricing Model ，CAPM）是由夏普（Sharpe）、林特（Linter）和莫森（Mossin）等人在马科维茨理论的基础上创立的，成为现代金融学的基石，它给出了风险资产的期望收益率及其风险之间精确预测。
不过，这个模型应用的一个根本性的障碍在于模型所需要的参数：每种资产的均值及资产之间的协方差。
这些参数值不能直接获得，只能利用历史数据采取一定的估计方法进行估计来间接地获得，当资产数目较多时，计算量非常大，精确度也是一个问题。
在本章后半部分，我们介绍的因素模型（Factor Model）避免了在解释资产的收益时所必须面临的大量参数估计问题。
在因素模型的基本思想启发下，一种新的资产定价模型——套利定价理论（Arbitrage Pricing Theory ，APT）产生了。
APT是由罗斯（Ross）于1976年提出的。
他试图提出一种比传统CAPM更好的解释资产定价的理论模型，经过几十年的发展，APT在资产定价理论中的地位已不亚于CAPM。
第一节资本资产定价模型（CAPM）一、资本资产定价模型的基本假设资本资产定价模型是在理想的，称之为完善的资本市场中建立的。
它的基本假设是：1.所有投资者对一个证券组合以一期的期望回报率和标准差来评价此组合。
2. 投资者具有不满足性。
因此当面临其他条件相同的两种选择时，他们将选择具有较高预期回报率的那一种。
3. 投资者都是风险厌恶者。
因此当面临其他条件相同的两种选择时，他们将选择具有较小标准差的那一种。
4. 任何一种资产都是无限可分的。
第9讲_资本资产定价模型
四、资本资产定价模型（一）资本资产定价模型的基本原理必要收益率=无风险收益率+风险收益率，即：R=Rf+β×（Rm-Rf）Rf表示无风险收益率，以短期国债的利率来近似替代；Rm表示市场组合收益率，通常用股票价格指数收益率的平均值或所有股票的平均收益率来代替；β表示该资产的系统风险系数；（Rm-Rf）称为市场风险溢酬；β×（Rm-Rf）称为资产风险收益率。
【提示】（Rm-Rf）称为市场风险溢酬①它是附加在无风险收益率之上的，由于承担了市场平均风险所要求获得的补偿，它反映的是市场作为整体对风险的平均“容忍”程度，也就是市场整体对风险的厌恶程度。
②对风险越是厌恶和回避，要求的补偿就越高，市场风险溢酬的数值就越大。
③如果市场的抗风险能力强，则对风险的厌恶和回避就不是很强烈，要求的补偿就越低，所以市场风险溢酬的数值就越小。
【2017年·单选题】2016年，MULTEX公布的甲公司股票的β系数是1.15，市场上短期国库券利率为3%、标准普尔股票价格指数的收益率是10%，则2016年甲公司股票的必要收益率是（）。
A.10.50%B.11.05%C.10.05%D.11.50%【答案】B【解析】本题考查的知识点是资本资产定价模型中的必要收益率的计算，必要收益率=3%+1.15×（10%-3%）=11.05%，所以本题选项B正确。
【2016年·单选题】下列关于市场风险溢酬的表述中，错误的是（）。
A.市场风险溢酬反映了市场整体对风险的平均容忍度B.若市场抗风险能力强，则市场风险溢酬的数值就越大C.市场风险溢酬附加在无风险收益率之上D.若市场对风险越厌恶，则市场风险溢酬的数值就越大【答案】B【解析】若市场抗风险能力强，则对风险的厌恶和回避就不是很强烈，市场风险溢酬的数值就越小，所以选择选项B。
【2015年·多选题】下列关于资本资产定价模型的表述中，正确的有（）。
9_资本资产定价模型
9.1 资本市场线
资本市场线
G：将一部分资金投资于无风险资产，其余的投资于风 险证券。
CML 有效前沿
E(R )
曲线 差异 无
G
Rf
M
σp
13
第9讲 资本资产定价模型(CAPM)
9.1 资本市场线
资本市场线
H：将所有资金投资于市场证券组合 M，此时投资者可 得到市场平均收益率。
曲线 差异 无
CML 有效前沿
11
第9讲 资本资产定价模型(CAPM)
9.1 资本市场线
资本市场线
• 不同投资者可在资本市场线上找到由各种无风险和 风险资产组成的证券组合，并运用无差异曲线和资 本市场线确定最优投资组合。 F：将所有资金投资于无风险资产。 E(R )
差异 无 曲线
Rf
CML 有效前沿
M
F
σp
第9讲 资本资产定价模型(CAPM)
如果β系数为 1，意味着该证券与整个市场具有 相同的不可避免风险。 当β系数小于1时，情况恰恰相反，该证券的不 可避免风险小于整个市场风险。
这类证券（如公用事业、食品工业类股票）被称为防 守型的证券，因为这类证券的价格在市场价格上升时 ，其上涨率往往比市场的要低，但在市场价格下跌时 其下降率也往往较小。
上式便是著名的资本资产定价模型 （ Capital Asset Pricing Model，CAPM)
σ iM 2 σM
25
第9讲 资本资产定价模型(CAPM)
9.3 CAPM
CAPM
证券市场的均衡过程：
随着对某些证券的需求增加，导致其价格上升，从 而降低其期望收益； 反之，其他证券的需求不足，将导致其价格下跌， 从而提高其期望收益。 这一过程将持续到所有证券形成一个单一的风险价 格，投资者将无差异于它们。
资本资产定价模型CAPM.pptx
0.0205
14.3%
债券基金
回报率 离标差准平差方
17%
1.00%
7%
0.00%
-3%
1.00%
7.00%
0.0067
8.2%
14.3% 0.0205
9
第10页/共73页
协方差
衡量资产同步变动的程度
考虑如下的乘积：
[r股票(s)-E(r股票)][r债券(s)-E(r债券)]
协方差的定义
Cov(r股票,r债券) = S P(s)[r股票(s)-E(r股票)][r债券(s)-E(r债
26
第27页/共73页
10.4 两个资产的有效集
股票在组合的比率
0% 5% 10% 15% 20% 25% 30% 35% 40% 45% 50.00% 55% 60% 65% 70% 75% 80% 85% 90% 95% 100%
风险
8.2% 7.0% 5.9% 4.8% 3.7% 2.6% 1.4% 0.4% 0.9% 2.0% 3.08% 4.2% 5.3% 6.4% 7.6% 8.7% 9.8% 10.9% 12.1% 13.2% 14.3%
0.00%
-3%
1.00%
7.00%
0.0067
8.2%
2.05% 1 (3.24% 0.01% 2.89%) 3
8
第9页/共73页
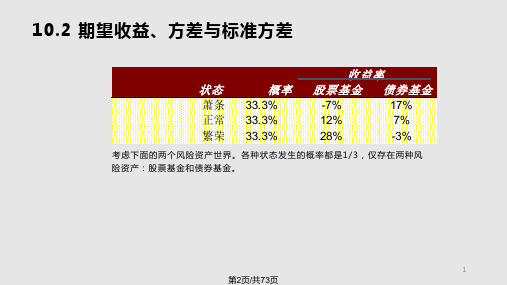
10.2 期望收益、方差与标准方差
状态
萧条 正常 繁荣
期望收益 方差 标准差
股票基金
回报率 离标差准平差方
-7%
3.24%
12%
0.01%
28%
2.89%
11.00%
24
第25页/共73页
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
• Market portfolio contains all securities and the proportion of each security is its market value as a percentage of total market value 市场组合包含所有证券并且每一证券作为总市 场价值的一部份是其市场价值
• Risk premium on an individual security is a function of its covariance with the market
Figure 9.1 The Efficient Frontier and the Capital Market Line
Using GE Text Example 通用电器公司为例
• Covariance of GE return with the market portfolio:
Cov(rGE
,
rM
)
Cov
rGE
,
n
wk
rk
n
wkCov(rk , rGE )
k 1
k 1
• Therefore, the reward-to-risk ratio for
• Derived using principles of diversification with simplified assumptions 它通过使用分散化和简化假设而来
• Markowitz, Sharpe, Lintner and Mossin are researchers credited with its development 此模型由马科维茨,夏普,林特纳和莫森研究
有效前沿和资本市场线
Market Risk Premium 市场风险溢价
•The risk premium on the market portfolio will be proportional to its risk and the degree of risk aversion of the investor:
E(rM ) rf
A
2 M
where
2 M
is the variance of the market portolio and
A is the average degree of risk aversion across investors
Return and Risk For Individual Securities 单个证券收益和风险
• There are homogeneous expectations 同质期望
Resulting Equilibrium Conditions 均衡条件
• All investors will hold the same portfolio for risky assets – market portfolio 所以投资者持有相同风险资产组合-市场组合
Using GE Text Example Continued
续例
• Reward-to-risk ratio for investment in
market portfolio:
Market risk premium Market variance
Assumptions 假设
• Individual investors are price takers 个人投资者是价格接受者
• Single-period investment horizon 投资持有期都相同：单期投资
• Investments are limited to traded financial assets 投资范围仅限于金融市场上的交易资产
• An individual security’s risk premium is a function of the covariance of returns with the assets that make up the market portfolio
• 单个证券的风险溢价是该资产收益与市场组合 收益的协方差的函数
• The risk premium on individual securities is a function of the individual security’s contribution to the risk of the market portfolio
单个证券的风险溢价取决于单个证券对投资组 合风险的贡献程度
investments in GE would be:
GE's contribution to risk premium wGE E(rGE ) rf E(rGE ) rf
GE's contribution to variance
wGECov(rGE , rM ) Cov(rGE , rM )
• No taxes and transaction costs 无所得税和交易税
Assumptions Continued 假设（续）
• Information is costless and available to all investors 信息由投资者共享
• Investors are rational mean-variance optimizers 投资者是理性的, 追求均值方差最优者
Resulting Equilibrium Conditions Continued
均衡条件续
• Risk premium on the market depends on the average risk aversion of all market participants 市场风险溢价取决于所有市场参与者的平均风 险厌恶水平
CHAPTER 9
资本资产定价模型
Capital Asset Pricing Model (CAPM) 资本资产定价模型
• It is the equilibrium model that underlies all modern financial theory 它是一种均衡模型,是现代金融理论的基石
• Risk premium on an individual security is a function of its covariance with the market
Figure 9.1 The Efficient Frontier and the Capital Market Line
Using GE Text Example 通用电器公司为例
• Covariance of GE return with the market portfolio:
Cov(rGE
,
rM
)
Cov
rGE
,
n
wk
rk
n
wkCov(rk , rGE )
k 1
k 1
• Therefore, the reward-to-risk ratio for
• Derived using principles of diversification with simplified assumptions 它通过使用分散化和简化假设而来
• Markowitz, Sharpe, Lintner and Mossin are researchers credited with its development 此模型由马科维茨,夏普,林特纳和莫森研究
有效前沿和资本市场线
Market Risk Premium 市场风险溢价
•The risk premium on the market portfolio will be proportional to its risk and the degree of risk aversion of the investor:
E(rM ) rf
A
2 M
where
2 M
is the variance of the market portolio and
A is the average degree of risk aversion across investors
Return and Risk For Individual Securities 单个证券收益和风险
• There are homogeneous expectations 同质期望
Resulting Equilibrium Conditions 均衡条件
• All investors will hold the same portfolio for risky assets – market portfolio 所以投资者持有相同风险资产组合-市场组合
Using GE Text Example Continued
续例
• Reward-to-risk ratio for investment in
market portfolio:
Market risk premium Market variance
Assumptions 假设
• Individual investors are price takers 个人投资者是价格接受者
• Single-period investment horizon 投资持有期都相同：单期投资
• Investments are limited to traded financial assets 投资范围仅限于金融市场上的交易资产
• An individual security’s risk premium is a function of the covariance of returns with the assets that make up the market portfolio
• 单个证券的风险溢价是该资产收益与市场组合 收益的协方差的函数
• The risk premium on individual securities is a function of the individual security’s contribution to the risk of the market portfolio
单个证券的风险溢价取决于单个证券对投资组 合风险的贡献程度
investments in GE would be:
GE's contribution to risk premium wGE E(rGE ) rf E(rGE ) rf
GE's contribution to variance
wGECov(rGE , rM ) Cov(rGE , rM )
• No taxes and transaction costs 无所得税和交易税
Assumptions Continued 假设（续）
• Information is costless and available to all investors 信息由投资者共享
• Investors are rational mean-variance optimizers 投资者是理性的, 追求均值方差最优者
Resulting Equilibrium Conditions Continued
均衡条件续
• Risk premium on the market depends on the average risk aversion of all market participants 市场风险溢价取决于所有市场参与者的平均风 险厌恶水平
CHAPTER 9
资本资产定价模型
Capital Asset Pricing Model (CAPM) 资本资产定价模型
• It is the equilibrium model that underlies all modern financial theory 它是一种均衡模型,是现代金融理论的基石