电子科技大学随机信号分析CH5习题及答案
西安电子科技大学 电院 《随机信号分析》大作业
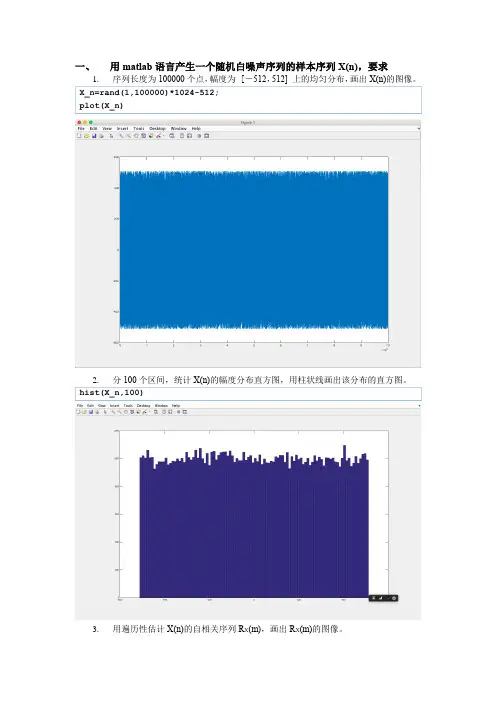
一、用matlab语言产生一个随机白噪声序列的样本序列X(n),要求
3.用遍历性估计X(n)的自相关序列R X(m),画出R X(m)的图像。
二、将一中产生的序列通过一个线性系统,其单位脉冲响应为h(n)=0.9n,n=0,
1,…,100
三、比较X(n)与Y(n)的幅度分布直方图,发生了什么变化。
分析其变化的原
因。
随机信号经过线性系统后,不会增加新的频率分量,但是输出的幅度和相位会发生变化。
白噪声X(n)的幅度基本相同,而Y(n)的幅度基本呈正态分布。
因为均匀白噪声是一种宽带非正态过程,所以通过一有限带宽线性系统后,输出Y(n)近似呈正态分布。
——via 1402011 赵春昊。
随机信号分析(第3版)第五章习题及答案

5.1 求题图5.1中三个电路的传输函数(不考虑输出负载)。
RRC1C 2C 1C 2C 1R 2R题图5.1解根据电路分析、信号与系统的知识, 第一个图中系统的传输函数 1/1()1/1j C H j R j C j RCωωωω==++ 第二个图中系统地传输函数 ()21112211/1()/11/1/j C j RC H j R j C j R C C j C R j C ωωωωωωω+==++++ 第三个图中系统地传输函数()2222212111221212121122/1/()//1/1/R j C R j C R j R R C H j R j C R j C R R j R R C C R j C R j C ωωωωωωωωω++==++++++5.2若平稳随机信号)(t X 的自相关函数||2)(ττ-+=BeA R X ,其中,A 和B 都是正常数。
又若某系统冲击响应为()()wth t u t te -=。
当)(t X 输入时,求该系统输出的均值。
解: 因为[]()22X EX R A =∞=所以[]E X A A =±=±。
()()()()()20wt A E Y t E h X t d E X t h d A te dt wξξξξξ∞∞∞--∞-∞±⎡⎤=-==±=⎡⎤⎡⎤⎣⎦⎣⎦⎢⎥⎣⎦⎰⎰⎰ 5.35.4 若输入信号00()cos()X t X t ω=++Φ作用于正文图5.2所示RC 电路,其中0X 为[0,1]上均匀分布的随机变量,Φ为[0,2π]上均匀分布的随机变量,并且0X 与Φ彼此独立。
求输出信号Y(t)的功率谱与相关函数。
解:首先我们求系统的频率响应()H j ω。
根据电路分析、信号与系统的知识,/1/11()()()1/1t RCj C H j h t e u t R j C j RCRCωωωω-==↔=++ 然后,计算)(t X 的均值与自相关函数,[]()1/2X m E X t ==[]{}(){}{}0000(,)cos cos X R t t EXt X t τωωτ+=++Φ+++Φ=⎡⎤⎣⎦()01/31/2cos ωτ+可见)(t X 是广义平稳的。
(完整word版)随机信号分析习题.(DOC)

随机信号分析习题一1. 设函数⎩⎨⎧≤>-=-0 ,0 ,1)(x x e x F x ,试证明)(x F 是某个随机变量ξ的分布函数.并求下列概率:)1(<ξP ,)21(≤≤ξP 。
2. 设),(Y X 的联合密度函数为(), 0, 0(,)0 , otherx y XY e x y f x y -+⎧≥≥=⎨⎩, 求{}10,10<<<<Y X P 。
3. 设二维随机变量),(Y X 的联合密度函数为⎥⎦⎤⎢⎣⎡++-=)52(21exp 1),(22y xy x y x f XY π 求:(1)边沿密度)(x f X ,)(y f Y(2)条件概率密度|(|)Y X f y x ,|(|)X Y f x y4. 设离散型随机变量X 的可能取值为{}2,1,0,1-,取每个值的概率都为4/1,又设随机变量3()Y g X X X ==-。
(1)求Y 的可能取值 (2)确定Y 的分布. (3)求][Y E 。
5. 设两个离散随机变量X ,Y 的联合概率密度为:)()(31)1()3(31)1()2(31),(A y A x y x y x y x f XY --+--+--=δδδδδδ试求:(1)X 与Y 不相关时的所有A 值。
(2)X 与Y 统计独立时所有A 值。
6. 二维随机变量(X ,Y )满足:ϕϕsin cos ==Y Xϕ为在[0,2π]上均匀分布的随机变量,讨论X ,Y 的独立性与相关性。
7. 已知随机变量X 的概率密度为)(x f ,求2bX Y =的概率密度)(y f .8. 两个随机变量1X ,2X ,已知其联合概率密度为12(,)f x x ,求12X X +的概率密度?9. 设X 是零均值,单位方差的高斯随机变量,()y g x =如图,求()y g x =的概率密度()Y f y\10. 设随机变量W 和Z 是另两个随机变量X 和Y 的函数222W X Y Z X⎧=+⎨=⎩ 设X ,Y 是相互独立的高斯变量。
《随机信号分析》-高新波等-课后答案

C = *第0章1/1;1/ 2;1/ 3;1/4;1/ 5;1/ 6;2 /1;2 / 2;2 / 3;2 /4;2 / 5;2/6;3/l;3/2;3/3;3/4;3/5;3/6;4/l;4/2;4/3;4/4;4/5;4/6;5/l;5/2;5/3;5/4;5/5;5/6;6/l;6/2;6/3;6/4;6/5;6/64 = {l/l;2/2;3/3;4/4;5/5;6/6}1/5;!/ 6;2 /4;2 / 5;2 / 6;3 / 3;3 / 4;3 / 5;3 / 6;4 / 2;4 / 3;4 / 4;4 / 5;'4/6;5/l;5/2;5/3;5/4;5/5;5/6;6/l;6/2;6/3;6/4;6/5;6/6 /1 /1;1 / 2;1 / 3;1 / 4;1 / 5;1 / 6;2 /1;2 / 2;2 / 3;2 / 4;2 / 5;2 / 6;3 /1;3 / 2;'3/3;3/4;3/5;3/6;4/l;4/2;4/3;5/l;5/2;5/3;6/l;6/2;6/3B =0.2(2)'0用)=x < 00<x<30x 2/12 2x -3-x 2/4,3<x <41 x>4P (l<x<7/2)=f^v +⑴⑶0.3E (X )= L 2<T :t/r = £ ~^y %dy =E (X2)=「Ji 奇dx = 了241a\^e~y 晶尸dy = 2a 2r (2)= 2a 2o(x)=£(/)-(研x))2=2尸_m S=04292S 0.4⑴£(Jf)=(-1)x03+0x0.44-1x03=0£(K)=1x0.4+2x0.2+3x0.4=2(2)由于存在X=0的情况,所以研Z)不存在(3)E(Z)=(-1-1)2x0.2+(-1-2)2xO.l+(O-l)2xO.l+(0-3)2x0.3+(l-l)2xO.1+0-2)2x0.1+(1-3)2x0.1=5 0.5X=ln*,当\dy\=^M=^e(Iny-mf2/”00.6t2+勺血s=£0<x<l,0<.y<2f32\X x~.—+—s as=(363-)7X*i X丁-312=诉号>=2尸号间=fp+导=土名/(x)0.7££be~^x+y^dxdy=[/>(1-e~'\~y dy=/>(1-e-,)= 1,/>=(!—e~x尸/(x)=he~x Ve-y dy=—^e~x fi<x<\f(y)=be~y^e~x dx—e~y,y>00.8(1)x,v不独立⑵F(z)=££~'|(X+yY{x+y}dxdy=£|/『(xe~x +ye~x}ixdy =g按(1一(1+Z一*片5+*(]_e-(z-y)肱,=]_]+z+/2\2f(z)=F'(z)=\+z+—e~:-(1+z)e~z=—e-2,z>0、2)20.9。
随机信号分析习题五

随机信号分析习题五:1. 非周期平稳过程()X t 的自相关函数为2()X R a be ττ-=+式中,a 和b 是正实常数,系统的冲激响应为()()t h t e U t -Ω=其中Ω为正实常数,求该系统输出过程的均值。
2. 假设低通滤波器的传输函数与冲激响应如下1()1H w jwRC =+,11()RCh t e RC-=输入为白噪声,其功率谱密度为0()2X G w N =,求 (1) 滤波器输出功率谱密度;(2) 滤波器输出自相关函数; (3) 证明322131321()()(),(0)Y Y Y Y R t t R t t R t t t t t R ---=>>3. 设有冲激响应为()h t 的线性系统,系统输入()X t 为零均值、平稳过程,该过程的自相关函数为()()X R τδτ=问:()h t 具备什么条件,可使输入过程()X t 与输出过程()Y t 在时刻1t t =的随机变量不相关。
4. 设n X 是纯随机序列,且在1+与1-间均匀分布,试利用下列滤波方程求出n W ,n Z 与nY 的自相关函数与功率谱密度。
1n n n W X X -=- 122n n n n Z X X X --=++112n n n Y Y X -=-+5. 线性系统()H j ω的输入为平稳过程()x t ,其功率谱为()x S ω,设()y t 为输出。
(1) 求误差过程()()()e t y t x t =-的功率谱密度函数()e S ω; (2) 考虑RC 电路,设输入为一个二元波过程,求()e S ω。
6. 一个平均电路如下图所示(1) 证明系统的冲激响应函数为1,0()0,t Th t others ≤≤⎧=⎨⎩ (2) 设输入过程()X t 的功率谱密度为()X S ω,求输出过程()Y t 的功率谱密度。
7. 设输入为白噪声过程()X t ,其自相关函数为0()()X R S τδτ=。
电子科技大学通信原理答案CH5(精品文档)

习题1. 已知某2ASK 系统的码元速率为1000波特,所用载波信号为()6cos 410A t π⨯。
(1) 假定比特序列为{0110010},试画出相应的2ASK 信号波形示意图; (2) 求2ASK 信号第一零点带宽。
解:由1000b s R R bps ==,6210cf Hz =⨯, 621020001000b c c b T f T R ⨯=== (1)一个码元周期内有2000个正弦周期:111{}n a ()2ASK s t 0(2)022000b B R Hz ==2.(mooc)某2ASK 系统的速率为2b R =Mbps ,接收机输入信号的振幅40μV A =,AWGN 信道的单边功率谱密度为180510N -=⨯W/Hz ,试求传输信号的带宽与系统的接收误码率。
解:传输信号的带宽24T b B R MHz ==,平均码元能量:24bb A T E =。
()()222100102cos 21cos 422,0,2bb T T b bc c b b b b A T A E A f t dt f t dt E E E E ππ==+=+==⎰⎰()2622618000401040444210510b b b E A T A N N R N --⨯====⨯⨯⨯⨯ 系统的接收误码率:(1) 若是非相干解调,非相干解调误码率公式,222200222BPFn b A A A R N B N σ===γ//24092( 5.11221 5.11.0306102)b E N e P e e e ----=≈==⨯γ4表 (2) 若是相干解调:由相干解调误码率公式得(最佳),1001.26981040b e E P Q Q N -⎛⎫===⎪⨯ ⎪ ⎝⎭也是MF 接收机的结果。
3. 某2FSK 发送“1”码时,信号为()()111sin s t A t ωθ=+,0s t T ≤≤;发送“0”码时,信号为()()000sin s t A t ωθ=+,0s t T ≤≤。
电子科技大学2009年随机信号分析试题A与标准答案
(1) 试判断 X ( t ) 和 Y ( t ) 在同一时刻和不同时刻的独立性、相关 性及正交性; (2) 试判断 X ( t ) 和 Y ( t ) 是否联合广义平稳。 解: (1) 由于 X ( t ) 和 Y( t ) 包含同一随机变量 θ ,因此非独立。 根据题意有
f (θ ) = 1 2π
π
−π
1 1 = cos[ w0 ( t1 − t2 )] cos( w0τ ) 2 2
同理可得 RY ( t1 ,t2 ) = RX ( t1 ,t2 ) ,因此 X ( t ) 和 Y( t ) 均广义平稳。
,t2 ) C XY ( t1= ,t2 ) 由于 RXY ( t1= 1 1 sin [w0 ( t1 − = t2 )] sin (w0τ ) ,因此 X ( t ) 和 2 2
。
π
−π
E[ X ( t )] E [sin(ω = = 0 t + Θ) ]
E[Y( t )] E [ cos(ω = = 0 t + Θ) ]
π
∫
1 sin( w0= t + θ )dθ 0 , 2π
−π
∫
1 cos( w0= t + θ )dθ 0 2π
C XY ( t1 ,t2 ) = RXY ( t1 ,t2 ) = E[ X ( t1 )Y( t2 )] = E[sin (w0t1 + θ )co s( w0t2 + θ )]
1 1 1 1 − τ 1 −3 τ = P R(0)= += R (τ )= e + e ,所以 4 12 3 4 12
1 ∞ 1 10 20 P S ( ) d 2 d = = = ω ω ω (3) 可以。 2π ∫−∞ 2π ∫−10 π
电子科大随机信号分析随机期末试题答案完整版
电子科大随机信号分析随机期末试题答案 HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】电子科技大学2014-2015学年第 2 学期期 末 考试 A 卷一、设有正弦随机信号()cos X t V t ω=,其中0t ≤<∞,ω为常数,V 是[0,1)均匀分布的随机变量。
( 共10分)1.画出该过程两条样本函数。
(2分)2.确定02t πω=,134t πω=时随机信号()X t 的一维概率密度函数,并画出其图形。
(5分)3.随机信号()X t 是否广义平稳和严格平稳?(3分)解:1.随机信号()X t 的任意两条样本函数如题解图(a)所示:2.当02t πω=时,()02X πω=,()012P X πω⎡⎤==⎢⎥⎣⎦,此时概率密度函数为:(;)()2X f x x πδω=当34t πω=时,3()42X πω=-,随机过程的一维概率密度函数为:3. ()[]1cos cos 2E X t E V t t ωω==⎡⎤⎣⎦ 均值不平稳,所以()X t 非广义平稳,非严格平稳。
二、设随机信号()()sin 2X n n πφ=+与()()cos 2Y n n πφ=+,其中φ为0~π上均匀分布随机变量。
( 共10分)1.求两个随机信号的互相关函数12(,)XY R n n 。
(2分)2.讨论两个随机信号的正交性、互不相关性与统计独立性。
(4分)3.两个随机信号联合平稳吗?(4分)解:1.两个随机信号的互相关函数其中()12sin 2220E n n ππφ++=⎡⎤⎣⎦2. 对任意的n 1、n 2 ,都有12(,)0XY R n n =,故两个随机信号正交。
又故两个随机信号互不相关,又因为故两个随机信号不独立。
3.两个随机信号的均值都平稳、相关函数都与时刻组的起点无关,故两个信号分别平稳,又其互相关函数也与时刻组的起点无关,因而二者联合平稳。
北邮随机信号答案ch5
怎样的条件才能使
Z (t ) =
∑A e ω
j k =1 k
n
kt
是一个复平稳随机过程。 5.7 设有复随机过程
Z (t ) = ∑ (α i cos ω i t + jβ sin ω i t )
i =1
n
其中 α i 与 β k 是相互独立的随机变量, α i 与 α k 、 β i 与 β k (i ≠ k ) 是相互正交的,数学期 望和方差分别为 E[α i ] = E[ β i ] =0, 解:
πτ
= R0 (τ ) cos ω0τ
ˆ (τ ) = R (τ ) sin ω τ 是一个低频信号,所以 R n 0 0 πτ ˆ (τ ) sin ω τ = R (τ ) 所以 Rn (τ ) = Rn (τ ) = Rn (τ ) cos ω0τ + R n 0 0
由于 R0 (τ ) =
c s
=
1 2π
∫
∞
−∞
[2 X (ω − ω ′)U (ω − ω ′)][2 X (ω ′)U (ω ′)]d ω ′
Ω Ω ⎧ ω0 − ≤ ω ′ ≤ ω0 + ⎪ Ω Ω ⎪ 2 2 时亦不 由于有 ω0 − ≤ ω ≤ ω0 + 时 X (ω ) 不为零,因此有 ⎨ 2 2 ⎪ω − Ω ≤ ω − ω ′ ≤ ω + Ω 0 0 ⎪ 2 2 ⎩
5.2 设 A(t ) 与 ϕ(t ) 为低频信号,证明 (1) H [ A(t ) cos[ω 0 t + ϕ (t )] = A(t ) sin[ω 0 t + ϕ (t )] (2) H [ A(t ) sin[ω 0 t + ϕ (t )] = − A(t ) cos[ω 0 t + ϕ (t )]
ch5FIR习题答案
5-2 解:
某三阶设 FIR 滤波器的系统函数 H1(z)为 H1 (z) = (6 − z−1 −12 z−2 )(2 + 5 z−1 )
(1)试确定幅度响应和 H1(z)相同的所有 FIR 滤波器的系统函数。 (2)上述 FIR 滤波器哪个是最大相位系统,哪个是最小相位系统?
5.6 习题 15.6来自习题5-1 设 F1(z)是线性相位 FIR 系统函数 H(z)的一个因子。试确定满足条件的最低阶的 H(z)。 (1) F1 (z) = 1 + 2 z −1 + 3z −2
(2) F1 (z) = 3 + 5z −1 − 4 z −2 − 2 z−3
解:设 F1 (z) = a + bz −1 + cz−2 ,则零点为其倒数的多项式 F2 (z) 为
记:L=M/2,则有
L
A(Ω ) = ∑ 2h[L − k]sin( kΩ ) k=1
H (e jΩ ) = e − j( M / 2) Ω e jπ/ 2 A(Ω )
5.6 习题 5
5-10 试证明式(5-16) 和式(5-17)。 证:
M
( M −1 ) / 2
M
H (e jΩ ) = ∑ h[k ]e − jkΩ = ∑ h[k ]e −jkΩ + ∑ h[k ]e −jkΩ
k =0
k=0
k=( M +1 )/ 2
令 l = M − k ,则有
所以
M
( M −1 ) / 2
( M −1) / 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5.1 求题图5.1中三个电路的传输函数(不考虑输出负载)。
R
R
C
1
C 2
C 1
C 2
C 1
R 2
R
题图5.1
解根据电路分析、信号与系统的知识, 第一个图中系统的传输函数
1/1
()1/1j C H j R j C j RC ωωωω==++
第二个图中系统地传输函数
()211
1221
1/1()/11/1/j C j RC H j R j C j R C C j C R j C ωωωωωωω+==
++++
第三个图中系统地传输函数
()
2222
1122
11222121
121212/1/()//1/1/R j C R j C H j R j C R j C R j C R j C R j R R C R R j R R C C ωωωωωωωωω+=
+
+++=
+++
5.2 若平稳随机信号)(t X 的自相关函数
|
|2)(ττ-+=Be A R X ,其中,A 和B 都是正
常数。
又若某系统冲击响应为()()wt h t u t te -=。
当)(t X 输入时,求该系统输出的均值。
解: 因为[]()2
2
X E X R A =∞=
所以[]E X A =±。
()2
1H j j w ωω⎛⎫= ⎪+⎝⎭ ()2
10H j w ⎛⎫= ⎪⎝⎭
()()()2
2
10A
E Y t E X t H j A w w ±⎛⎫==±⋅=⎡⎤⎡⎤ ⎪⎣⎦⎣⎦⎝⎭
5.3
5.4 若输入信号00()cos()X t X t ω=++Φ作用于正文图5.2所示RC 电路,其中0X 为[0,1]上均匀分布的随机变量,Φ为[0,2π]上均匀分布的随机变量,并且0X 与Φ彼此独立。
求输出信号Y(t)的功率谱与相关函数。
解:首先我们求系统的频率响应()H j ω。
根据电路分析、信号与系统的知识,
1/1
()1/1j C H j R j C j RC ωωωω==
++
然后,计算)(t X 的均值与自相关函数,
[][]00()cos()1/2X m E X t X t ω==++Φ=
(){}[]{}
{}()
00
00(,)cos cos 1/31/2cos X R t t E
X
t X
t τωτωωτ+=+++Φ++Φ⎡⎤⎣⎦
=+
可见)(t X 是广义平稳的。
考虑系统稳态时的
解,可利用推论得出
()[][]()2
002
002220()()()
21()()321()2()()2(1)3
Y X S S H j RC R C ωωωππδωδωωδωωωππ
δωωδωωδωω=⎧⎫
=+-++⨯⎨⎬+⎩⎭=-++++
于是,
02
2
2
01()cos 1/3
2(1)
Y R R C τωτω=
++
5.5
5.6 设某积分电路输入输出之间满足以下关系
()()t
t T
Y t X d ττ-=⎰
式中,T 为积分时间。
并设输入输出都是平稳过程。
求证输出功率谱密度为
2
2
4()
()sin 2X Y S T S ωωωω
⎛⎫=
⎪⎝⎭
(提示:()
(Y t X t h t
=*,而()()h t u t u t T =--,是矩形方波。
)
解:因为 ()()t
t T Y t X d ττ-=⎰ 所以()()()h t u t u t T =-- 而
()()()()0
/2
2sin /2T
j t
j t
j T H j h t e
dt h t e
dt
T e ωωωωωω
∞
---∞
-===⎰⎰
所以 ()
2
2
2
4sin 2T H j ωωω
⎛⎫ ⎪
⎝⎭=
所以
()2
2
2
4()
()()sin 2X Y X S T S S H j ωωωωωω
⎛⎫
==
⎪
⎝⎭
5.7 5.8 5.9
5.10 若线性时不变系统的输入信号()X t 是均值为零的平稳高斯随机信号,且自相关函数为()()X R τδτ=,输出信号为()Y t 。
试问系统()h t 要具备什么条件,才能使随机变量1()X t 与1()Y t 互相独立。
解: 由于输入信号()X t 是均值为零的平稳高斯随机信号,所以通过线性时不变系统后
()Y t 仍然是均值为零的平稳高斯随机信号,
且()X t 和()Y t 是高斯联合平稳过程。
如果
()
1X t 与
()
1Y t 相互独立,则
()()11[X t Y t ](0)0XY E R ==。
而
()()()()XY X R R h h ττττ=*-=-
因此,()h t 要满足()00h =。
5.11 若功率谱为5W/Hz 的平稳白噪声作用到冲击响应为()e ()at
h t u t -=的系统上,求系统的均方值与功率谱密度。
解:由题知:()1
H j j a ωω=+,
所以()()
2
22
2
255252Y a S H j a a a ωωωω===⋅++
而输出过程的自相关函数:
()52a Y R e a
τ
τ-=
于是,()()2
5
02Y E Y t R a ⎡⎤==⎣⎦
5.12
5.13 功率谱为02N 的白噪声作用到|(0)|2H =的低通网络上,网络的等效噪声带宽为2MHz 。
若噪声输出平均功率是0.1瓦,求0N 的值。
解:
由()2
000.1N N H B ⋅=得,
()
8
02
60.10.1 1.2510
2104
0N N B H -=
==⨯⨯⨯(瓦/Hz ) 5.14
5.15
5.16 已知平稳随机信号的相关函数为
(1) 2
1(1||),()10,X X R σαττα
ττα⎧-≤⎪⎪=⎨⎪>
⎪⎩
(2)2
||
()X X
R e
αττσ-=
求它们的矩形等效带宽。
解:(1)因为()X R τ是三角函数,
()222X
X S Sa σωωαα⎛⎫= ⎪⎝⎭
()()()()22
001
22022
X X X eq X X X S R B d S S ωασα
ωπ
ωσ∞
=
===⎰
(2)
2
||
()X X
R e αττσ-=
()()2
2
22j X X X S R e
d ωτ
σα
ωττωα∞
--∞==+⎰
所以
()()()()22
00122044
X X X eq X X X S R B d S S ωασα
ωπ
ωσ∞
=
===⎰。
