简谐近似和简正坐标
合集下载
简谐近似和简正坐标

N个原子的位移矢量 N个原子体系的势能函数在平衡位置按泰勒级数展开
取
平衡位置
—— 不计高阶项
系统的势能函数
V
1 2
i
3N , j1
(
2V
i
j
)0
i
j
03_01_简谐近似和简正坐标 —— 晶格振动与晶体的热学性质
系统的势能函数
系统的动能函数
系统的哈密顿量
H
1 2
3N i1
mi i 2
1 3N 2V (
只考察某一个振动模
系统能量本征值计算
i
aij mi
Qj
aij mi
Asin( jt )
正则动量算符
系统薛定谔方程
(1
2
3N i1
pi2
1 2
3N
i2Qi2 ) (Q1, Q3N )
i1
E (Q1,
Q3N )
03_01_简谐近似和简正坐标 —— 晶格振动与晶体的热学性质
任意一个简正坐标
(
)
—— 一个简正坐标对应一个谐振子方程,波函数是以简正 坐标为宗量的谐振子波函数
声子 —— 晶格振动的能量量子;或格波的能量量子
一个格波是一种振动模,称为一种声子,能量为
当这种振动模处于
时,说明有 个声子
03_01_简谐近似和简正坐标 —— 晶格振动与晶体的热学性质
晶格振动 —— 声子体系 —— 声子是一种元激发,可与电子或光子发生作用 —— 声子具有能量_动量,看作是准粒子 —— 晶格振动的问题 声子系统问题的研究 —— 每个振动模式在简谐近似条件下都是独立的 —— 声子系宗是无相互作用的声子气组成的系统
2 i, j1 i j
固体物理 5_1简谐近似和简震坐标

Qi A sin(i t )
i 晶格振动频率
Q j A sin( j t )
mi Qj aij mi A sin( j t ) aij
只考察某一个简振坐标 Q j 的振动
代入 m i i
a Q
j 1 ij
3N
j
i
i 1,23N
所有原子共同参与的一个振动称一个振动模
3N
1 即晶格振动能量即3N个谐振子能量和 En (ns ) s 2 s 1
n 0,1,2
晶格振动能量以 s为单位变化.
5-1简谐近似和简正坐标 —— 晶格振动与晶体的热学性质
2Q 0, i 1, 2, 3,3N Qi i i
标准谐振动方程
5-1简谐近似和简正坐标 —— 晶格振动与晶体的热学性质
2Q 0, i 1, 2, 3, 3N Qi i i
结论:
标准谐振动方程
—— 3N个独立无关的方程
晶体内原子(绕平衡位置)振动可看成3N个独立谐振子的振动 方程解
假设存在线性变换 mi ui
a Q
j 1 ij
3N
1 3N 2 T Qi 2 i 1
j
1 3N 2 2 V i Qi 2 i 1
1 3N 2 1 3N 2 2 系统的哈密顿量H T V Qi i Qi 2 i 1 2 i 1
1 3N 2 1 3N 2 2 系统的拉格朗日函数 L T V Qi i Qi 2 i 1 2 i 1
对第n个原子 偏离平衡位置的位移矢量 u (t ) n
uni (i 1,2,3)
N个原子的位移矢量 ui (t )
半导体光学7色散曲线
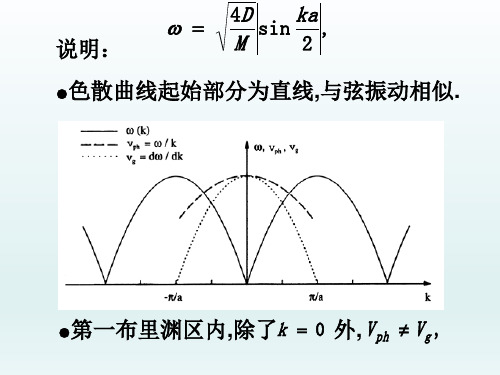
u2n ,0 u2n 2,0 AM , u2n 1,0 u2n 1,0 Am ..
将以上所设的方程的解代入运动方程,可
得以下方程组:
2D coskaAM 2D 2m Am 0. 2D 2M AM 2D coskaAm 0,
若 AM 0,Am 0 不存在,以上方程组的
动方程.因此,驻波不会沿z方向传播.群速
度为零,这表示驻波能量稳定!!!
●平移倒格矢 G
2l
a
l
取整),色散曲
线可以从第一布里渊区移到第一布里渊
区之外.但是,
k G
4D M
sin
k
G a
2
4D M
sin
k
2 a
2
l a
4D M
sin
ka
2l
2
4D M
sin
ka
2
k .
k k G 格波频率相同.
OP:GaAs,AlAs 不重叠,驻波.
满足 niai
m ,m
2
1,2,3 ;i
A,B .
kzm
2
2m 2niai
m
niai
,
m 1,2,3 ;i A,B .
AP:GaAs,AlAs 接近,为传播模.折叠效应
是界面处AP周期性多次反射相干叠加结果.
9.9 混晶中声子 1.混晶
2
D
1
m
1
M
D
1
m
1
M
,
12
D
1
m
1
M
D
1
m
1
M
2D
1
m
1
M
,光学支
将以上所设的方程的解代入运动方程,可
得以下方程组:
2D coskaAM 2D 2m Am 0. 2D 2M AM 2D coskaAm 0,
若 AM 0,Am 0 不存在,以上方程组的
动方程.因此,驻波不会沿z方向传播.群速
度为零,这表示驻波能量稳定!!!
●平移倒格矢 G
2l
a
l
取整),色散曲
线可以从第一布里渊区移到第一布里渊
区之外.但是,
k G
4D M
sin
k
G a
2
4D M
sin
k
2 a
2
l a
4D M
sin
ka
2l
2
4D M
sin
ka
2
k .
k k G 格波频率相同.
OP:GaAs,AlAs 不重叠,驻波.
满足 niai
m ,m
2
1,2,3 ;i
A,B .
kzm
2
2m 2niai
m
niai
,
m 1,2,3 ;i A,B .
AP:GaAs,AlAs 接近,为传播模.折叠效应
是界面处AP周期性多次反射相干叠加结果.
9.9 混晶中声子 1.混晶
2
D
1
m
1
M
D
1
m
1
M
,
12
D
1
m
1
M
D
1
m
1
M
2D
1
m
1
M
,光学支
4-3 简谐近似和

2)化简系统的动能和势能
动能
1 T m 2
n
2 n
1 1 m 2 Nm
1 2
n q
Q ( q )e inaq
q'
Q ( q ' )e inaq'
qq '
1 Q ( q ) Q ( q ' ) N
Department of Physics, Northwest University
Solid State Physics
由(5)式知,当只考察某一个 Qi 的振动时,(5)式可以化为
i
aij mi
A sin( it )
(12)
这表明,一般地说,一个简正振动并不是表示某一个原子的振动,而是表示 整个晶体所有原子都参与的振动,而且它们的振动频率都相同。由简正坐标所代 表的,体系中所有原子一起参与的共同振动,常称为一个振动模或简正模 (normal mode)。 由量子力学我们知道,用(9)式可以直接写出哈密顿算符和薛定谔方程
1 2 2 2 [ i Qi ] (Qi ) i (Qi ) 2 2 Qi
(14)
Department of Physics, Northwest University
Solid State Physics
谐振子方程的解为
i (ni )i
ni (Qi )
i 2l N
0
说明声子不是动量的携带者。
Department of Physics, Northwest University
1 e
Solid State Physics
03-02一维单原子链--(1)幻灯片

m2 当 q 0 sin(qa) qa
22
a / m q VEla q stic VElastic a /m
—— 格波的色散关系与连续介质中弹性波的一致
§3-2 一维单原子链 —— 晶格振动与晶体的热学性质
格波 —— 短波极限情况
q
a
2 /msin(aq)
2
max 2 /m
—— 格波的色散关系与连续介质中弹性波的不一致 —— 不同频率的格波传播速度不同
—— 格波的波形图 —— 向上的箭头代表 原子沿X轴向右振动 —— 向下的箭头代表 原子沿X轴向左振动
§3-2 一维单原子链 —— 晶格振动与晶体的热学性质
格波方程 格波波长
n Aei(tna)q
2 q
格波波矢 qv 2 nv
格波相速度
vp
q
不同原子间相位差 n'a qna (n q'n)aq
m2
a
频率极小值 min0
频率极大值 max 2 /m
0 q 02 /m
a
只有频率在 02 /m 之间的格波才能在晶体中传播,
其它频率的格波被强烈衰减 —— 低通滤波器
ωmax称为截止频率
§3-2 一维单原子链 —— 晶格振动与晶体的热学性质
格波 —— 长波极限情况 q0, a
2 sin(aq)
—— 实际的晶体为有限,形成的链不是无穷长,链两头 的原子不能用中间原子的运动方程来描述
§3-2 一维单原子链 —— 晶格振动与晶体的热学性质
—— N个原子头尾相接形成环链,保持所有原子等价特点 —— N很大,原子运动近似为直线运动 —— 处理问题时考虑
到环链的循环性
设第n个原子的位移 n
再增加N个原子之后
22
a / m q VEla q stic VElastic a /m
—— 格波的色散关系与连续介质中弹性波的一致
§3-2 一维单原子链 —— 晶格振动与晶体的热学性质
格波 —— 短波极限情况
q
a
2 /msin(aq)
2
max 2 /m
—— 格波的色散关系与连续介质中弹性波的不一致 —— 不同频率的格波传播速度不同
—— 格波的波形图 —— 向上的箭头代表 原子沿X轴向右振动 —— 向下的箭头代表 原子沿X轴向左振动
§3-2 一维单原子链 —— 晶格振动与晶体的热学性质
格波方程 格波波长
n Aei(tna)q
2 q
格波波矢 qv 2 nv
格波相速度
vp
q
不同原子间相位差 n'a qna (n q'n)aq
m2
a
频率极小值 min0
频率极大值 max 2 /m
0 q 02 /m
a
只有频率在 02 /m 之间的格波才能在晶体中传播,
其它频率的格波被强烈衰减 —— 低通滤波器
ωmax称为截止频率
§3-2 一维单原子链 —— 晶格振动与晶体的热学性质
格波 —— 长波极限情况 q0, a
2 sin(aq)
—— 实际的晶体为有限,形成的链不是无穷长,链两头 的原子不能用中间原子的运动方程来描述
§3-2 一维单原子链 —— 晶格振动与晶体的热学性质
—— N个原子头尾相接形成环链,保持所有原子等价特点 —— N很大,原子运动近似为直线运动 —— 处理问题时考虑
到环链的循环性
设第n个原子的位移 n
再增加N个原子之后
03_01简谐近似和简正坐标

1 En= n 2
n=0,1,2…… (3-57)
这表明谐振子处于不连续的能量状态。
1 ,称为零点能。 当n=0时,它处于基态,E0= 2
相邻状态的能量差为,它是谐振子的能量量子, 称它为声子 ,正如人们把电磁辐射的能量量子称 为光子一样。 3NS个格波与3NS个量子谐振子一一对应,因此式 (3-57)也是一个频率为ω的格波的能量。频率 为ωi(q)的格波被激发的程度,用该格波所具有的 能量为ωi (q)的声子数n的多少来表征。
2.声子是一种准粒子
声子与声子,声子与其它粒子、准粒子互作用, 满足能量守恒。 不具有通常意义下的动量,常把q称为声子的
粒子数不守恒,例如温度升高后声子数增加。
准动量。
3.准动量选择定则
准动量的确定只能准确到可以附加任何 一个倒格矢Gh
ω(q)= ω(q+ Gh) Ex: 二声子作用 q1+q2=q3+Gh q1+q2=q3+Gh
系统的势能函数
系统的动能函数
系统的哈密顿量 H
1 1 V 2 i ( mi ) 0 i j 2 i 1 2 i , j 1 i j
3N 3N 2
—— 含有坐标的交叉项
§3-1 简谐近似和简正坐标 —— 晶格振动与晶体的热学性质
引入简正坐标
—— 原子的坐标和简正坐标通过正交变换联系起来 假设存在线性变换
1 能量本征值 i ( ni ) i 2
本征态函数
—— 谐振子方程
n (Qi ) iຫໍສະໝຸດ iexp(
2
2
) H ni ( )
— 厄密多项式
§3-1 简谐近似和简正坐标 ——
晶格振动与晶体的热学性质
n=0,1,2…… (3-57)
这表明谐振子处于不连续的能量状态。
1 ,称为零点能。 当n=0时,它处于基态,E0= 2
相邻状态的能量差为,它是谐振子的能量量子, 称它为声子 ,正如人们把电磁辐射的能量量子称 为光子一样。 3NS个格波与3NS个量子谐振子一一对应,因此式 (3-57)也是一个频率为ω的格波的能量。频率 为ωi(q)的格波被激发的程度,用该格波所具有的 能量为ωi (q)的声子数n的多少来表征。
2.声子是一种准粒子
声子与声子,声子与其它粒子、准粒子互作用, 满足能量守恒。 不具有通常意义下的动量,常把q称为声子的
粒子数不守恒,例如温度升高后声子数增加。
准动量。
3.准动量选择定则
准动量的确定只能准确到可以附加任何 一个倒格矢Gh
ω(q)= ω(q+ Gh) Ex: 二声子作用 q1+q2=q3+Gh q1+q2=q3+Gh
系统的势能函数
系统的动能函数
系统的哈密顿量 H
1 1 V 2 i ( mi ) 0 i j 2 i 1 2 i , j 1 i j
3N 3N 2
—— 含有坐标的交叉项
§3-1 简谐近似和简正坐标 —— 晶格振动与晶体的热学性质
引入简正坐标
—— 原子的坐标和简正坐标通过正交变换联系起来 假设存在线性变换
1 能量本征值 i ( ni ) i 2
本征态函数
—— 谐振子方程
n (Qi ) iຫໍສະໝຸດ iexp(
2
2
) H ni ( )
— 厄密多项式
§3-1 简谐近似和简正坐标 ——
晶格振动与晶体的热学性质
简谐震动简正坐标(0301)

声学
在声学领域,声音的传播和辐射都 可以看作是简谐震动的叠加,因此 简谐震动理论也是声学研究的重要 基础。
02
简正坐标的概念
什么是简正坐标
• 简正坐标是一种描述系统振动的坐标方式,它将复 杂的振动问题简化为简单的数学模型,以便于分析 和求解。在简正坐标下,系统的振动形式被分解为 一系列正弦和余弦函数,每个函数代表一种独立的 振动模式。
简谐震动
简谐震动是物理学中一个基本而重要的概念,它描述的是一个振动系统在平衡 位置附近做周期性的往复运动。简谐震动可以用数学公式表示,其运动规律具 有特定的周期性和振幅。
简正坐标
简正坐标是用来描述简谐震动的坐标系,它能够将复杂的振动问题简化,方便 分析和计算。简正坐标系的选择取决于系统的具体形式和物理特性。
实例二:单摆的简谐震动
总结词
单摆在摆角较小的情况下,做近似于简谐振动的往复运动。
详细描述
单摆由一根长度为摆长的细线悬挂着一个质量块组成,在重 力作用下产生往复运动。当摆角较小(小于5度)时,单摆的 运动可以近似看作是简谐振动。在简正坐标系下,单摆的振 动形式可以表示为正弦或余弦函数。
实例三:电磁振荡器的简谐震动
教育教学
在高等教育中,简谐震动和简正坐标是物理学、工程学等专业的重要教学内容。通过深入 学习和理解简谐震动和简正坐标的理论基础,可以培养学生的逻辑思维和分析能力,提高 他们的科学素养。
THANKS
感谢观看
简正坐标的应用
1. 振动分析
简正坐标广泛应用于振动分析 领域,用于研究系统的振动特
性和响应。
2. 结构优化
在结构优化设计中,简正坐标 可以帮助分析结构的振动模态 和频率,从而优化结构的设计 。
3. 声学研究
在声学领域,声音的传播和辐射都 可以看作是简谐震动的叠加,因此 简谐震动理论也是声学研究的重要 基础。
02
简正坐标的概念
什么是简正坐标
• 简正坐标是一种描述系统振动的坐标方式,它将复 杂的振动问题简化为简单的数学模型,以便于分析 和求解。在简正坐标下,系统的振动形式被分解为 一系列正弦和余弦函数,每个函数代表一种独立的 振动模式。
简谐震动
简谐震动是物理学中一个基本而重要的概念,它描述的是一个振动系统在平衡 位置附近做周期性的往复运动。简谐震动可以用数学公式表示,其运动规律具 有特定的周期性和振幅。
简正坐标
简正坐标是用来描述简谐震动的坐标系,它能够将复杂的振动问题简化,方便 分析和计算。简正坐标系的选择取决于系统的具体形式和物理特性。
实例二:单摆的简谐震动
总结词
单摆在摆角较小的情况下,做近似于简谐振动的往复运动。
详细描述
单摆由一根长度为摆长的细线悬挂着一个质量块组成,在重 力作用下产生往复运动。当摆角较小(小于5度)时,单摆的 运动可以近似看作是简谐振动。在简正坐标系下,单摆的振 动形式可以表示为正弦或余弦函数。
实例三:电磁振荡器的简谐震动
教育教学
在高等教育中,简谐震动和简正坐标是物理学、工程学等专业的重要教学内容。通过深入 学习和理解简谐震动和简正坐标的理论基础,可以培养学生的逻辑思维和分析能力,提高 他们的科学素养。
THANKS
感谢观看
简正坐标的应用
1. 振动分析
简正坐标广泛应用于振动分析 领域,用于研究系统的振动特
性和响应。
2. 结构优化
在结构优化设计中,简正坐标 可以帮助分析结构的振动模态 和频率,从而优化结构的设计 。
3. 声学研究
固体物理总复习

gap
2 )q 一维双原子链的长声学波 ( a mM B 长声学波中相邻原子的振动 ( A ) 1
光学波 长波极限
2
mM B m , ( ) - mM A M
§3.4
1. 三维复式格子
三维晶格的振动
l i [ t R l k q ] 格波的一般形式 A e k k
ab c
§5 晶体的宏观对称性
点对称操作 1. 绕轴旋转 2.旋转-反演(反演,镜面) 对称操作
1. 绕轴旋转
2.旋转-反演 3.空间平移
晶体的宏观对称性只有8种独立的对称操作: 1,2,3,4,6, 1 ( i ),
2 (m)
和
4
能证明为何晶体中没有5次对称性?
第二章
• 晶体结合的类型? • 晶体结合的物理本质? • 固体结合的类型与固体性质之间的联系?
T —— 电子对比热的贡献, 即电子热容
AT 3—— 晶格振动对比热的贡献, 即晶格热容
温度不太低时,可以忽略电子的贡献 爱因斯坦模型与德拜模型 爱因斯坦温度和德拜温度
§3.9 晶格振动模式密度
晶格振动模式密度 —— 单位频率间隔的振动模式数目
n g ( ) lim 0
在q空间,晶格振动模是均匀分布的,状态密度
本课程的主要内容
晶格动力学
原子核的运动规律 核外电子的运动规律
固体物理
固体电子论
晶格动力学
1. 晶体结构 2. 固体的结合 3. 晶格振动和热学性质
固体电子论
4. 能带理论 5. 外场中电子的运动 6. 金属电子论
第一章 摘
§1-1 §1-2 §1-3 §1-4 §1-5 §1-6 §1-7 §1-8 §1-9
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
简正振动 —— 所有原子参与的振动,振动频率相同 振动模 —— 简正坐标代表所有原子共同参与的一个振动
§3-1 简谐近似和简正坐标 —— 晶格振动与晶体的热学性质
只考察某一个振动模
系aij mi
Asin( jt )
正则动量算符
系统薛定谔方程
(1
§3-1 简谐近似和简正坐标 —— 晶格振动与晶体的热学性质
讨论 1.声子是玻色子
一个模式可以被多个相同的声子占据,ω 和q相同的声子不可区分,自旋为零。满足玻 色统计。
除碰撞外,不考虑它们之间的相互作用, 则可视为近独立子系,则玻色统计与玻尔兹 曼统计一致。
玻色子(boson),得名于印度物理学家玻色.。玻色 子是指自旋为整数的粒子。不遵守泡利不相容原理。 在低温时可以发生玻色-爱因斯坦凝聚。符合玻色- 爱因斯坦统计.
原子位移宗量
§3-1 简谐近似和简正坐标 —— 晶格振动与晶体的热学性质
N个原子的位移矢量 —— 体系的势能函数在平衡位置按泰勒级数展开
取
平衡位置
—— 不计高阶项
系统的势能函数
V
1 2
3N 2V (
i, j1 i j
)0 i j
§3-1 简谐近似和简正坐标 —— 晶格振动与晶体的热学性质
摩尔热容量 CV 3Nk 3R —— 与温度无关
—— 杜隆-珀替经验规律
—— 实验表明较低温度下,热容量随着温度的降低而下降 晶格振动 —— 研究固体宏观性质和微观过程的重要基础 晶格振动 —— 晶体的热学性质、电学性质、光学性质、超
导电性、磁性、结构相变有密切关系
§3-1 简谐近似和简正坐标 —— 晶格振动与晶体的热学性质
简写成:
三.平均声子数
各个格波可能具有不同的声子数, 在一定温度的热平衡态,一个格波的 平均声子数有多少呢?
由于声子间相互作用很弱,除了碰 撞外,可不考虑它们之间的相互作用, 故可把声子视为近独立子系,这时玻 色-爱因斯坦统计与经典的玻尔兹曼 统计是一致的。
n(,T )=
2.声子是一种准粒子
粒子数不守恒,例如温度升高后声子数增加。
声子与声子,声子与其它粒子、准粒子互作用,
满足能量守恒。 不具有通常意义下的动量,常把q称为声子的 准动量。
3.准动量选择定则
准动量的确定只能准确到可以附加任何 一个倒格矢Gh
ω(q)= ω(q+ Gh) Ex: 二声子作用 q1+q2=q3+Gh q1+q2=q3+Gh
2
3N i1
pi2
1 2
3N
i2Qi2 ) (Q1, Q3N )
i1
E (Q1,
Q3N )
§3-1 简谐近似和简正坐标 —— 晶格振动与晶体的热学性质
任意一个简正坐标 能量本征值
1 [2 2
2 Qi2
i2Qi2 ] (Qi )
i (Qi )
i
(ni
系统的势能函数
系统的动能函数
系统的哈密顿量
H
1 2
3N i1
mi i 2
1 2
3N 2V (
i, j1 i j
)0 i j
—— 含有坐标的交叉项
§3-1 简谐近似和简正坐标 —— 晶格振动与晶体的热学性质
引入简正坐标 —— 原子的坐标和简正坐标通过正交变换联系起来 假设存在线性变换
原子的振动 —— 晶格振动在晶体中形成了各种模式的波 —— 简谐近似下,系统哈密顿量是相互独立简谐振动哈密
顿量之和 —— 这些模式是相互独立的,模式所取的能量值是分立的 —— 用一系列独立的简谐振子来描述这些独立而又分立的
振 动模式 —— 这些谐振子的能量量子,称为声子 —— 晶格振动的总体可看作是声子的系综
第三章 晶格振动与晶体的热学性质
晶格振动的研究 —— 晶体的热学性质 固体热容量 —— 热运动是晶体宏观性质的表现
杜隆-珀替经验规律
—— 一摩尔固体有N个原子,有3N个振动自由度,按能 量均分定律,每个自由度平均热能为kT
总的内能 E 3NkT
摩尔热容量
CV
(
E T
)T
§3-1 简谐近似和简正坐标 —— 晶格振动与晶体的热学性质
i 1
ni (Qi )
i
exp(
2
2
)
H
ni
(
)
§3-1 简谐近似和简正坐标 —— 晶格振动与晶体的热学性质
二 、能量量子和声子 (量子力学修正)
把上述经典谐振子的能量用量子力 学的结果来表示。量子力学告诉我 们,频率为的谐振子,其能量为
En=
1 2
n
n=0,1,2…… (3-57)
§3-1 简谐近似和简正坐标 —— 晶格振动与晶体的热学性质
§3-1 简谐近似和简正坐标
一、晶格振动和谐振子
简谐近似 —— 只考虑最近邻原子之间的相互作用 研究对象 —— 由N个质量为m的原子组成的晶体
第n个原子的平衡位置
偏离平衡位置的位移矢量
原子的位置 Rn ' Rn n (t)
3个方向上的分量
(坐标变换)
系统的哈密顿量
拉格朗日函数
正则动量
§3-1 简谐近似和简正坐标 —— 晶格振动与晶体的热学性质
系统的哈密顿量
正则方程
pi
H Qi
正则动量
pi
L Q i
Qi
Qi i2Qi 0, i 1, 2, 3, 3N —— 3N个独立无关的方程 简正坐标方程解 Qi Asin(it )
这表明谐振子处于不连续的能量状态。
当n=0时,它处于基态,E0=12 ,称为零点能。
相邻状态的能量差为,它是谐振子的能量量子, 称它为声子,正如人们把电磁辐射的能量量子称 为光子一样。
3NS个格波与3NS个量子谐振子一一对应,因此式 (3-57)也是一个频率为ω的格波的能量。频率 为ωi(q)的格波被激发的程度,用该格波所具有的 能量为ωi (q)的声子数n的多少来表征。
1 2
)
i
—— 谐振子方程
本征态函数
ni (Qi )
i
exp(
2
2
)
H
ni
(
)
— 厄密多项式
§3-1 简谐近似和简正坐标 —— 晶格振动与晶体的热学性质
N个原子组成的晶体 系统薛定谔方程
系统能量本征值
E
3N
i
i 1
3N i 1
(ni
1 2
)i
3N
系统本征态函数 (Q1, Q2, Q3,Q3N ) ni (Qi )
§3-1 简谐近似和简正坐标 —— 晶格振动与晶体的热学性质
只考察某一个振动模
系aij mi
Asin( jt )
正则动量算符
系统薛定谔方程
(1
§3-1 简谐近似和简正坐标 —— 晶格振动与晶体的热学性质
讨论 1.声子是玻色子
一个模式可以被多个相同的声子占据,ω 和q相同的声子不可区分,自旋为零。满足玻 色统计。
除碰撞外,不考虑它们之间的相互作用, 则可视为近独立子系,则玻色统计与玻尔兹 曼统计一致。
玻色子(boson),得名于印度物理学家玻色.。玻色 子是指自旋为整数的粒子。不遵守泡利不相容原理。 在低温时可以发生玻色-爱因斯坦凝聚。符合玻色- 爱因斯坦统计.
原子位移宗量
§3-1 简谐近似和简正坐标 —— 晶格振动与晶体的热学性质
N个原子的位移矢量 —— 体系的势能函数在平衡位置按泰勒级数展开
取
平衡位置
—— 不计高阶项
系统的势能函数
V
1 2
3N 2V (
i, j1 i j
)0 i j
§3-1 简谐近似和简正坐标 —— 晶格振动与晶体的热学性质
摩尔热容量 CV 3Nk 3R —— 与温度无关
—— 杜隆-珀替经验规律
—— 实验表明较低温度下,热容量随着温度的降低而下降 晶格振动 —— 研究固体宏观性质和微观过程的重要基础 晶格振动 —— 晶体的热学性质、电学性质、光学性质、超
导电性、磁性、结构相变有密切关系
§3-1 简谐近似和简正坐标 —— 晶格振动与晶体的热学性质
简写成:
三.平均声子数
各个格波可能具有不同的声子数, 在一定温度的热平衡态,一个格波的 平均声子数有多少呢?
由于声子间相互作用很弱,除了碰 撞外,可不考虑它们之间的相互作用, 故可把声子视为近独立子系,这时玻 色-爱因斯坦统计与经典的玻尔兹曼 统计是一致的。
n(,T )=
2.声子是一种准粒子
粒子数不守恒,例如温度升高后声子数增加。
声子与声子,声子与其它粒子、准粒子互作用,
满足能量守恒。 不具有通常意义下的动量,常把q称为声子的 准动量。
3.准动量选择定则
准动量的确定只能准确到可以附加任何 一个倒格矢Gh
ω(q)= ω(q+ Gh) Ex: 二声子作用 q1+q2=q3+Gh q1+q2=q3+Gh
2
3N i1
pi2
1 2
3N
i2Qi2 ) (Q1, Q3N )
i1
E (Q1,
Q3N )
§3-1 简谐近似和简正坐标 —— 晶格振动与晶体的热学性质
任意一个简正坐标 能量本征值
1 [2 2
2 Qi2
i2Qi2 ] (Qi )
i (Qi )
i
(ni
系统的势能函数
系统的动能函数
系统的哈密顿量
H
1 2
3N i1
mi i 2
1 2
3N 2V (
i, j1 i j
)0 i j
—— 含有坐标的交叉项
§3-1 简谐近似和简正坐标 —— 晶格振动与晶体的热学性质
引入简正坐标 —— 原子的坐标和简正坐标通过正交变换联系起来 假设存在线性变换
原子的振动 —— 晶格振动在晶体中形成了各种模式的波 —— 简谐近似下,系统哈密顿量是相互独立简谐振动哈密
顿量之和 —— 这些模式是相互独立的,模式所取的能量值是分立的 —— 用一系列独立的简谐振子来描述这些独立而又分立的
振 动模式 —— 这些谐振子的能量量子,称为声子 —— 晶格振动的总体可看作是声子的系综
第三章 晶格振动与晶体的热学性质
晶格振动的研究 —— 晶体的热学性质 固体热容量 —— 热运动是晶体宏观性质的表现
杜隆-珀替经验规律
—— 一摩尔固体有N个原子,有3N个振动自由度,按能 量均分定律,每个自由度平均热能为kT
总的内能 E 3NkT
摩尔热容量
CV
(
E T
)T
§3-1 简谐近似和简正坐标 —— 晶格振动与晶体的热学性质
i 1
ni (Qi )
i
exp(
2
2
)
H
ni
(
)
§3-1 简谐近似和简正坐标 —— 晶格振动与晶体的热学性质
二 、能量量子和声子 (量子力学修正)
把上述经典谐振子的能量用量子力 学的结果来表示。量子力学告诉我 们,频率为的谐振子,其能量为
En=
1 2
n
n=0,1,2…… (3-57)
§3-1 简谐近似和简正坐标 —— 晶格振动与晶体的热学性质
§3-1 简谐近似和简正坐标
一、晶格振动和谐振子
简谐近似 —— 只考虑最近邻原子之间的相互作用 研究对象 —— 由N个质量为m的原子组成的晶体
第n个原子的平衡位置
偏离平衡位置的位移矢量
原子的位置 Rn ' Rn n (t)
3个方向上的分量
(坐标变换)
系统的哈密顿量
拉格朗日函数
正则动量
§3-1 简谐近似和简正坐标 —— 晶格振动与晶体的热学性质
系统的哈密顿量
正则方程
pi
H Qi
正则动量
pi
L Q i
Qi
Qi i2Qi 0, i 1, 2, 3, 3N —— 3N个独立无关的方程 简正坐标方程解 Qi Asin(it )
这表明谐振子处于不连续的能量状态。
当n=0时,它处于基态,E0=12 ,称为零点能。
相邻状态的能量差为,它是谐振子的能量量子, 称它为声子,正如人们把电磁辐射的能量量子称 为光子一样。
3NS个格波与3NS个量子谐振子一一对应,因此式 (3-57)也是一个频率为ω的格波的能量。频率 为ωi(q)的格波被激发的程度,用该格波所具有的 能量为ωi (q)的声子数n的多少来表征。
1 2
)
i
—— 谐振子方程
本征态函数
ni (Qi )
i
exp(
2
2
)
H
ni
(
)
— 厄密多项式
§3-1 简谐近似和简正坐标 —— 晶格振动与晶体的热学性质
N个原子组成的晶体 系统薛定谔方程
系统能量本征值
E
3N
i
i 1
3N i 1
(ni
1 2
)i
3N
系统本征态函数 (Q1, Q2, Q3,Q3N ) ni (Qi )
