九年级数学由三角函数值求角PPT教学课件
合集下载
沪科版初中数学九年级上册 特殊角的三角函数值 经典课件

归纳总结
当然如果记不住这些规律及特殊角的三角函数
值,也可以根据这两个含特殊角的三角形的三
边之比和三角函数的定义进行推导。
A
A
30
3
2
45
1
2
沪科版初中数学九年级上册 特殊角的三角函数值 经典课件
C
B
1
C
1
B
沪科版初中数学九年级上册 特殊角的三角函数值 经典课件
随堂练习
例1 计算: (1)2sin60°+3tan30 °+tan45°;
(2)当 090 时, α的余弦值随着角度的增大而减小, 随着角度的减小而增大;
(3)当 090时,α的正切值随着角度的增大而增大, 随着角度的减小而减小;
沪科版初中数学九年级上册 特殊角的三角函数值 经典课件
沪科版初中数学九年级上册 特殊角的三角函数值 经典课件 沪科版初中数学九年级上册 特殊角的三角函数值 经典课件
归纳总结
从表中可发现下列规律:(1)当a= 30°、 45°、60°时, sin a的分子的被开方数依 次为1,2,3,逐渐增大, sin a的分母都是2。
(2)cos a的分子的被开方数依次为3,2,1,逐
渐减小, cos a的分母都是2。
(3) sin 30°= cos 60°= 1
sin 45°= cos 45°= 2 2
2
sin 60°= cos 30°=
3
2
沪科版初中数学九年级上册 特殊角的三角函数值 经典课件
沪科版初中数学九年级上册 特殊角的三角函数值 经典课件
(4)当a= 30°、45°、60°时, tan a的值从
31
3
3 逐渐增大。
新华师大版九年级数学上册《特殊角的三角函数值》课件

解:如图,根据题意可知,
∠AOD 1600 300, OD=2.5m, 老师提示: B
2
将实际问题
cos300 OC,
数学化.
OD
O C OcD o 30 s0 2.532.16 (m )5.
2
∴AC=2.5-2.165≈0.34(m).
∴最高位置与最低位置的高度差约为0.34m.
O
●
2.5
┌C D A
(6)tan45°,tan60°等于多少?
请与同伴交流,完成右表:
45° ┌ 60° ┌
三角 函数
锐角α
正弦 sinα
余弦 cosα
正切 tanα
30° 45° 60°
要能记 住有多好
特殊角的三角函数值表
驶向胜利 的彼岸
三角函数
锐角α
正弦sinα 余弦cosα
正切 tanα
30°
1 2
3 2
3 3
2
(5)在Rt⊿ABC中, ∠C=90°,若∠B= 2∠A,则tanA= 3 3
60° 90°
真知在实践中诞生
驶向胜利 的彼岸
例 一个小孩荡秋千,秋千链子的长度为2.5m, 当秋千向两边摆动时,摆角恰好为600,且两边摆
动的角度相同,求它摆至最高位置时与其摆至最
低位置时的高度之差(结果精确到0.01m).3 2来自21 22
1
sin260°表示 (sin60°)2,
cos260°表示
31
(cos60°)2,
1 44
其余类推.
0.
例题
驶向胜利 的彼岸
求值:sin30°×tan30°+cos60°×tan60°
解:sin30°×tan30°+cos60°×tan60°
23.一般锐角的三角函数值PPT课件(沪科版)

解:(1)过点C作CD⊥AB于点D, ∵AC=10千米,∠CAB=25°, ∴CD=sin∠CAB·AC=sin25°×10≈0.42×10=4.2(千米), AD=cos∠CAB·AC=cos25°×10≈0.91×10=9.1(千米). ∵∠CBA=45°,∴BD=CD=4.2(千米),
B C = C D 4 .2 5 .9 (千 米 ), sin C BA sin 45
【方法总结】解决问题的关键是作出辅助线,构造直 角三角形,利用三角函数关系求出有关线段的长.
例4:如图,课外数学小组要测量小山坡上塔的高度 DE,DE所在直线与水平线AN垂直.他们在A处测得塔 尖D的仰角为45°,再沿着射线AN方向前进50米到达B 处,此时测得塔尖D的仰角∠DBN=61.4°,小山坡坡 顶E的仰角∠EBN=25.6°.现在请你帮助课外活动小组 算一算塔高DE大约是多少米 (结果精确到个位).
解:延长DE交AB延长线于点F,则∠DFA=90°.
∵∠A=45°,
∴AF=DF.
设EF=x,
∵tan25.6°= EF ≈0.5,
BF
∴BF=2x,则DF=AF=50+2x,
故tan61.4°=
DF BF
50 2x 2x
=1.8,
解得x≈31.
故DE=DF-EF=50+31×2-31=81(米).
所以,塔高DE大约是81米.
归纳总结
解决此类问题要了解角之间的关系,找到 与已知和未知相关联的直角三角形,当图形中 没有直角三角形时,要通过作高或垂线构造直 角三角形.
巩固练习
1. 已知下列锐角三角函数值,用计算器求其相应 的锐角: (1)sinA=0.627 5,sinB=0.054 7;
∠A=38°51′57″ ∠B=38°8″
B C = C D 4 .2 5 .9 (千 米 ), sin C BA sin 45
【方法总结】解决问题的关键是作出辅助线,构造直 角三角形,利用三角函数关系求出有关线段的长.
例4:如图,课外数学小组要测量小山坡上塔的高度 DE,DE所在直线与水平线AN垂直.他们在A处测得塔 尖D的仰角为45°,再沿着射线AN方向前进50米到达B 处,此时测得塔尖D的仰角∠DBN=61.4°,小山坡坡 顶E的仰角∠EBN=25.6°.现在请你帮助课外活动小组 算一算塔高DE大约是多少米 (结果精确到个位).
解:延长DE交AB延长线于点F,则∠DFA=90°.
∵∠A=45°,
∴AF=DF.
设EF=x,
∵tan25.6°= EF ≈0.5,
BF
∴BF=2x,则DF=AF=50+2x,
故tan61.4°=
DF BF
50 2x 2x
=1.8,
解得x≈31.
故DE=DF-EF=50+31×2-31=81(米).
所以,塔高DE大约是81米.
归纳总结
解决此类问题要了解角之间的关系,找到 与已知和未知相关联的直角三角形,当图形中 没有直角三角形时,要通过作高或垂线构造直 角三角形.
巩固练习
1. 已知下列锐角三角函数值,用计算器求其相应 的锐角: (1)sinA=0.627 5,sinB=0.054 7;
∠A=38°51′57″ ∠B=38°8″
新北师大版九年级数学下册《三角函数的计算》优质ppt教学课件
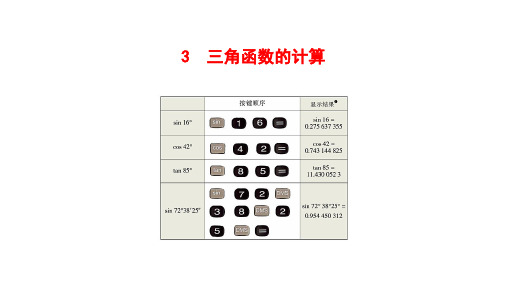
上表的显示结果是以“度”为单位的,再按 ˚ ′ ″ 键即可显示 以“度、分、秒”为单位的结果.
根据上述方法你能求出问题1中∠A的大小吗?
sin A = 1 = 0.25. 按键顺序和显示结果为
4
SHIFT sin 0 · 2 5 = 14.477 512 19°
再按 ° ′ ″ 键可显示14˚28′39″,所以∠A=14˚28′39″.
正弦值随着角度的增大(或减小)而增大(或减小); 余弦值随着角度的增大(或减小)而减小(或增大); 正切值随着角度的增大(或减小)而增大(或减小).
知识点1 利用计算器求锐角三角函数值
1.如图,在△ABC中,∠ACB=90°,∠ABC=26°,BC=5.若用科学计算器 求边AC的长,则下列按键顺序正确的是( D )
D 39°
E
45°
C
A
【解析】(1)由题意,AC=AB=610 米.
(2)DE=AC=610米,
在Rt△BDE中,tan∠BDE= BE ,
DE
故BE=DEtan39°. 因为CD=AE,
所以CD=AB-DE·tan 39°
=610-610×tan 39°≈116(米). 答:大楼的高度CD约为116 米.
B.sin65°54′-sin35°54′=sin30°
C.2sin15°30′=sin31°
D.sin72°18′-sin12°18′=sin47°42′
•2. 已知sin α=1 ,求α,若用科学计算器计算且结果以“度、分、秒
2
”为单位,最后按键(D )
•A.AC/ON
B. SHIFT
C.MODE
(4)sin18°+cos55°-tan59°≈-0.7817.
沪科版九年级数学上册2锐角的三角函数(第3课时特殊角的三角函数值)课件

B
2a
a
45.0
A
C
a
Sin45°=
A 的 对 边 斜边
2 2
cos45°=
A的邻边 2
斜边
2
tan45°=
A的对边 1 A 的邻边
归纳
特殊角的三角函数值
30o
45o
sinα
1 2
2 2
cosα
3 2
2 2
3
tanα
3
1
60o
3 2
1 2
3
讨论:
30o
45o
sinα
1 2
2 2
cosα
3
2
公式一
2、三角公式
当∠A+∠B=90°时
B
c
a
┌
A
b
C
sinA=cosB cosA=sinB
tanA . tanB=1
公式二
sin2 A cos2 A 1 tan A sin A cos A
新知探究
已知Rt△ABC中,∠A=30°
B
a
2a
Sin30°=
A的对边 1
斜边
2
C
30.0 A
3a
60o
3 2
1 2
3
角度逐 渐增大
正切值 也增大
讨论: 锐角A的正弦值、余弦值有无变化范围?
30o
1
sinα 2
cosα 3 2 3
tanα 3
45o
2 2
2 2
1
60o
3 2
1 2
3
0< sinA<1 0<cosA<1
归纳
冀教版九年级数学上册《锐角三角函数的计算》PPT精品课件

9
8
1
观察计算的结果,当α增大时,角α的正弦值、余弦值、正切值怎样变化?
正弦值随着角度的增大(或减ቤተ መጻሕፍቲ ባይዱ)而增大(或减小)
余弦值随着角度的增大(或减小)而减小(或增大) 正切值随着角度的增大(或减小)而增大(或减小)
知识讲解
2.已知一个锐角三角函数的值求锐角的度数
例2 用计算器求下列各锐角的度数:(结果精确到1″) (1)已知cosα=0.5237,求锐角α; (2)已知tanβ=1.6480,求锐角β.
知识讲解
(2)在计算器开机状态下,按键顺序为
2ndF tan-1 1 . 6 4 显示结果为58.750 786 43. 即β≈58.750 786 43°.
80=
再继续按键: 2ndF
DEG
显示结果为58□45□2.83.
即β≈58°45‘ 3″.
知识讲解
例3 如图所示,在Rt△ABC中,∠C=90°,AB=5,BC=4.
2.已知 sin232°+cos2α=1,则锐角α等于( A )
A.32°
B.58°
C.68°
D.以上结论都不对
3.用计算器验证,下列各式中正确的是( D ) A.sin18°24′+sin35°26′=sin45° B.sin65°54′-sin35°54′=sin30° C.2sin15°30′=sin31° D.sin72°18′-sin12°18′=sin47°42′
2.求cos72°的值. 第一步:按计算器 cos 键,
第二步:输入角度值72, 第三步:输入 键, 屏幕显示结果为0.309 016 994.
即cos 72°=0.309 016 994.
人教版九年级数学下册三角函数全章课件

B.
C.
D.
【解析】选B.根据正切的函数定义,角A的正切应是它的 对边与邻边的比,所以B是正确,A是∠B的正切;C和D都 错.
2.(黄冈中考)在△ABC中,∠C=90°,sinA= 则tanB=( B )
3.(丹东中考)如图,小颖利用有一
C
个锐角是30°的三角板测量一棵树的高度, 30
已知她与树之间的水平距离BE为5m,AB为 °A
【规律方法】 1.记住30°,45 °,60 °的特殊值,及推导方式,可以 提高计算速度. 2.会构造直角三角形,充分利用勾股定理的有关知识结 合三角函数灵活运用.
B
直角三角形三边的关系.
直角三角形两锐角的关系. A
直角三角形边与角之间的关系.
c
a
┌
b
C
特殊角30°,45°,60°角的三角函数值. 30° 互余两角之间的三角函数关系.
2)如图,sinA=
(×)
2.在Rt△ABC中,锐角A的对边和斜边同时扩大100倍,sinA
的值( C )
A.扩大100倍 C.不变
B.缩小 1
100
D.不能确定
3.如图 A
B
1
3
,则 sinA=___2___ .
30°
C
7
1.(温州中考)如图,在△ABC中,∠C=90°, AB=13,
BC=5,则sinA的值是(
)
A. 5 13
B. 12
13
C. 5
12
D. 13
5
【解析】选A.由正弦的定义可得
sin A BC 5 . AB 13
2.在平面直角平面坐标系中,已知点A(3,0)和B(0,-4),则
已知三角函数值求角优质课件PPT

y=cosx 在________________________上是减函数,在
____________________________上是增函数 .正切函数 y=tanx 在___(_-_π_2_+__kπ_,__π2_+__k_π_)_(_k∈__Z_)___上是增函数.
我们知道,任意给定一个角,只要这 个角的三角函数值存在,就可以求出这 个三角函数值;反过来,已知一个三角 函数值,也可以求出与它对应的角。
求x的取值集合.
{61 ,299 }
例3. 已知tanx=
3 3
,且x∈(
2
,
2
)
,求x的值.
解:因为正切函数在(
2
,
2
)
上是增函数,
所以正切值等于
3 3
的角x有且只有1个.
由tan( )=-tan
6
6
=-
3 3
,
所以x=-
6
已知三角函数值求角
(3)已知 cos x 0.4665 ,
22
例2. 已知cosx=0.5,
(1)若 [0, ] ,求x;
(2)若 x [0, 2 ),求x;
(3)若 x∈R,求x的取值集合。 解:(1)由于cosx=0.5,所以x是第一或第四 象限的角. 因为cos =0.5,所以符合条件在第一象限的
3
角x= .
3
由诱导公式知cos(2π-x)=cosx,
62
22
6
(2) 若 x [0, 2 ) ,求x;
解得x1=
6
,x2=
5 6
.
(3)若 x∈R,求x的取值集合。
比较(1),(2)得x的取值集合是
{x | x 2k , k Z} {x | x 2k 5 , k Z}
____________________________上是增函数 .正切函数 y=tanx 在___(_-_π_2_+__kπ_,__π2_+__k_π_)_(_k∈__Z_)___上是增函数.
我们知道,任意给定一个角,只要这 个角的三角函数值存在,就可以求出这 个三角函数值;反过来,已知一个三角 函数值,也可以求出与它对应的角。
求x的取值集合.
{61 ,299 }
例3. 已知tanx=
3 3
,且x∈(
2
,
2
)
,求x的值.
解:因为正切函数在(
2
,
2
)
上是增函数,
所以正切值等于
3 3
的角x有且只有1个.
由tan( )=-tan
6
6
=-
3 3
,
所以x=-
6
已知三角函数值求角
(3)已知 cos x 0.4665 ,
22
例2. 已知cosx=0.5,
(1)若 [0, ] ,求x;
(2)若 x [0, 2 ),求x;
(3)若 x∈R,求x的取值集合。 解:(1)由于cosx=0.5,所以x是第一或第四 象限的角. 因为cos =0.5,所以符合条件在第一象限的
3
角x= .
3
由诱导公式知cos(2π-x)=cosx,
62
22
6
(2) 若 x [0, 2 ) ,求x;
解得x1=
6
,x2=
5 6
.
(3)若 x∈R,求x的取值集合。
比较(1),(2)得x的取值集合是
{x | x 2k , k Z} {x | x 2k 5 , k Z}
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
老师期望: 你能独立获得成功.
小结 拓展
回味无穷
由锐角的三角函数值反求锐角
驶向胜利 的彼岸
填表:已知一个角的三角函数值,求这个角的度数(逆向思维)
sin A 1 2
∠A= 300 sinA 3
2
∠A=
600 sinA 2 ∠A= 450
2
cosA 1 2
∠A= 600 cosA 2 ∠A=
2
450 cosA 3 ∠A=
c
c
互余两角之间的三角函数关系:
sinA=cosB.
同角之间的三角函数关系:
sin2A+cos2A=1. tanAsinA.
A
coAs
B
c
a
┌
b
C
特殊角300,450,600角的三角函数值.
想一想P17 2
数学源于生活的需求
如图,为了方便行人,市政府在10m 高的天桥.两端修建了40m长的斜道. 这条斜道的倾斜角是多少? 如图,在Rt△ABC中,
老师期望: 先将实际问题数学化,然后运用所学 知识予以解答.
随堂练习P270
真知在实践中诞生
驶向胜利 的彼岸
咋办
?
3. 图中的螺旋形由一系列直角 三角形组成.每个三角形都以点O
为一顶点.
(1)求∠A0OA1,∠A1OA2,∠A2OA3, 的大小.
(2)已知∠An-1OAn,是一个小于200 的角,求n的值.
行家看“门道”
驶向胜利 的彼岸
例2 如图,一名患者体内某重要器官后面有一肿瘤.在
接受放射性治疗时,为了最大限度地保证疗效,并且防
止伤害器官,射线必需从侧面照射肿瘤.已知肿瘤在皮
下6.3cm的A处,射线从肿瘤右侧9.8cm的B处进入身体,
求射线的入射角度.
?怎样
解答
解:如图,在Rt△ABC 中,AC=6.3cm,BC=9.8cm,
tan-1=56.78 =88.991 020 49
由于计算器的型号与功能的不同,按相应的说明书使用.
随堂练习P240
熟能生巧
驶向胜利 的彼岸
1 根据下列条件求∠θ的大小: (1)tanθ=2.988 8;(2)sinθ=0.395 7; (3)cosθ=0.785 0;(4)tanθ=0.897 2.
2
300
tanA 3 ∠A=
3
300 tanA 3 ∠A= 600
taA n1∠A= 450
独立
作业
知识的升华
P20 习题1.5 1,2,3题;
祝你成功!
驶向胜利 的彼岸
怎 么解?
老师提示:上表的显示结果是以度为 单位的,再按 dms 键即可显示以 “度,分,秒”为单位的结果.
例题欣赏P159
洞察力与内秀
驶向胜利 的彼岸
例1 如图,工件上有一V型槽,测得它的上口宽20mm,深19. 2mm.求V型角(∠ACB)的大小(结果精确到10 ).
解 : taA nC A D D 10 0 .52 , 08 CD 1.2 9
咋
∴∠ACD≈27.50 .
办
∴∠ACB=2∠ACD≈2×27.50 =550.
数
∴V型角的大小约550.
学化
呀!
随堂练习P270
真知在实践中诞生
驶向胜利 的彼岸
2 一辆汽车沿着一山坡行驶了1000m,其铅直高度 上升了50m.求山坡与水平面所成的锐角的大小.
咋办
?
老师期望: 你具有成功的把握.
例题欣赏P159
九年级数学(下)第一章 直角三角形的边角关系
3.三角函数的有关计算 (2)由三角函数值求角的度数
回顾与思考1
直角三角形的边角关系
驶向胜利 的彼岸
直角三角形三边的关系: 勾股定理 a2+b2=c2.
直角三角形两锐角的关系:两锐角互余 ∠A+ ∠B=900.
直角三角形边与角之间的关系:锐角三角函数
siA ncoBsa,coAssiB nb,
CosA=0.8607 2ndf cos 0 . 8 6 0 7 =
tanA=0.1890 2ndf tan 0 . 1 8 9 0 =
tanA=56.78 2ndf tan 5 6 . 7 8 =
tan 键的第二
显示结果
Sin-1=0.9816 =78.991 840 39 coS-1=0.8607 =30.604 730 07 tan-1=0.189 0 =10.702 657 49
siA nBC 10 1. AC404
那么∠A是多 少度呢? 要解决这问题,我们可以借助科学计算器.
请与同伴交流你是怎么做的?
做一做P18 3
知识在于积累
驶向胜利 的彼岸
已知三角函数值求角度,要用到 sin cos 功能 Sin-1 cos-1 tan-1 和 2ndf 键 .
例如,
按键的顺序
SinA=0.9816 2ndf Sin 0 . 9 8 1 6 =
taB nAC 6.30.64.29 BC9.8
∴∠B≈320 44′13″.
因此,射线的入射角度约为320 44′13″.
随堂练习P260
知识的运用
驶向胜利 的彼岸
1. 已知sinθ=0.82904,求∠θ,已知梯子长 4m,梯子位于地面上的一端离墙壁2.5m, 求梯子与地面所成的锐角.
