能量均分定理麦克斯韦速率分布.ppt
合集下载
经典:第四讲-速度分布函数-麦克斯韦速率

速率v的函数,称为速率分布函数。
f (v) dN Ndv
速率分布函数
理解分布函数的几个要点:
1.条件:一定温度(平衡态)和确定的气体系统,T和m是一定的; 2.范围:(速率v附近的)单位速率间隔,所以要除以dv;
3.数学形式:(分子数的)比例,局域分子数与总分子数之比。
8
物理意义:
速率在 v 附近,单位速率区间的分子数占总分子数
• dN/N 是 v 的函数; •当速率区间足够小时(宏观小,微观大), dN/N还应与
区间大小成正比。
为此,规定以单位速率间隔为比较标准,即 dN ,这样,比
Ndv
值 dN
Ndv
就反映出了分布随速率v的改变而改变。为此我们规定;
7
定义:处于一定温度下的气体,分布在速率v附近的
单位速率间隔内的分子数占总分子数的百分比只是
(2) 氢气在该温度时的最概然速率和方均根速率
解 (2)
vp
2RT
M
RT 2 103
1000
m/s
RT
f(v)
(v p )H2 103
1.41 103 m/s
( v 2 )H2
3RT M
1.73103 m/s
He H2
1000
v
29
例2 有N 个粒子,其速率分布函数为
f (v )
(2) 因为速率分布曲线下的面积代表一定速率区间内 的分子与总分子数的比率,所以
v v0 的分子数与总分子数的比率为
N
N
v0a
v0
2 3v 0
2 3
N 2 N
3
因此, v>v0 的分子数为 ( 2N/3 ) f (v )
f (v) dN Ndv
速率分布函数
理解分布函数的几个要点:
1.条件:一定温度(平衡态)和确定的气体系统,T和m是一定的; 2.范围:(速率v附近的)单位速率间隔,所以要除以dv;
3.数学形式:(分子数的)比例,局域分子数与总分子数之比。
8
物理意义:
速率在 v 附近,单位速率区间的分子数占总分子数
• dN/N 是 v 的函数; •当速率区间足够小时(宏观小,微观大), dN/N还应与
区间大小成正比。
为此,规定以单位速率间隔为比较标准,即 dN ,这样,比
Ndv
值 dN
Ndv
就反映出了分布随速率v的改变而改变。为此我们规定;
7
定义:处于一定温度下的气体,分布在速率v附近的
单位速率间隔内的分子数占总分子数的百分比只是
(2) 氢气在该温度时的最概然速率和方均根速率
解 (2)
vp
2RT
M
RT 2 103
1000
m/s
RT
f(v)
(v p )H2 103
1.41 103 m/s
( v 2 )H2
3RT M
1.73103 m/s
He H2
1000
v
29
例2 有N 个粒子,其速率分布函数为
f (v )
(2) 因为速率分布曲线下的面积代表一定速率区间内 的分子与总分子数的比率,所以
v v0 的分子数与总分子数的比率为
N
N
v0a
v0
2 3v 0
2 3
N 2 N
3
因此, v>v0 的分子数为 ( 2N/3 ) f (v )
第四、五讲 麦克斯韦分布律 能均分定理

N 0 dvx dvy dvznvx f (vx , vy , vz )dt dA
n
0
vx
f
(vx
)dvxdAdt
kT
2 m
1/
2
dAdt
1 nv dAdt
4
单位时间内与单位面积相碰的分子数 为
N 1 nv dtdA 4
v 为平均速率
§4.7 能量按自由度均分定理
§4.5 麦克斯韦分布律
大量分子整体在一定的条件下,它们的速度的分布却遵 从一定的统计规律,这个规律叫麦克斯韦速度分布律。若不考 虑分子速度的方向,则叫麦克斯韦速率分布律。
一、麦克斯韦按速度分布律
设气体总分子数为N,处于温度为T的平衡态时,
速度介于 vx vx dvx , vy vy dvy , vz vz dvz
质量为M的理想气体的内能为
M1
U
(t r 2s)RT
M 2
温度改变,内能改变量为
U M 1 (t r 2s)RT M 2
对于理想气体,等体过程 đQ dU
摩尔等体热容量为
CV ,
(
đQ dT
)V
dU dT
1 (t r 2
2s)R
例如:对于双原子分子气体, t r 2s 7
7 CV , 2 R
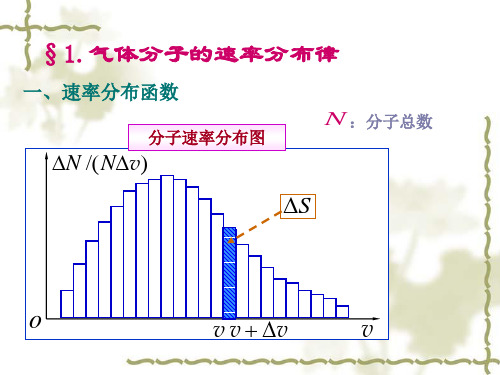
在v1—v2区间
dN f (v)dv N
N v2 f (v)dv
N
v1
f (v)
在0—区间有
dS
dN N
=面积
N 面积 N
f (v)dv 1
v 0 ——归一化条件 O v v dv v1 v2
三种统计速率
(1)最概然速率 vp 与f(v)极大值对应的速率。
能量均分

注意:对应分子的一个振动 自由度,除有一份 振动的动能外,还有一份平均势能 分子的平均能量
___
1 1 ( t r )kT kT 2 2
1 ( t r 2 )kT 2
令:i t r 2v
i kT 2
例:双原子(刚): t 3, r 2, i 5 : 5 kT
mv 2 2kT
v 2 dv
f (v )dv
1 dN f ( v) N dv
在温度为 T 的平衡状态下, 速率在 v 附近单位速率区间 的分子数占总数的比率 . 分子速率处在v附近单位速率区间中的几率(几率密度) 物理意义
1 dN f ( v) N dv
速率分布曲线
1 、分布函数总特征‘两头小, 中间大’(如图) 2 、a)速率在 v v dv 区间的分 子数占总分子数的百分比
结论:理想气体内能是温度的单值函数: E=E(T) (含义)
例:指出下列各式所表示的物理意义
1 3 i i m i (1) kT; ( 2) kT; ( 3) kT; (4) RT; (5) RT 2 2 2 2 M2
解(1)表示理想气体分子每一自由度 所具有的平均 能量 (2)表示单原子分子的平均动能或分子的平均平动 动能。 (3)表示自由度为i的分子的平均能量.
2
注意:
1)定理是一条统计规律,只能适用于大量分子的平 均或一个分子长时间的平均 2)能量均分到各自由度的原因 3)定理适用于液体和固体
二、理想气体内能 理想气体的内能 :分子动能和分子内原子间的 势能之和 . 平动
动 能 转 动 振动 势能(原子之间)
气体内能:气体包含的所有分子的动能,势能和分子间的相互作 用势能
第三章气体分子速率及能量分布ppt课件
麦克斯韦主要从事电磁理论、分子物理学、统计物理学、光学、力学、 弹性理论方面的研究。尤其是他建立的电磁场理论,将电学、磁学、光学统 一起来,是19世纪物理学发展的最光辉的成果,是科学史上最伟大的综合 之一。
麦克斯韦大约于1855年开始研究电磁学,在潜心研究了法拉第关于电 磁学方面的新理论和思想之后,坚信法拉第的新理论包含着真理。于是他抱 着给法拉第的理论“提供数学方法基础”的愿望,决心把法拉第的天才思想 以清晰准确的数学形式表示出来。他在前人成就的基础上,对整个电磁现象 作了系统、全面的研究,凭借他高深的数学造诣和丰富的想象力接连发表了 电磁场理论的三篇论文:《论法拉第的力线》(1855年12 月至1856年2 月);《论物理的力线》(1861至1862年);《电磁场的动力学理论》 (1864年12月8日)。对前人和他自己的工作进行了综合概括,将电磁场 理论用简洁、对称、完美数学形式表示出来,经后人整理和改写,成为经典 电动力学主要基础的麦克斯韦方程组。据此,1865年他预言了电磁波的存 在,电磁波只可能是横波,并计算了电磁波的传播速度等于光速,同时得出 结论:光是电磁波的一种形式,揭示了光现象和电磁现象之间的联系。 1888年德国物理学家赫兹用实验验证了电磁波的存在。。
(
m
2 kT
)3/
2
em
(
v
2 x
v 2y
vz2
)
/
2kT
dvx dv y dvz
引用速度空间的概念,可以对这个定律得到更直 观的理解。
速度空间:以vx, vy, vz为轴的直角坐标系(或 以v、θ、φ为坐标的球坐标系)所确定的空间。
速率分布公式:
dN 4 ( m )3/ 2 emv2 / 2kTv2dv
大学物理第 12 章 第 3 次课 -- 能均分定理 内能 麦克斯韦分布

§12.5
能量均分定理 理想气体内能
一、分子的平均总动能
1. 分子的运动的形式 物体的运动形式有平动、转动和振动. 气体分子的运动也可以有平动、转动和振动. 视具体情况而定. 2. 单原子分子的平均动能 单原子分子的理想气体, 分子可以看成质点, 分子只有平动. 因此单原子分子只有平动动能.
kt m 2 kT
2kT 2 RT m M
(8)
10 /14
上海师范大学
§12.6 麦克斯韦气体分子速率分布律 2. 平均速率 根据平均值的数学定义, 平均速率为
dN 1 dN1 2 dN 2 n dN n 0 N N m 2 f ( ) Nd m 3 / 2 2 2 kT 0 ) e d f ( )d 4 ( 0 0 N 2kT m 2 m 3/ 2 4 ( ) 3e 2 kT d 0 2kT
(iii) 刚性双原子分子的总平均动能为
kt kr
1 1 1 1 1 2 2 2 2 mCx mCy mCz Jy J z2 2 2 2 2 2 上海师范大学
(6)
2 /14
§12.5
能量均分定理 理想气体内能
非刚性双原子分子
4. 非刚性双原子分子的平均动能 对于非刚性双原子分子, 两原子间的距离随时间变化. 因此, 非刚性双原子分子除了平动和转动外, 还有振动. 如右图所示, 双原子分子好像被一根弹簧相连.
(2) 太阳的内能
3 41 E N N kT 1.1916 10 57 1.5 1.38 10 23 1.159 10 7 2.8610 ( J ) 2
上海师范大学
7 /14
§12.6 麦克斯韦气体分子速率分布律 理想气体分子的方均根速率
能量均分定理 理想气体内能
一、分子的平均总动能
1. 分子的运动的形式 物体的运动形式有平动、转动和振动. 气体分子的运动也可以有平动、转动和振动. 视具体情况而定. 2. 单原子分子的平均动能 单原子分子的理想气体, 分子可以看成质点, 分子只有平动. 因此单原子分子只有平动动能.
kt m 2 kT
2kT 2 RT m M
(8)
10 /14
上海师范大学
§12.6 麦克斯韦气体分子速率分布律 2. 平均速率 根据平均值的数学定义, 平均速率为
dN 1 dN1 2 dN 2 n dN n 0 N N m 2 f ( ) Nd m 3 / 2 2 2 kT 0 ) e d f ( )d 4 ( 0 0 N 2kT m 2 m 3/ 2 4 ( ) 3e 2 kT d 0 2kT
(iii) 刚性双原子分子的总平均动能为
kt kr
1 1 1 1 1 2 2 2 2 mCx mCy mCz Jy J z2 2 2 2 2 2 上海师范大学
(6)
2 /14
§12.5
能量均分定理 理想气体内能
非刚性双原子分子
4. 非刚性双原子分子的平均动能 对于非刚性双原子分子, 两原子间的距离随时间变化. 因此, 非刚性双原子分子除了平动和转动外, 还有振动. 如右图所示, 双原子分子好像被一根弹簧相连.
(2) 太阳的内能
3 41 E N N kT 1.1916 10 57 1.5 1.38 10 23 1.159 10 7 2.8610 ( J ) 2
上海师范大学
7 /14
§12.6 麦克斯韦气体分子速率分布律 理想气体分子的方均根速率
高二物理竞赛麦克斯韦速率分布律的实验验证PPT(课件)

P = P0 e -Mgh /RT
1°C),等温线接近双曲线,实际根气体据的行压为与强理想变气体化的行测为接高近。度,实际温度也随高度变化,测大气温
度有一定的范围,是近似测量。
例如在登山运动和航空驾驶中,通过测出不同高度处压强 的变化,根据(3)式可以计算出测点的高度。
理想气体等温线的p-V 图是一条双曲线。真实气体(例如 CO2 气体)的等温线是什么样呢?
1、 麦克斯韦速率分布律的实验验证
随着真空技术的发展,二十世纪二十年代后,陆续有许多 实验成功地验证了麦克斯韦速率分布律。
称为玻耳兹曼因子(式中 E 为粒子总能量),是决定粒子数分布的要素。
随★着重真力空场技中术的的气发体展分,子二按十高世度纪分二布1十9年2代0后年,陆法续有国许多的实验物成功理地验学证了家麦克施斯韦特速率恩分布(律O。.Stern,1888──1969)最
★ 玻耳兹曼分布率
以理想气体在重力场中分子按状态区间的分布为例。分子
处在重力场中受重力作用,分子的空间分布是“下密上
疏”,请看示意图。设气体分子在 x ~ x + dx, y ~ y + dy,
z ~ z + dvzx和~ vx dvx vy ~,vy dvy vz ,~ vz dvz 的总能为:
区间
E
Ek
Ep
1 2mv2Fra bibliotekEp1 2
m(vx2
v
2 y
vz2 )
Ep
玻耳兹曼分布律给出在状态区间 dvxdvydvzdxdydz 内的分子数为:
dN Ce(Ek Ep )/kTdvxdvydvydxdydz (1)
重力场中分子的分布
式中C为与速度和位置均无关的比例常数,其值为
8-3能量均分定理_理想气体的内能_8-5麦克斯韦分布律_8.

速率分布函数: f (v) dN Ndv
f (v)dv dN N
【思考】
v2 v1
f (v)dv
的物理含义?
在速率v1~ v2区间内的分子数占分子总 数的百分比, 或在该区间的出现概率。
第8章 气体动理论
14
第88-5章 麦气克体斯韦动分理布论律
二、麦克斯韦速率分布律(1859)
温度为T的平衡态下,气体分子速率分布的
平动自由度 i=3
x 双原子分子
平动自由度 =3
转动自由度= 2
i 5
z
三原子分子
C(x, y,z)
y
平动自由度 =3
转动自由度 =3
i 6
x 第8章 气体动理论
6
8-第3 8章能量均气分体定动理理论理想气体的内能
二 能量均分定理(Equipartition theorem of energy )
N
N
Nv
Nv
O
f (v) dN Ndv
v
v
O
面积大小代表速率v 附近dv区间内的分子 数占总分子数的比率
O
vp
v
v
dN dv dN
Ndv
N
第8章 气体动理论
12
第88-5章 麦气克体斯韦动分理布论律
麦克斯韦速率分布曲线
f(v)
f(vp)
面积= dN N
N v2 f (v)dv
概率密度为
f (v)
f
(v)
4
m
2 kT
3/
2
v2
emv2
/
2kT
T, m
最概然速率:
f (v)dv dN N
【思考】
v2 v1
f (v)dv
的物理含义?
在速率v1~ v2区间内的分子数占分子总 数的百分比, 或在该区间的出现概率。
第8章 气体动理论
14
第88-5章 麦气克体斯韦动分理布论律
二、麦克斯韦速率分布律(1859)
温度为T的平衡态下,气体分子速率分布的
平动自由度 i=3
x 双原子分子
平动自由度 =3
转动自由度= 2
i 5
z
三原子分子
C(x, y,z)
y
平动自由度 =3
转动自由度 =3
i 6
x 第8章 气体动理论
6
8-第3 8章能量均气分体定动理理论理想气体的内能
二 能量均分定理(Equipartition theorem of energy )
N
N
Nv
Nv
O
f (v) dN Ndv
v
v
O
面积大小代表速率v 附近dv区间内的分子 数占总分子数的比率
O
vp
v
v
dN dv dN
Ndv
N
第8章 气体动理论
12
第88-5章 麦气克体斯韦动分理布论律
麦克斯韦速率分布曲线
f(v)
f(vp)
面积= dN N
N v2 f (v)dv
概率密度为
f (v)
f
(v)
4
m
2 kT
3/
2
v2
emv2
/
2kT
T, m
最概然速率:
11 能均分定理 麦克斯韦速率分布

习题集:426、33、36、37、39、 40、51
P.15/40
气体分子平均平动动能
1 2 2 2 2 1 2 v , vx v y vz v 2 3 3 2 vx 2 1 2 1 vi kT 3kT 2 2
2
3 kT 2
刚性双原子分子: 刚性多原子分子:
5 kT 2 6 kT 2
P.1/40
平均自由程
v Z 1 2 π d 2n
kT 2 πd2p
例: 求氢在标准状况下分 子的平均碰撞频率和平均 自由程. (设分子直径 d = 210-10 m)
Z
1 2.14 107 m 2 π d 2n
v
7.95 10 9 s 1
P.14/40
作业
第7章 气体动理论
麦克斯韦速率分布曲线:
或速率在 [v1, v2] 区间内的分子数 占总分子数的百分比.
O
v v+dv v1
v2
v
P.7/40
第7章 气体动理论
理论曲线分析: 1. 图中小矩形面积: f ( v)dv 平衡态下, 分子出现在 [v, v+dv] 速率区间内的概率. 或速率在 [v, v+dv] 区间内的 分子数占总分子数的百分比. 2. 图中斜线部分面积: v2 N f ( v)dv v1 N 平衡态下, 分子出现在 [v1, v2] 速率区间内的概率.
第7章 气体动理论
7.6.3 三个统计速率
3. 方均根速率
v
2
1. 最概然速率(最可几速率) d f ( v) 0 dv
vp 2kT
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
r 转动
0 2 2 3 3
v 振动
0 0 2 0 6
i总
3 5
7 6 12
能量均分定理是经典的Boltzman统计中一个重要定
理,只有对于满足经典极限条件的粒子系统才成立。
(在各个能级上的粒子数远小于该能级的简并量子态数) (高温,低密度)
五、能量均分定理
经典统计和量子统计的研究对象和研究方法相同:
S N N
o
v v v
v
④ 若改变气体种类或温度再做实验,分布情况会
有差异,但仍然具有上述特点。
六、麦克斯韦气体分子速率分布律
1. 气体分子速率分布的测定
(3)速率分布函数
五、能量均分定理
2. 能量(按自由度)均分定理
(1)分子平动动能按自由度分配
1 2
mvx
2
1 2
mv y 2
1 2
mvz
2
1 2
kT
对于刚性分子vk 0
(2)分子动能按自由度分配
k
1 (t
2
r
vk
)k
T
(3)分子能量按自由度分配——能量均分定理
能量自由度 i t r v
(1)能量均分定理采用理性气体模型,认为分子 为无相互作用的弹性质点; 而实际分子间有相互作用、分子有大小。
(2)能量均分定理以经典力学为基础建立,认为 原子、分子等微观粒子的能量可以连续变化; 而近代物理学表明:原子、分子等微观粒子的运动 遵循量子力学规律(能量不连续,只能取一些分立 的值)。
例 某种理想气体的定压摩尔热容量 Cpm 29.1J mol 1 K 1
缝
N1 , N2 , N3 , NNN
接抽气泵
显 示
屏
l
六、麦克斯韦气体分子速率分布律
1. 气体分子速率分布的测定
(2)实验结果 一定种类的气体在一定温度下,其分子按速率的 分布是确定的,其具有一些共同的特点:
① 相对分子数 N 与分子的速率v 以及所取速率间隔 v
的大小有关;N
(1)一般气体的内能:
所有分子无规则运动的能量+分子间势能
理想气体的内能: 所有分子无规则运动的能量
E i RT
2
(2)理想气体的摩尔热容 ——经典热容理论
CV, m1
dQV dT
1 dE dT
i R
2
Cp,m i 2
Cp,m CV,m R
i
2
R
2
CV,m i
② 速率特别大或者特别小的分子的相对分子数都很小,
而位于某一速率间隔中的相对分子数最大;
③ 速率间隔取得越大,则相对分子数越大。 用 N 来消除 v 的影响,表示在速率v 附近单位速率区间
Nv 内的相对分子数。
六、麦克斯韦气体分子速率分布律
1. 气体分子速率分布的测定
(2)实验结果
N /(Nv)
仅取决于分子的自由度, 与气体种类、温度无关!
五、能量均分定理
(3)理论值与实验值的比较
自由度相同的气体, 热容并不相同;
单原子分子气体的热 容实验、理论值相符;
气体的热容与温度有关;
五、能量均分定理
(3)理论值与实验值的比较
多原子分子气体的热容 随温度呈阶梯状增长;
五、能量均分定理
思考:经典热容理论存在哪些缺陷?
量子统计 以量子力学为基础,粒子运动状态不连续;
粒子全同不可分辨,交换后状态不变! 例如:玻色分布(光子、介子等玻色子的最概然分布)、费米分 布(电子、质子等费米子的最概然分布)。 详见《基础物理学教程》(第二版) ,陆果,高等教育出版社,655-657
五、能量均分定理
3. 理想气体的内能和摩尔热容
Law of Maxwell Speed Distribution of Gas Molecules
1. 气体分子速率分布的测定
(1)实验装置及原理
2
l v
,
vl
1, 2, 3,
Hg
v1 v, v2 v, v3 v,金属蒸气 狭
d1, d2, d3,
(1)
Ekt
3 2
06 J
(2) E 5 V RT 4.16104 J
2M
2. 处于平衡态的气体分子具有确定的速
度平方平均值( v2 3kT
),反
m
映了大量分子无规则运动的统计规律性。
气体分子的速度遵循怎样的分布规律?
六、麦克斯韦气体分子速率分布律
都根据对物质微观结构和相互作用的认识,用概率统计的 方法,为由大量粒子组成的系统的宏观物理性质及其所遵 循的宏观规律提供微观解释,并揭示由大量微观粒子组成
的系统所固有的统计规律性。 不同点:
经典统计 以经典力学为基础,粒子运动状态具有连续性;
粒子全同可分辨,交换后状态变化; 例如:玻尔兹曼分布(如气体分子的最概然分布)。
求该气体分子在T=273K时的平均转动动能
i5 r 2
kt
2 2
kT
3.77 1021
J
例 闭合容器(V 5 3 3m,3 T=293K)内有空气
(视为理想气体)空气的M= 29103 kg mol 1,密度 1.29kg m 3
求:(1) 空气的平均平动动能总和; (2) 如果温度升高1.0K,则气体内能变化多大?
NO. 12-2
2011-12-2
一、能量均分定理
二、理想气体的内能及摩尔热容
三、麦克斯韦气体分子速率分布律 及 三个统计速率
四、分子平均自由程 及 平均碰撞频率
1.对于双原子分子或多原子分子,
分子有一定的内部结构,除平动外还有
分子的转动和分子内原子间的相对运动,
分子的平均动能和温度关系 是否仍然成立?
k
3 kT 2
五、能量均分定理
1. 空间自由度 决定物体的空间位置至少需要的独立坐标的数目。
刚体的一般运动包括: 刚体质心的平动和绕质心的转动。
要确定刚体在空间的位置,需要确定: ①质心的位置(x,y,z); ②刚体绕过质心的转轴的方位(θ,φ); ③刚体转轴从起始位置转过的角度ψ。
自由刚体有6个自由度。 3个平动 + 3个转动
1 2
(t
r
v) kT
i 2
kT
刚性分子 v 0 非刚性分子 v 2vk
对于处在温度为T 的平衡态的经典系统,粒子每个
自由度对应的平均能量相等,均为 k T / 2
五、能量均分定理
自由度 分子
单原子分子
刚性双原子分子
非刚性双原子 分子
刚性三原子分子
非刚性三原子 分子
t 平动
3 3 3 3 3
