大学物理 麦克斯韦分子速率分布定律
合集下载
大学物理第十二章气体动理论第6节 麦克斯韦气体分子速率分布律
解
m(H 2 ) m(O2 ) v p ( H 2 ) v p (O 2 )
vp (H2 ) 2 000m.s-1
2kT vp m
o
2 000
v/ ms
1
vp ( H 2 )
m( O 2 ) 32 4 v p (O 2 ) m( H 2 ) 2
vp (O2 ) 500m.s
f ( v)
dS
dN f ( v)dv dS N
v
第十二章 气体动理论
o
v v dv
概率密度
3
物理学
第五版
12-6 麦克斯韦气体分子速率分布律
f (v)dv物理意义
表示在温度为 T 的平衡状态下,速 率在 v 附近单位速率区间 的分子数占总 数的百分比 .
f (v)dv 的物理意义:
表示速率在 v v dv 区间的分 子数占总分子数的百分比.
第十二章 气体动理论
4
物理学
第五版
12-6 麦克斯韦气体分子速率分布律 麦克斯韦气体分子速率分布律 12-6
dN Nf ( v)dv 速率在 v v dv 内分子数: 速率位于 v1 v2区间的分子数: v2 N v N f (v)dv 1 速率位于 v1 v2 区间的分 f ( v)
-1
第十二章 气体动理论
17
f (v )
vp v v
2
第十二章 气体动理论
vp v 2 v
v
15
物理学
第五版
12-6 麦克斯韦气体分子速率分布律 麦克斯韦气体分子速率分布律 12-6
讨论 1 已知分子数 N ,分子质量 m ,分布函 数 f ( v) . 求 (1) 速率在 vp ~ v 间的分子 数;(2)速率在 vp ~ 间所有分子动能 之和 . 解 ( 1)
6.5 麦氏速率分布率

14 首 页 上 页 下 页退 出
2、质量与分子速率
温度下相同时,分子的质量越大, 温度下相同时,分子的质量越大,分布 曲线中的最概然速率v 就越小。 曲线中的最概然速率 p 就越小。 但归一化条件要求曲线下总面积不变, 但归一化条件要求曲线下总面积不变, 因此分布曲线宽度减小,高度升高。 因此分布曲线宽度减小,高度升高。
0 −100 (m/ s), 100 − 200(m/ s) , 200 − 300(m/ s)L L
1 首 页 上 页 下 页退 出
2)求气体在平衡态下分布在各速率区间内的分子数 2)求气体在平衡态下分布在各速率区间内的分子数 ∆N 3)各区间内的分子数占气体分子总数的百分比 3)各区间内的分子数占气体分子总数的百分比 4)各区间内每单位速率区间的分子数占 4)各区间内每单位速率区间的分子数占 气体分子总数的百分比。 气体分子总数的百分比。 描述速率分布的方法如下: 描述速率分布的方法如下: 1)根据实验数据列表——分布表(例见课本P209表6.1) 根据实验数据列表——分布表(例见课本P209表6.1) ——分布表 P209 2)根据分布表作出曲线——分布曲线 根据分布表作出曲线 分布曲线 3)由分布曲线找出函数关系——分布函数 由分布曲线找出函数关系——分布函数 ——
v2 ∆N = ∫ f (v) dv v1 N
6 首 页 上 页 下 页退 出
dN dN ⋅ dv = Ndv N
f (v)
f (v)的最大值
分子速率出现 在v-v+dv 区 间内的概率
f (vp )
v1 v2 v p
v2 ∆N = ∫ f (v)dv v1 N
v v+ dv
分子出现在v 分子出现在 1-v2 区 间内的概率
7-6麦克斯韦气体分子速率分布定律剖析.

7 – 6 麦克斯韦气体分子速率分布率
物理学教程 (第二版)
f (v)
S
o
v1 v2
dN f (v)dv dS N 速率位于v v dv 内分子数
v
dN Nf (v)dv
速率位于
v1
v2
区间的分子数
N
v2
v1
N
f
(v)dv
速率位于 v1 v2 区间的分子数占总数的百分比
第七章 气体动理论
f (v) dN Ndv
f (v)
o
v
7 – 6 麦克斯韦气体分子速率分布率
物理学教程 (第二版)
二 三种统计速率
1)最概然速率 v p
df (v) 0 dv vvp
根据分布函数求得
f (v)
f max
o
vp
v
M mNA , R NA k
vp
2kT 1.41 kT
v
N2 分子在不同温 度下的速率分布
第七章 气体动理论
f (v)
O2 H2
o vp0 vpH
v
同一温度下不同 气体的速率分布
7 – 6 麦克斯韦气体分子速率分布率
物理学教程 (第二版)
例 计算在 27 C 时,氢气和氧气分子的方均
根速率 vrms .
解 MH 0.002kg mol1
MO 0.032kg mol1
8kT
0
πm
o
v
v 1.60 kT 1.60 RT
m
M
第七章 气体动理论
7 – 6 麦克斯韦气体分子速率分布率
物理学教程 (第二版)
大学物理麦克斯韦分子速率分布定律资料

(D) 速率大小与最概然速率相近的气体分子的比 率最大.
11
例: 设有N个气体分子,其速率分布函数为
f
(
)
A
(0 0
)
0 0 0
求: (1)常数A;(2)最概然速率,平均速率和方均根;
(3)速率介于0~0/3之间的分子数;(4)速率介于0~ 0/3
之间的气体分子的平均速率。
f()
解: (1)气体分子的分布曲线如图
2 1300
N
dN
0
3 Nf ( )d
0
0 3
0
N
6
3 0
(0
)d
7N 27
13
(4)速率介于0~0/3之间的气体分子平均速率为
0~0 3
0
3 dN
0 0
0 3
0
N
6 v03
2
(
0
)d
30
7N 27
14
3 dN 0
注意:速率介于 1~ 2之间的气体分子的平均速率
的计算是
2f ( )d
1~2
1
2 f ( )d
1
而非
1 ~2
2f ( )d
1
14
作业题
设. 有N个粒子,其速率分布函数 f v 为
f
v
Av 30 v
0
v 30 v 30
求: (1)归一化常数A的值;(2)最概然速率
(3)N个粒子的平均速率 v
15
§3.4 麦克斯韦分子速率分布定律
任何一个分子,速度大小和方向都是偶然的, 不可预知。但在平衡态下,大量气体分子的速度分布 将具有稳定的规律 — 麦克斯韦速度分布律。
只考虑速度大小的分布—麦克斯韦速率分布律。
11
例: 设有N个气体分子,其速率分布函数为
f
(
)
A
(0 0
)
0 0 0
求: (1)常数A;(2)最概然速率,平均速率和方均根;
(3)速率介于0~0/3之间的分子数;(4)速率介于0~ 0/3
之间的气体分子的平均速率。
f()
解: (1)气体分子的分布曲线如图
2 1300
N
dN
0
3 Nf ( )d
0
0 3
0
N
6
3 0
(0
)d
7N 27
13
(4)速率介于0~0/3之间的气体分子平均速率为
0~0 3
0
3 dN
0 0
0 3
0
N
6 v03
2
(
0
)d
30
7N 27
14
3 dN 0
注意:速率介于 1~ 2之间的气体分子的平均速率
的计算是
2f ( )d
1~2
1
2 f ( )d
1
而非
1 ~2
2f ( )d
1
14
作业题
设. 有N个粒子,其速率分布函数 f v 为
f
v
Av 30 v
0
v 30 v 30
求: (1)归一化常数A的值;(2)最概然速率
(3)N个粒子的平均速率 v
15
§3.4 麦克斯韦分子速率分布定律
任何一个分子,速度大小和方向都是偶然的, 不可预知。但在平衡态下,大量气体分子的速度分布 将具有稳定的规律 — 麦克斯韦速度分布律。
只考虑速度大小的分布—麦克斯韦速率分布律。
麦克斯韦气体速率分布律推导

麦克斯韦气体速率分布律推导麦克斯韦-玻尔兹曼速率分布律描述了理想气体中分子速度的统计分布。
以下是该分布律的推导过程。
首先,考虑一个由大量相同分子组成的理想气体,这些分子在容器中随机、无序地运动。
由于分子间的碰撞非常频繁,我们可以假定每个分子的运动是相互独立的。
我们的目标是求出分子速率的分布函数。
1. 假设分子的运动是三维的随机运动,并且分子间无相互作用力。
2. 假设分子的运动是各向同性的,即在任何方向上运动的概率都是相等的。
3. 假设分子的运动是稳定的,即分子的速率分布不随时间改变。
4. 引入分子速度的微分元素d³v,表示速度在v到v+dv之间的分子数。
5. 引入微元体积元素dV和微元时间元素dt。
接下来,我们将使用微元分析法来推导速率分布律。
对于一个具有速率v的分子,在时间dt内,它将沿着速度方向移动的距离为v·dt。
因此,它所扫过的体积元素为dV = v²·cos²(θ)·sin(θ)·dv·dt,其中θ是速度方向与某一选定方向(通常是x轴)的夹角。
现在,考虑在dt时间内所有具有速率v的分子所扫过的体积总和,即所有可能的方向θ的贡献。
由于θ的取值范围是0到π,我们可以将上述体积元素乘以角度元素dθ(从0到π)并积分,以得到总的体积元素dV_total:dV_total = ∫(v²·cos²(θ)·sin(θ)·dv)·dθ·dt由于cos²(θ)·sin(θ)是关于θ的偶函数,而在0到π的范围内积分,它的积分结果为零。
为了解决这个问题,我们需要考虑在速度方向上的微小位移。
在速度方向上的微小位移为v·cos(θ)·dt,因此,在dt时间内,具有速率v的分子在速度方向上的微小体积元素为dV_v = v·cos(θ)·dv·dt。
大学物理,气体动理论14-06 麦克斯韦气体分子速率分布律

i ~ i 1
N i
N i N
5
14.6 麦克斯韦速率分布律
第14章 气体动理论
气体分子按速率分布的统计规律最早是由麦克 斯韦于1859年在概率论的基础上导出的,1877年玻 耳兹曼由经典统计力学导出。 由于技术条件的限制,测定气体分子速率分布 的实验,直到20世纪二十年代才实现。 1920年斯特 恩首先测出银蒸汽分子的速率分布;1934年我国物 理学家葛正权测出铋蒸汽分子的速率分布;1955年 密勒和库士测出钍蒸汽分子的速率分布。 斯特恩实验是历史上最早验证麦克斯韦速率分 布律的实验。实验证实了麦克斯韦的分子按速率分 布的统计规律。
14.6 麦克斯韦速率分布律
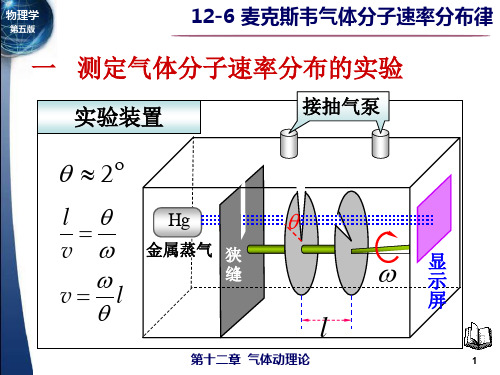
一 测定气体分子速率分布的实验
第14章 气体动理论
实验装置
接抽气泵
2
l v
Hg
金属蒸汽 狭 缝
v l
显 示 屏
8
l
14.6 麦克斯韦速率分布律
第14章 气体动理论
9
14.6 麦克斯韦速率分布律
测量原理
第14章 气体动理论
(1) 能通过细槽到达检测 器的分子所满足的条件 L v L v (2) 通过改变角速度ω的 大小,选择速率 v
28
14.6 麦克斯韦速率分布律
第14章 气体动理论
求:速率在 v1 ~ v2 之间的分子的平均速率。
(3) 通过细槽的宽度,选择不同的速率区间 L v v 2
(4) 沉积在检测器上相应的金属层厚度必定正比 相应速率下的分子数。
10
14.6 麦克斯韦速率分布律
速率区间 (m/s) 实验数据 氧分子在 273K时的 速率分布
11.4-11.6 麦克斯韦速率分布规律 麦克斯韦-波尔兹曼分布律、分子平均碰撞次数和平均自由程

1)
v
vp
Nf
(v)dv
2)
vp
1 2
mv 2
Nf
(v)dv
例 如图示两条 f (v) ~ v 曲线分别表示氢气和
氧气在同一温度下的麦克斯韦速率分布曲线, 从图
上数据求出氢气和氧气的最可几速率 .
f (v) O2
H2
vp
2RT M mol
M mol (H2 ) M mol (O2 )
469.1m / s
由公式
v2 3RT M mol
v2
38.31 300 29 103
507.1m
/
s
例 已知分子数 N ,分子质量 m ,分布函数
f (v) 求 1) 速率在vp ~ v 间的分子数; 2)速率
在 vp ~ 间所有分子动能之和 .
解:速率在v v dv 间的分子数 dN Nf (v)dv
N
dN
0
dN
f ()d
N
0N 0
8kT 8RT 1.60 RT
m
M mol
M mol
3
2dN
0
2
f
(
)d
N
0
或由w 1 m2 3 kT
2
2
可得 2 3kT
v1~v2
v2 f ()d
v1
v2 f ()d
v1
v v1~v2
v2 vf (v)dv
v1
对于v的某个函数g(v),一般地,其平均值可以表示为
7-(4-5)麦克斯韦速率分布

(1) 不同温度下的同种气体
f (v)
T 1
T2 > T 1
T2
v
T > T2 , orT < T2 ? 1 1
vp1 = 2RT 1
vp1 vp2
2RT2
µ
vp2 =
µ
vp1 < vp2
T < T2 1
第六章 气体动理学理论 (2) 同温度下的不同种气体
f (v)
O2 , H2 ?
1
2RT
2
v
vp1 vp2
对于一定量的气体,在温度为T的平衡态下 的平衡态下, 对于一定量的气体,在温度为 的平衡态下,气体分子速率 出现在v附近 单位速率区间内的分子数dN 附近、 出现在 附近、单位速率区间内的分子数
说出下列各式的物理意义
第六章 气体动理学理论
(4)∫ f (v)dv= ∫
v1
v2
v2
v1
∆Nv1 →v2 dN dv = Ndv N
对于一定量的气体,在温度为 的平衡态下 的平衡态下, 对于一定量的气体,在温度为T的平衡态下,气体分子速率 占总分子数N的百分比 概率 概率)。 v1~v2区间内的分子数△N占总分子数 的百分比 (概率 。 占总分子数
(5)∫ Nf (v)dv = ∫
v1
v2
dN N = ∆Nv1→v2 N
对于一定量的气体,在温度为T的平衡态下 的平衡态下, 对于一定量的气体,在温度为 的平衡态下,气体分子速率 v1~v2区间内的分子数△N。 。
一、分子速率分布函数
速率分布: 速率分布:各种不同速率范围内的分子数占总分子数的 百分比为多大。 百分比为多大。
伽 耳 顿 板
第六章 气体动理学理论
f (v)
T 1
T2 > T 1
T2
v
T > T2 , orT < T2 ? 1 1
vp1 = 2RT 1
vp1 vp2
2RT2
µ
vp2 =
µ
vp1 < vp2
T < T2 1
第六章 气体动理学理论 (2) 同温度下的不同种气体
f (v)
O2 , H2 ?
1
2RT
2
v
vp1 vp2
对于一定量的气体,在温度为T的平衡态下 的平衡态下, 对于一定量的气体,在温度为 的平衡态下,气体分子速率 出现在v附近 单位速率区间内的分子数dN 附近、 出现在 附近、单位速率区间内的分子数
说出下列各式的物理意义
第六章 气体动理学理论
(4)∫ f (v)dv= ∫
v1
v2
v2
v1
∆Nv1 →v2 dN dv = Ndv N
对于一定量的气体,在温度为 的平衡态下 的平衡态下, 对于一定量的气体,在温度为T的平衡态下,气体分子速率 占总分子数N的百分比 概率 概率)。 v1~v2区间内的分子数△N占总分子数 的百分比 (概率 。 占总分子数
(5)∫ Nf (v)dv = ∫
v1
v2
dN N = ∆Nv1→v2 N
对于一定量的气体,在温度为T的平衡态下 的平衡态下, 对于一定量的气体,在温度为 的平衡态下,气体分子速率 v1~v2区间内的分子数△N。 。
一、分子速率分布函数
速率分布: 速率分布:各种不同速率范围内的分子数占总分子数的 百分比为多大。 百分比为多大。
伽 耳 顿 板
第六章 气体动理学理论
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
p
2kT m
0
2 RT RT 1.41 M mol M mol
6
2.平均速率 分立:平均速率 i Ni
N
连续: i , △ Ni dN=Nf ()d , ∑→∫
N
0
dN
N
N
0
dN f ( ) d 0 N
1/ 2
e 1
当气体温度T一定时,不同分子 p M mol Mmol1 <Mmol2 <Mmol3 f ( p )
Mmol3
f(v) Mmol2 T相同, Mmol1<Mmol2<Mmol3 Mmol1
v
10
讨论 麦克斯韦速率分布中最概然速率
vp
的概念
下面哪种表述正确?
(A) p 是气体分子中大部分分子所具有的速率. (B) 是速率最大的速度值. p (C) p 是麦克斯韦速率分布函数的最大值.
v v v
(D) 速率大小与最概然速率相近的气体分子的比
率最大.
11
例:
设有N个气体分子,其速率分布函数为 A ( 0 ) 0 0 f ( ) 0 0 求: (1)常数A;(2)最概然速率,平均速率和方均根; (3)速率介于0~0/3之间的分子数;(4)速率介于0~ 0/3 之间的气体分子的平均速率。
4
2
3kT m
3 RT RT 1.73 M mol M mol
讨论分布函数的特征用p 讨论分子的平均平动动能用 讨论分子碰撞问题时用
8
2
四、麦克斯韦速率分布曲线的性质
p
2 RT M mol
8m f ( p ) π kT
1/ 2
8 M mol e 1 π RT
v 30 v 30
求: (1)归一化常数A的值;(2)最概然速率 (3)N个粒子的平均速率 v
15
1.4 8.1 16.5 21.4 20.6 15.1 9.2
7~8
4.8
8~9
2.0
9以上
0.9
%
•把速率分成若干相等区间 ~+ △ •在平衡态下,气体分布在各区间内的分子数△N
1
•各区间的分子数△N占气体分子总数N的百分比
N N
其值与及△有关
ΔN NΔ
消除△的影响后
N N
§3.4 麦克斯韦分子速率分布定律
任何一个分子,速度大小和方向都是偶然的, 不可预知。但在平衡态下,大量气体分子的速度分布 将具有稳定的规律 — 麦克斯韦速度分布律。 只考虑速度大小的分布—麦克斯韦速率分布律。
一. 速率分布函数
0 ℃ 时,氧气分子速率分布的粗略情况
100 m/s
1以下 1~2 2~3 3~4 4~5 5~6 6~7
f()
解: (1)气体分子的分布曲线如图 由归一化条件
0
0Leabharlann 0f ( )d 1
0
0
A 3 A ( 0 )d 0 1 6
6 A 3 0
12
(2)最概然速率 df ( ) A( 0 2 ) v 0 p d v p 平均速率
p
0
t D
D
D l 2
5
D 2 l 2
三.分子速率的三个统计值
1.最概然速率p 速率分布函数 f() 极大值对应的速率p称为最 概然速率 f()
d f ( ) d
T,m 一定
P
0
p
在单位速率区间内,处在 最概然速率 p 附近的分子数 占总分子数的百分比最大。
2
麦克斯韦速率分布律
dN m 3/2 f ( )d 4 ( ) e N 2 kT
m 2 2 kT
f()
2 d
T,m 一定
麦氏速率分布曲线
+d
4
测定分子速率分布的实验装置
真空室
B
S
G P
P
A
分子源
圆筒
G是弯曲玻璃板,沉积射到它上面的各种速率的分子。 圆筒不转动时,分子束中的分子都射在G板的P处。 圆筒转动,分子束的速率不同的分子将射在不同位置.
注意:速率介于 1~ 2之间的气体分子的平均速率 的计算是 2
~
1
2
f ( )d f ( )d
1 2 1
而非
~ f ( )d
1 2
2
1
14
作业题
设有N个粒子,其速率分布函数 f v 为
.
Av 30 v f v 0
1/ 2
e 1
p 当分子的Mmol 一定时 T f ( p ) 73K 273K f() Mmol相同
1273K
9
p
2 RT M mol
8m f ( p ) π kT
1/ 2
e
1
8 M mol π RT
f ( )d
0
将麦氏速率分布函数式代入得
8kT 8 RT RT 1.60 m M mol M mol
7
3.方均根速率
2 f ( )d
2 0
m 3/ 2 4 ( ) e 0 2kT
2
mv 2 2 kT
3kT d m
N dN Nf ( )d 7N N 3 ( 0 )d 0 27
13
6
(4)速率介于0~0/3之间的气体分子平均速率为
0~
0
3
0 3 0 0 3 0
dN
dN
0 3 0
6 2 N 3 ( 0 )d 3 0 v0 7 N 27 14
2. f ( ) 的性质
0
dN N
dN Nf ( )d
0
Nf ( )d N
0
f ( )d 1
分布函数的归一化条件
3
二.麦克斯韦速率分布规律
1859年麦克斯韦导出了理想气体在无外场的平 衡态(T)下,分子速率分布函数为: m — 气体 m 3/2 mkT 2 f ( ) 4 ( ) e 2 分子的质量 2 kT
2
f ( )d
0
0
0
6 2 ( 0 )d 3 0
0
0 2
3 0 10
2
方均速率
f ( )d
2 2 0
0 3 0
0
6 3 ( 0 )d 3 0
0 3 0
(3)速率介于0~0/3之间的分子数
只与有关
0
dN f ( ) Nd
N 1 dN f ( ) lim 0 N N d
~ +△
dN f ( ) Nd
分子的速率分布函数
f()d
0
~ +d
2
1.速率分布函数的物理意义 表示分布在速率附近单位速率区间内的分子数 占总分子数的百分比 对于一个分子来说,f () 就是分子处于速率附 近单位速率区间的概率,也称为概率密度。
2kT m
0
2 RT RT 1.41 M mol M mol
6
2.平均速率 分立:平均速率 i Ni
N
连续: i , △ Ni dN=Nf ()d , ∑→∫
N
0
dN
N
N
0
dN f ( ) d 0 N
1/ 2
e 1
当气体温度T一定时,不同分子 p M mol Mmol1 <Mmol2 <Mmol3 f ( p )
Mmol3
f(v) Mmol2 T相同, Mmol1<Mmol2<Mmol3 Mmol1
v
10
讨论 麦克斯韦速率分布中最概然速率
vp
的概念
下面哪种表述正确?
(A) p 是气体分子中大部分分子所具有的速率. (B) 是速率最大的速度值. p (C) p 是麦克斯韦速率分布函数的最大值.
v v v
(D) 速率大小与最概然速率相近的气体分子的比
率最大.
11
例:
设有N个气体分子,其速率分布函数为 A ( 0 ) 0 0 f ( ) 0 0 求: (1)常数A;(2)最概然速率,平均速率和方均根; (3)速率介于0~0/3之间的分子数;(4)速率介于0~ 0/3 之间的气体分子的平均速率。
4
2
3kT m
3 RT RT 1.73 M mol M mol
讨论分布函数的特征用p 讨论分子的平均平动动能用 讨论分子碰撞问题时用
8
2
四、麦克斯韦速率分布曲线的性质
p
2 RT M mol
8m f ( p ) π kT
1/ 2
8 M mol e 1 π RT
v 30 v 30
求: (1)归一化常数A的值;(2)最概然速率 (3)N个粒子的平均速率 v
15
1.4 8.1 16.5 21.4 20.6 15.1 9.2
7~8
4.8
8~9
2.0
9以上
0.9
%
•把速率分成若干相等区间 ~+ △ •在平衡态下,气体分布在各区间内的分子数△N
1
•各区间的分子数△N占气体分子总数N的百分比
N N
其值与及△有关
ΔN NΔ
消除△的影响后
N N
§3.4 麦克斯韦分子速率分布定律
任何一个分子,速度大小和方向都是偶然的, 不可预知。但在平衡态下,大量气体分子的速度分布 将具有稳定的规律 — 麦克斯韦速度分布律。 只考虑速度大小的分布—麦克斯韦速率分布律。
一. 速率分布函数
0 ℃ 时,氧气分子速率分布的粗略情况
100 m/s
1以下 1~2 2~3 3~4 4~5 5~6 6~7
f()
解: (1)气体分子的分布曲线如图 由归一化条件
0
0Leabharlann 0f ( )d 1
0
0
A 3 A ( 0 )d 0 1 6
6 A 3 0
12
(2)最概然速率 df ( ) A( 0 2 ) v 0 p d v p 平均速率
p
0
t D
D
D l 2
5
D 2 l 2
三.分子速率的三个统计值
1.最概然速率p 速率分布函数 f() 极大值对应的速率p称为最 概然速率 f()
d f ( ) d
T,m 一定
P
0
p
在单位速率区间内,处在 最概然速率 p 附近的分子数 占总分子数的百分比最大。
2
麦克斯韦速率分布律
dN m 3/2 f ( )d 4 ( ) e N 2 kT
m 2 2 kT
f()
2 d
T,m 一定
麦氏速率分布曲线
+d
4
测定分子速率分布的实验装置
真空室
B
S
G P
P
A
分子源
圆筒
G是弯曲玻璃板,沉积射到它上面的各种速率的分子。 圆筒不转动时,分子束中的分子都射在G板的P处。 圆筒转动,分子束的速率不同的分子将射在不同位置.
注意:速率介于 1~ 2之间的气体分子的平均速率 的计算是 2
~
1
2
f ( )d f ( )d
1 2 1
而非
~ f ( )d
1 2
2
1
14
作业题
设有N个粒子,其速率分布函数 f v 为
.
Av 30 v f v 0
1/ 2
e 1
p 当分子的Mmol 一定时 T f ( p ) 73K 273K f() Mmol相同
1273K
9
p
2 RT M mol
8m f ( p ) π kT
1/ 2
e
1
8 M mol π RT
f ( )d
0
将麦氏速率分布函数式代入得
8kT 8 RT RT 1.60 m M mol M mol
7
3.方均根速率
2 f ( )d
2 0
m 3/ 2 4 ( ) e 0 2kT
2
mv 2 2 kT
3kT d m
N dN Nf ( )d 7N N 3 ( 0 )d 0 27
13
6
(4)速率介于0~0/3之间的气体分子平均速率为
0~
0
3
0 3 0 0 3 0
dN
dN
0 3 0
6 2 N 3 ( 0 )d 3 0 v0 7 N 27 14
2. f ( ) 的性质
0
dN N
dN Nf ( )d
0
Nf ( )d N
0
f ( )d 1
分布函数的归一化条件
3
二.麦克斯韦速率分布规律
1859年麦克斯韦导出了理想气体在无外场的平 衡态(T)下,分子速率分布函数为: m — 气体 m 3/2 mkT 2 f ( ) 4 ( ) e 2 分子的质量 2 kT
2
f ( )d
0
0
0
6 2 ( 0 )d 3 0
0
0 2
3 0 10
2
方均速率
f ( )d
2 2 0
0 3 0
0
6 3 ( 0 )d 3 0
0 3 0
(3)速率介于0~0/3之间的分子数
只与有关
0
dN f ( ) Nd
N 1 dN f ( ) lim 0 N N d
~ +△
dN f ( ) Nd
分子的速率分布函数
f()d
0
~ +d
2
1.速率分布函数的物理意义 表示分布在速率附近单位速率区间内的分子数 占总分子数的百分比 对于一个分子来说,f () 就是分子处于速率附 近单位速率区间的概率,也称为概率密度。
