spss实验报告---方差分析
SPSS的方差分析实验报告

实验报告
2 选择菜单:【Analyze】→【Compare Means】→【One-Way ANOVA】,将“月销售额”作为观测变量选入【Dependent List】,将“促销方式”作为控制变量选入【Factor】,选择按钮“Option”,打开对话框,选择方差齐性检验,观测变量的基本统计量,选择输出个水平下观测变量均值的折线图
3 选择“Post Hoc”按钮,选择方差相同和方差不同情况下的多重比较的检验方法,如图所示第三题:
1 根据题目建立某商品在不同地区和不同日期的销售数据的文件,如图
2 选择菜单:【Analyze】→【General Linear Model】→【Univariate】,将“销售量”选入【Dependent Variable】,将“地区和日期”选入【Fixed Factor(s)】,选择“Options”,在【Display】中选择“Homogeneity tests”。
如图所示
四、实验结果及分析(最好有截图):
第一题:
(1) 0.000<0.005拒绝原假设.说明不同的促销方式是对该类商品销售量的增长有显著影响
(2) 特价销售的促销方式好
(3)
第三题:
(1) 建立数据文件如图
(2)地区0.313>0.05,接受原假设。
地区对销售量没有显著性影响
日期0.254>0.05,接受原假设。
日期对销售量没有显著性影响
地区和日期0.000<0.05,拒绝原假设。
地区和日期的交互作用对销售量有显著性影响。
spss 方差分析(多因素方差分析)实验报告

大学经济管理学院学生实验报告实验课程名称:统计软件及应用专业工商管理班级学号姓名成绩实验地点实验性质:演示性 验证性综合性设计性实验项目名称方差分析(多因素方差分析)指导教师一、实验目的掌握利用SPSS 进行单因素方差分析、多因素方差分析的基本方法,并能够解释软件运行结果。
二、实验内容及步骤(包括实验案例及基本操作步骤)实验案例:为研究某商品在不同地区和不同日期的销售差异性,调查收集了以下日平均销售量数据。
销售量日期周一至周三周四至周五周末地区一5000 6000 4000 6000 8000 3000 4000 7000 5000地区二700080008000500050006000500060004000地区三300020004000600060005000800090006000(1)选择恰当的数据组织方式建立关于上述数据的SPSS数据文件。
在SPSS输入数据。
(2)利用多因素方差分析法,分析不同地区和不同日期对该商品的销售是否产生了显著影响。
1. 选择菜单Analyze,General Linear Model,Univariate;2. 指定观测变量销售额到Dependant Variable框中;3. 指定固定效应的控制变量到Fixed Factors框中,4. OK,得到分析结果。
(3)地区和日期是否对该商品的销售产生了交互影响?若没有显著的交互影响,则试建立非饱和模型进行分析,并与饱和模型进行对比。
三、实验结论(包括SPSS输出结果及分析解释)SPSS输出的多因素方差分析的饱和模型分析:表的第一列是对观测变量总变差分解的说明;第二列是观测变量变差分解的结果;第三列是自由度;第四列是方差;第五列是F检验统计量的观测值;第六列是检验统计量的概率P-值。
F日期,,F地区,F日期*地区概率P-值分别为0.254,0.313,0.000。
如果显著性水平α为0.05,由于F日期、,F地区大于显著性水平α,所以不应拒绝原假设,不同地区和不同日期对该商品没有显著性影响。
实习 二(方差分析)
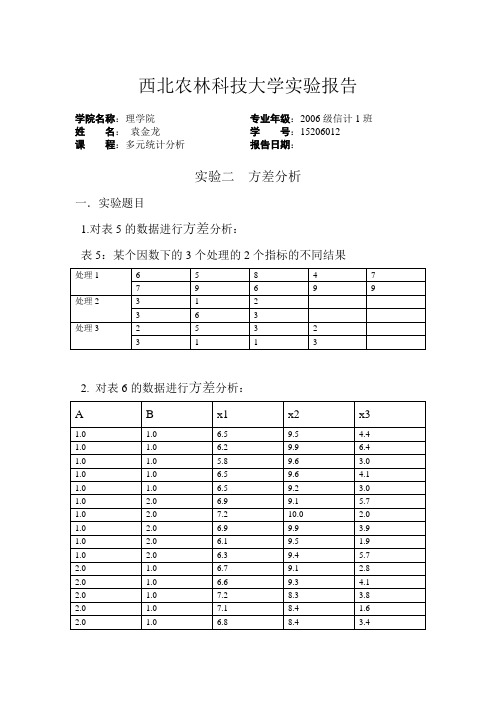
西北农林科技大学实验报告学院名称:理学院专业年级:2006级信计1班姓名:袁金龙学号:15206012课程:多元统计分析报告日期:实验二方差分析一.实验题目1.对表5的数据进行方差分析:表5:某个因数下的3个处理的2个指标的不同结果2. 对表6的数据进行方差分析:二、实验分析:1.从题目要求来看,该题属于单向分类多元方差分析,根据spss软件,得到如下结果:⑴数据输入:⑵spss操作步骤:选择[Analyze]=>[General Linear Model]=>[Multivariate...],打开[Multivariate...]主对话框(如图1所示)。
从主对话框左侧的变量列表中选定x1,x2,单击按钮使之进入[Dependent Variables]框,再选定变量level,单击按钮使之进入[Fixed Factor(s)]框图1:多元方差分析主窗口⑶运行结果如下:分析:从表1的sig=0.942>0.05,以及表3的四个统计量的sig最大值为0.003小于0.05,因此,该因数下的3个处理水平的均值不全相同,即该因素下的不同水平间有显著差异,则下面的各指标的比较以及指标内部的比较才有意义。
从表2的x1,x2的sig值为:0.658,0.563大于0.05,则表明指标1与指标2的各自3个不同的处理间有显著的差异。
从表4可以看出:原理(sig<0.05表明该指标下的两个处理间显著,sig>0.05表明该指标下的两个处理间不太显著,sig越小越显著),则指标1下:处理1与处理2之间显著,处理1与处理3之间不显著,处理2与处理3之间不显著;指标2下:处理1与处理2之间显著, 处理1与处理3之间显著, 处理2与处理3之间不显著。
2.从题目要求来看,该题属于两向分类多元方差分析,根据spss软件,得到如下结果:⑴spss操作步骤:选择[Analyze]=>[General Linear Model]=>[Multivariate...],打开[Multivariate...]主对话框(如图1所示)。
用SPSS作方差分析

方差分析表 自由度 df r-1 nT-r nT-1
自由度 df 2 15 17
均方 MS MSTR MSE
F值 MSTTR/MSE
均方
F值
MS
258.00
9.00
28.67
总平方和 = 处理平方和 + 误差平方和
SST = SSA + SSE
r nj
j1 i1
组内估计不受原假设影响,H0为真或为假, 组内估计总是σ2的无偏估计。
___
x 1 1
___
2 x 2
___
x 3 3
___
x 4 4
2的组间估计量 F 2的组内估计量 服从分子自由度为 r 1 ,分母自由度为 nT r 的 F 分布。
(25.25)自由度
(5.5)自由度 (2.1)自由度
20个地块的小麦产量(公斤)
化肥 地块
1 2 3 4 5
鸿福
27.9 25.1 28.5 24.2 26.5
祥丰
26.5 28.7 25.1 29.1 27.2
云天
31.2 28.3 30.8 27.9 29.6
可富
30.8 29.6 32.4 31.7 32.8
样本均值 样本方差 总样本均值
x1 =26.44 s12 =3.298
nT r
nT r
18 3 15
F MSA MSE
F 统计量服从 F 分布,其分子自由度为r 1,分母自由度为 nT r。
F MSA 258 9.00 MSE 28.67
MSA
0
F
MSE
方差 来源 组间 组内 总差异
方差 来源 组间 组内 总差异
SPSS实验3-单因素方差分析

SPSS作业3:方差分析不同学校专业类别对报名人数的分析(一)单因素方差分析基本操作:(1)选择菜单Analyz e-Compare means―One-Way ANOVA;(2)分别选择“报名人数”“专业类别”和“报名人数”“学校”做分析,结果如下:a.专业类别对报名人数的单因素方差分析结果b.不同学校对报名人数的单因素方差分析结果1分析:提出零假设―选择检验统计量―计算检验统计量的观测值及概率p值―给出显著性水平a,做出决策。
零假设:不同专业类别对报名人数没有显著影响;备择假设:不同专业类别对报名人数有显著影响。
图a是专业类别对报名人数的单因素方差分析结果。
可以看出,报名人数的总离差平方和为2.617E8;如果仅考虑专业类别单个因素的影响,则报名人数总变差中,专业类别可解释的变差为5.866E7,抽样误差引起的变差为2.030E8,他们的方差分别为1.955E7和1450230.159,相除所得的F统计量为13.483,对应的p值近似为0。
如果显著水平为a=0.05,由于p值小于a,则应拒绝原假设,认为不同专业类别对报名人数产生了显著影响,它对报名人数的影响效应应不全为0。
零假设:不同学校对报名人数没有显著影响:备择假设:不同学校对报名人数有显著影响。
图b是不同学校对报名人数的单因素方差分析结果。
可以看出,报名人数的总离差平方和为2.617E8;如果仅考虑学校单个因素的影响,则报名人数总变差中,不同学校可解释的变差为9.265E7,抽样误差引起的变差为1.690E8,他们的方差分别为5450179.739和1341587.302,相除所得的F统计量为4.062,对应的p值近似为0。
如果显著水平为a=0.05,由于p值小于a,则应拒绝原假设,认为不同学校对报名人数产生了显著影响,它对报名人数的影响效应应不全为0。
(二)单因素方差的进一步分析基本操作:在Optio n、Post Hoc、Contrasts框中,选择所需要的计算值,结果如下:不同专业类别对报名人数的基本描述统计量及95%置信区间2分析:在4中不同专业类别中,各有36个样本,其中,经管类的报名人数最多,其次是理工类,然后是艺术类,最少的是文学类。
spss方差分析报告操作示范-步骤-例子

第五节方差分析的SPSS操作一、完全随机设计的单因素方差分析1.数据采用本章第二节所用的例1中的数据,在数据中定义一个group变量来表示五个不同的组,变量math表示学生的数学成绩。
数据输入格式如图6-3(为了节省空间,只显示部分数据的输入):图 6-3 单因素方差分析数据输入将上述数据文件保存为“6-6-1.sav”。
2.理论分析要比较不同组学生成绩平均值之间是否存在显著性差异,从上面数据来看,总共分了5个组,也就是说要解决比较多个组(两组以上)的平均数是否有显著的问题。
从要分析的数据来看,不同组学生成绩之间可看作相互独立,学生的成绩可以假设从总体上服从正态分布,在各组方差满足齐性的条件下,可以用单因素的方差分析来解决这一问题。
单因素方差分析不仅可以检验多组均值之间是否存在差异,同时还可进一步采取多种方法进行多重比较,发现存在差异的究竟是哪些均值。
3.单因素方差分析过程(1)主效应的检验假如我们现在想检验五组被试的数学成绩(math)的均值差异是否显著性,可依下列操作进行。
①单击主菜单Analyze/Compare Means/One-Way Anova…,进入主对话框,请把math选入到因变量表列(Dependent list)中去,把group选入到因素(factor)中去,如图6-4所示:图6-4:One-Way Anova主对话框②对于方差分析,要求数据服从正态分布和不同组数据方差齐性,对于正态性的假设在后面非参数检验一章再具体介绍;One-Way Anova可以对数据进行方差齐性的检验,单击铵钮Options,进入它的主对话框,在Homogeneity-of-variance项上选中即可。
设置如下图6-5所示:图6-5:One-Way Anova的Options对话框点击Continue,返回主对话框。
③在主对话框中点击OK,得到单因素方差分析结果4.结果及解释(1)输出方差齐性检验结果Test of Homogeneity of VariancesMATHLevene Statistic df1 df2 Sig.1.238 4 35 .313上表结果显示,Levene方差齐性检验统计量的值为1.238,Sig=0.313>0.05,所以五个组的方差满足方差齐性的前提条件,如果不满足方差齐性的前提条件,后面方差分析计算F统计量的方法要稍微复杂,本章我们只考虑方差齐性条件满足的情况。
方差分析实验报告

实验报告方差分析学院:参赛队员:参赛队员: 参赛队员: 指导老师:目录一、实验目的 (6)1.了解方差分析的基本容; (6)2.了解单因素方差分析; (6)3.了解多因素方差分析; (6)4.学会运用spss软件求解问题; (6)5.加深理论与实践相结合的能力。
(6)二、实验环境 (6)三、实验方法 (7)1. 单因素方差分析; (7)2. 多因素方差分析。
(7)四、实验过程 (7)问题一: (7)1.1实验过程 (7)1.1.1输入数据,数据处理; (7)1.1.2单因素方差分析 (8)1.2输出结果 (9)1.3结果分析 (10)1.3.1描述 (10)1.3.2方差性检验 (10)1.3.3单因素方差分析 (10)问题二: (10)2.1实验步骤 (11)2.1.1命名变量 (11)2.1.2导入数据 (11)2.1.3单因素方差分析 (12)2.1.4输出结果 (14)2.2结果分析 (15)2.2.1描述 (15)2.2.2方差性检验 (15)2.2.3单因素方差分析 (15)问题三: (15)3.1提出假设 (16)3.2实验步骤 (16)3.2.1数据分组编号 (16)3.2.2多因素方差分析 (17)3.2.3输出结果 (22)3.3结果分析 (23)五、实验总结 (23)方差分析一、实验目的1.了解方差分析的基本容;2.了解单因素方差分析;3.了解多因素方差分析;4.学会运用spss软件求解问题;5.加深理论与实践相结合的能力。
二、实验环境Spss、office三、实验方法1. 单因素方差分析;2. 多因素方差分析。
四、实验过程问题一:用二氧化硒50mg对大鼠染尘后不同时期全肺湿重的变化见下表,试比较染尘后1个月,3个月,6个月,三个时期的全肺湿重有无差别。
1个月3个月6个月3.4 3.4 3.63.64.4 4.44.3 3.45.14.1 4.2 54.2 4.75.53.34.2 4.71.1实验过程1.1.1输入数据,数据处理;1.1.2单因素方差分析选择:分析比较均值单因素AVONA;将变量大鼠全肺湿重放置因变量列表栏中,月份放置因子栏中;两两比较中,勾选最小显著差异法;选项中,勾选描述性,方差同质性检验,welch;1.3.1描述由描述可知,一月份的均值为3.817,标准差为0.4355,三月份的均值为4.050,标准差为0.5357,六月份的均值为4.717,标准差为0.66161.3.2方差性检验由方差齐性检验可知,Sig值=0.826>0.05,说明各组的方差在α=0.05水平上没有显著性差异,即方差具有齐次性1.3.3单因素方差分析根据输出的p值为0.034可以看出,小于0.05,大于0.01,因此拒绝原假设,染尘后1个月,3个月,6个月,三个时期的全肺湿重有无差别有显著性意义,结论是染尘后1个月,3个月,6个月,三个时期的全肺湿重有差别,一个月大鼠的全肺湿重最小,三个月其次,六个月大鼠的全肺湿重最大。
spss方差分析报告操作示范-步骤-例子

第五节方差分析的SPSS操作一、完全随机设计的单因素方差分析1.数据采用本章第二节所用的例1中的数据,在数据中定义一个group变量来表示五个不同的组,变量math表示学生的数学成绩。
数据输入格式如图6-3(为了节省空间,只显示部分数据的输入):图 6-3 单因素方差分析数据输入将上述数据文件保存为“6-6-1.sav”。
2.理论分析要比较不同组学生成绩平均值之间是否存在显著性差异,从上面数据来看,总共分了5个组,也就是说要解决比较多个组(两组以上)的平均数是否有显著的问题。
从要分析的数据来看,不同组学生成绩之间可看作相互独立,学生的成绩可以假设从总体上服从正态分布,在各组方差满足齐性的条件下,可以用单因素的方差分析来解决这一问题。
单因素方差分析不仅可以检验多组均值之间是否存在差异,同时还可进一步采取多种方法进行多重比较,发现存在差异的究竟是哪些均值。
3.单因素方差分析过程(1)主效应的检验假如我们现在想检验五组被试的数学成绩(math)的均值差异是否显著性,可依下列操作进行。
①单击主菜单Analyze/Compare Means/One-Way Anova…,进入主对话框,请把math选入到因变量表列(Dependent list)中去,把group选入到因素(factor)中去,如图6-4所示:图6-4:One-Way Anova主对话框②对于方差分析,要求数据服从正态分布和不同组数据方差齐性,对于正态性的假设在后面非参数检验一章再具体介绍;One-Way Anova可以对数据进行方差齐性的检验,单击铵钮Options,进入它的主对话框,在Homogeneity-of-variance项上选中即可。
设置如下图6-5所示:图6-5:One-Way Anova的Options对话框点击Continue,返回主对话框。
③在主对话框中点击OK,得到单因素方差分析结果4.结果及解释(1)输出方差齐性检验结果Test of Homogeneity of VariancesMATHLevene Statistic df1 df2 Sig.1.238 4 35 .313上表结果显示,Levene方差齐性检验统计量的值为1.238,Sig=0.313>0.05,所以五个组的方差满足方差齐性的前提条件,如果不满足方差齐性的前提条件,后面方差分析计算F统计量的方法要稍微复杂,本章我们只考虑方差齐性条件满足的情况。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验报告
——(方差分析)
一、实验目的
熟练使用SPSS软件进行方差分析。
学会通过方差分析分析不同水平的控制变量是否对结果产生显著影响。
二、实验内容
1、某职业病防治院对31名石棉矿工中的石棉肺患者、可疑患者及非患者进行了用力肺活量(L)测定,问三组石棉矿工的用力肺活量有无差别?(自建数据集)
石棉肺患者可疑患者非患者
1.8
2.3 2.9
1.4
2.1
3.2
1.5
2.1 2.7
2.1 2.1 2.8
1.9
2.6 2.7
1.7
2.5
3.0
1.8
2.3
3.4
1.9
2.4
3.0
1.8
2.4
3.4
1.8 3.3
2.0
3.5
SPSS计算结果:
在建立数据集时定义group1为石棉肺患者,group2为可疑患者,group3为非患者。
零假设:各水平下总体方差没有显著差异。
相伴概率为0.075,大于0.05,可以认为各个组的方差是相等的,可以进行方差检验。
从上表可以看出3个组之间的相伴概率都小于显著性水平0.05,拒绝零假设,说明3个组之间都存在显著差别。
2、某汽车经销商在不同城市进行调查汽车的销售量数据分析工作,每个城市分别处于不同的区域:东部、西部和中部,而且汽车经销商在不同城市投放不同类型的广告,调查数据放置于附件中数据文件“汽车销量调查.sav”。
(1)试分析不同区域与不同广告类型是否对汽车的销量产生显著性的影响?(2)如果考虑到不同城市人均收入具有差异度时,再思考不同区域和不同广告类型对汽车销量产生的影响差异是否改变,这说明什么问题?
SPSS计算结果:
(1)此为多因素方差分析
相伴概率为0.054大于0.05,可以认为各个组总体方差相等可以进行方差检验。
不同地区贡献的离差平方和为7149.781,均方为3574.891;不同广告贡献的离差平方和为7625.708,均方为3812.854。
说明不同广告和不同地区对汽车销量都有显著性影响。
广告对于销量的影响略大于地区对销量的影响。
从地区这个变量比较:
第一组和第三组的相伴概率为0.000,低于显著性水平,一、三组均值差异显著;第二组和第三组的相伴概率为0.028,低于显著性水平,二、三组均值差异显著。
从广告这个变量比较:
第一组和第三组的相伴概率为0.000,低于显著性水平,一、三组均值差异显著;第二组和第三组的相伴概率为0.025,低于显著性水平,二、三组均值差异显著。
从上表中可以看出,地区变量的各个水平之间的相伴概率都小于显著性水平,说明3个地区之间都存在显著差异。
综上所述,不同地区和不同广告对于汽车销量都有显著影响。
(2)此为协方差分析
控制变量为地区和广告类型
协变量为人均收入
控制变量部分:不同地区贡献的离差平方和为350.908,均方为175.454;不同广告贡献的离差平方和为1252.887,均方为626.443;且相伴概率均大于显著性水平0.05,认为没有对销量造成显著差异,均与第一小题中的结果有较大出入。
协变量部分:再看人均收入,贡献的离差平方和为1673.083,均方为1673.083,相伴概率0.016小于显著性水平,表明协变量人均收入对观察结果造成了显著影响。
