第2讲线性回归案例分析
回归分析实例PPT课件

线性回归分析的应用
预测
使用线性回归模型来预测因变 量的值,基于给定的自变量值
。
解释变量关系
通过线性回归分析来了解自变 量与因变量之间的数量关系和 影响程度。
控制变量效应
在实验或调查中,控制自变量 的影响,以观察因变量的变化 情况。
模型的建立和检验
模型的建立
首先需要收集数据,并进行数据 清洗和预处理,然后选择合适的 自变量和因变量,建立逻辑回归
模型。
模型的检验
通过多种检验方法对模型进行评 估,包括参数估计、假设检验、 模型诊断等,以确保模型的准确
性和可靠性。
模型的优化
根据检验结果对模型进行调整和 优化,包括参数调整、变量筛选
详细描述
收集产品在过去一段时间的销售数据,包括销售额、销售量等,作为自变量, 将未来某一段时间的产品销量作为因变量,建立回归模型。通过模型预测未来 产品销量,为企业制定生产和销售计划提供依据。
实例三:疾病风险预测
总结词
基于个人健康数据和疾病历史,建立回归模型预测疾病风险。
详细描述
收集个人的健康数据和疾病历史,包括血压、血糖、胆固醇等生理指标以及家族 病史等信息,作为自变量,将未来患某种疾病的风险作为因变量,建立回归模型 。通过模型预测个人患某种疾病的风险,为预防和早期干预提供参考。
线性关系的假设
自变量x与因变量y之间存在线性关系, 即随着x的增加(或减少),y也相应 地增加(或减少)。
模型的建立和检验
01
02
03
数据收集与整理
收集相关数据,并进行必 要的整理和清洗,以确保 数据的质量和可靠性。
高中数学 第2讲变量的相关性、回归分析及独立性检验

第2讲 变量的相关性、回归分析及独立性检验一、知识回顾1.如何判断两个变量的线性相关:如果在散点图中,2个变量数据点分布在一条直线附近,则这2个变量之间具有线性相关关系。
2.所求直线方程 ˆy=bx +a 叫做回归直线方程;其中 ⋅∑∑∑∑nnii i ii=1i=1nn222iii=1i=1(x-x)(y -y)x -nx yb ==,a =y -bx (x-x)x-nxy回归直线方程必过中心点(,)x y3.相关系数的∑nii (x-x)(y -y)r =性质• (1)|r|≤1.(2)|r|越接近于1,相关程度越大;|r|越接近于0,相关程度越小.4. ˆˆ=-i i y y i 残差e=实际值-预测值2^^211()===-∑∑nniiii i e y y 总残差平方和:残差平方和越小,即模型拟合效果越好5. 两个分类变量的独立性检验:(1)假设结论不成立,即“两个分类变量没有关系”.(2)在此假设下计算随机变量 22n(ad -bc)K =(a +b)(c +d)(a +c)(b +d)(3) 根据随机变量K 2查表得“两个分类变量没有关系”的概率,用1减去此概率即得有联系的概率 典型例题:例1.(宁夏海南卷)对变量x, y 有观测数据理力争(,)(i=1,2,…,10),得散点图1;对变量u ,v 有观测数据(,)(i=1,2,…,10),得散点图2. 由这两个散点图可以判断( )。
(A )变量x 与y 正相关,u 与v 正相关 (B )变量x 与y 正相关,u 与v 负相关 (C )变量x 与y 负相关,u 与v 正相关 (D )变量x 与y 负相关,u 与v 负相关1x 1y 1u 1v变式1. (韶关一模文、理)甲、乙、丙、丁四位同学各自对A 、B 两变量的线性相关性作试验,)()A 甲 ()B 乙 ()C 丙 ()D 丁 例2.一系列样本点(,)(1,2,,)=⋅⋅⋅i i x y i n 的回归直线方程为23,∧=-y x 若117==∑nii X则1==∑ni i y变式1.某地第二季各月平均气温(℃)与某户用水量(吨)如下表,根据表中数据,用最小二乘法求得用水量关于月平均气温的线性回归方程是( )A B. C. D. 例3.下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x (吨)与相应的生产能耗y (吨标准煤)的几组对照数据.(1)请画出上表数据的散点图;(2)请根据上表提供的数据,用最小二乘法求出y 关于x 的线性回归方程ˆˆy bxa =+; (3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤? (参考数值:3 2.543546 4.566.5⨯+⨯+⨯+⨯=)例4.(惠州一模)对196个接受心脏搭桥手术的病人和196个接受血管清障手术的病人进行了3年的跟踪x y y x 5.115ˆ-=x y5.115.6ˆ-=x y 5.112.1ˆ-=x y5.113.1ˆ-=x y0.0005300035000.00030.0004200015000.00020.0001400025001000月收入(元)频率/组距 第2讲 变量的相关性、回归分析及独立性检验课后作业:姓名: 学号:1.若施化肥量x 与小麦产量y 之间的回归直线方程为ˆ2504yx =+,当施化肥量为50kg 时,预计小麦产量为2.下表是某厂1~4月份用水量(单位:百吨)的一组数据:月份x1 2 3 4用水量y5.443 5.2由散点图可知,用水量y 与月份x 之间有较好的线性相关关系,其线性回归直线方程是a x y +-=∧7.0,则=a3.一组数据的平均数是2.8,方差是3.6,若将这组数据中的每一个数据都加上60,得到一组新数据,则所得新数据的平均数和方差分别是( )A .57.2 3.6B .57.2 56.4C .62.8 63.6D .62.8 3.64.有一笔统计资料,共有11个数据如下(不完全以大小排列):2,4,4,5,5,6,7,8,9,11,x ,已知这组数据的平均数为6,则这组数据的方差为( ) A .6B .6C .66D .6.55.为了检查某超市货架上的奶粉是否含有三聚氰胺,要从编号依次为1到50的袋装奶粉中抽取5袋进行检验,用每部分选取的号码间隔一样的系统抽样方法确定所选取的5袋奶粉的编号可能是( ) A.5,10,15,20,25 B.2,4,8,16,32 C.1,2,3,4,5 D.7,17,27,37,476.(广州调研文、理)某校对全校男女学生共1600名进行健康调查,选用分层抽样法抽取一个容量为200的样本.已知女生比男生少抽了10人,则该校的女生人数应是 人.7. (韶关一模文、理)一个社会调查机构就某地居民的 月收入调查了10000人,并根据所得数据画了样本的频率分 布直方图(如下图)。
高中数学知识点精讲精析 线性回归分析 (2)
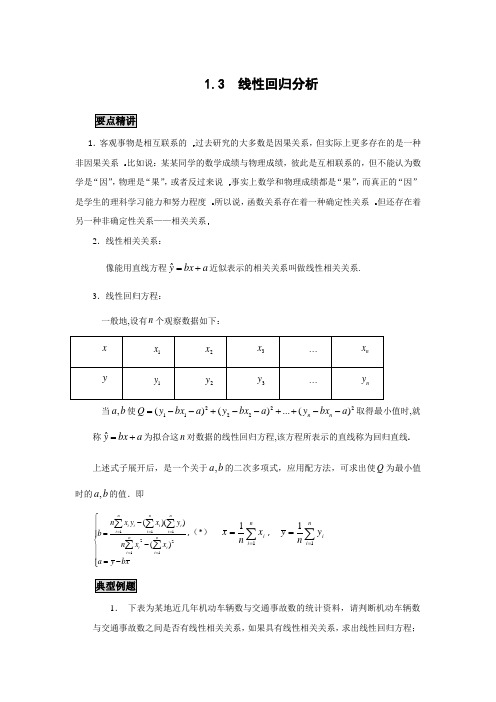
1.3 线性回归分析1.客观事物是相互联系的但实际上更多存在的是一种非因果关系 某某同学的数学成绩与物理成绩,彼此是互相联系的,但不能认为数学是“因”,物理是“果”,或者反过来说 “果”,而真正的“因”是学生的理科学习能力和努力程度 函数关系存在着一种确定性关系 2.线性相关关系:像能用直线方程ˆybx a =+近似表示的相关关系叫做线性相关关系. 3.线性回归方程:一般地,设有n 个观察数据如下:当,a b 使2221122()()...()n n Q y bx a y bx a y bx a =--+--++--取得最小值时,就称ˆybx a =+为拟合这n 对数据的线性回归方程,该方程所表示的直线称为回归直线. 上述式子展开后,是一个关于,a b 的二次多项式,应用配方法,可求出使Q 为最小值时的,a b 的值.即1112211()()()n n n i i i i i i i i i i i n x y x y b n x x a y bx=====⎧-⎪⎪=⎨-⎪⎪=-⎪⎩∑∑∑∑∑,(*) ∑==ni i x n x 11, ∑==n i i y n y 111. 下表为某地近几年机动车辆数与交通事故数的统计资料,请判断机动车辆数与交通事故数之间是否有线性相关关系,如果具有线性相关关系,求出线性回归方程;如果不具有线性相关关系,说明理由.【解析】在直角坐标系中画出数据的散点图,直观判断散点在一条直线附近,故具有线性相关关系.计算相应的数据之和:8888211111031,71.6,137835,9611.7ii i i i i i i i xy x x y ========∑∑∑∑,将它们代入(*)式计算得0.0774, 1.0241b a ≈=-,所以,所求线性回归方程为0.0774 1.0241y x =-.2.有10名同学高一(x )和高二(y )的数学成绩如下:⑴画出散点图;⑵求y 对x 的回归方程 【解析】 ⑴如图:⑵ 由已知表格的数据可得,,所以,又可查表中相应与显著性水平0.05和n -2的相关系数的临界值 因为可知,y 与x 具有相关关系. 因为y 与x 具有相关关系,设y=bx+a ,∴71,72.3x y ==101011710,723ii i i xy ====∑∑1010102211151467,50520,52541i ii i i i i x yx y ======∑∑∑10100.7802972i ix y x yr -⋅===∑0.050.632,r =0.05r r >1012110 1.22,14.3210i ii nii x y x yb a y bx xx==-⋅=≈=-≈--∑∑∴所求的回归方程为y=1.22x -14.32.3.下列两个变量之间的关系哪个不是函数关系( D ) A .角度和它的余弦值B.正方形边长和面积C .正n边形的边数和它的内角和 D.4.给出施化肥量对水稻产量影响的试验数据:(1)画出上表的散点图;(2)求出回归直线并且画出图形 【解析】(1)散点图(略).(2)表中的数据进行具体计算,列成以下表格 故可得到 2573075.43.399,75.430770002≈⨯-=≈⨯-=a b从而得回归直线方程是^4.75257y x =+.(图形略)5.一个工厂在某年里每月产品的总成本y (万元)与该月产量x (万件)之间由如下一组数据: 1)画出散点图;2)检验相关系数r 的显著性水平;3)求月总成本y 与月产量x 之间的回归直线方程.解析:=,==2.8475,=29.808,=99.2081,=54.243 1)画出散点图:2)r==在“相关系数检验的临界值表”查出与显著性水平0.05及自由度12-2=10相应的相关数临界值r0.05=0.576<0.997891, 这说明每月产品的总成本y(万元)与该月产量x(万件)之间存在线性相关关系。
(完整word版)多元线性回归模型案例分析

多元线性回归模型案例分析——中国人口自然增长分析一·研究目的要求中国从1971年开始全面开展了计划生育,使中国总和生育率很快从1970年的5.8降到1980年2.24,接近世代更替水平。
此后,人口自然增长率(即人口的生育率)很大程度上与经济的发展等各方面的因素相联系,与经济生活息息相关,为了研究此后影响中国人口自然增长的主要原因,分析全国人口增长规律,与猜测中国未来的增长趋势,需要建立计量经济学模型。
影响中国人口自然增长率的因素有很多,但据分析主要因素可能有:(1)从宏观经济上看,经济整体增长是人口自然增长的基本源泉;(2)居民消费水平,它的高低可能会间接影响人口增长率。
(3)文化程度,由于教育年限的高低,相应会转变人的传统观念,可能会间接影响人口自然增长率(4)人口分布,非农业与农业人口的比率也会对人口增长率有相应的影响。
二·模型设定为了全面反映中国“人口自然增长率”的全貌,选择人口增长率作为被解释变量,以反映中国人口的增长;选择“国名收入”及“人均GDP”作为经济整体增长的代表;选择“居民消费价格指数增长率”作为居民消费水平的代表。
暂不考虑文化程度及人口分布的影响。
从《中国统计年鉴》收集到以下数据(见表1):表1 中国人口增长率及相关数据设定的线性回归模型为:1222334t t t t t Y X X X u ββββ=++++三、估计参数利用EViews 估计模型的参数,方法是:1、建立工作文件:启动EViews ,点击File\New\Workfile ,在对话框“Workfile Range ”。
在“Workfile frequency ”中选择“Annual ” (年度),并在“Start date ”中输入开始时间“1988”,在“end date ”中输入最后时间“2005”,点击“ok ”,出现“Workfile UNTITLED ”工作框。
其中已有变量:“c ”—截距项 “resid ”—剩余项。
课件:Ch2 经典线性回归模型回顾之案例分析2(多元线性回归模型)

102.8153
0.1750
三、估计参数
模型估计的结果为:
Yˆi 2416.49 0.0112X2 0.0395X3 0.1460X4 22.8162X5 866.4100X6
(935.8816) (0.0018) (0.0080) (0.0517) (9.0867) (470.3214) t= (-2.5820) (6.3167) (4.9643) (2.8267) (2.5109) (1.8422) R 2 0.9679 , F=181.7539, n=31
验证理论
2
第五节 案例分析
研究的目的要求
为了研究影响中国地方财政教育支出差异的主要原因,分析地
方财政教育支出增长的数量规律,预测中国地方财政教育支出
的增长趋势,需要建立计量经济模型。
研究范围:2011年31个省市区的数据为样本 理论分析:影响中国地方财政教育支出的主要的因素有:
(1)由地区经济规模决定的地方整体财力;
0.1519
19669.56
6595.6
626.86
102.5655
0.1536
53210.28 10504.85
929.03
101.2925
0.1829
ห้องสมุดไป่ตู้
11720.87
4645
561.81
102.8054
0.1795
2522.66
877.34
565.08
100.8938
0.1634
10011.37
3593
722.92
102.8131
0.1784
内蒙古
390.69
14359.88
2481.71
线性回归经典假设的分析(案例)

线性回归经典假设的分析(案例)多重共线性分析财政收入是一个国家政府部门的公共收入。
国家财政收入的规模大小往往是衡量其经济实力的重要标志。
近20年来,我国财政收入一直保持着快速增长态势,经济总体发展良好。
一个国家财政收入的规模要受到经济规模等诸多因素的影响。
因此我们以财政收入为被解释变量,建立财政收入影响因素模型,分析影响财政收入的主要因素及其影响程度。
财政收入的因素众多复杂,但是通过研究经济理论对财政收入的解释以及对实践的考察,我们选取影响财政收入的因素为工业总产值、农业总产值、建筑业总产值、社会商品零售总产值、人口总数和受灾面积。
将这六个变量作为解释变量,财政收入作为被解释变量,利用1989~2003年数据建立中国国家财政收入计量经济模型,资料如下表。
表1 影响财政收入的因素资料(资料来源:《中国统计年鉴2004》)使用上述数据建立多元线性模型,采用普通最小二乘法得到国家财政收入估计方程为:1234562(0.46)(0.44)(8.59)(0.03)(3.80)(0.65)( 1.53)6922.5880.1260.9360.0400.5720.0920.0470.998620.56Y X X X X X X R F ---=-+-+++-==由上可以看出模型的拟合优度2R 和F 值都较大,说明建立的回归方程显著。
但在显著性水平为5%下, t (15)=2.131,大多数回归参数的t 检验不显著,若据此判断大部分因素对财政收入的影响不显著。
因此可以判定解释变量之间存在严重的多重共线性。
采用逐步回归法对解释变量进行筛选。
分别将Y 与各解释变量作一元线性回归方程,以拟合优度值最大的模型为基础,将其余变量依次引入方程中。
经过我们多次比较各模型的F 值和各参数的t 值,最终确定的模型为:242(1.79)(13.42)(35.57)519.6780.8120.7230.9971943.91Y X X R F -=-+==该模型的经济意义十分明显,即财政收入主要取决于农业总产值和社会商品零售总产值,各因素数量的变化引起财政收入总量变化的程度由各自的系数来反映。
第 2 讲(1) 一元线性、非线性回归分析

2
14
• 因此,点估计:
ˆ y ( x0 ) = a + bx0
• 区间估计:
ˆ y1 ( x0 ) = a + bx0 − δ ( x0 )
ˆ y 2 ( x0 ) = a + bx0 + δ ( x0 )
15
进似地, 很大( 进似地,当n很大(即 n → ∞ )时,t α 很大
α = 0.05
② 单侧控制
y < y,或 y < y 2
' 1 '
19
• 回归分析注意事项
(1)自变量、因变量的选择 )自变量、 (2)样本回归方程 ) (3)必须进行显著性检验 ) (4)任何回归方程都具有使用范围 )
20
二、一元非线性回归分析
1. 可化为线性回归的非线性回归
某石灰土强度与龄期关系 强度(Mpa Mpa) 2.5 2 1.5 1 0.5 0 0 50 100 150 200 龄期(d)
y1 < y < y2
' '
为此我们要合理控制x的取值,参照式(1)有下式:
P{
y1 < y < y2
' '
}≥ 1 − α
17
• 一般情况下可参照图求解:
′ y1 = a + bx −
t α ( n − 2 ) σˆ
2
1 (x − x )2 1 + + n L xx
′ y 2 = a + bx + t α
ˆ δ ( x0 ) ≈ 1.96σ
x0 又在 x 的平均值附近,取
= 1.96
2
ˆ ˆ y1 ( x0 ) ≈ a + bx0 − 1.96σ
第2讲线性回归案例分析

第2讲线性回归案例分析参与本讲的嘉宾主持人:各位老师大家好!欢迎大家继续参加我们模块三有关统计教学的讨论。
首先允许我来介绍一下请来的讨论的评论嘉宾,我身边这位是非常熟悉的首都师范大学张饴慈教授,这边是首都师范大学博士生导师王尚志教授,欢迎两位到场参加我们的讨论。
我们今天讨论的话题是统计学教学里面一个非常重要的内容。
我们标准里面提出来统计学内容在模块三里面是一个很重要的,实践性很强的内容,很多老师都做了一些专门的设计,提出来怎么学好统计,有一个很重要的思想,就是要通过活动课来学。
我们首先问王老师,活动在统计学学习里面有什么价值和作用?王尚志:统计学的教学或是概率统计或是必修三的教学,在标准上有一个特别建议,就要希望通过案例来进行教学。
就是希望通过具体的东西,让学生进行感悟,再逐渐上升成为对于这样一些统计、概率、算法的认识,我觉得这一点是特别重要的。
而案例教学对于统计这样特殊的课程来说,如果再赋予活动的内容,我想就更好了。
学生可以在做问题的过程中去体会,收集数据、怎么收集数据、怎么整理数据,怎么从数据中提取信息帮助我们说明问题这样一个过程。
根据我们的实践感觉这样的课如果加进去一些活动,会使我们学生通过自己的经历更好地展示,更好地理解他们要学习的内容。
张饴慈:我想统计这个课,在中学讲统计课不是从定义、总体、样本、众数,不是在这方面强调,而是希望他经历一个统计的整个过程,从开始的收集数据一直到最后得到结论,对结论的分析。
他有这个过程的话,对这个统计学的概念意义也能够很好的理解,而不是抽象的从一些定义、靠推理出发得到一些结论,跟那种还是不太一样的。
王尚志:另外在统计中应该更着重体现数学中的归纳的思想,我们要抽象地讲总体、抽样这些我想在中学层面上可能也很难讲得很清楚,包括在大学层面上可能也不一定能够讲清楚,可能更多的是现在在很多问题上,以及从专家上面还是有一些问题。
但是从处理数据这件事情,已经变成我们必须学习和理解的一个东西。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第2讲线性回归案例分析参与本讲的嘉宾主持人:各位老师大家好!欢迎大家继续参加我们模块三有关统计教学的讨论。
首先允许我来介绍一下请来的讨论的评论嘉宾,我身边这位是非常熟悉的首都师范大学张饴慈教授,这边是首都师范大学博士生导师王尚志教授,欢迎两位到场参加我们的讨论。
我们今天讨论的话题是统计学教学里面一个非常重要的内容。
我们标准里面提出来统计学内容在模块三里面是一个很重要的,实践性很强的内容,很多老师都做了一些专门的设计,提出来怎么学好统计,有一个很重要的思想,就是要通过活动课来学。
我们首先问王老师,活动在统计学学习里面有什么价值和作用?王尚志:统计学的教学或是概率统计或是必修三的教学,在标准上有一个特别建议,就要希望通过案例来进行教学。
就是希望通过具体的东西,让学生进行感悟,再逐渐上升成为对于这样一些统计、概率、算法的认识,我觉得这一点是特别重要的。
而案例教学对于统计这样特殊的课程来说,如果再赋予活动的内容,我想就更好了。
学生可以在做问题的过程中去体会,收集数据、怎么收集数据、怎么整理数据,怎么从数据中提取信息帮助我们说明问题这样一个过程。
根据我们的实践感觉这样的课如果加进去一些活动,会使我们学生通过自己的经历更好地展示,更好地理解他们要学习的内容。
张饴慈:我想统计这个课,在中学讲统计课不是从定义、总体、样本、众数,不是在这方面强调,而是希望他经历一个统计的整个过程,从开始的收集数据一直到最后得到结论,对结论的分析。
他有这个过程的话,对这个统计学的概念意义也能够很好的理解,而不是抽象的从一些定义、靠推理出发得到一些结论,跟那种还是不太一样的。
王尚志:另外在统计中应该更着重体现数学中的归纳的思想,我们要抽象地讲总体、抽样这些我想在中学层面上可能也很难讲得很清楚,包括在大学层面上可能也不一定能够讲清楚,可能更多的是现在在很多问题上,以及从专家上面还是有一些问题。
但是从处理数据这件事情,已经变成我们必须学习和理解的一个东西。
所以我想通过活动第一能吸引学生,学生愿意做,比如流行歌的变化趋势,结婚年龄的变化趋势,学生很感兴趣,首先问题就抓住他们,然后通过分组大家合作,一起来收集数据,一起整理数据,一起从数据中提取信息说明问题。
我想这个过程对统计学的学习是非常重要的,而且也是能够调动我们学生积极性的一个非常好的一种创意。
主持人:我觉得老师们都提得很清楚,这个活动的价值不仅有助于学习数学,学习统计,理解这个内容,而且是一个过程,积累这方面经验的过程。
我想结合我这个课给老师们谈一点想法,首先要做好这样的活动课的核心,是要有一个核心问题,问题的产生有两种方式,一种比较容易控制。
就像用用课本上现有的例子让学生实践一遍这个最容易还有一种是老师提出具体的问题,用这种方式提出两个例子。
第一个问题就是做一个人口,给学生一个实际问题。
比如2008年中国18岁的人口,给这个人口数一个估计。
王尚志:我想你要是估计2010年更好?主持人:我们要今年就这么出了,今年18岁的人口就这么问,当年留这个问题学生认为好象这个事情没有当做是一个统计学的认识,认为这个是找个公式算算,根据什么算?不知道,那就查书,老师没有给,就去找问题源最后发现上网说老师我要真的直接查出来,我说那也算得到结果。
大家一查没有结果,没有这个结果是两种一种是中国经济年鉴上面对这个数据是收费、保密;有一个测算的结果,常规的结果只有哪年做的统计、人口普查有这个数据。
学生认为没有就说老师好像你给得条件不够,你总得给我们点什么?但是经过查了以后,他说没有是一个检查的结果,但是他有一些别的查出来了。
比如说15亿说人口预计估计是15亿,有了这个结果同学就觉得那好办了,有很多同学提出一些想法,有些同学还有查平均寿命,中国人73岁。
把15亿除以73就认为是18岁人口,当然老师看了这个数据的时候,不是表态,大家参与这个过程,要说对还是不对,有人说这个不对?为什么不对其实问一个技术的问题,如果18岁人口是15除以73再乘以15亿,就会出这样一个问题就是一个分布积累。
我问1岁的人或者74岁的人,学生马上就找我说,老师这个不应该是这样,应该是前面多一点后面少一点,但是不知道多多少。
到这儿讨论就进了一步,知道这个分布肯定是这么下降,那怎么办呢再放开,就是这个过程要让同学体会结果再说大家再想办法的时候,这个办法是隔了三天再讨论的时候又有新的办法,最有意思的是一个同学说,我妈妈告诉我我们这个楼有188个人,其中有3个人是18岁,然后就是188分之3,乘以15亿,这个结果又进了一步。
但是大家又开始争论,凭什么拿你这个楼的数据,有的同学很恶劣或者很有意思问,你们家住哪儿?是不是一个老年公寓,18岁的人少,或者是一个青年公寓代表性不好,大家又进一步讨论到代表性,什么叫好的代表性数据,要抽出代表性好的数据。
大家再想办法,于是就有各种各样的办法,其中有的家长是劳改局的局长,把监狱里18岁的犯人人数抽出来,这也有问题,男性、女性犯罪率也不一样,级别每一年也是不一样的。
王尚志:犯罪也不是平均分配,不均匀。
主持人:但是最后有的同学说,他抽他们家乡福建省他有有一个数据,这个代表性就比较好一点。
但是不管怎么说,这个讨论结果,大家对于抽样的质量、抽样的代表性有了更深刻的认识。
这种过程一直做下去的时候,我们把这个过程拖得比较长,但是最后大家得到一个感觉,把这个问题解决过程中,对于样本、估计总体、对于数据的代表性,对于一个好的抽样,对于分层抽样、还有随机抽样,这些概念都慢慢进行复习,我觉得这个过程可能对学生学习统计是很需要的过程。
王尚志:思明这个做法,我知道。
他刚才讲得这个过程,老师一定会提出一些置疑,一会儿收集这个,一会儿收集那个,这个课怎么安排?我记得思明是这么操作这件事的,在每一课的前五分钟左右的时间讨论这个统计问题,讨论出一点结论就打住进入这个课的学习,既调动了学生的学习热情,又进行了统计课的进展,我觉得一举两得,把课上和课下结合起来,把几节课结合起来,因为都是学生参与的,所以学生做这些问题一般比较兴奋,所以我觉得这是挺好的一个创意。
主持人:因为这个问题,统计学开始不是特别明显,后面做了一个问题,是学生反给我的一个问题,我们觉得全班都可以一直做。
全班同学都有学英语的电子词典,电子词典大家就比谁得好?一开始比价钱,800元、1000元、500元,还有比名牌,突然学生提出一个质量标准。
其实一个好的词典有两种,一种是含得词库大,解释丰富,有原文的解释,我们就统一说你能不能告诉我们你拿的电子词典里面有多少单词?这个问题大家就说没有什么可做的,看看说明书就行,我们有一款说明书上面标记出来说它有40万英文单词,这是我们首先说的,做40万的单词是可能达到一个超级大的字库,是不是真使这样?我们提出这样的问题,大家觉得这是一个统计学的问题,我们就拨下去,大家帮我们验证手里有的电子词典,真实的词库有多大?这个问题宏观的学生能平行能提出好几个问题,我的单词量是什么样?国家规定高中毕业生应该达到5000-6000,我到没到?一个英语专业的毕业生在二年级时应该到8000,他怎么来测算自己?都是这样的问题,结果我们就小组讨论,大家针对同一个问题用课题研究的方法,大家先来一起做,说怎么解决个问题?那就要抽样,先要把单词的分布说清楚。
A打头、B打头,26个字母各自打头单词分布是多少?同学们就提了很多办法,比如查字典,看字典的页数比,A有多厚,这是一个挺好的办法,再返回来在字典上挑最短,比如V打头的单词最少,按出来,VO更少,就把这个东西弄出来根据它的分布,测算出整个词典的库容是多少?最后这个库容做出来之后,发现基本上有一半的字典都是虚库容,一般学生用的字典也就是6-10万左右。
在这个过程中,对大家的影响就是统计学很有用,统计学的方法在这个过程大家都做了一次实践,甚至大家提到了平行横向,比如减少测量误差,减少统计学误差,挑字典就不能挑化工字典,医学医药字典,要挑通用字典,很多很多这样的思想就对统计学的工作的过程有一个更深的理解。
王尚志:找问题我觉得是我们老师面临的一个挑战性问题。
刚才思明说,一个班可以选择共同的问题大家一起来做,也有的老师允许学生去找问题。
我也给大家补充一个故事,北京市8中前几年的一个故事,一个小女孩,她们家住一个宿舍,门口有一个老太太,这个老太太生活也很可怜,儿子不孝顺,没人养活她,所以老太太不得不在宿舍门口摆一个摊儿,就卖杂物,特别是卖雪糕、冰淇淋、牛奶这些东西。
这个小孩非常有同情心,她很希望帮助这个老太太,但是这个老太太又希望自食其力,这个小姑娘想我怎么帮助她?于是她就发现老太太面临着一个主要的问题,就是每一天进货的数量是多少?我想我们都可以明白,如果进货的数量过大而卖不出去就有可能坏掉。
如果你进货量不够,而买的人又多,你又赚不了这个钱,于是这个小孩就想用自己学得统计学办法来解决这个问题,她用两个星期的时间每天请很多人帮忙来记录购买各种不同饮料的情况或者冰淇淋的情况,这就是所谓的抽样,然后进行统计,最后计算出一个结果,提出一个方案告诉老太太,比如说牛奶要进多少?什么牌子的进多少?雪糕什么牌子进多少?老太太很不相信这个小孩,就不愿意用她这个方案?这个小孩就说服了她妈妈,说我做得这个是很有道理的,一定能让老太太能够增加收入最后小孩的妈妈找到这个老太太,说您就用她这个方案,如果亏了我来补这个钱,后来老太太被母女俩的行为很感动,就开始使用小孩提出这样的一个统计方案。
结果老太太比原来多赚了一些钱,老太太非常高兴,这个同学也非常高兴。
就在我们这个活动中报告了她的结果,我想这些都是很有个性的问题。
我觉得不是没有问题,我们身边有大量的统计学的问题,可供学生选择,它们是非常有吸引力的问题,又是学生力所能及能够解决的问题。
所以我们希望我们的老师可以让我们的学生从他们的身边发现一些统计问题,或者通过小组合作的方式完成这些统计问题,他们在这个过程中能更好地学习统计学。
张饴慈:这里我还想谈一谈,统计教学对我们高中的老师来说也是一个挑战,现在我去听了一些课,发现老师对这些问题缺乏意识,或者老是那几个问题,课本上的问题,书本上的问题很难举出自己的问题例子。
所以我觉得刚才王老师还有张思明老师说了,实际上有很多问题,我想对老师来说,首先在自己上要有心观察这些问题,要有问题意识,这是一非常重要的事。
其次的活,现在在一些地方,比如北京积累了一批的案例,拿这些案例做参考,我觉得也是一个不错的方法,另外最好能把这些题目让学生看一看,学生有很大的积极性,学生能够提出非常多的案例。
甚至有一些案例老师都不敢做,都觉得这能不能做,我不懂?甚至会有这样的情况,我认为这是非常好的现象,利用别人的资源充分发挥学生,自己做一个有心人,我想这样就能把问题越来越能找到,就能找到一些适合中学生做的案例。
