自动控制原理第2章
合集下载
《自动控制原理》第2章 线性系统的传递函数

+
anc(t)
=
b0
dm dtm
r(t)
+
b1
d m−1 d t m −1
r(t)
++
bm−1
d dt
r(t)
+
bmr(t)
(m n)
设r(t), c(t)及各阶导数在t=0时的值均为零(零初始条件), 则对方程两端求拉氏变换,可得系统的传递函数
Ch2 控制系统的数学模型
◼ 传递函数的一般形式:
Ch2 控制系统的数学模型
第二章 控制系统的数学模型
Ch2 控制系统的数学模型
本章内容
❖ 引言 ❖ 物理系统的微分方程 ❖ 拉氏变换与拉氏反变换 ❖ 线性系统的传递函数 ❖ 方框图及其等效变换 ❖ 信号流图与Mason公式*
Ch2 控制系统的数学模型
2.3 线性系统的传递函数
一. 传递函数的定义
Ux(s) =
I
(s) − I2(s) sC1
(2)
I 2 (s)
=
Ux
(s) −Uo(s) R2
(3)
U o (s)
=
I 2 (s) sC2
(4)
Ch2 控制系统的数学模型
I (s) = Ui (s) −U x (s) (1) R1
Ui _
I
1/R1
Ux
Ux(s) =
I
(s) − I2(s) sC1
Uo (s)
Ui (s) (b)
I(s) Uo (s)
Ch2 控制系统的数学模型
I(s)
(c)
Uo (s)
Ui (s)
I(s)
- Uo (s) (d)
自动控制原理-第二章-控制系统的数学模型—结构图-信号流图-传递函数

(1)单位脉冲 (2)单位阶跃 (3)单位斜坡 (4)单位加速度 (5)指数函数 (6)正弦函数 (7)余弦函数
f (t)
(t)
1(t )
t t2 2
e at
sin t cos t
F (s)
1
1s 1 s2 1 s3
1 (s a)
(s2 2) s (s2 2)
2.2 线性定常微分方程的求解 拉普拉斯反变换:部分分式展开法
时域 差分方程
解析式模型
状态方程
复域
传递函数 结构图-信号流图
图模型
频域 频率特性
数学模型是一个反应变量之间关系的表达式,在不同的域中有不同的表现形式!
1.引言
解析法:依据系统及元件各变量之间所遵循的物理、化学定律列写出变量间的数学表 达式,并实验验证。
实验法:对系统或元件输入一定形式的信号(例如阶跃信号、单位脉冲信号、正弦信 号等),根据系统或元件的输出响应,经过数据处理而辨识出系统的数学模型。
k 1 v n1
s
l 1 n2
(Ti s 1)
(T
2 j
s2
2Tj
s
1)
i 1
j 1
适用于 频域分
析
3.2 传递函数的基本概念 传递函数的标准形式
K:增益
K*=根轨迹增益
K与K*的关系:
两者关系
m
zj
K K*
j 1 n
pi
i 1
3.3 典型环节及其传递函数
一个传递函数可以分解为若干个基本因子的乘积,每个基本因子就称为典型环节。常见 的几种形式有:
Y (s)
R(s)
Y (s)
f (t)
(t)
1(t )
t t2 2
e at
sin t cos t
F (s)
1
1s 1 s2 1 s3
1 (s a)
(s2 2) s (s2 2)
2.2 线性定常微分方程的求解 拉普拉斯反变换:部分分式展开法
时域 差分方程
解析式模型
状态方程
复域
传递函数 结构图-信号流图
图模型
频域 频率特性
数学模型是一个反应变量之间关系的表达式,在不同的域中有不同的表现形式!
1.引言
解析法:依据系统及元件各变量之间所遵循的物理、化学定律列写出变量间的数学表 达式,并实验验证。
实验法:对系统或元件输入一定形式的信号(例如阶跃信号、单位脉冲信号、正弦信 号等),根据系统或元件的输出响应,经过数据处理而辨识出系统的数学模型。
k 1 v n1
s
l 1 n2
(Ti s 1)
(T
2 j
s2
2Tj
s
1)
i 1
j 1
适用于 频域分
析
3.2 传递函数的基本概念 传递函数的标准形式
K:增益
K*=根轨迹增益
K与K*的关系:
两者关系
m
zj
K K*
j 1 n
pi
i 1
3.3 典型环节及其传递函数
一个传递函数可以分解为若干个基本因子的乘积,每个基本因子就称为典型环节。常见 的几种形式有:
Y (s)
R(s)
Y (s)
自动控制原理:第二章--控制系统数学模型全

TaTLma KJe K
dMdML m dtdt
L
Tm
Ra J K eKm
——机电时间常数(秒);
Ta
La Ra
—电动机电枢回路时间常数 (秒)
若输出为电动机的转角q ,则有
TaTm
d 3q
dt 3
Tm
d 2q
dt 2
dq
dt
1 Ke
ua
Tm J
ML
TaTm J
dM L dt
—— 三阶线性定常微分方程 9
(1)根据克希霍夫定律可写出原始方程式
((23))式消LuLCcdd中去(titd)i中2d是utRc间2(中Cti1)变间C1量iR变dCti量idd后udt,ct,(t它)u输r与u(入tc输)(输t)出出uu微rc((tt)分)有方如程下式关系
或
T1T2
d 2uc (t) dt 2
T2
duc (t) dt
扰动输入为负载转矩ML。 (1)列各元件方程式。电动机方程式为:
TaTm
d 2w
dt 2
测输T速Km出发td为d电wt电测压机速w 反 K馈1e系ua数
Tm J
M反L馈 电TaJT压m
dM L dt
ua Kae ut Ktw e ur ut 12
(2)消去中间变量。从以上各式中消去中间变
量ua,e,ut,最后得到系统的微分方程式
线性(或线性化)定常系统在零初始条件下, 输出量的拉氏变换与输入量的拉氏变换之比 称为传递函数。
令线C性(s定)=常L[c系(t统)],由R下(s)述=Ln阶[r(微t)]分,方在程初描始述条:件为零
时[[aab,nnmbssdmdn进mt+ndn+dt行acmmbn(tm拉-r1)-(s1t氏ns)-am1变n+-1b1+…m换dd…1t+,nndd+1a1t得mm1bcs1(11到+ts)r+a关(t0b)]于0C]的RD(sM的s的a(()分s1s(分))=代sdbd为母)t1子为数cd传d多(tt多传方)r递项(项t程递函)式a式0函数c。b(0数tr) (t)
自动控制原理-第二章 控制系统的数学模型

dn dtn f ( t )
t
f (t)dt 0
t
f ( )d
n
ki .L[ f (t )]
i 1
sF (s) f (0 )
s2F (s) sf (0 ) f (0 )
snF (s) sn1 f (0 ) sn2 f (0 ) f (n1) (0 )
电枢回路方程为
La
dia (t) dt
Raia (t)
Ea (t)
ua (t)
电磁转矩方程 M m Cmia (t)
电动机轴上转矩平衡方程
Jm
dm (t)
dt
fmm (t)
Mm
MC
(t)
若以角速度 m 为输出量、电枢电压 ua 为输入量,
消去中间变量,直流电动机的微分方程为
(s2+s+1)Uc(s)= Ur(s)+0.1(s+2)
即 U S 1 U S 0.1S 2
C
S2 S 1 r
S2 S 1
通电瞬间, ur(t)=1 或 Ur(s)=L[ur(t)]=1/S
故 U S 1 1 0.1S 2
C
S2 S 1 S S2 S 1
再对上式两边求反拉氏变换:
u c
t
L1 U C
S
L1
S
2
1 S
1
1 S
S
2
1 S
1
=1+1.15e-0.5tSin(0.866t-120°)+ 0.2e-0.5tSin(0.866t+30°)
t
f (t)dt 0
t
f ( )d
n
ki .L[ f (t )]
i 1
sF (s) f (0 )
s2F (s) sf (0 ) f (0 )
snF (s) sn1 f (0 ) sn2 f (0 ) f (n1) (0 )
电枢回路方程为
La
dia (t) dt
Raia (t)
Ea (t)
ua (t)
电磁转矩方程 M m Cmia (t)
电动机轴上转矩平衡方程
Jm
dm (t)
dt
fmm (t)
Mm
MC
(t)
若以角速度 m 为输出量、电枢电压 ua 为输入量,
消去中间变量,直流电动机的微分方程为
(s2+s+1)Uc(s)= Ur(s)+0.1(s+2)
即 U S 1 U S 0.1S 2
C
S2 S 1 r
S2 S 1
通电瞬间, ur(t)=1 或 Ur(s)=L[ur(t)]=1/S
故 U S 1 1 0.1S 2
C
S2 S 1 S S2 S 1
再对上式两边求反拉氏变换:
u c
t
L1 U C
S
L1
S
2
1 S
1
1 S
S
2
1 S
1
=1+1.15e-0.5tSin(0.866t-120°)+ 0.2e-0.5tSin(0.866t+30°)
自动控制原理第2章
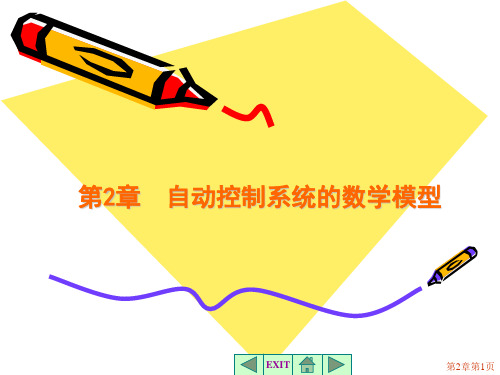
略去高次项,
yy0 dfd(IT
第2章第20页
② 两个自变量
y=f(r1, r2)
静态工作点: y0=f(r10, r20)
在y0=f(r10, r20) 附近展开成泰勒级数,即
y
f
(r10,r20)rf1
(r1
r10)rf2
(r2
r20)
EXIT
第2章第14页
2.1.3 机电系统
图示为一他激直流电动机。 +
图中,ω为电动机角速度
( rad/s ) , Mc 为 折 算 到 电 ua 动机轴上的总负载力矩 _
( N·m ) , ua 为 电 枢 电 压 + (V)。设激磁电流恒定,
并忽略电枢反应。
_
ia La
ea Ra
Mc
负载
取得u: a为给定输入量, ω为输出量,Mc为扰动量,忽略电枢电感,
• 传递函数是在拉氏变换基础之上引入的描述线性定常系统或 元件输入、输出关系的函数。它是和微分方程一一对应的一 种数学模型,它能方便地分析系统或元件结构参数对系统响 应的影响。
EXIT
第2章第26页
1. 定义 零初始条件下,线性定常系统输出量的拉氏变
换与输入量的拉氏变换之比,称为该系统的传递函 数,记为G(s),即:
例 一个由弹簧-质量-阻尼器组成 的机械平移系统如图所示。m为物 体质量,k为弹簧系数,f 为粘性 阻尼系数,外力F(t)为输入量,位 移x(t)为输出量。列写系统的运动 方程。
F
k
m x
EXIT
第2章第10页
解 在物体受外力F的作用下,质量m相对于初始状态的位移、速 度、加速度分别为x、dx/dt、d2x/dt2 。设外作用力F为输入量,位 移 x 为输出量。根据弹簧、质量、阻尼器上力与位移、速度的关 系和牛顿第二定律,可列出作用在上的力和加速度之间的关系为
自动控制原理第2版全篇

=
△
- + - 其中:△称为系统特征式 △= 1 ∑La ∑LbLc ∑LdLeLf+…
—∑La 所有单独回路增益之和
∑L∑和dLLebLLf—c—所有所三有个互两不两接互触回不路接增益触乘回积路之增和益乘积之
Pk—从R(s)到C(s)的第k条前向通路传递函数
△k称为第k条前向通路的余子式 去掉第k条前向通路后所求的△
x0
(x x0 )
1 d 2 f (x)
2!
dx2
x0
(x x0 )2
忽略二阶以上各项,可写成
y
f
(x0 )
df (x)
dx x0
(x
x0 )
2、对于具有两个自变量的非线性函数,设输入 量 为x1(t)和x2(t) ,输出量为y(t) ,系统正常工作 点为y0= f(x10, x20) 。
注意:相加点和分支点一般不能变位
25
2.3.3闭环传递函数
1、给定输入单独作用下的系统闭环传递函数
(s) G1G2 G1G2 1 G1G2H 1 Gk
2、扰动输入单独作用下的闭环系统
n
(
s)
1
G2 G1G2
H
G2 1 Gk
3、误差传递函数:误差信号的拉氏变换与输入信 号的拉氏变换之比。
(1)给定输入单独作用下的闭环系统
Er
(
s)
1
1 G1G2
H
1 1 Gk
(2)扰动输入单独作用下的闭环系统
En
(
s)
1
G2 H G1G2
H
G2H 1 Gk
4)给定输入和扰动输入作用下的闭环系统的总的输
出量和偏差输出量
自动控制原理第2章

传递函数是在拉氏变换基础上的复域中的数学模型。
※传递函数不仅可以表征系统的动态特性,而且可以
用来研究系统的结构或参数变化对系统性能的影响。
微分方程 t (时域)
L
L
1
F
F 1
系统
传递函数
s j
j
频率特性
s
(复域)
s
(频域)
2.3.1拉氏变换相关知识
2.3.2传递函数的定义
线性定常系统在零初始条件下,输出量的拉氏变换
②两个自变量: y=f(x1, x2) 静态工作点: y0=f(x10, x20) 在y0=f(x10, x20) 附近展开成泰勒级数,即
f 1 2 f f 2 f 2 f 2 ( x1 x10 ) 2 y f ( x10 , x20 ) ( x1 x10 ) ( x2 x20 ) ( x1 x10 )(x2 x20 ) 2 ( x2 x20 ) 2 x 2! x x2 x1x2 x2 1 1
例2.5试建立如图2.4所示系 统的微分方程。
R1
解:根据克希霍夫电压定律, 可写出下列方程组
u1
R2
ur
i1
C1 图2.4
i2
C2
uc
1 ur R1i1 C (i1 i2 )dt 1 1 1 (i1 i2 )dt R2i2 i2 dt C2 C1 1 uc i2 dt C2
用台劳级数展开为
df ( x) 1 d 2 f ( x) y f ( x) f ( x0 ) ( ) x 0 ( x x0 ) ( ) x 0 ( x x0 ) 2 ... dx 2! dx 2
※传递函数不仅可以表征系统的动态特性,而且可以
用来研究系统的结构或参数变化对系统性能的影响。
微分方程 t (时域)
L
L
1
F
F 1
系统
传递函数
s j
j
频率特性
s
(复域)
s
(频域)
2.3.1拉氏变换相关知识
2.3.2传递函数的定义
线性定常系统在零初始条件下,输出量的拉氏变换
②两个自变量: y=f(x1, x2) 静态工作点: y0=f(x10, x20) 在y0=f(x10, x20) 附近展开成泰勒级数,即
f 1 2 f f 2 f 2 f 2 ( x1 x10 ) 2 y f ( x10 , x20 ) ( x1 x10 ) ( x2 x20 ) ( x1 x10 )(x2 x20 ) 2 ( x2 x20 ) 2 x 2! x x2 x1x2 x2 1 1
例2.5试建立如图2.4所示系 统的微分方程。
R1
解:根据克希霍夫电压定律, 可写出下列方程组
u1
R2
ur
i1
C1 图2.4
i2
C2
uc
1 ur R1i1 C (i1 i2 )dt 1 1 1 (i1 i2 )dt R2i2 i2 dt C2 C1 1 uc i2 dt C2
用台劳级数展开为
df ( x) 1 d 2 f ( x) y f ( x) f ( x0 ) ( ) x 0 ( x x0 ) ( ) x 0 ( x x0 ) 2 ... dx 2! dx 2
自动控制原理:第2章-控制系统的数学模型可编辑全文

下图所示为三个环节串联的例子。图中,每个环节的方框图为:
*
上式表明,三个环节的串联可以用一个等效环节来代替。这种情况可以推广到有限个环节串联(各环节之间无负载效应)的情况,等效环节的传递函数等于各个串联环节的传递函数的乘积,如有n个环节串联则等效传递函数可表示为:
*
2. 环节的并联
环节并联的特点是各环节的输入信号相同,输出信号相加(或相减)。
2.7 闭环系统的传递函数
一.闭环系统
*
(3)开环传递函数: 假设N(s)=0,主反馈信号B(s)与误差信号E(s)之比。
(2)反馈回路传递函数:假设N(s)=0,主反馈信号B(s)与输出信号C(s)之比。
*
(4)闭环传递函数 Closed-loop Transfer Function 假设N(s)=0 输出信号C(s)与输入信号R(s)之比。
复习拉普拉斯变换有关内容(6)
(3)积分定理
零初始条件下有:
进一步有:
例4 求 L[t]=?
解.
例5 求
解.
复习拉普拉斯变换有关内容(7)
(4)实位移定理
证明:
例6
解:
令
复习拉普拉斯变换有关内容(8)
(5)复位移定理
证明:
令
例7
例8
例9
复习拉普拉斯变换有关内容(9)
负反馈:反馈信号与给定输入信号符号相反的反馈。
正反馈:反馈信号与给定输入信号符号相同的反馈。
*
上述三种基本变换是进行方框图等效变换的基础。对于较复杂的系统,例如当系统具有信号交叉或反馈环交叉时,仅靠这三种方法是不够的。
(二)信号相加点和信号分支点的等效变换
对于一般系统的方框图,系统中常常出现信号或反馈环相互交叉的现象,此时可将信号相加点(汇合点)或信号分支点(引出点)作适当的等效移动,先消除各种形式的交叉,再进行等效变换即可。
*
上式表明,三个环节的串联可以用一个等效环节来代替。这种情况可以推广到有限个环节串联(各环节之间无负载效应)的情况,等效环节的传递函数等于各个串联环节的传递函数的乘积,如有n个环节串联则等效传递函数可表示为:
*
2. 环节的并联
环节并联的特点是各环节的输入信号相同,输出信号相加(或相减)。
2.7 闭环系统的传递函数
一.闭环系统
*
(3)开环传递函数: 假设N(s)=0,主反馈信号B(s)与误差信号E(s)之比。
(2)反馈回路传递函数:假设N(s)=0,主反馈信号B(s)与输出信号C(s)之比。
*
(4)闭环传递函数 Closed-loop Transfer Function 假设N(s)=0 输出信号C(s)与输入信号R(s)之比。
复习拉普拉斯变换有关内容(6)
(3)积分定理
零初始条件下有:
进一步有:
例4 求 L[t]=?
解.
例5 求
解.
复习拉普拉斯变换有关内容(7)
(4)实位移定理
证明:
例6
解:
令
复习拉普拉斯变换有关内容(8)
(5)复位移定理
证明:
令
例7
例8
例9
复习拉普拉斯变换有关内容(9)
负反馈:反馈信号与给定输入信号符号相反的反馈。
正反馈:反馈信号与给定输入信号符号相同的反馈。
*
上述三种基本变换是进行方框图等效变换的基础。对于较复杂的系统,例如当系统具有信号交叉或反馈环交叉时,仅靠这三种方法是不够的。
(二)信号相加点和信号分支点的等效变换
对于一般系统的方框图,系统中常常出现信号或反馈环相互交叉的现象,此时可将信号相加点(汇合点)或信号分支点(引出点)作适当的等效移动,先消除各种形式的交叉,再进行等效变换即可。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
放大器
比较器
' f
u f K a e
测速发电机 ut Kt w
e=ur-ut ,因为Δur =0 ,故 e ut 消去中间变量,得扰动输入ΔML下的线性化方程:
2 d 3w dw ' d w TM TaT TM (Ta T f ) (T f' TM K t K a K mTa ) (1 K )w 3 2 dt dt dt 2 Ra C f ia 0 TM ' d M L ' dM L [TaT f (Ta T f ) M L ], Km R K ' F 2 f a 0 J dt dt
d 2 u c (t ) du c (t ) LC RC u c (t ) u r (t ) 2 dt dt 2 d u c (t ) du c (t ) T1T2 T2 u c (t ) u r (t ) 或 2 dt dt
(线性定常二阶微分方程式)
自动控制原理
5
举例2
弹簧—质量—阻尼器系统
自动控制原理
4
2.2.1 典型控制系统举例
举例1 R-L-C电路
要求:列出uc(t)与ur(t)的关系方程式 (1)根据克希霍夫定律可写出原始方程式 di 1 1 L Ri idt ur (t ) , u c (t ) idt dt C C (2)消去中间变量i后,得输入输出微分方程式
(2)Md和ia是中间变量。由于电动机转矩与电枢电流和气 隙磁通的乘积成正比,又因磁通恒定,有M d K m ia , 联立求解,整理后得
L a J d 2w Ra J dw Ra La dM L 1 w ua ML K e K m dt 2 K e K m dt Ke Ke Km K e K m dt
Ra J Tm K eK m
Ta La Ra
——机电时间常数(秒) ——电动机电枢回路时间常数(秒) ,
一般比Tm小 若输出为电动机轴的转角q ,则有
Ta Tm d 3q dt 3 Tm d 2q dt 2 T T T dM L dq 1 ua m M L a m dt Ke J J dt
自动控制原理
3
2.2 控制系统微分方程的建立
建立系统(或部件)微分方程式的一般步骤:
(1)在条件许可下,适当简化,忽略一些次要因素; (2)根据物理或化学定律,列出部件的原始方程式; (3)列出原始方程式中中间变量与其它变量的关系式; (4)从所有方程式中消去中间变量,仅保留系统的输入变量和 输出变量; (5)最后,将微分方程表示成标准形式,即输出变量在左,输 入变量在右,导数阶次从高到低排列。
自动控制原理7来自(续上页)L a J d 2w Ra J dw Ra La dM L 1 w ua ML 2 K e K m dt K e K m dt Ke Ke Km K e K m dt
或
Ta Tm
d 2w dt 2
Tm
T T T dM L dw 1 w ua m M L a m dt Ke J J dt
L f J d w L f J dw K ( ) w i uf R f B dt 2 R f B dt Rf B
2
d
f f
或
T f Tm
d 2w dt 2
(T f Tm )
dw w Kdu f dt
9
自动控制原理
举例5
电动机转速控制系统
电动机转速控制系统原理图及结构图 w为输出,ur为参考输入,ML为扰动输入 (1)列各部件方程式: T T dM L Tm d 2w dw 1 TaTm 2 Tm w ua a m ML
M d 2 y (t ) B dy(t ) 1 y (t ) f (t ) 2 K dt K dt K
(线性定常二阶微分方程式)
自动控制原理
6
举例3
电枢控制的直流电动机
电枢电压控制的直流电动机线路原理图和结构图 输入—电枢电压ua 输出—轴角位移q 或角速度w 扰动—负载转矩ML
dia (1)列写原始方程式。电枢回路方程式:La dt Ra i K ew ua dw J 根据刚体旋转定律,写出运动方程式: dt M L M d
(三阶线性定常微分方程)
自动控制原理
8
举例4
磁场控制的直流电动机
设电枢电流Ia=常数,气隙磁通F(t) Kf if (t),激磁回路 电感Lf为常值。 d (1)激磁回路方程式: u f R f i f
dt
(2)转矩平衡方程式: J dw Bw M d dt Φ (3)消去中间变量, M : L i ,M d Km Km K f i f Kii f
令C(s)=L[c(t)],R(s)=L[r(t)],在初始条件为零时,进行拉氏变换, 可得到s的代数方程
s n a1s n 1 an 1s an C s b0 s m b1s m 1 bm 1s bm R s
dt di La a Ra ia K eFw u(非线性方程) a dt dw ' J M L M D, M D K M F i(非线性方程) a dt
u f Ka e
ut Ktw
e ur ut
自动控制原理
12
2.2.2 非线性微分方程的线性化(续)
设的工作点为0 ,if 的工作点为if0 ,在工作点的邻域内, 对if的各阶导数存在,它可展开成泰勒级数:
自动控制原理
11
2.2.2 非线性微分方程的线性化
直流电动机转速自动镇定系统图
设各处信号(变量)均在工作点附近不大范围内变动。列原始方程 d (1) 激磁回路 (与if是非线性关系) Rf if u f (2) 电枢回路 (3) 电动机 (4) 放大器 (5) 测速发电机 (6) 比较器
要求:写出系统在外力f (t)作用下的运动方程式
(1)列出原始方程式。根据牛顿第二定律, 有 (2)消去中间变量
f1 (t ) B dy(t ) dt
d2 y f (t ) f1 (t ) f 2 (t ) M 2 dt
B—— 阻尼系数 K—— 弹性系数
f2 (t) = Ky(t) 代入上式并整理
bm 称为传递系数(或静态放大系数)。 an
(6)一个传递函数只能表示一个输入对一个输出的函数关系。
17
2.3.1 典型环节及其传递函数
(1)比例环节 G(s)= K
d 1 d 2 1 d n 0 ( ) 0 i f ( 2 ) 0 (i f ) 2 ( n ) 0 (i f ) n Rn1 di f 2! di f n! di f
与if是之间的非线性关系
忽略二次以上高次项,得: d d 0 ( ) 0 i f 0 L' f i f ( ) 0 tan L' f , , di f di f 写成偏量线性化方程式: L ' f i f
自动控制原理
14
2.3
2.3.1 传递函数的概念
传递函数
RC电路如下:根据克希霍夫定律, 可列写微分方程
Ri(t ) uc (t ) ur (t )
1 uc (t ) i(t )dt C duc (t ) RC uc (t ) u r (t ) 消去中间变量i(t),得 dt RCsUc (s) RCuc (0) U c (s) U r (s) 对上式进行拉氏变换 1 RC U c ( s) U r ( s) uc (0) 求出Uc(s)的表达式 RCs 1 RCs 1 1 U c ( s) U r ( s) 若uc(0)=0 RCs 1 U c ( s) 1 1 或 G( s) 式中 T=RC U r ( s) RCs 1 Ts 1
dt dt
ua Kae,
ut Ktw,
Ke
J
dt
J
e ur ut
(2)消去中间变量,得: K K K T T dM L Tm d 2w dw TaTm 2 Tm (1 K )w a ur a m M L,K a t dt dt Ke J dt J Ke
自动控制原理
线性定常系统的传递函数为
C (s) bm s m bm1 s m1 b1 s b0 M (s) G( s) n n 1 R(s) a n s a n1 s a1 s a0 D( s )
自动控制原理
16
2.3.1 传递函数的性质
(1)传递函数是复变量s的有理真分式函数,分子的阶数m一 般低于或等于分母的阶数n, 即m≤n ,且所有系数均为 实数。 (2)传递函数只取决于系统和元件的结构和参数,与外作用 及初始条件无关。 (3)一定的传递函数有一定的零、极点分布图与之对应,因 此传递函数的零、极点分布图也表征了系统的动态性能。 (4) 若下式中s = 0,则G (0)
C (s) b0 s m b1s m1 bm1s bm M (s) G( s ) n n 1 R( s ) s a1s an1s an D(s) (5) 传递函数只能表示输入与输出的函数关系,至于系统中 的中间变量无法反映出来。
自动控制原理
' f
所以激磁回路偏量线性化方程为:T
自动控制原理
di f dt
i f
1 u f Rf
13
2.2.2非线性微分方程的线性化(续)
同理,设各处信号(变量)均在工作点附近不大范围内变动, 它们的偏量方程式可求之如下:
电枢回路 电动机
La dia Ra ia K e' w 0 F K e'F0 w 0 dt dw ' J M L K M (F0 ia ia 0 F ) , F C f i f dt
