交错级数及其判别法
合集下载
交错级数与任意项级数
n
2n
2 n1
(3) {S }单调有界则收敛。 2n
证: (1) 先证{S }收敛。 2n S2n (u1 u2 ) (u3 u4 ) (u2n1 u2n ) S2n u1 (u2 u3) (u4 u5 ) (u2n2 u2n1) u2n 是单调递增有界数列, 故
(2) 再证{S }收敛于S。 2 n1
n1
( )n
ns
收敛， n1(ns)n绝对收敛.
(2)当 1时,
n1
( )n
ns
发散，
(3)当 1时, n1(n1s)n 交错级数，
s 1, 绝对收敛.
n1(ns)n 发散.
1 s 0, 条件收敛.
思考： 下列命题是否正确.
#2014022506
对一个收敛级数的和s来说它是无穷多个数的“和”， 也可以按照有限个数求和的运算规律进行，比如可 以交换各项的顺序。
(2n
1
2)2
a2n2
Lebnitze条件是充分的不是必要的
判别下列级数收敛的是:
1) 1 1 1 1 (1)n1 1
234
n
#2014022503
2) 1 1 1 1 (1)n1 1
2! 3! 4!
n!
3)
1 10
2 102
3 103
4 104
(1)n1
n 10n
判别下列级数各项取绝对值后级数收敛的是: #2014022504
（A）正确
（B）不正确
（C）不确定
绝对收敛级数与条件收敛级数的区别.
*定理8..
设pn
un
2
un
, qn
un
2
un
02-交错级数及其审敛法PPT
一、交错级数及其审敛法
定义：正、负项相间的级数称为交错级数，即
8
8
£ (~1)n an，或 £(-1)-1 an，
n=1
n=1
其中对任意n,有an > 0 .
交错级数审敛法(莱布尼茨判别法):
8
若交错级数£ (-1)"T an (匕> 0)的一般项满足：
n=1
① an+i < an (n = L2,…)；
(ii) lim an = 0 .
nT8 8
£ 则⑴ (-1)n-1 an收敛,且其和s满足：0 < s < a1;
n=1
(2)级数的余项rn = s-sn满足|rn| < an+1.
板书少 证明：⑴..・an_1 - an > 0,
•・• s2 n = （a1 一 a2）+ （a3 一 a4）+ …+ （a2 n-1 一 a 2 n）
数列｛ s2〃｝是单调增加的,
又 s2n = a1 一 （a2 一 a3）-----（a2n-2 一 a2n-1）
一 a2n
< "数列｛S2n ｝是有界的，
lim s2n = s < a1. •/ lim a2n+1 = 0,
n—8
n—B
板 书，・・・ lim 5+i = lim(sn + a2w+1) = s,
竺"ns ns
・级数收敛于和S, 且s < a1.
(2)余项 rn =~(an+1 - an+2 + …)， + rn\ = an+1 - an+2 …，
满足收敛的两个条件，...|" < an+!•
定义：正、负项相间的级数称为交错级数，即
8
8
£ (~1)n an，或 £(-1)-1 an，
n=1
n=1
其中对任意n,有an > 0 .
交错级数审敛法(莱布尼茨判别法):
8
若交错级数£ (-1)"T an (匕> 0)的一般项满足：
n=1
① an+i < an (n = L2,…)；
(ii) lim an = 0 .
nT8 8
£ 则⑴ (-1)n-1 an收敛,且其和s满足：0 < s < a1;
n=1
(2)级数的余项rn = s-sn满足|rn| < an+1.
板书少 证明：⑴..・an_1 - an > 0,
•・• s2 n = （a1 一 a2）+ （a3 一 a4）+ …+ （a2 n-1 一 a 2 n）
数列｛ s2〃｝是单调增加的,
又 s2n = a1 一 （a2 一 a3）-----（a2n-2 一 a2n-1）
一 a2n
< "数列｛S2n ｝是有界的，
lim s2n = s < a1. •/ lim a2n+1 = 0,
n—8
n—B
板 书，・・・ lim 5+i = lim(sn + a2w+1) = s,
竺"ns ns
・级数收敛于和S, 且s < a1.
(2)余项 rn =~(an+1 - an+2 + …)， + rn\ = an+1 - an+2 …，
满足收敛的两个条件，...|" < an+!•
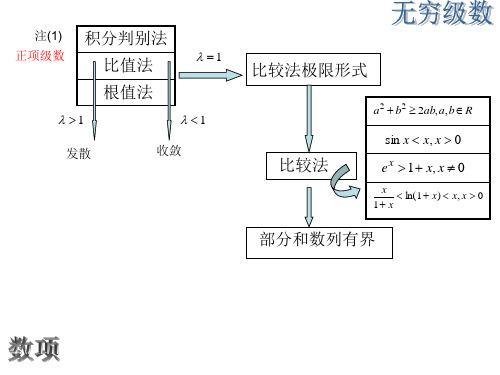
一般级数的审敛法
1 单减, 在 (1,+) 上单增, 即 x ln x 1 故 当 n 1 时单减, n ln n
1 1 un un+1 ( n 1), n ln n ( n + 1) ln( n + 1)
所以此交错级数收敛， 故原级数是条件收敛．
定理 如果任意项级数
n 1
则任意重排得到的级数也绝对收敛,且有相同的 和数. 注:由条件收敛级数重排得到的新级数,即使收敛 也不一定收敛于原来的和数,而且条件收敛收敛 级数适当重排后,可得到发散级数,或收敛于任何 事先指定的数.如： 1 1 1 1 1 n +1 1 ( 1) 1 + + + A n 2 3 4 5 6 n 1 1 1 1 1 1 3 n+1 1 ( 1) 1+ + + + A n 3 2 5 7 4 2 n 1
lim u2 n+1 0,
n
lim s2 n s u1 .
lim s2 n+1 lim( s2 n + u2 n+1 ) s,
n n
级数收敛于和s, 且s u1 .
余项 rn (un+1 un+ 2 + L),
rn un+1 un+ 2 + L,
n 1 n 1 n 1
sin n 例 3 判别级数 2 的收敛性. n 1 n
解
sin n 1 1 2 2 , 而 2 收敛, n1 n n n
sin n 2 收敛, n n1
故由定理知原级数收敛.
级数收敛的判别技巧
级数收敛的判别技巧级数是数学中一个重要的概念，它是由一系列数相加而成的。
在数学中，我们经常需要判断一个级数是否收敛，即求出它的和。
本文将介绍几种常用的级数收敛的判别技巧。
一、正项级数的判别法正项级数是指级数的每一项都是非负数的情况。
对于正项级数，我们可以使用以下几种方法来判断其是否收敛。
1. 比较判别法比较判别法是最常用的判别法之一。
它的基本思想是将待判别的级数与一个已知的级数进行比较，通过比较它们的大小关系来判断级数的收敛性。
比较判别法分为两种情况：（1）若存在一个收敛的级数∑an，使得对于所有的n，都有an≤bn，则待判别的级数∑bn也收敛。
（2）若存在一个发散的级数∑an，使得对于所有的n，都有an≥bn，则待判别的级数∑bn也发散。
2. 比值判别法比值判别法是判别正项级数收敛性的常用方法之一。
它的基本思想是通过计算级数相邻两项的比值的极限来判断级数的收敛性。
具体步骤如下：（1）计算级数相邻两项的比值：rn=an+1/an。
（2）求出极限limn→∞rn。
（3）根据极限的大小判断级数的收敛性：- 若0≤limn→∞rn<1，则级数收敛；- 若limn→∞rn>1，则级数发散；- 若limn→∞rn=1，则判别不出级数的收敛性，需要使用其他方法进行判别。
3. 根值判别法根值判别法也是判别正项级数收敛性的常用方法之一。
它的基本思想是通过计算级数项的根号的极限来判断级数的收敛性。
具体步骤如下：（1）计算级数项的根号：rn=(an)^(1/n)。
（2）求出极限limn→∞rn。
（3）根据极限的大小判断级数的收敛性：- 若0≤limn→∞rn<1，则级数收敛；- 若limn→∞rn>1，则级数发散；- 若limn→∞rn=1，则判别不出级数的收敛性，需要使用其他方法进行判别。
二、任意项级数的判别法任意项级数是指级数的每一项都可以是正数、负数或零的情况。
对于任意项级数，我们可以使用以下几种方法来判断其是否收敛。
任意项级数
（2）一般说来，如果 ∑ | un |发散，我们不能断定 ∑ un
n =1 n =1 ∞ ∞
也发散。
但用比值 （或根值） 判别法， 判断级数 ∑ | un |发散，
n =1 ∞
则我们就能断定 ∑ un 也发散。
n=1
∞
机动
目录
上页
下页
返回
结束
定理 3：比值判别法(达朗贝尔判别法)：
un+1 设 un 是任意项级数,且 lim = ρ ，则 n→ ∞ u n n =1 （1）ρ < 1时级数绝对收敛；
n =1 n =1 n =1
机动 目录 上页 下页 返回 结束
∞
∞
n =1 ∞
n =1 ∞
n =1 ∞
sin n 例 3：判别级数 ∑ 的收敛性。 2 n =1 n
解
∞ sin n 1 1 Q 2 ≤ 2 , 而 ∑ 2 收敛 , n n n =1 n
∞
sin n ∴ ∑ 2 收敛 , n =1 n
说明: 本题的方法是常用的方法。
机动
目录
上页
下页
返回
结束
( −1) | an | 例9： 设级数 ∑ a 收敛，讨论级数 ∑ n2 + λ n =1 n =1 的收敛性 (其中λ为常数 ，λ > 0)
n 2 n
∞
∞
解：
| an | 1 2 1 ≤ ( an + 2 ) 级数绝对收敛 2 n +λ n +λ 2
返回
结束
an 例 8：若级数 ∑ an 收敛，则级数 ∑ 绝对收敛。 n =1 n =1 n
2
∞
∞
证:
an 1 1 1 2 | | = | an | ≤ ( 2 + an ) n n 2 n 1 因为 ∑ 2 和 n =1 n
n =1 n =1 ∞ ∞
也发散。
但用比值 （或根值） 判别法， 判断级数 ∑ | un |发散，
n =1 ∞
则我们就能断定 ∑ un 也发散。
n=1
∞
机动
目录
上页
下页
返回
结束
定理 3：比值判别法(达朗贝尔判别法)：
un+1 设 un 是任意项级数,且 lim = ρ ，则 n→ ∞ u n n =1 （1）ρ < 1时级数绝对收敛；
n =1 n =1 n =1
机动 目录 上页 下页 返回 结束
∞
∞
n =1 ∞
n =1 ∞
n =1 ∞
sin n 例 3：判别级数 ∑ 的收敛性。 2 n =1 n
解
∞ sin n 1 1 Q 2 ≤ 2 , 而 ∑ 2 收敛 , n n n =1 n
∞
sin n ∴ ∑ 2 收敛 , n =1 n
说明: 本题的方法是常用的方法。
机动
目录
上页
下页
返回
结束
( −1) | an | 例9： 设级数 ∑ a 收敛，讨论级数 ∑ n2 + λ n =1 n =1 的收敛性 (其中λ为常数 ，λ > 0)
n 2 n
∞
∞
解：
| an | 1 2 1 ≤ ( an + 2 ) 级数绝对收敛 2 n +λ n +λ 2
返回
结束
an 例 8：若级数 ∑ an 收敛，则级数 ∑ 绝对收敛。 n =1 n =1 n
2
∞
∞
证:
an 1 1 1 2 | | = | an | ≤ ( 2 + an ) n n 2 n 1 因为 ∑ 2 和 n =1 n
交错级数及其判别法
进一步开拓交错级数在其他领域的应 用，如生物学、经济学、社会学等。
加强交叉学科的合作研究
鼓励数学与其他学科的交叉合作研究， 共同探索交错级数在解决实际问题中 的应用。
感谢您的观看
THANKS
交错级数的项必须满足单调递减的条件，即每一项都小于或等于前一项。
交错级数收敛的充分条件
当交错级数的公比q满足$|q| < 1$时，级数收敛。
交错级数收敛的证明方法
数学归纳法
通过数学归纳法证明交错级数的每一项 都小于或等于前一项，从而证明级数收 敛。
VS
比较判别法
将交错级数与已知收敛的等比级数进行比 较，利用等比级数的性质判断交错级数的 收敛性。
在工程中的应用
01
02
03
信号处理
在信号处理中，交错级数 被用来分析和处理各种信 号，如音频、图像等。
控制系统
在控制系统中，交错级数 被用来描述和设计各种控 制算法和系统。
工程优化
在工程优化中，交错级数 被用来求解各种优化问题， 如结构优化、路径规划等。
05
交错级数的扩展与展望
交错级数的扩展研究
交错级数收敛的实例
莱布尼茨级数
$1 - frac{1}{3} + frac{1}{5} - frac{1}{7} + cdots$是一个典型的交错级数，它满足单调 递减的条件且公比$q = -frac{2}{3}$满足$|q| < 1$，因此该级数收敛。
调和级数
$1 + frac{1}{2} + frac{1}{3} + frac{1}{4} + cdots$是一个非交错的调和级数，不满足 单调递减的条件，因此该级数发散。
加强交叉学科的合作研究
鼓励数学与其他学科的交叉合作研究， 共同探索交错级数在解决实际问题中 的应用。
感谢您的观看
THANKS
交错级数的项必须满足单调递减的条件，即每一项都小于或等于前一项。
交错级数收敛的充分条件
当交错级数的公比q满足$|q| < 1$时，级数收敛。
交错级数收敛的证明方法
数学归纳法
通过数学归纳法证明交错级数的每一项 都小于或等于前一项，从而证明级数收 敛。
VS
比较判别法
将交错级数与已知收敛的等比级数进行比 较，利用等比级数的性质判断交错级数的 收敛性。
在工程中的应用
01
02
03
信号处理
在信号处理中，交错级数 被用来分析和处理各种信 号，如音频、图像等。
控制系统
在控制系统中，交错级数 被用来描述和设计各种控 制算法和系统。
工程优化
在工程优化中，交错级数 被用来求解各种优化问题， 如结构优化、路径规划等。
05
交错级数的扩展与展望
交错级数的扩展研究
交错级数收敛的实例
莱布尼茨级数
$1 - frac{1}{3} + frac{1}{5} - frac{1}{7} + cdots$是一个典型的交错级数，它满足单调 递减的条件且公比$q = -frac{2}{3}$满足$|q| < 1$，因此该级数收敛。
调和级数
$1 + frac{1}{2} + frac{1}{3} + frac{1}{4} + cdots$是一个非交错的调和级数，不满足 单调递减的条件，因此该级数发散。
浅谈交错级数敛散性的判定
浅谈交错级数敛散性的判定
交错级数是一种特殊的无穷级数。
在交错级数中，每一项的符号需要交替出现。
即正负交替，或者负正交替。
例如，交错级数$$\sum_{n=1}^{\infty}(-
1)^n\frac{1}{n}=\frac{1}{1}-\frac{1}{2}+\frac{1}{3}-
\frac{1}{4}+\cdots$$
交错级数的判定方法分为三种：莱布尼茨判别法、比较判别法和积分判别法。
1.莱布尼茨判别法
对于一个交错级数$$\sum_{n=1}^{\infty}(-1)^na_n$$
如果该级数满足以下两个条件，则级数收敛：
（1）$a_n>0$；
（2）$a_n$单调递减，即$a_n>a_{n+1}$。
这个判别法不适用于非交错级数。
2.比较判别法
对于一个交错级数$$\sum_{n=1}^{\infty}(-1)^na_n$$
如果$|a_{n+1}|<|a_n|$，则级数收敛。
如果$|a_{n+1}|\geq|a_n|$，则级数发散。
3.积分判别法
对于一个交错级数$$\sum_{n=1}^{\infty}(-1)^na_n$$ 如果$\int_{1}^{\infty}|a(x)|dx$收敛，则级数收敛。
如果$\int_{1}^{\infty}|a(x)|dx$发散，则级数发散。
交错级数敛散性判别法
00
:例7判断级数勺敛散性，若收敛，指出是绝对收敛还是条件收敛?
解lim un+l
n—8 un
=lim
MT8
xn+1 n n+1 xn
=|x|
|X| < 1时，级数〉绝对收敛;
ixi > 1时，级数2 :发散；
V^00 vn X =1时，级数〉，发散；
V^00 vn
=T时，级数）土条件收敛.
X
^n=l n
定理若交错级数2：二(一1)”—侦如，un > 0, (n = L 2,…)满足
(1)"孔 2 Un+dO = 1, 2,…)；
(2) limun = 0.
71—00
贝U级数U攵敛， 旦其禾口s三 , 其余项I—兀| < 以兀+■•
证明取交错交错级数前2m项之和
Szm = “1 — “2 + “3 — “4 +----!" u2m-l _ u2m —("1 一 “2)+(“3 一 “4)----!■ (u2m-l 一 u2m)
(2)当I > 1 (或I = oo)时，级数竺u兀发散;
(3)当I =丄时，级数、言旨“兀的敛散性不能判别.
♦ 例5判断级数2：］苧*］敛散性.
P > 1时，级数5 绝对收敛； »n=l n
00 ( 一 1
0<p< 1时，级数〉 条件收敛; 厶」71 = 1 n
P < 0时，级数发散
（_1）"一12
moo lUTOO
综上所述，UmSn = S,级数收敛，且S V ”1. n—>oo
余项|R兀 I = Un + 1 — (Un+2 — U兀+3)—…< Un+r.
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
这些乘积 uiv j 可以按各种方法排成不同的级数， 常用的有按正方形顺序或按对角线顺序依次相 加，于是分别有：
u1v1 u1v2 u2v2 u2v1 u1v3 u2v3 u3v3 和 u1v1 u1v2 u2v1 u1v3 u2v2 u3v1
§3 一般项级数
一、交错级数及其判别法
定义: 正、负项相间的级数
u1 u2 u3 u4 1n1un (un 0, n 1,2, ),
(1)
u n1 n
为交错级数
收敛
定理12.11（莱布尼茨判别法）设
(1)
u n1 n
满足以下两个条件
1）数列 un 单调递减
u1 数列 s2n是有界的 ,
lim n
s2n
s
u1 .
lim
n
u2n1
0,
lim n
s2n1
lim(
n
s2n
u2n1 )
s,
所以数列 Sn 收敛
推论 若级数
(1)
u n1 n
满足莱布尼茨判别法的条件，则收敛级数
(1)
u n1 n
lim un1 lim 0
n un
n n 1
所以对所考察的级数对任何实数 级数都绝对收敛
，
绝对收敛级数的两个重要性质
1. 级数的重排
定义:把正整数列{1,2, ,n } 到它自身的一一映射
f : n k(n) 称为正整数列的重排,相应地对于数列
{un} 按映射 F : un uk(n) 所得到的数列 {uk(n)}称为原
vn v1 v2 vn B (2)
为收敛级数，他（1）与（2）中每一项所有 可能的乘积列成下表：
u1v1 u1v2 u2v1 u2v2 u3v1 u3v2
u1v3 u2v3 u3v3
u1vn u2vn u3vn
unv1 unv2 unv3 unvn
级数的重排,相应也称级数 uk(n)是级数 un 的
n 1
n 1
重排.
定理12.13 设级数 un 绝对收敛,且其和等于 S n 1
则任意重排得到的级数也绝对收敛,且有相同的
和数.
注:由条件收敛级数重排得到的新级数,即使收敛
也不一定收敛于原来的和数,而且条件收敛收敛
级数适当重排后,可得到发散级数,或收敛于任何
n
| kvk || (1 2 )1 (2 3) 2 (n1 n ) n1 n n | k 1 | (1 2 ) (n1 n ) | A | n |
A | 1 n | A | n |
推论 （阿贝耳引理）若
（1） 1,2 , ,n 是单调数组；
（2）对任一正整数 k(1 k n) 有 | k | A, 则记
n
max{| k
k
|} 时，有：|
k vk
k 1
|
3A
证：由（1）知 1 2,2 3, ,n1 n 都是
同号的，于是由分部求和公式及条件（2）推得
事先指定的数.如：
(1)n1 1 1 1 1 1 1 1 A
n1
n 23456
(1)n1 1 1 1 1 1 1 1 3 A
n1
n 32574
2
2. 级数的乘积
设 un u1 u2 un A (1)
证 对任何正数
总存在正数N，使得n>N和任意正数r,有
um1 um2 umr
由于
r
因此由柯西准则知级数 un 也是收敛的。
例1 证明级数
an n! 绝对收敛 .
证 由于对任何实数 有
的余项估计式为
Rn un1
对于级数
() n1 , n
(1) n1 n
10 n 根 据
莱布尼茨判别法易知都是收敛
的。
二、绝对收敛与条件收敛
若级数 un 收敛，则称级数 un 绝对收敛
若级数 un 收敛，但是级数 un 不收敛，则称级数
un 为条件收敛。
定理12.12 若级数 un 收敛，则级数 un 收敛
实数，若令 k v1 v2 vk (k 1,2, , n)
则有如下分部求和公式成立：
n
ivi (1 2 )1 (2 3) 2 (n1 n ) n1 n n
i1
证：以 v1 1,vk k k1 (k 2,3, , n) 分别乘以 k (k 2,3, , n), 整理后就得所要证的公式。
2）lim n
u
0
则
(1)
u n1 n
证明 un1 un 0, s2n (u1 u2 ) (u3 u4 ) (u2n1 u2n )
数列 s2n是单调增加的 , 又 s2n u1 (u2 u3 ) (u2n2 u2n1 ) u2n
定理12.14 (柯西定理) 若级数(1)、（2）都绝对
收敛，则对（3）中所有乘积 uiv j 按任意顺序排列
所得到的级数 wn也绝对收敛，且其和等于AB. n 1
例2
等比级数
1
r n1
1 r n1
r ＜1 是绝对收敛的，将
按 r n 2
u1v1 u1v2 u2v1 u1v3 u2v2 u3v3
的顺序排列，则得到
1 1 (r r) (r 2 r 2 r 2 ) r n r n r n
(1 r)2
=1+2r 3r 2 (n 1)r n
三、阿贝耳判别法和狄利克雷判别法
引理（分部求和公式）设 i ,vi (i 1,2, , n) 为两组