最新第二章被控对象的特性
被控对象特性
令ΔQ1=q1，ΔQ2=q2
d h c q1 - q 2 dt S
H Q2 R2
流出量的变化量ΔQ2与水位的变化量ΔH成正比，与流出阀门2的阻力R2 成反比,即
即
hc q2 R2
假定水位变化不大，则R2可近似认为是一个常数
hc Kll 0 dhc q1 - q 2 R2 dt S S
dhc hc S Kll 0 dt R2
dhc R2 hc KlR 2 l 0 dt
令
T SR 2 K 0 K lR 2
T——对象的时间常数 K0——对象的控制通道放大系数
可写成下列形式
dhc T hc K 0 l 0 dt
这是水箱在阶跃扰动下的微分方程，特解（t=0）是
一阶被控干扰控制通道的动态方程为：
Tf
有纯滞后
Tf
Tc , Tf , Kc , K f
q(t ), f (t ), y(t )
分别为控制通道、扰动通道的时间常数和放大系数； 分别为操纵变量，扰动变量，被控变量。
二阶微分方程
二阶被控过程控制通道的动态方程为：
d 2 yt dy(t ) Tc1Tc 2 (Tc1 Tc 2 ) y (t ) K c q(t ) 2 dt dt
2.1 被控对象特性
2.1.1被控对象特性定义
被控对象特性是指被控过程的输入变量 （操纵变量或干扰变量）发生变化时，其 输出变量（被控变量）随时间的变化规律。
控制通道定义
所谓通道是输入变量对输出变量的作用途径，被控变量受到操纵变量和干扰变量 的共同作用影响。因此其特性分为被控变量随操纵变量的变化规律和随干扰变量 的变化规律。
控制阀等的安装位置与对象本身之间总有一段距离，输入量 （或输出量）的改变和信息的传递均需要时间。
第2章 被控对象的特性
10
举例
一个对象如果可以用一个一阶微分方程式来描 述其特性（通常称一阶对象），则可表示为
a1yt a0 yt xt
（2-2）
或表示成 Tyt yt Kxt
（2-3）
式中
T a1 , K 1
a0
a0
上式中的系数与对象的特性有关，一般需要通过对象 的内部机理分析或大量的实验数据处理得到。
2020年7月10日星期五 2时9分7秒
衡。 水槽 对象
例如水槽对象
稳定时Q1＝Q2，h保持稳定。如Q1突 然增加，h逐渐增加，由于h↑，Q2随液 体静压强↑而↑，Q1与Q2的差值逐渐减小， h↑减慢，最后Q1与Q2重新相等， h又自 行稳定在新的高度h/上.
有自衡的对象有利于控制。除部分反 应器、锅炉汽包、泵排液对象之外，大 多数有自衡性质。
湖北大学化学化工学院 杨世芳
8
(2)参量模型
当数学模型是采用数学方程式来描述时，称为参量模 型。对象的参量模型可以用描述对象输入、输出关系的微 分方程式、偏微分方程式、状态方程、差分方程等形式来 表示。
2020年7月10日星期五 2时9分5秒
湖北大学化学化工学院 杨世芳
9
对于线性的集中参数对象
通常可用常系数线性微分方程式来描述方程式来描述
当数学模型是采用曲线或数据表格等来表示时，称为 非参量模型。非参量模型可以通过记录实验结果来得到， 有时也可以通过计算来得到。
特点
形象、清晰，比较容易看出其定性的特征
缺点 直接利用它们来进行系统的分析和设计往往比较困难
表达形式 对象在一定形式输入作用下的输出曲线或数据来表示
2020年7月10日星期五 2时9分5秒
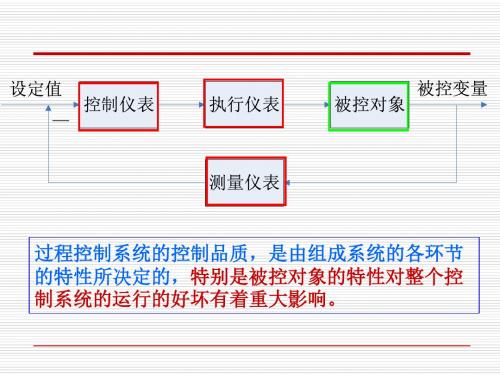
自动控制系统是由被控对象、测量变送装置、控
第2章 被控对象
RC[sU o (s) Uo (0)] Uo (s) Ui (s)
在零初始条件下
1 U o ( s) U i ( s) RCs 1 1 ui (t )为单位阶跃信号，则 L[ui (t )] s
1 1 RC U o ( s) s( RCs 1) s( s 1 ) RC 利用部分分式展开
C1 C2 U o ( s) s (s 1 ) RC 1
C1 RC s s 0 1 1 s( s ) RC 1 1 RC C2 (s ) 1 1 RC s 1 s(s ) RC RC
1 1 U o ( s) s (s 1 ) RC 对上式左右两边进行拉氏反变换
2
2
s1, 2 n n 2 1
当阻尼比 不同时，特征根有不同的形式，使得其系统响 应的形式也不同。
①当 1 时，特征根为一对不相等负实根 ，系统为过阻 尼系统，单位阶跃响应为单调上升曲线。 ②当 1 时，特征根为一对相等负实根 ，系统为临界阻 尼系统，单位阶跃响应为单调上升曲线，但快速性好于 过阻尼系统。 ③当 0 1 时，特征根为一对带负实部的共轭复数根 ， 系统为欠阻尼系统，单位阶跃响应为衰减振荡曲线。 ④当 0 时，特征根为一对共轭虚根 ，系统为无阻尼系 统，单位阶跃响应为等幅振荡曲线。 ⑤当 0 时，特征根在s复平面的右半平面，系统单位阶 跃响应是发散曲线。
（2）峰值时间 tp
取第一周期 k = 1
（3）超调量 Mp
因为
（4）调节时间 ts 由指数函数包络线求得。 由
由于
包络线
2.2 被控对象实例
电枢电压控制的他励直流电动机，是控制系统中常用 的执行机构或被控对象。当电枢电压 ud 发生变化时，其转 速 n 及转角 ɵ 产生相应的变化。 （1）确定输入量和输出量。 取输入量为电动机的电枢电压
自动控制原理第二章复习总结（第二版）
⾃动控制原理第⼆章复习总结（第⼆版）第⼆章过程装备控制基础本章内容：简单过程控制系统的设计复杂控制系统的结构、特点及应⽤。
第⼀节被控对象的特性⼀、被控对象的数学描述（⼀）单容液位对象1．有⾃衡特性的单容对象2．⽆⾃衡特性的单容对象（⼆）双容液位对象1．典型结构：双容⽔槽如图2-5所⽰。
图2-5 双容液位对象图2-6 ⼆阶对象特性曲线2．平衡关系：⽔槽1的动态平衡关系为：3．⼆阶被控对象：1222122221)(Q K h dt dh T T dt h d T T ?=+++式（2-18）就是描述图2-5所⽰双容⽔槽被控对象的⼆阶微分⽅程式。
称⼆阶被控对象。
⼆、被控对象的特性参数（⼀）放⼤系数K（⼜称静态增益）（⼆）时间常数T（三）滞后时间τ（1）．传递滞后τ0（或纯滞后）：（2）．容量滞后τc可知τ=τ0+τc。
三、对象特性的实验测定对象特性的求取⽅法通常有两种：1．数学⽅法2．实验测定法（⼀）响应曲线法：（⼆）脉冲响应法第⼆节单回路控制系统定义：（⼜称简单控制系统），是指由⼀个被控对象、⼀个检测元件及变送器、⼀个调节器和⼀个执⾏器所构成的闭合系统。
⼀、单回路控制系统的设计设计步骤：1．了解被控对象2．了解被控对象的动静态特性及⼯艺过程、设备等3．确定控制⽅案4．整定调节器的参数（⼀）被控变量的选择（⼆）操纵变量的选择（三）检测变送环节的影响（四）执⾏器的影响⼆、调节器的调节规律1．概念调节器的输出信号随输⼊信号变化的规律。
2．类型位式、⽐例、积分、微分。
（⼀）位式调节规律1．双位调节2．具有中间区的双位调节3．其他三位或更多位的调节。
（⼆）⽐例调节规律（P ）1．⽐例放⼤倍数（K ）2．⽐例度δ3．⽐例度对过渡过程的影响（如图2-24所⽰）4．调节作⽤⽐例调节能较为迅速地克服⼲扰的影响，使系统很快地稳定下来。
通常适⽤于⼲扰少扰动幅度⼩、符合变化不⼤、滞后较⼩或者控制精度要求不⾼的场合。
（三）⽐例积分调节规律（PI ）1．积分调节规律（I ）（1）概念：调节器输出信号的变化量与输⼊偏差的积分成正⽐==?t I t I dt t e T dt t e K t u 00)(1)()(式中：K I 为积分速度，T I 为积分时间。
第2章 被控对象的特性
将式（2-13）和式（2-14）代入式（2-15）式（2-16）
中得
A1dh1/dt=Qi-h1/R1
(2-17)
A2dh2/dt=h1/R1- h2/R2
(2-18)
将式（2-17）与式（2-18）相加，并整理后得
d h1
dt
1 (Q Ai
1
A2
dh2
dt
h2 ) R2
（2-19）
将式（2-18）求导，得
2
(T
1
T
)
2
dh
dt
2
h
2
KQ
i
（2-22）
上式为一个二阶常系数微分方程式。式中 T1,T2 分别为两个水槽的时间常数， K为整个对象的放大系 数。
三、纯滞后对象的数学模型及特性 在连续化生产中，有的被控对象或过程，在输
入变量发生变化后，输出变量并不立刻随之变化， 而是要隔上一段时间后才产生响应。我们把具有这 种特性的对象称为纯滞后对象。
s
i
Q Q VQ
0
s
0
将这些变量代入式（2-1）中，就可得到
A dVh VQ VQ
dt
i
o
（2-2）
在上式中，还不能清楚地看出h与Qi的关系。因为 式中有QO的存在，为此，必须将QO从式中消除。由工 艺设备的特性可知，QO与h 的关系是非线性的。考虑 到h和QO的变化量相对较小，可以近似认为QO与h 成正 比，与出水阀的阻力系数R 成反比，其具体关系式如
(1）对象输出的变化特点 对式（2-9）求导，可得h在t时刻变化速度，即
e dVh KVQ t /T
dt
T
当t=0时，得h的初始变化速度
（2-10）
控制对象的动态特性及其传递函数的求取(两点法、切线法)资料
容量迟延时间τC
多容有自平衡对象可用下列传递函 数表示：
2.无自平衡能力多容对象
自平衡单容对象
无平衡单容对象
无自平衡能力多容对象
μ
Kμ Q0 _
1 h1 1
F1 S
R1
Q1
1 h2
F2 S
自平衡单容对象
无平衡单容对象
阶跃响应
特征参数
多容无自平衡能力的对象的动态特性 可用两组参数描述：
Ta、 和 、
积分时间越大，被调量(输出)的变 化越慢，输出对输入的反应越慢
特征参数
(2)飞升速度ε
dh dt
t0
K
1
0 F Ta
传递函数可以写作：
H(s) 1
(s) S Ta S
积分环节
0
t0 h
0
t
特征参数
（3）自平衡率ρ
∵在无自平衡能力单容对象中其流出侧阻力Rs＝∞
∴其自平衡率为：
单容被控对象的动态特性
单容被控对象：
是指只有一个贮存物质或能量的容积。这 种对象用一阶微分方程式来描述。单容被控对 象可分为有自平衡单容对象和无自平衡单容对 象两大类 。
1.有自平衡的单容对象
μ 1 k
Q1
h
F
2
Rs
Q2
说明：
1. 被控对象受到扰动后平衡被破坏， 不需外来的调节作用，而依靠被调 量自身变化使对象重新恢复平衡的 特性，称为对象的自平衡特性。
a
控制阀 中间阀 流出阀
特征参数
多容有自平衡能力的对象的动态特性
可用两组三个参数描述即 ：
容积迟延时间τC 、时间常数TC及放大系数K
第2章 控制对象的动态特性
1
dh dt t 0
dh ( )max / 0 dt K 0 T K 0 0 T
能源与动力工程学院
小 结
综上所述，有自平衡能力的单容被控对象的动态特 性可以用两组4个参数描述，它们之间的关系为：
K 0 1 K 时间常数：T＝ dh dt t 0 h 1 放大系数：K 0 0 1 自平衡率：＝ h ＝ K dh K dt 飞升速度：＝ max 0 T
h t
K 0 F
t
（2-4）
能源与动力工程学院 2、特征参数 （1）飞升速度ε 飞升速度是指在单位阶跃扰动作用下，被控对象输出端被控量 的最大变化速度，根据定义可得：
dh K dt t 0 1 0 F Ta
（2）自平衡率ρ
因此飞升时间越大，被控量的变 化速度和系统的反应时间越慢。
t T
能源与动力工程学院
由上式可知，在t＝0时水位h的变化速度最快，代入可得：
K 0 h dh dt t 0 T T
在t＝0时水位h的变化速度等于图中响应曲线起始点切线 的斜率，因此当被控对象的输入端控制量产生阶跃变化后，输 出的被控量保持初始速度达到稳态值所需的时间即为时间常数 T。 当t＝3T时：
系统的输入量为输出量为主水槽水位h能源与动力工程学院1阶跃响应有自平衡双容水槽被控对象阶跃响应曲线能源与动力工程学院有自平衡双容水槽被控对象方框图2传递函数前置水槽主水槽25有自平衡双容水槽被控对象传递函数两个一阶惯性的串联双容对象放大系数前置水槽时间常数主水槽时间常数标准化
能源与动力工程学院
第二章 热工对象动态特性
1、阶跃响应与传递函数
Lesson-被控对象的特性
h
Qo
d h A Qi dt
7-2 被控对象特性的机理建模
则一阶非自衡对象传递函数为：
K Go ( s ) Ts
阶跃响应由右图所示。 对比一阶自衡对象传递函数： K Go ( s ) Ts 1
7-1 概述
建模方法： 机理建模 （白箱法） 属于解析法 根据被控过程的内在机理，运用物料或能 量平衡关系，用数学推理方法建模 实验建模 （黑箱法） 属于辨识法 根据被控过程的输入、输出实验数据，通 过过程辨识与参数估计方法建立被控过程 的数学模型
7-1 概述
混合建模 （灰箱法） 机理较清楚部分用机理演绎，不清楚部分 采用实验辨识，适于多级被控过程 先通过机理分析模型结构，然后利用实验 辨识确定其中参数
稳定时，Qi = Qo。 不稳定时，Qi↑，h ↑， 压力↑， Qo↑，直至Qi = Qo
i
h Qo
自衡与非自衡能力对象特性
1．有自衡能力对象的动态特性 有自衡能力的对象具有这样的性质： 当受到阶跃干扰作用使平衡状态遭到破坏 后，在不需要任何外力作用(即不进行控制) 下，依靠对象自身的能力，对象的输出 (被控变量)便可自发地恢复到新的平衡状态。
dh T h KQi dt
上式就是描述简单水槽对象特性的数学模型。 它是一个一阶常系数微分方程式。
7-2 被控对象特性的机理建模 2 一阶对象的特性分析 为了求单容水槽对象输出 h 在输入 Qi 作用下的变 化规律，可以对一阶微分方程式进行求解。 假定输入变量 Qi 为阶跃作用，即：
0 Qi Q
t 0 t 0
则微分方程式的通解为 h(t) = KQ + Ce-t /T 将初始条件h(0) = 0 代入上式，得到 h(t) = KQ (1- e-t /T)
第二章之1被控对象的特性
这种应用对象输入输出的实测数据来决定其模型的方法，通常称为系统辨识。其主要特 点是把被研究的对象视为一个黑箱子，不管其内部机理如何，完全从外部特性上来测试和描 述对象的动态特性。有时，为进一步分析对象特性，可对这些数据或曲线进行处理，使其转 化为描述对象特性的解析表达式。
混合建模——将机理建模与实验建模结合起来，称为混合建模。
h ( t ) / h2 ( t )
单容
响应曲线比较
· 纯滞后一阶对象 在工业过程中常有一些输送物料的中 间过程，如图所示，qi为操纵变量， 但需要经过导流槽才送入水箱。如果 把水箱入口的进料量记为qf，并设： 导流槽长度l，流体平均速度v，流体 流经导流槽所需的时间τ，所以当qi 发生改变以后，经过时间以后qf才 有变化：
d h2 dt
h2 K q i
( T1 A1 R1 T 2 A 2 R 2 K R 2 )
典型的传递函数
H 2 (s) Qi ( s )
K T1T 2 s (T1 T 2 ) s 1
2
K (T1 s 1)(T 2 s 1)
t T2
典型的阶跃响应函数 h 2 ( t ) K a [1
q f (t ) q i (t )
qi
qf
l/v
A, h
q0
对于qf与h来说，根据前面的推导，可知 ： d h (t )
T dt h (t ) K qi (t )
s
T
d h (t ) dt
h (t ) K q f (t )
传递函数为： T sH ( s ) H ( s ) K e
典型的微分方程 典型的传递函数 典型的阶跃响应函数
过程装备控制技术及应用习题及参考答案（精品pdf）
过程装备控制技术及应用习题及参考答案第一章控制系统的基本概念1.什么叫生产过程自动化？生产过程自动化主要包含了哪些内容？答：利用自动化装置来管理生产过程的方法称为生产过程自动化。
主要包含：①自动检测系统②信号联锁系统③自动操纵系统④自动控制系统。
2.自动控制系统主要由哪几个环节组成？自动控制系统常用的术语有哪些？答：一个自动控制系统主要有两大部分组成：一部分是起控制作用的全套自动控制装置，包括测量仪表，变送器，控制仪表以及执行器等；另一部分是自动控制装置控制下的生产设备，即被控对象。
自动控制系统常用的术语有：被控变量y——被控对象内要求保持设定数值的工艺参数，即需要控制的工艺参数，如锅炉汽包的水位，反应温度；给定值（或设定值）y s——对应于生产过程中被控变量的期望值；测量值y m——由检测原件得到的被控变量的实际值；操纵变量（或控制变量）m——受控于调节阀，用以克服干扰影响，具体实现控制作用的变量称为操纵变量，是调节阀的输出信号；干扰f——引起被控变量偏离给定值的，除操纵变量以外的各种因素；偏差信号（e）——被控变量的实际值与给定值之差，即e=y m-y s控制信号u——控制器将偏差按一定规律计算得到的量。
3.什么是自动控制系统的方框图？它与工艺流程图有什么不同？答：自动控制系统的方框图上是由传递方块、信号线（带有箭头的线段）、综合点、分支点构成的表示控制系统组成和作用的图形。
其中每一个分块代表系统中的一个组成部分，方块内填入表示其自身特性的数学表达式；方块间用带有箭头的线段表示相互间的关系及信号的流向。
采用方块图可直观地显示出系统中各组成部分以及它们之间的相互影响和信号的联系，以便对系统特性进行分析和研究。
而工艺流程图则是以形象的图形、符号、代号，表示出工艺过程选用的化工设备、管路、附件和仪表自控等的排列及连接，借以表达在一个化工生产中物料和能量的变化过程，即原料→成品全过程中物料和能量发生的变化及其流向。
第二章被控对象的数学模型
第二章被控对象的数学模型第二章被控对象的数学模型1(什么是被控对象特性?什么是被控对象的数学模型?研究被控对象特性有什么重要意义?答:被控对象持性是指被控对象输入与输出之间的关系。
即当被控对象的输入量发生变化时，对象的输出且是如何变化、变化的快慢程度以及最终变化的数值等。
对象的输入量有控制作用和扰动作用，输出量是被控变量。
因此，讨论对象特性就要分别讨论控制作用通过控制通道对被控变量的影响，和扰动作用通过扰动通道对被控变量的影响。
定量地表达对象输入输出关系的数学表达式、称为该对象的数学模型。
在生产过程中，存在着各种各样的被控对象。
这些对象的持性各不相同。
有的较易操作，工艺变量能够控制得比较平稳，有的却很难操作，工艺变量容易产生大幅度波动，只要稍不谨慎就会越出工艺允许的范围，轻则影响生产，重则造成事故。
只有充分了解和熟悉对象特性，才能使工艺生产在最佳状态下运行。
因此，在控制系统设计时、首先必须充分了解被控对象的特性，掌握它们的内在规律，才能选择合适的被控变量、操纵变量，合适的测量元件和控制器(选择合理的控制器参数，设计合乎工艺要求的控制系统。
特别在设计新型的控制系统时。
例如前馈控制、解偶控制、自适应控制、计算机最优控制等，更需要考虑被控对象特性。
2(简述建立对象的数学模型的两种主要方法。
答:一是机理分析法。
机理分析法是通过对对象内部运动机理的分析，根据对象中物理或化学变化的规律(比如三大守恒定律等)、在忽略一些次要因素或做出一些近似处理后推导出的对象特性方程。
通过这种方法得到的数学模型称之为机理模型，它们的表现形式往往是微分方程或代数方程。
二是实验测取法。
实验测取法是在所要研究的对象上，人为施加一定的输入作用，然后，用仪器测取并记录表征对象特性的物理量随时间变化的规律，即得到一系列实验数据或实验曲线。
然后对这些数据或曲线进行必要的数据处理，求取对象的特性参数，进而得到对象的数学模型。
3(描述简单对象特性的参数有哪些?各有何物理意义?答:描述对象特性的参数分别是放大系数K、时间常数T、滞后时间τ。
第2章被控对象的特性资料
i
(2-6)
式（2-5）或（2-6）就是描述简单水槽对象特性的数 学模型。它是一个一阶常系数微分方程式。
T为时间常数。 K 为放大系数。
2 一阶对象的特性分析 求单容水槽对象输出h在输入Qi作用下的变化规律，
可以对式（2-5）的一阶微分方程式进行求解。假定输 人变量Qi为阶跃作用，即
则式（2-5）的通解为
(2）放大系数K 由式（2-9）可以看出，在阶跃输入△Qi的作用下，
随着时间t→∞，液位将达到新的稳态值，其最终的变化 量为△h（∞）= K△Q，这就是说，一阶水槽的输出变化 量与输人变化量之比是一个常数。即
K h() Q
（2-12）
放大系数K 的物理意义可以理解为： 如果有一定的输入变化量△Q ，通过对象就被放
i
Q Q Q
0
s
0
将这些变量代入式（2-1）中，就可得到
Ad h Q Q
dt
ioΒιβλιοθήκη （2-2）在上式中，还不能清楚地看出h与Qi的关系。因为 式中有QO的存在，为此，必须将QO从式中消除。由工 艺设备的特性可知，QO与h 的关系是非线性的。考虑 到h和QO的变化量相对较小，可以近似认为QO与h 成正 比，与出水阀的阻力系数R 成反比，其具体关系式如
第二章 被控对象的特性
§2-1 概述
一、基本概念
过程控制系统的控制品质，是由组成系统的各环 节的特性所决定的，特别是被控对象的特性对整个控 制系统的运行的好坏有着重大影响。
常见的被控对象有各种类型的换热器、反应器、 精馏塔、加热炉、贮罐及流体输送设备等等。尽管这 些对象的几何形状和尺寸各异，内部所进行的物理、 化学过程也各不相同，但是从控制的观点来看，它们 在本质上却有许多共性，这便是研究对象特性的基础。
第2章 过程装备控制基础-2.1
• 其动态物料平衡关系有： 其动态物料平衡关系有：
dV dH Q1 − Q 2 = ＝A × dt dt
• 在静态时， dV/dt=0, Q1=Q2； 在静态时， ； • 发生变化时， 当Q1发生变化时，液位 将随之 发生变化时 液位H将随之 变化， 变化，水槽出口处的静压力随之 发生变化，流出量 亦发生变化 亦发生变化。 发生变化，流出量Q2亦发生变化。 假设其变化量很小， 假设其变化量很小，可近似认为 Q2与液位 成正比，而与出水阀 与液位H成正比 与液位 成正比， 的水阻R2成反比， 的水阻 成反比，即 成反比
1
dV 为贮存量的变化率 dt
Q1
Q2 2
H Q2 = R2
在讨论被控对象的特性时，被控对象的出水阀开度不变， 在讨论被控对象的特性时，被控对象的出水阀开度不变， 因此阻力R2为常数。所以有： 因此阻力 为常数。所以有： 为常数
dH A × R2 × + H = R2 × Q1 dt
令T = AR2＝R 2 C, K = R2 , 则
• 输入变量是控制系统的操纵变量和干扰信号， 输入变量是控制系统的操纵变量和干扰信号， 是控制系统的操纵变量和干扰信号 输出变量是控制系统的被控变量（控制要求）。 输出变量是控制系统的被控变量（控制要求）。 是控制系统的被控变量 • 被控对象输入变量与输出变量之间的联系称为通道。 被控对象输入变量与输出变量之间的联系称为通道。 通道
H
突然有一阶跃变化量△ ， 突然有一阶跃变化量△Q1，则相 应液位变化量
∆H = K × ∆Q1 1 − e
(
−( t −t 0 ) T
)
第二章被控对象的特性
研究过程特性的必要性： 研究过程特性的必要性： 必要性 为了更好地实施控制
医生给病人看病，其实也是控制思想的一种运用。看病 吃药的过程也就是克服干扰作用的过程，最终的目的是 使病人的身体好起来。那么，医生开处方怎么开呢？首 先他得了解病人的病情，然后才能对症下药。医生发解 病人病因的过程也就是了解对象特性的过程。所以说， 了解了对象的特性对于更好地控制好这个对象是有益的。
即对象受到输入作用后，被控变量是如何变化的、变化量为多少…… 即对象受到输入作用后，被控变量是如何变化的、变化量为多少……
输入量？？ 输入量？？
控制变量＋各种各样的干扰变量 控制变量＋
被控对象 干扰变量
干扰通道
由对象的输入变量至输出变量的信号联系称为通道 由对象的输入变量至输出变量的信号联系称为通道
本章研究内容： 本章研究内容：
2.1 对象特性的类型 2.2 对象特性的数学描述 2.3 对象特性的一般分析 2.4 对象特性的实验测定方法
2.1 对象特性的类型
对象特性——是指对象输入量与输出量之间的关系 数学模型) 对象特性——是指对象输入量与输出量之间的关系(数学模型) 是指对象输入量与输出量之间的关系(
qi q0
q0
左图：假设初始为平衡状态qi=qo，水箱水位保持不变。 水箱水位保持不变。 左图：假设初始为平衡状态q 当发生变化时( 当发生变化时(qi＞qo)，此时水箱的水位开始升高 根据流体力学原理，水箱出口流量与H是存在一定的对应关系的： 根据流体力学原理，水箱出口流量与H是存在一定的对应关系的： 因此， 因此，qi↑ ⇒ H ↑ ⇒qo↑，直至qi=qo可见该系统受到干扰以后，即使不加控制，最 直至q 可见该系统受到干扰以后，即使不加控制， 终自身是会回到新的平衡状态，这种特性称为“自衡特性” 终自身是会回到新的平衡状态，这种特性称为“自衡特性”。 右图：如果水箱出口由泵打出，其不同之处在于：qi当发生变化时，qo不发生变化。如 右图：如果水箱出口由泵打出，其不同之处在于： 当发生变化时， 不发生变化。 水位H将不断上升，直至溢出，可见该系统是无自衡能力。 果qi＞qo ，水位H将不断上升，直至溢出，可见该系统是无自衡能力。 绝大多数对象都有自衡能力，一般而言有自衡能力的系统比无自衡能力的系统容易控制。 绝大多数对象都有自衡能力，一般而言有自衡能力的系统比无自衡能力的系统容易控制。
2.1被控对象特性
y () y (0) K q() q(0)
滞后时间τ:是从阶跃扰动开始到对象输出值开始变化的时间。 时间常数T:响应曲线上找到输出稳态值的63.2%所对应的时 间与对象开始输出的时间差。
63.2%
T
对于二阶特性的对象其响应曲线稳态输出
与纵轴作垂直线1,响应曲线存在一个拐点,在拐点处作切线,分别与垂直线 1和横轴交于两点12。标记下这两点,选择垂直线1的交点1作横轴的垂线 交于横轴一点3,横轴上23两点的长度为时间常数T。
Kl——阀门的比例系数
令ΔQ1=q1，ΔQ2=q2
dhc q1 - q 2 dt S
H Q2 R2
流出量的变化量ΔQ2与水位的变化量ΔH成正比，与流出阀门2的阻力R2 成反比,即 即
hc q2 R2
假定水位变化不大，则R2可近似认为是一个常数
hc Kll 0 dhc q1 - q 2 R2 dt S S
单容水箱对象特性的实验测试
单容水箱的数学模型可用一阶惯性环节来近似描述，且用下述方法求取 对象的特征参数。
单容水箱液位开环控制结构图
设水箱的进水量为Q1，出水量为Q2，水箱的液面高度为h，出水阀V2固 定于某一开度值。根据物料动态平衡的关系，求得：
R 2C
在零初始条件下，对上式求拉氏变换，得：
G( s) H ( s) R2 K Q1( s) R 2CS 1 TS 1 2 -1
有纯滞后
d 2 yt dy (t ) Tc1Tc 2 ( T T ) y(t ) Kc q(t ) c1 c2 2 dt dt
二阶被控干扰控制通道的动态方程为：
d 2 yt dy(t ) T f 1T f 2 (T f 1 T f 2 ) y(t ) K f f (t ) 2 dt dt
现代控制原理第二章课后答案
第二章被控对象的数学模型第一章自动控制系统基本概念1.简述被控对象、被控变量、操纵变量、扰动(干扰)量、设定(给定)值和偏差的含义？答:自动控制系统中常用的几个术语其含义是：被控对象自动控制系统中，工艺参数需要控制的生产过程、设备或机器等。
被控变量被控对象内要求保持设定数值的工艺参数。
操纵变量受控制器操纵的，用以克服干扰的影响，使被控变量保持设定值的物料量或能量。
扰动量：除操纵变量外，作用于被控对象并引起被控变量变化的因素。
设定值：被控变量的预定值。
偏差：被控变量的设定值与实际值之差。
2.自动控制系统按其基本结构形式可分为几类?其中闭环控制系统中按设定值的不同形式又可分为几种?简述每种形式的基本含义。
答:自动控制系统按其基本结构形式可分为闭环自动控制系统和开环自动控制系统。
闭环自动控制是指控制器与被控对象之间既有倾向控制又有反向联系的自动控制。
如图1—1(a)即是一个闭环自动控制。
图中控制器接受检测元件及变送器送来的测量信号，并与设定值相比较得到偏差信号，再根据偏差的大小和方向，调整蒸汽阀门的开度，改变蒸汽流量，使热物科出口温度回到设定值上。
从图l—1(b)所示的控制系统方块图可以清楚看出，操纵变量(蒸汽流量)通过被控对象去影响被控变量，而被控变量又通过自动控制装置去影响操纵变量。
从信号传递关系上看，构成了一个闭合回路。
在闭环控制系统中，按照没定值的不同形式又可分为：(1)定值控制系统定值控制系统是指设定值恒定不变的控制系统。
定值控制系统的作用是克服扰动对被控变量的影响，使被控变量最终回到设定值或其附近。
以后无特殊说明控制系统均指定值控制系统而言。
(2)随动控制系统随动控制系统的设定值是不断变化的。
随动控制系统的作用是使被控变量能够尽快地、准确无误地跟踪设定值的变化而变化。
(a)(b)图1-1闭环自动控制基本结构(3)程序控制系统程序控制系统的设定值也是变化的，但它是一个已知的时间函数,即设定值按一定的时间程序变化。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
F2
无自衡的非振荡过程如下图中的液位过程
F1
h f(t)
h(t)
h(0)
t
(a)
F2
2.2 对象特性的数学描述
问题：处于平衡状态的对象加入干扰以后，不经控制系统能否自行达到新的平衡状态？
qi
qi
q0
q0
左图：假设初始为平衡状态qi=qo，水箱水位保持不变。 当发生变化时(qi＞qo)，此时水箱的水位开始升高 根据流体力学原理，水箱出口流量与H是存在一定的对应关系的： 因此，qi H qo，直至qi=qo可见该系统受到干扰以后，即使不加控制，最 终自身是会回到新的平衡状态，这种特性称为“自衡特性”。
本章研究内容：
2.1 对象特性的类型 2.2 对象特性的数学描述 2.3 对象特性的一般分析 2.4 对象特性的实验测定方法
2.1 对象特性的类型
对象特性——是指对象输入量与输出量之间的关系(数学模型)
即对象受到输入作用后，被控变量是如何变化的、变化量为多少……
输入量？？ 控制变量＋各种各样的干扰变量
由对象的输入变量至输出变量的信号联系称为通道
干扰变量
控制变量至被控变量的信号联系通道称控制通道 干扰至被控变量的信号联系通道称干扰通道
控制变量
被控对象
干扰通道 控制通道
被控变量
对象输出为控制通道输出与各干扰通道输出之和
数学模型的表示方法：
参量模型：通过数学方程式表示 常用的描述形式：微分方程(组)*、传递函数*、频率特性等
dh00 dt
d h Td t hK q i
（ ii）
(i)式是针对完全量的输入输出模型，(ii)式是针对变化量的输入输出模型，二者的结构形 式完全相同。由于在控制领域中，特性的分析往往是针对变化量而言的，为了书写方便在 以后的表达式中不写出变化量符号。
qi
Td d th hK q i （ ii）
响应曲线有四种：
h(t)
θ(t)
h(0) (a)
t
θ(0)
t
(b)
有自衡的非振荡过程
h(t)
c(t)
h(0)
t
(a)
c(0)
t
(b)
无自衡的非振荡过程
c(t)
c(t)
c(0)
t
有自衡的振荡过程
c(0)
t
具有反向特性的过程
有自衡的非振荡过程如下图中的液位过程
1
F1
h(t)
h
h(0)
t
2
(a)
f(t)
非参量模型：采用曲线、表格等形式表示。 特点：形象、清晰，缺乏数学方程的解析性质（必要时须进行数学处 理获得参量模型）。
建模的方法：机理建模、实验建模、混合建模
机理建模——根据物料、能量平衡、化学反应、传热传质等基本方程，从理论上来推导建立数学 模型。
由于工业对象往往都非常复杂，物理、化学过程的机理一般不能被完全了解，而且线性的 并不多，再加上分布元件参数（即参数是时间与位置的函数）较多，一般很难完全掌握系统内 部的精确关系式。另外，在机理建模过程中，往往还需要引入恰当的简化、假设、近似、非线 性的线性化处理等，而且机理建模也仅适用于部分相对简单的系统。
参量模型的微分方程的一般表达式：
y ( n ) ( t ) a n 1 y ( n 1 ) ( t ) a 1 y ( t ) a 0 y ( t ) b m x ( m ) ( t ) b 1 x ( t ) b 0 x ( t )
y(t)表示输出量，x(t)表示输入量，通常输出量的阶次不低与输入量的阶次(n≥m) 当n=m时，称对象是正则的；当n>m时，称对象是严格正则的；n<m的对象是不可 实现的。通常n=1，称该对象为一阶对象模型；n=2，称二阶对象模型。
qi Ah
q0
根据物料平衡方程： 单位时间内水槽体积的改变＝输入流量 — 输出流量
dV dt
qi
qo
V Ah
A dh dt
qi
qo
由于出口流量可以近似地表示为：q o
h R
A
dh dt
qi
h R
T d d h t h K q i (T A R 、 K R ) （ i）
记 h qi h q 0i0 hqi(h0、 qi0为 平 衡 状 态 的 值 ）由 于 有 h0Kqi0
通道：输入变量对输出变量的作用途径
控制通道：操纵变量q(t)对被控变量c(t)的作用途径
扰动通道：扰动变量f(t)对被控变量c(t)的作用途径
广义对象特性主要通过响应曲线来呈现
控制通道的响应曲线：当被控作用u(t)做阶跃变化（扰动f(t) 不变）时被控变量的时间特性c(t)
扰动通道的响应曲线：当扰动f(t)做阶跃变化（控制作用u(t) 不变）时被控变量的时间特性c(t)
混合建模——将机理建模与实验建模结合起来，称为混合建模。
混合建模是一种比较实用的方法，它先由机理分析的方法提出数学模型的结构形 式，把被研究的对象视为一个灰箱子，然后对其中某些未知的或不确定的参数利用实 验的方法给予确定。这种在已知模型结构的基础上，通过实测数据来确定数学表达式 中某些参数的方法，称为参数估计。
实验建模——在所要研究的对象上，人为的施加一个输入作用，然后用仪表记录表征对象特性的 物理量随时间变化的规律，得到一系列实验数据或曲线。这些数据或曲线就可以用 来表示对象特性。
这种应用对象输入输出的实测数据来决定其模型的方法，通常称为系统辨识。其主要特点 是把被研究的对象视为一个黑箱子，不管其内部机理如何，完全从外部特性上来测试和描述对 象的动态特性。有时，为进一步分析对象特性，可对这些数据或曲线进行处理，使其转化为描 述对象特性的解析表达式。
第二章被控对象的特性
研究过程特性的必要性：
为了更好地实施控制
医生给病人看病，其实也是控制思想的一种运用。看病 吃药的过程也就是克服干扰作用的过程，最终的目的是 使病人的身体好起来。那么，医生开处方怎么开呢？首 先他得了解病人的病情，然后才能对症下药。医生发解 病人病因的过程也就是了解对象特性的过程。所以说， 了解了对象的特性对于更好地控制好这个对象是有益的。
右图：如果水箱出口由泵打出，其不同之处在于：qi当发生变化时，qo不发生变化。如 果qi＞qo ，水位H将不断上升，直至溢出，可见该系统是无自衡能力。
绝大多数对象都有自衡能力，一般而言有自衡能力的的对象模型（输入输出模型）。 解： 该对象的输入量为qi 被控变量为液位h