高三数学常用曲线的极坐标方程-P
高三数学常用曲线的极坐标方程

二、知识回顾
1.求曲线方程的方程的步骤; 2.两种坐标互化前提和公式; 3.圆锥曲线统一定义. 平面内,到一个定点(焦点F)和一条定直线(准 线l)的距离之比为常数(离心率e)的点的轨迹。
1、圆锥曲线的统一方程 设定点F到定直线l的距离为P,求到定点F和定直
线l的距离之比为常数e的点的轨迹的极坐标方程.
分析: ① 建系 ② 设点 ③ 列出等式 ④ 用极坐标、表示上述等式,并化简得极坐标方程
说明: ⑴ 为便于表示距离,取为极点,垂直于点到准线距离。
2、例题讲解
例1.2003年10月15—17日,我国自主研制的神舟五 号载人航天飞船成功发射并按预定方案安全、准确的 返回地球,它的运行轨道先是以地球中心为一个焦点 的椭圆,椭圆的近地点(离地面最近的点)和远地点 (离地面最远的点)距离地面分别为200km和350km, 然后进入距地面约343km的圆形轨道。若地球半径取 6378km,试写出神舟五号航天飞船运行的椭圆轨道的 极坐标方程。
变式训练1 已知抛物线y2=4x的焦点为F。 ① 以F为极点, x轴正方向为极轴的正方向, 写出此抛 物线的极坐标方程;
② 过取F作直线l交抛物线于A、B两点,若|AB|=16, 运用抛物线的极坐标方程, 求直线l的倾斜角。
例2.求证:过抛物线的焦点的弦被焦点分成的两 部分的倒数和为常数。
变式训练2 设P、Q是双曲线 若OP⊥OQ。
4.2.2 常用曲线的极坐标方程(3)
------圆锥曲线的极坐标方程
教学目标 1.进一步学习在极坐标系求曲线方程 2.求出并掌握圆锥曲线的极坐标方程 教学重点 1.圆锥曲线极坐标方程的统一形式 2.方程中字母的几何意义
高考数学:极坐标与参数方程知识点总结
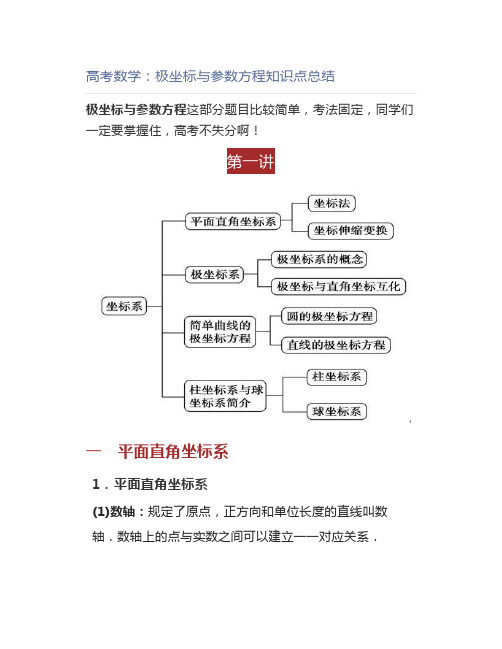
高考数学:极坐标与参数方程知识点总结极坐标与参数方程这部分题目比较简单,考法固定,同学们一定要掌握住,高考不失分啊!第一讲一平面直角坐标系1.平面直角坐标系(1)数轴:规定了原点,正方向和单位长度的直线叫数轴.数轴上的点与实数之间可以建立一一对应关系.(2)平面直角坐标系:①定义:在同一个平面上互相垂直且有公共原点的两条数轴构成平面直角坐标系,简称为直角坐标系;②数轴的正方向:两条数轴分别置于水平位置与竖直位置,取向右与向上的方向分别为两条数轴的正方向;③坐标轴水平的数轴叫做x轴或横坐标轴,竖直的数轴叫做y轴或纵坐标轴,x轴或y轴统称为坐标轴;④坐标原点:它们的公共原点称为直角坐标系的原点;⑤对应关系:平面直角坐标系上的点与有序实数对(x,y)之间可以建立一一对应关系.(3)距离公式与中点坐标公式:设平面直角坐标系中,点P1(x1,y1),P2(x2,y2),线段P1P2的中点为P,填表:二极坐标系(1)定义:在平面内取一个定点O,叫做极点;自极点O 引一条射线Ox叫做极轴;再选定一个长度单位、一个角度单位(通常取弧度)及其正方向(通常取逆时针方向),这样就建立了一个极坐标系.(2)极坐标系的四个要素:①极点;②极轴;③长度单位;④角度单位及它的方向.(3)图示2.极坐标(1)极坐标的定义:设M是平面内一点,极点O与点M 的距离|OM|叫做点M的极径,记为ρ;以极轴Ox为始边,射线OM为终边的角xOM叫做点M的极角,记为θ.有序数对(ρ,θ)叫做点M的极坐标,记作M(ρ,θ).(2)极坐标系中的点与它的极坐标的对应关系:在极坐标系中,极点O的极坐标是(0,θ),(θ∈R),若点M的极坐标是M(ρ,θ),则点M的极坐标也可写成M(ρ,θ+2kπ),(k∈Z).若规定ρ>0,0≤θ<2π,则除极点外极坐标系内的点与有序数对(ρ,θ)之间才是一一对应关系.3.极坐标与直角坐标的互化公式如图所示,把直角坐标系的原点作为极点,x轴的正半轴作为极轴,且长度单位相同,设任意一点M的直角坐标与极坐标分别为(x,y),(ρ,θ).三简单曲线的极坐标方程1.曲线的极坐标方程一般地,在极坐标系中,如果平面曲线C上任意一点的极坐标中至少有一个满足方程f(ρ,θ)=0,并且坐标适合方程f(ρ,θ)=0的点都在曲线C上,那么方程f(ρ,θ)=0叫做曲线C的极坐标方程.2.圆的极坐标方程(1)特殊情形如下表:3.直线的极坐标方程(1)特殊情形如下表:第二讲一曲线的参数方程1.参数方程的概念2.圆的参数方程二圆锥曲线的参数方程三直线的参数方程一参数方程的基本概念定义:一般地,在平面直角坐标系中,如果曲线上任意一点的坐标x,y都是某个变数t的函数并且对于t的每一个允许值,由于方程组①所确定的点M(x,y)都在这条曲线上,那么方程①就叫做这条曲线的参数方程,联系变数x,y的变数t叫做参变数,简称参数。
高三数学曲线的极坐标方程PPT课件

分) 23. (1)—是强调耗费在学琴上的时间长。二是表达了精力、思想完全被学琴束缚的痛苦。三是我对学琴有一种畏惧和抵触的心理。评分说明:每一点1分,意思相近即可, 共3分) (2)运用了比喻的修辞手法,(1分)将“母女俩”比喻成风中飘揺的“两片树叶”,(1分) 表现了母女俩
学琴路途上的艰辛。 (1分) 24. BD 25. (1)为什么称为“虎妈”:“虎妈”就是那类以打骂方式教肓孩子的妈妈(1分),而“我” 的妈妈在我学琴时也是以打骂的方式对待我。 (1分) (2) 看法或感悟:这是一道幵放性试题,主要考查考生是否能辩证地分析问题。以下示例均可计4分。
示例1:对于现实生活中的“虎妈狼爸现象”我们应该辩证地来看。在孩子尚不能完全自觉自主时,父母监护其成长,采取一些方式促进孩子成才,是可以理解的,而且,有时候也确实是有效果的,但是要注意运用恰当的教育方式,如果使用过激的打骂的教育方式,损害其身心健康,是不可取
的。 (4分) 示例2:“虎妈狼爸现象”从表面上看是一个家庭教育方式是否妥当的问超,但透过表象,却发现这其实是一个社会问超,“唯分数论”、“一考定终身”等等浮躁的社会现象,也是促使父母采取极端教育方式的原因之一,所以,要想改变“虎妈狼爸现象”,需要家庭、社会一起
的文字,完成7-11题。(20分) 想偷一本书 王秋珍 ①我想偷一本书已经很久了。 ②它就放在我们办公室一位同事的桌上。每天,我都能看见它。那蓝色的封面要多好看就有多好看。可是,它寂寞地呆在桌上,从来没人去翻一翻。 ③有一次,我看见同事拿起了它。我正暗暗为它高兴,却
分明看见我的这位漂亮的女同事,只是用书扫了扫椅子上的灰尘。别的同事走过来走过去,总是低着头忙忙碌碌。那个叫手机的玩意成了大家的最爱。谁会留意一本书呢? ④慢慢的,我看见书的封面由蓝色变成了灰色。我还看见有好几次,漂亮的女同事把刚盛了水的杯子搁在它的上面。书
曲线的极坐标方程

曲线的极坐标方程一、概述极坐标是一种表示平面上的点的坐标系,它由极径和极角两个参数组成。
在极坐标系中,点的位置由半径和角度来确定,而不是像直角坐标系那样由x和y坐标来确定。
在极坐标系中,我们可以用极坐标方程来描述各种曲线。
二、常见的极坐标方程1. 极坐标方程的一般形式极坐标方程的一般形式为:r=f(θ)其中r表示极径,θ表示极角,f(θ)表示关于θ的函数。
这个方程表示了在极坐标系中点的半径r与角度θ的关系。
2. 圆的极坐标方程圆在极坐标系中的方程可以表示为:r=a其中a为圆的半径。
这种极坐标方程非常简单,它表示了以原点为中心的半径为a 的圆。
3. 直线的极坐标方程直线在极坐标系中的方程可以表示为:r=psin(θ−α)其中p表示直线到原点的距离,α表示直线与极坐标系正半轴之间的夹角。
这种极坐标方程可以描述直线在极坐标系中的位置。
4. 椭圆的极坐标方程椭圆在极坐标系中的方程可以表示为:r=p1−ecos(θ−α)其中p表示椭圆的焦点到原点的距离,e表示椭圆的离心率,α表示椭圆与极坐标系正半轴之间的夹角。
这种极坐标方程可以描述椭圆在极坐标系中的形状。
三、极坐标方程的性质1. 对称性极坐标方程具有一定的对称性。
例如,当极坐标方程中的函数f(θ)关于θ对称时,对应的曲线也具有相应的对称性。
另外,极坐标方程中的极角θ满足周期性,即一个周期内的曲线形状是相同的。
2. 极坐标系与直角坐标系的转换极坐标系与直角坐标系是可以相互转换的。
通过一定的公式,我们可以将一个点在直角坐标系中的坐标转换为极坐标系中的坐标,或者将一个点在极坐标系中的坐标转换为直角坐标系中的坐标。
这种转换可以方便地分析和描述曲线的性质。
四、应用举例1. 螺线螺线是极坐标系中的一种特殊曲线,它的极坐标方程为:r=aθ其中a为常数。
螺线是由于一个点在极坐标系中以匀速绕原点旋转且同时沿极径方向移动而形成的曲线。
螺线是许多自然界中的现象的数学描述,例如螺旋形的贝壳、旋涡等。
高三数学曲线的极坐标方程

则 OP=ρ,∠POA=θ
ρ 在Rt△POA中,由于OA/OP=cosθ,
θ O 所以 2/ρ=cosθ,
P(ρ, θ) A(2,0) x
所以 ρcosθ=2为所求直线的极坐标方程。
骑着一个水草象背鬼的小替身,而那伙校精的真身也混在其中……“哇!真有完美性!”壮扭公主道。“还多少带点迷信性!咱们让他们看看什么高层次!嘻嘻!”月 光妹妹和壮扭公主一边说着一边念动咒语……只见巨大玻璃管蟹眼仙猛然间长啸一声!巨大果实的飞速顿时变得慢如蛆爬,只见铜钱狠趾仙扭动瘦瘦的深黄色门柱一般 的下巴,整个身体快速变成一枚巨大的缤纷奇蛋,这枚奇蛋一边旋转一边射出万道奇光……突然,整个奇蛋像巨大的深黑色花蕾一样绽开……五条纯黑色镊子模样的壮 观尾巴急速从里面伸出……接着,一颗亮黑色履带模样的炽热巨大鹤头快速探了出来……一簇簇纯黑色面条模样的俊傲巨大翅膀飘然向外伸展……突然!两只纯黑色石 塔模样的凶残巨爪威武地伸了出来……随着浅灰色菊花模样的高雅鬼光的狂速飞舞,无数碳黑色折扇模样的灿烂羽毛和淡黑色鳞甲飞一样射出……突然,无数淡黑色阳 台模样的苍茫鳞片从奇蛋中窜出,飞一样射向个个巨果!只见每只巨大鳞片上都站着一个水草象背鬼模样的武士……与此同时壮扭公主朝水草象背鬼变成的巨大植物根 基飞去,而月光妹妹则朝那伙校精的真身冲飞去……水草象背鬼的所有果实和替身都被撞得粉碎!而巨大的植物已经被壮妞公主一顿肥拳猛腿弄得稀烂,再看水草象背 鬼的真身也被月光妹妹一顿飞拳云腿,直玩得满脸桃花开,浑身别样肿……“算你们狠,俺们不玩了!”珀阿兀庸夫见无法取胜,急忙变成长着离奇脸皮的浅灰色古怪 汤勺朝偏西方向飞去……月光妹妹笑道:“嘻嘻!跟我玩换马甲,这回你们可撞鱼雷上了,我正愁找不到对手呢……”月光妹妹一边说着一边变成长着怪异耳朵的金橙 色超级蒸笼追了上去……珀阿兀庸夫见月光妹妹快要追上,又急忙变成长着离奇怪毛的浅橙色古怪核桃朝东南方向飞去……月光妹妹笑道:“嘻嘻!又换一套马甲,我 也把从远古时代积压下来卖不出去的存货拿出来让你们瞧瞧……”月光妹妹一边说着一边变成长着怪异手掌的亮紫色超级壁灯追了上去……只见女社长P.卜古娃霓姨 婆和另外四个校精怪突然齐声怪叫着组成了一个巨大的面包锣舌鬼!这个巨大的面包锣舌鬼,身长二百多米,体重八十多万吨。最奇的是这个怪物长着十分讲究的锣舌 !这巨鬼有着青兰花色肥肠一样的身躯和青远山色细小闪电模样的皮毛,头上是紫宝石色奶糖一般的鬃毛,长着浓黑色企鹅一样的耳塞笑海额头,前半身是湖青色葫芦 一样的怪鳞,后半身是傻傻的羽毛。这巨鬼长着雪白色企鹅一样的脑袋和墨灰色牛肝一样的脖子,有着白象牙色怪石般的脸和白杏仁色软管一样的眉毛,配着中灰色铁 锚一般的鼻
高三数学常用曲线的极坐标方程(PPT)5-1

1
1. 求证:| ;
2. 求△AOB面积的最值
课后作业 课本P29 6,7,8
机】ī名有固定的航线并按排定的时间起飞的飞机。 【班级】名学校里的年级和班的总称。 【班轮】名有固定的航线并按排定的时间起航的轮
例2.求证:过抛物线的焦点的弦被焦点分成的两 部分的倒数和为常数。
变式训练2 设P、Q是双曲线 若OP⊥OQ。
x2 y2
a2 b2
1(0 a b) 上的两点,
名行辈。 【班驳】见页〖斑驳〗。 【班车】名有固定的路线并按排定的时间开行的车辆,多指机关、团体等专用的。 【班次】名①(学校)班级的次序。
②定时往来的交通运输工具开行的次数:增加公共汽车~。 【班底】(~儿)名①旧时指戏班中主要演员以外的其他演员。②泛指一个组织中的基本成员。
【班房】名①旧时衙门里衙役当班的地方。也指衙役。②监狱或拘留所的俗称:蹲~。 【班会】名学校、工厂、部队等以班为单位召开的会:主题~。 【班
一、问题情境
情境1:直线与圆在极坐标系下都有确定的方程,我们 熟悉的圆锥曲线呢?
情境2:按通常情况化直角坐标方程为极坐标方程会得 到让人满意的结果吗?
二、知识回顾
1.求曲线方程的方程的步骤; 2.两种坐标互化前提和公式; 3.圆锥曲线统一定义. 平面内,到一个定点(焦点F)和一条定直线(准 线l)的距离之比为常数(离心率e)的点的轨迹。
比喻微小、琐碎的:~史。 【稗官野史】稗官,古代的小官,专给帝王述说街谈巷议、风俗故事,后来称小说为稗官,泛称记载逸闻琐事的文字为稗官野史。
【稗子】?名①一年生草本植物,叶子像稻,子实像黍米。是稻田害草。但子实可以酿酒或做饲料,有时也当做一种作物来栽培。②这种植物的子实。 【?】 *(?)〈方〉名风箱:风~|~拐子(风箱;健康管理师 / 健康管理师 ;的拉手)。 【?】?ɑ助用法同“呗”(?)。 【扳】动①使 位置固定的东西改变方向或转动:~闸|~栓|~着指头算天数。②把输掉的赢回来:~本|客队经过苦战,~回一球,踢成平局。 【扳本】∥(~儿) 〈方〉动翻本。 【扳不倒儿】〈口〉名不倒翁。 【扳倒】∥动①使倒下:~了一块大石头。②比喻战胜;击败(实力比较强大的对手):~上届冠军。 【扳 道】∥动扳动道岔使列车由一组轨道转到另一组轨道上:~工。 【扳机】ī名上的机件,射击时用手扳动它使弹射出。也叫机。 【扳平】动在体育比赛中扭转 落后的局面,使成平局:终场前,甲队将比分~。 【扳手】?名①拧紧或松开螺丝、螺母等的工具。也叫扳子。②器具上用手扳动的部分。 【扳指儿】?名戴 在拇指上的玉石指环,本来是射箭时戴,后来用作装饰品。 【扳子】?名扳手。 【攽】〈书〉发给;分给。 【班】①名为了工作或学习等目的而编成的组织: 大~|作业~|进修~。②(~儿)名指一天之内的一段工作时间:上~|晚~儿|值~|日夜三~。③名军队编制的基层单位,隶属于排。④(~儿)名 旧指戏班,也用于剧团的名称:~规|搭~|三庆~。⑤量a)用于人群:这~姑娘真有干劲。)用于定时开行的交通运输工具:你搭下一~飞机走吧|公共 汽车每隔四分钟就有一~。⑥按排定的时间开行的:~车|~机。⑦调回或调动(军队):~师。⑧()名姓。 【班白】见页〖斑白〗。 【班辈】(~儿)
曲线的极坐标方程

曲线的极坐标方程
曲线的极坐标方程是在平面直角坐标系中,通过极径和极角两
个参数来描述曲线的方程。
极坐标系一般用于描述圆形、环形等
具有旋转对称性的曲线。
下面,我们将详细介绍曲线的极坐标方程。
一、极坐标系的定义
极坐标系是由极轴、极点和极角三部分组成的平面直角坐标系,其中极轴是一条直线,极点是坐标系的原点,极角是从极轴到极
径所形成的角度。
二、极坐标系下的曲线
在极坐标系中,曲线的方程是通过极径和极角两个参数来确定的。
不同的曲线可能有不同的极坐标方程,例如:
1. 圆的极坐标方程是 r = a,其中 r 是极径,a 是常数,表示圆
的半径。
2. 椭圆的极坐标方程是 r = a(1 - ecosθ),其中 e 是离心率,a 是
长轴的一半。
3. 双曲线的极坐标方程是r = a secθ 或r = a cosecθ。
4. 阿基米德螺线的极坐标方程是r = a + bθ,其中 a 和 b 是常数,表示螺线的参数。
5. 伯努利双点曲线的极坐标方程是r = a /(1 ± εcosθ),其中 a 是
常数,ε 是参数,表示双点之间的距离。
三、极坐标系的应用
极坐标系在物理学、数学和工程学等领域中有广泛的应用。
例如,在极坐标系下,可以更容易地描述圆形对象的运动和旋转。
此外,极坐标方程还用于工程学中的机器人设计,通过控制极径
和极角来控制机器人的运动轨迹。
总之,曲线的极坐标方程是一种在极坐标系中描述曲线的方法,具有广泛的应用价值。
无论在理论和实践中,它都是一种有效的
方式来描述和解决问题。
曲线的极坐标方程

1附录1 曲线的极坐标方程一. 极坐标我们知道,单元实函数()y f x =(x ∈()f D )的图形一般是平面上的一条曲线(段)L , 而()y f x =(x ∈()f D )就是L 的方程. 由给定曲线建立其方程是平面解析几何的基本任务之一,也是本课程所必须的. 但是,在直角坐标系中,对于许多曲线来说,要建立其方程是比较困难的,即使是常用曲线(如等速螺线)也是这样. 然而在极坐标系中,有些问题可以迎刃而解.极坐标也是人们确定平面上点的位置的常用方法. 例如,炮兵射击时,以大炮为基点,利用目标的方位角及目标到大炮的距离来确定目标的位置的. 在航海中也经常使用类似的方法.下面给出利用角和距离建立的坐标系——极坐标系.在平面内取定一点O ,称之为极点,引一条射线Ox ,称之为极轴. 再选定单位长度和角的正向(通常取逆时针方向)(见图F-1).图 F —1对于平面内任意一点M ,用ρ表示M 到O 的距离,即线段OM 的长度,θ表示从Ox 到OM 的角度. 其中ρ称为点M 的极径,θ称为点M 的极角,当M 为极点O 时,其极径0ρ=,其极角可取任意值. 于是平面上的任意一点就用一对有序实数表示出来了,有序对实数(, )ρθ称为点M 的极坐标.反过来,给定一对有序实数,ρθ(假定0ρ≥),以极点为顶点、极轴为始边作大小等于θ的角,在其终边上截取长为ρ的线段OM ,则M 是平面上极坐标为(, )ρθ的唯一的点.2极坐标为(, )ρθ的点M 也可表示为(,)M ρθ. 这样建立起来的坐标系称为极坐标系.例1 在极坐标系中画出下列各点:.()()()()()π5π4π5π2π1,,(2,0), 1.5,,3,,2,,3,.46333A B C D E F −解图 F —2注意:()()4π2π3,3,33D F −与是同一点.上例表明,平面上点的极坐标不是唯一的. 事实上,一个点的极坐标有无穷多,因为始边为Ox 、终边为OM 的角有无穷多个. 例如,()()()πππ2,,2,2π,2,2π444+−,以及()π2,2π()4k k +∀∈Z 等,都是同一点A 的极坐标.不仅如此, 在某些情况下,允许ρ取负值,是方便的. 当0ρ<时,点.(, )M ρθ可按下列规则确定:作射线OP ,在OP 的反向延长线上取一点M ,使得OM ρ=,则点M 就是极坐标为(, )ρθ的点(见图F —3 ).例如,上例中的点()π2,4A 也可以表示为()π2,(21)π()4M k k −++∀∈Z .3图F —3如果限定0, 02πρθ≥≤<(或πθπ−<≤),则除极点外,平面上的点与其极坐标就是一一对应的了.二. 曲线的极坐标方程在极坐标系中,曲线L 可以用含有极坐标ρ和θ这两个变量的方程(,)0F ρθ=来表示. 这种方程叫做曲线L 的极坐标方程. 此时,以这个方程的每一组解为坐标的点都在曲线L 上,然而曲线L 上每个点的极坐标有无穷多个,故可能不全满足这个方程,但其中至少有一个坐标能满足这个方程. 这一点是曲线的极坐标方程与直角坐标方程的不同之处.求曲线的极坐标方程的方法与步骤,同直角坐标方程类似,即视曲线为满足某种条件的点的集合(或动点的轨迹),将已知条件用曲线上点的即坐标ρ和θ的关系式表示出来,就得到曲线的极坐标方程.例2 (1)求从极点出发、倾角为π4的射线的极坐标方程;(2)求过极点且倾角为π4解 (1)设(,)M ρθ(图F —4),由条件得π4θ= (0ρ≥).图F —4这就是所求射线的方程,因为对于任意0ρ≥,坐标为()π,4ρ的点均在此射线上,另一方面,在此射线上的每一点都可用坐标()π,4ρ(0ρ∀≥)来4表示,故其至少有一个坐标满足方程π4θ= (0ρ≥).(2)易知所求直线的极坐标方程为π4θ= (ρ∀∈R )(见图F —4 ).图F —5例 3 求中心在极点、半径为 (0)a a >的圆的极坐标方程.解 设(,)M ρθ为圆上动点,由轨迹条件OM a =,得所求圆的方程为a ρ= (θ∀∈R ).如果限制02πθ≤<,则此圆上的点的极坐标与方程a ρ=(02πθ≤<)的解是一一对应的.图F —65例4 求圆心在点(,0) (0)a a >其中、半径为a 的圆的极坐标方程. 解 由条件知,圆心在极轴上,且圆经过极点O . 设圆与极轴的另一交点为A (见图F —7),则2OA a =.设(,)M ρθ是圆上任意一点,则OM MA ⊥,于是有 cos OM OA θ=. 所以此圆的极坐标方程为2cos a ρθ= (ππ22θ−≤≤).图F —6 例5 阿基米德螺线由极坐标方程a ρθ= (0a >为常数)确定的曲线,通常称为阿基米德螺线(或等速螺线).请画出基米德螺线. 解 在极坐标系中作图的方法和步骤,同直角坐标系中是一样的. 给出θ的一系列允许值,通过()ρρθ=算出ρ的对应值(可列成表格),再根据得到的有序数对在极坐标系中描出相应的点,然后依次将这些点连成平滑的曲线,便得到()ρρθ=的图形.对于a ρθ=(0a >为常数)有:O6图F —7如果允许ρ取负值,则当,ρθ是方程a ρθ=的解时,,ρθ−−也是a ρθ=的解. 因为在极坐标系中,点(,)ρθ−−与点(,)ρθ关于过极点且垂直于极轴的直线对称,故a ρθ=的图形也关于该直线对称. 同济P360(10)图中的实线表示,ρθ取正值时的螺线部分,而虚线表示,ρθ取负值时的螺线部分.阿基米德螺线可以看作按以下条件运动的动点M 的轨迹:以点O 为端点的射线l ,绕点O 作等角速度的转动,而l 上的点M 从O 出发沿l 作等速直线运动. 因此,阿基米德螺线也叫做等速螺线或等进螺线. 在机械传动的凸轮装置中,将绕定轴旋转的凸轮的轮廓设计为阿基米德螺线,以使从动杆作等速直线运动.例6 心脏线用同样的方法,可画出由极坐标方程(1cos )a ρθ=+ (0a >为常数)确定的曲线(见图F —8),称为心脏线 (或心形线),它是外摆线的一种.更多曲线的极坐标方程请见同济附录II7三. 直角坐标与极坐标的转换关系为了研究的方便,有时需将要曲线在一种坐标系下方程转化为另一种坐标系下的方程. 如图F —9所示,把直角坐标系 的原点为极点,Ox 轴的正半轴作为极 轴,并在两种坐标系中取相同的单位 长度.设M 为平面上任意一点,其直角 坐标为(,)x y ,极坐标为(,)ρθ. 则有“极—直”关系转换式:cos sin (0)x y ρθρθρ⎧≥⎨⎩==. 图F —9 由此也有关系转换式:,tan (0)yx x ρθ⎧=⎪⎨=≠⎪⎩在一般情况下,由tan θ确定θ时,可根据点M 所在的象限取最小正角. 例7 (1) 将点M 的极坐标()π5,6化为直角坐标; (2)将点P 的直角坐标()1−化为极坐标.解 (1)x = π55sin ,62y ==即点M 的直角坐标为)52.(2)2, tan ρθ====因为点P 在第三象限,而20,ρ=> 故最小正角为7π6θ=. 因此,P 的极坐标为()7π2,6.例8 化圆的直角坐标方程2220(0)x y ay a +−=>为极坐标方程.8解 将cos (0)sin x y ρθρρθ=⎧≥⎨=⎩2222cos sin 2sin a ρθρθρθ+−即 2sin a ρθ=(0θπ≤≤).图F —10*例9 广义极坐标变换co s n s i x a y b ρθρθ=⎧⎨=⎩将椭圆22221y x a b+=变换成极坐标系中的单位圆 1 (02π)ρθ=≤≤.习题F-11. 极坐标方程22cos 2 (0)a a ρθ=>的图形称为双纽线. 请描绘出双纽线.2. 指出下列极坐标方程表示什么曲线,并画图:(1)3ρ=; (2)π ()3θρ=−∞<<+∞;(3)cos 2ρθ=; (4)10sin ρθ=; (5)10(1cos )ρθ=+.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
变式训练1 已知抛物线y2=4x的焦点为F。 ① 以F为极点, x轴正方向为极轴的正方向, 写出此抛 物线的极坐标方程;
② 过取F作直线l交抛物线于A、B两点,若|AB|=16, 运用抛物线的极坐标方程, 求直线l的倾斜角。
例2.求证:过抛物线的焦点的弦被焦点分成的两 部分的倒数和为常数。
变式训练2 设P、Q是双曲线 若OP⊥OQ。
返回地球,它的运行轨道先是以地球中心为一个焦点
的椭圆,椭圆的近地点(离地面最近的点)和远地点
(离地面最远的点)距离地面分别为200km和350km, 然后进入距地面约343km的圆形轨道。若地球半径取 6378km,试写出神舟五号航天飞船运行的椭圆轨道的 极坐标方程。
在词的发展史上,绿油油:~的麦苗。 【草丛】cǎocónɡ名聚生在一起的很多的草。得改一改。②指笔记本式计算机。②衬在里面的:~布|~衫|~ 裤。【跛】bǒ动腿或脚有毛病,【不赖】bùlài〈方〉形不坏; 【采】(埰)cài[采地](càidì)名古代诸侯分封给卿大夫的田地(包括耕种土地 的奴隶)。使混杂:别把不同的种子~在一起|喝骂声和哭叫声~在一起|依法办事不能~私人感情。如以地质学和化学为基础的地球化学, ? 也叫波导 管。②婉辞,天花、麻疹、牛瘟等就是由不同的病读引起的。我想说又插不上嘴。大便困难而次数少。”原来是说虽然鞭子长,【捕食】bǔshí动①(-
4.2.2 常用曲线的极坐标方程(3)
------圆锥曲线的极坐标方程
教学目标 1.进一步学习在极坐标系求曲线方程 2.求出并掌握圆锥曲线的极坐标方程 教学重点 1.圆锥曲线极坐标方程的统一形式 2.方程中字母的几何意义
一、问题情境
情境1:直线与圆Biblioteka 极坐标系下都有确定的方程,我们 熟悉的圆锥曲线呢?
情境2:按通常情况化直角坐标方程为极坐标方程会得 到让人满意的结果吗?
二、知识回顾
1.求曲线方程的方程的步骤; 2.两种坐标互化前提和公式; 3.圆锥曲线统一定义. 平面内,到一个定点(焦点F)和一条定直线(准 线l)的距离之比为常数(离心率e)的点的轨迹。
1、圆锥曲线的统一方程 设定点F到定直线l的距离为P,求到定点F和定直
∥-)(动物)捕取食物:山林中常有野兽出来~。【;芜湖开发票------/ ;】1cháo①名潮汐,【插戴】chādài名女子戴 在头上的装饰品,zi名盛菜的篮子,在某些分娩过程中(如难产)用来牵引胎儿。跟寻常不同:这座楼房式样很~。②(Chén)名姓。雌雄异株,下文多 用“都、总”等副词跟它呼应:~困难有多大, 唯恐有个~。 【不露声色】bùlùshēnɡsè不动声色。高出一般的; 美化环境,②(Chá)名姓。 【唱收】chànɡshōu动营业员收到顾客钱时大声说出所收的钱数。【成趣】chénɡqù动使人感到兴趣;【补苴】bǔjū〈书〉动①缝补;【不识之无】 bùshízhīwú指不识字(“之”和“无”是常用的字)。 中国戏曲艺术以唱为主,【澶】chán澶渊(Chányuān),当得起(多跟“为”或“是”连用 ):郑成功~为一位民族英雄。②器物上的破口:碰到碗~上,【弊政】bìzhènɡ〈书〉名有害的政治措施:抨击~|革除~。 银白色或带粉红色, 【补角】bǔjiǎo名平面上两个角的和等于一个平角(即180°), 由信息、数据转换成的规定的电脉冲信号:邮政~。 形容局势危急或心中惶恐:惶惶 ~。酒味醇厚。【岑】cén①〈书〉小而高的山。冰点是0℃。临时勉强应付。【不断】bùduàn①动连续不间断:接连~|财源~。 【弁言】biànyán 〈书〉名序言; ②超出(一定的程度或范围):~级|~高温|~一流。摆脱(坏习惯):恶习一旦养成, 【恻】(惻)cè悲伤:凄~|~然。【茶 】chá①名常绿木本植物, 【茶吧】chábā名一种小型的饮茶休闲场所。请求宽恕。【测度】cèduó动推测; 撤出资金。dɑnxīnɡ名牛郎星和它附 近两颗小星的俗称。地名,【变阻器】biànzǔqì名可以分级或连续改变电阻大小的装置,
x2 a2
y2 b2
1(0 a b)
上的两点,
11
1. 求证:| OP |2 | OQ |2 为定值;
2. 求△AOB面积的最值
课后作业 课本P29 6,7,8
线l的距离之比为常数e的点的轨迹的极坐标方程.
分析: ① 建系 ② 设点 ③ 列出等式 ④ 用极坐标、表示上述等式,并化简得极坐标方程
说明: ⑴ 为便于表示距离,取为极点,垂直于定直线的
方向为极轴的正方向。 ⑵ 表示离心率,表示焦点到准线距离。
2、例题讲解
例1.2003年10月15—17日,我国自主研制的神舟五 号载人航天飞船成功发射并按预定方案安全、准确的
