转子动力学大作业
Ansys转子动力学
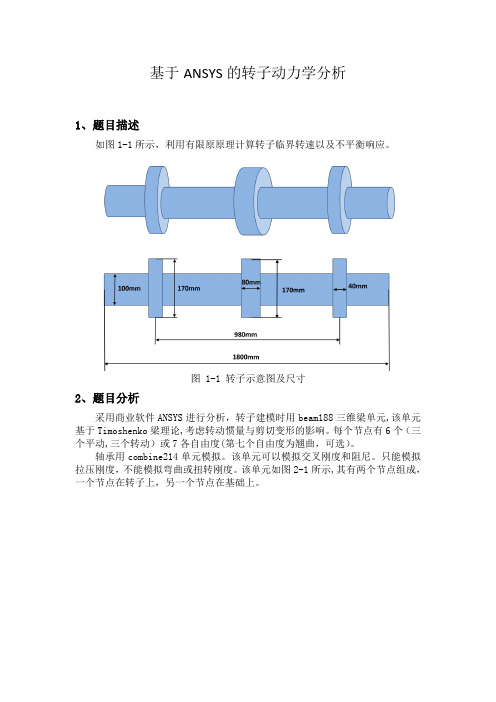
基于ANSYS的转子动力学分析1、题目描述如图1-1所示，利用有限原原理计算转子临界转速以及不平衡响应。
图 1-1 转子示意图及尺寸2、题目分析采用商业软件ANSYS进行分析，转子建模时用beam188三维梁单元,该单元基于Timoshenko梁理论,考虑转动惯量与剪切变形的影响。
每个节点有6个（三个平动,三个转动）或7各自由度(第七个自由度为翘曲，可选）。
轴承用combine214单元模拟。
该单元可以模拟交叉刚度和阻尼。
只能模拟拉压刚度，不能模拟弯曲或扭转刚度。
该单元如图2-1所示,其有两个节点组成，一个节点在转子上，另一个节点在基础上。
图 2-1 combine214单元对于质量圆盘，可以用mass21单元模拟，该单元有6个自由度，可以模拟X ，Y ，Z 三个方向的平动质量以及转动惯性。
3、计算与结果分析 3。
1 转子有限元模型建模时，采用钢的参数，密度取37800/kg m ,弹性模量取112.1110pa ，泊松比取0.3。
轴承刚度与阻尼如表1所示,不考虑交叉刚度与阻尼，且为各项同性。
Kxx Kyy Cxx Cyy 4e7N/m 4e7N/m 4e5N 。
s/m 4e5N 。
s/m将转子划分为93个节点共92个单元。
有限元模型如图3-1所示.图 3—1 转子有限元模型施加约束时，由于不考虑纵向振动与扭转振动，故约束每一节点的纵向与扭转自由度，同时约束轴承的基础节点。
施加约束后的模型如3-2所示。
图 3-2 施加约束后的有限元模型3.1 转子临界转速计算在ANSYS中可以很方便的考虑陀螺力矩的影响.考虑陀螺力矩时，由于陀螺矩阵是反对称矩阵，所以求取特征值时要用特殊的方法。
本文考虑陀螺力矩的影响，分析了在陀螺力矩的影响下,转子涡动频率随工作转速的变化趋势,其Campell图如图3-3所示。
同时给出了转子的前四阶正进动涡动频率与反进动涡动频率以及固有频率。
如表3—2所示。
表 3—2 转子涡动频率随转速的变化Ω(rpm ） 010000 20000 3000040000 1F ω（Hz ） 54。
某型涡轮转子发动机强度和转子动力学分析的开题报告
某型涡轮转子发动机强度和转子动力学分析的开题报告一、研究背景涡轮转子发动机是现代航空发动机的重要组成部分，其性能直接关系到飞机的安全、可靠和经济性。
涡轮转子发动机的强度和转子动力学分析是对其设计和优化的重要研究方向。
因此，对涡轮转子发动机强度和转子动力学的分析和研究具有很高的实际应用价值和科学意义。
二、研究目的本研究旨在通过理论分析和数值模拟的方法，对某型涡轮转子发动机的强度和转子动力学进行分析，为其设计和优化提供理论基础和实际指导。
三、研究内容1. 涡轮转子发动机的叶片和转子的强度分析和优化设计；2. 涡轮转子发动机的旋转动力学分析和振动抑制研究；3. 利用有限元仿真等数值方法对涡轮转子发动机进行动态特性分析和优化。
四、研究方法本研究主要采用理论分析和数值模拟相结合的方法，具体包括：1. 理论计算：分析涡轮转子发动机的叶片和转子的强度、刚度、动力学参数等；2. 有限元分析：建立涡轮转子发动机的有限元模型，进行强度、刚度、动力学仿真计算；3. 振动测试：采用振动测试手段获取涡轮转子发动机的动态响应特征，分析其振动特性和谐响应等参数；4. 仿真计算：通过数值模拟方法，在计算机上对涡轮转子发动机的动态响应特性进行计算和优化。
五、研究意义涡轮转子发动机的强度和转子动力学分析是对其设计和优化的重要研究方向。
通过本研究，将可以：1. 对涡轮转子发动机的叶片和转子的强度进行分析和优化设计，提高其叶片和转子的抗拉强度和抗冲击能力。
2. 对涡轮转子发动机的旋转动力学进行分析，掌握其振动和谐响应的规律，为抑制涡轮转子发动机的振动提供依据。
3. 利用有限元仿真等数值方法对涡轮转子发动机进行动态特性分析和优化，为其设计和优化提供理论基础和实际指导。
六、研究计划本研究计划分为以下几个阶段：1.文献调研、理论分析（1个月）：通过阅读相关学术论文，对涡轮转子发动机的强度和转子动力学进行理论分析，并确定研究方案和实验设计。
2.有限元分析和振动测试（2个月）：建立涡轮转子发动机的有限元模型，进行力学分析和振动测试，并获取相关数据和图表。
转子动力学
ABSTRACTThe goals of this study were to examine the dynamic force-deformation and kinematic response of a late model van subjected to an inverted drop test and to evaluate the accuracy of three-dimensional multi-point roof deformation measurements made by an optical system mounted inside the vehicle. The inverted drop test was performed using a dynamic rollover test system (Kerrigan et al., 2011 SAE)with an initial vehicle pitch of −5 degrees, a roll of +155degrees and a vertical velocity of 2.7 m/s at initial contact.Measurements from the optical system, which was composed of two high speed imagers and a commercial optical processing software were compared to deformation measurements made by two sets of three string potentiometers. The optical and potentiometer measurements reported similar deformations: peak resultant deformations varied by 0.7 mm and 3 ms at the top of the A-pillar, and 1.7mm and 2 ms at the top of the B-pillar. The top of the vehicle B-pillar sustained peak resultant deformation of 146.2 mm 116 ms after contact, and unloaded to 77.1 mm (47% of peak)at 291 ms. Peak reaction forces at contact were approximately 100 kN, and the force-deflection response between the drop test and the IIHS roof crush test on the same make and model vehicle showed comparable dynamic and quasi-static stiffness. The results presented in this study showed that the optical system can be used to measure dynamic roof deformations, in three dimensions, at high rates, across a large area of the vehicle structure, from inside a vehicle subjected to rollover crash test.INTRODUCTIONMulti-point deformation information can be an enabler in validating vehicle finite element model predictions,examining the mechanism of rollover-crash induced injuries,and studying the type of relationship between the timing,location, and magnitude of roof deformations and occupant injury metrics.Previous research has presented roof deformation measurement techniques using string potentiometers and videogrammetry during multiple rollover events [2].However, the methods are not described in detail, the results are only presented for single points, and the two techniques are not compared to each other or any other independent deformation measurement technique.The goal of this study was to evaluate the accuracy of measurements made with a three-dimensional multi-point optical deformation measurement system in a high-rate deformation experiment. The optical approach relies on the principles of stereo videogrammetry to accurately produce three-dimensional displacement time histories for a high resolution multi-point surface. Combined with vehicle kinematics and ground reaction force time histories, the optical output could provide a powerful tool for validating vehicle finite element roof structural models as well as occupant injury metrics.To achieve these goals, an inverted vehicle drop test was performed on a late model passenger van using the University of Virginia Center for Applied Biomechanics' Dynamic Rollover Test System (DRoTS) [5]. For this test, the vehicle roll drives and sled propulsion were disabled. The test parameters were chosen to mimic the loading that occurs in the IIHS roof strength evaluation (similar to the FMVSS 216test), to allow for a force-deflection comparison between dynamic and quasi-static roof loading conditions on the same make and model vehicle.Deformation measurement was focused on the passenger side roof rail between the A-pillar and B-pillar, as this was thepoint of initial roof to ground contact and anticipated locationOptical Measurement of High-Rate Dynamic Vehicle Roof Deformation during Rollover2013-01-0470Published 04/08/2013Jack Lockerby, Jason Kerrigan, Jeremy Seppi and Jeff CrandallUVA Center for Applied BiomechanicsCopyright © 2013 SAE Internationaldoi:10.4271/2013-01-0470of maximum deformation. Two methods were used to measure the three-dimensional deformation time history of the vehicle roof structure. The optical system utilized two on-board high speed imagers and optical processing software.The second method, based on string potentiometer trilateration, was implemented at two discrete points on the A-pillar and B-pillar to validate the optical system's results.The resultant and component displacements for the A-pillar and B-pillar points were compared against the optical system's output for the same locations.The optical system incorporated ARAMIS v6 2.0 (GOM Optical Measuring Techniques), a commercially available optical measurement software package. ARAMIS utilized digital images to analyze and report three-dimensional material deformations along with the surface coordinates of points, displacements and velocities, and strain values and rates.METHODS Test ConditionsThe vehicle's as tested mass was 1911.9 kg. The initial conditions for the vehicle were a pitch angle of −5 degrees (front end down), a roll angle of +155 degrees (passenger side impact), and a drop height of 0.398 m (total vertical motion of CG prior to impact), (Figure 1). This produced a 2.706 m/s vertical velocity at contact. Unpublished finite element analysis results suggested that peak reaction force from this drop height would be approximately equal to the peak force achieved in the IIHS roof strength evaluation withthe same vehicle.Figure 1. Initial vehicle orientation for the drop test The IIHS roof strength evaluation, the quasi-static test on the vehicle used for comparison, consisted of a roof crush test to one side of the vehicle. The test system utilized an upright assembly with attached loading platen fixed at 25 degrees rolland 5 degrees of pitch [4]. The vehicle roof was crushed to a minimum of 127 mm of platen displacement at a nominal rate of 5 mm/s. Force and displacement data were reported at 100Hz for the test.Vehicle PreparationThe vehicle's overall mass and wheel distributions were measured upon delivery at UVA as the test goal weight, and monitored throughout the preparation and installation process. The vehicle fluids were drained and the seats, floor liners, roof liners, and curtain airbags were removed to allow for instrumentation installation. Steel plates were bolted to the vehicle floor to act as mounting locations for instrumentation and data acquisition equipment (Figure 2). A contact strip sensor was taped on the roof in the location of anticipated initial roof-to-ground contact as a trigger. The passenger side interior structural surfaces were painted with a stochastic pattern of black dots, 6 to 12 mm diameter with approximate 40-50% coverage of the patterned area, on awhite background to accommodate the optical system.Figure 2. Instrumentation mounting plates and sensor cube installed location on the floor pan of the vehicleBalancing ProcedureThe DRoTS cradle [5], which consisted of two vertically oriented steel tubing towers at the front and rear, connected by a set of telescoping steel tubes 5″ in diameter, was installed on the vehicle to fix the location and orientation of the vehicle's roll axis relative to the vehicle (Figure 3). It is about this roll axis that the DRoTS fixture rotates the vehicle in a typical rollover crash test (disabled for this test). Once installed, the telescoping tube ran under the vehicle body from the front to the rear and the towers were oriented perpendicular to the ground. The towers of the cradle were fixed to the vehicle frame rails in the front and rear of the vehicle by removing the fascia and bumper beams and using custom hardware to rigidly connect the towers to the locations where the bumper beams interfaced with the vehicle frame rails. The cradle assembly was centered (left-right)between the bumper beam/frame rail connections at the frontand rear of the vehicle. For simplicity, the cradle was installed such that the tube was oriented parallel with the ground when the vehicle was resting on its own suspension/tires, at the curb weight condition. The DRoTS fixture was designed to hold the vehicle cradle in such a way that the vehicle roll axis was parallel to the cradle. Once the vehicle was loaded in the test fixture, the location of the roll axis relative to the vehicle and cradle was adjusted vertically until the roll axis passed through the center of gravity (CG) of the vehicle. If the vehicle CG was not aligned in the center of the frame rails (left-right) then ballast weight was added to one side to ensure alignment. At the completion of the balancing procedure, the vehicle would not continue to rotate in either direction after being manually rotated and stopped at 45degree intervals from 0 to 360 degrees. After this adjustment was completed the exact location of the roll axis could be identified from a single marker point at the very front andrear of the cradle.Figure 3. DRoTS cradle installation on front of vehicleForce and Kinematics Measurement SensorsThe vehicle was outfitted with an inertial measurement cube containing three accelerometers (Endevco 7290E-30, Meggitt Sensing Systems, San Juan Capistrano, CA) measuring accelerations about the sensor cube's local x, y, and z component directions. Additionally three angular rate sensors were included measuring angular velocities about the same local sensor cube axes (DTS ARS-1500, Diversified Technical Systems, Seal Beach, CA) for the x direction, and two (DTS ARS-300, Diversified Technical Systems, Seal Beach, CA) for the y and z directions. The sensor cube was mounted on the floor of the vehicle, on the lateral center line (Figure 2). The DRoTS roadbed was instrumented with twenty-four uniaxial load cells, spaced evenly across the surface, and oriented to measure in the vertical direction (global Z′). Two accelerometers measuring in the vertical Z′direction were mounted to the underside of the wood surfaceat the left-front corner and right-rear corner of the center section of the roadbed.Deformation Measurement SensorsThe passenger side A-pillar and B-pillar were both instrumented with a set of three string potentiometers of 2159mm maximum travel (Firstmark Model 62, Firstmark Controls, Creedmoor, NC). Two mounting plates (25 × 50mm) were constructed out of steel stock. To each plate, a single screw and a triax accelerometer were attached (Entran Triax EGAXT3, PandAuto Technology Co., Ltd). One of the two plates was mounted on the passenger-side A-pillar, at a location approximately 150 mm from the intersection of the A-pillar, roof rail, and windshield header. The second plate was mounted on the roof rail, approximately 100 mm forwardof the B-Pillar roof rail connection (Figure 4).Figure 4. B-pillar string potentiometer attachment plateThe plates were fixed to the vehicle via a single screw inserted into existing threaded holes used for mounting the rollover curtain airbags. Rotation of each plate was prevented with a sharpened screw, inserted in the plate that was tightened against the vehicle interior at the mounting location. The strings from each of three string potentiometers were attached to the screw on each of the two plates (n= 6string potentiometers). The six string potentiometers were affixed to the floor of the vehicle via rigid steel plates attached to the driver, right front passenger and second row seat mounting locations (Figure 5).Figure 5. String potentiometer mounting and orientationOptical SystemThe optical system was comprised of two high-speed imagers (NAC GX-1, NAC Image Technology, Simi Valley, CA)with 16 mm focal length ruggedized lenses (Schneider Optics, Hauppauge, NY). The imagers were fixed at a 21degree horizontal angle with respect to each other, and mounted on a rigid aluminum camera bar along with six high intensity LED, and two laser sights tracing the center pixel of each camera for visual alignment. The camera bar was bolted onto a steel framing structure that was welded into the vehicle floor at the front row seat mounting beam (Figure 6). In the mounted orientation, the cameras shared a focal intersection point 915 mm from the lenses, which was positioned 25 mm in front of the intersection of the vehicle passenger side roof rail with the windshield header (Figure 7). Sections of the roof, roof rail, A-/B-pillars, and windshield header above thepassenger seat were included in the shared field of view.Figure 6.Figure 6 (cont). Optical system components andmounting structure on the floor pan of the vehicleFigure 7. Images from the left and right cameras at t=0ms, structure undeformedCoordinate MeasurementsA coordinate measurement machine (CMM) (Titanium Arm,FARO Technologies, Lake Mary, FL) was used to determine the locations of the front and rear roll axis marker points, side door latch plates, wheel centers, the inertial measurement cube origin and orientation markers, the locations of the string potentiometer attachment screw locations on the A-/B-pillars, the points where the strings come out of the potentiometer bases, the accelerometers mounted on the string attachment plates, and four points located in the view of the optical system. Since digitizing these points required moving the CMM around the exterior of the car, a series of overlapping points were taken in each measurement location,and each point cloud captured in each measurement location was aligned in a single coordinate system by singular value decomposition [3].Data ProcessingKinematics Data ProcessingAll sensor data were filtered and debiased. Road load cells,vehicle accelerometers, and string potentiometers, were filtered to CFC60 and vehicle angular rate sensors were filtered to CFC180 [6]. For the purpose of calculating the angular accelerations necessary for determining vehicle CG kinematics from kinematics measured at the sensor cube, theangular velocity data were filtered with a Butterworth 4-pole zero-phase low-pass digital filter with a 25 Hz cutoff. Road loads were summed to determine total vertical reaction force.The time of initial vehicle to road contact was determined to within 1 ms from high speed video, and all time history data were time shifted so that t =0 corresponded with the time of initial vehicle contact with the road surface.Once the CMM data point clouds were unified, vehicle local and global (inertial) coordinate systems were defined. A standardized SAE definition for the vehicle coordinate system was used [6]. The vehicle's positive X axis was defined by a vector directed from the rear roll axis point to the front roll axis point; the positive Y axis was defined by an average of vectors connecting similar points from the driver's side to the passenger's side door latch plates; and positive Z was determined by the cross product of X and Y vectors.These vectors were calculated in the CMM coordinate system and were used to define the rotation matrix R vehcmm .The point cloud was then rotated from the CMM coordinate system to the vehicle local coordinate system by R vehcmm and its origin was translated to the center of the line connecting the front and rear roll axis marker points. The front/rear right/left weight distribution was used, with the CMM-determined locations of the center of the wheels, to determine the location of the vehicle CG on the XY plane. Then the origin of the vehicle coordinate system was translated to the CG point.The global (inertial) coordinate system was defined based on the sled system rails used to propel the roadbed. The roadbed motion was defined to travel in the positive X′ (global)direction and the Z′ axis was defined to be perpendicular to the test facility floor, with positive pointing downward. The global Y′ axis was determined by the cross product of Z′ withX′.Figure 8. Vehicle local and global (inertial) coordinatesystemsTo transform the sensor cube kinematics measurements to the vehicle local and global (inertial) coordinate systems rotation matrices defining the relationships between these frames had to be identified. The transformation between the sensor cube and vehicle local coordinate system R vehcube , which remained constant throughout the test, was determined from the set of sensor cube orientation points captured with the CMM.Sensor accelerations and angular rates were transformed to the vehicle local coordinate system by R vehcube .To calculate vehicle kinematics in the global reference frame,the time history of the transformation R globalveh relating the vehicle local system to the global system was determined.Beard and Schlick formulated a method to update the matrix R globalveh at each time step using only local frame angular velocity measurements [1]. The details of this method are presented concurrently with this study (Kerrigan et al. 2013,SAE).Before transforming the acceleration data from the sensor cube to the local coordinate system using R vehcube , the sensor accelerations were corrected for the effect of gravity. Global acceleration time histories were then calculated by transformation of vehicle frame acceleration (at the vehicle CG) time histories by the R globalveh time history. Global velocities and displacements were determined by numerical integration of the global acceleration and global velocities,respectively.String Potentiometer TrilaterationData were sampled from the potentiometers at 10 kHz during the test. At each time step, 0.1 ms increments, the three-dimensional location of the A-pillar and B-pillar attachment points were solved for using a trilateration technique. For this process it is assumed that the intersection of the three points existed on the surface of three spheres with centers fixed at the locations where the strings come out of the potentiometers. It is also assumed that those string orientation points do not move relative to the vehicle CG and coordinate system during the test. For this analysis, a potentiometer coordinate system is defined to have its origin at the location of one of the points where the string exits the potentiometer sensor. The potentiometer x axis is defined to point in the positive direction such that a second string base is at a location (d, 0,0) and the third potentiometer lies in the +xy plane at a location (i,j,0). From this the distance from each of the three pots (r1, r2, and r3) to the location of intersection ofthe three strings can be written asRearranging the equations to solve for the unknowncoordinates x, y, and z of the intersection point yieldsThe z coordinate, expressed as the positive or negative square root, can have zero, one, or two possible locations. The positive z location was chosen to locate the point above the vehicle floor. The resulting coordinate location time histories for the A-/B-pillar points were rotated into the standard vehicle coordinate system using the CCM data points.Optical System ProcessingBefore installation into the vehicle, the optical system was calibrated in the ARAMIS software using a specialized calibration object from the manufacturer (GOM Optical Measuring Techniques). A measurement volume of 1280 mm by 1280 mm by 1175 mm was produced for the test. Images were captured at 915 by 915 pixel resolution, with an average initial focal length to the structure of 915 mm. Each pixel in the image corresponds to a 1.5 by 1.5 mm square on the vehicle surface. The black dots in the paint pattern corresponded to between 4 to 8 pixels in diameter on average.The imagers recorded synchronized frames at 3000 Hz for 800ms, 100 ms before the event and 700 ms after roof-to-ground contact.The images were analyzed in ARAMIS at 1000 Hz, using every third frame in the series. ARAMIS recognizes the surface structure of the measured object in an image, and assigns 2D coordinates to the image pixels. For 3D measurements, two cameras are calibrated with the software to record synchronized images. ARAMIS uses photogrammetric methods to combine the 2D coordinates for each pixel, as observed from the left and right camera images,into a common 3D coordinate for the analysis. The software observes the deformation of the object through a series of images by discretizing each image into facets, unique square groupings of pixels, similar to finite elements used in computational analyses. The facets are identified by the gray level structure of the individual pixels within the facet. The software tracks the changing location of each facet throughout the image series to calculate the displacements and strains of the object's surface. The pixel size of each facet and the pixel step, overlapping area of adjacent facets, can be adjusted in the software and manually optimized for the analysis conditions including image resolution, geometric complexity of measured object, and desired resolution of the resulting strain and displacement fields. In order for the software to divide the images into recognizable facets, there must be sufficient variation of pixel gray scale on the object'ssurface. Surfaces that are heterogeneous in color require the application of a stochastic paint spray or dot pattern to produce pixel variation.A facet size of 20 pixels and a facet step of 10 pixels were used in the analysis. This provides an output of individually calculated points in a 10 by 10 pixel grid, equivalent to every 15 mm on the physical surface. Using the physical coordinate locations captured by the CMM and their corresponding locations in the ARAMIS software coordinate system, a transform was applied to the optical output to align it with the SAE vehicle coordinate system.RESULTSForce and KinematicsThe peak sum total vertical force recorded by the roadbed was 98,754 N at 40.5 ms after touchdown (Figure 9). After the initial peak, the force time history shows oscillatory behavior of approximately 3 Hz, centered around 19,000 Nwhich corresponds to the weight of the vehicle.Figure 9. Roadbed sum total vertical forceThe peak resultant global vehicle CG acceleration was 7.8 g at 10.9 ms (Figure 10). The peak for global X′ acceleration was 7.2 g at 11.0 ms, the global Y′ was 4.1 g at 14.9 ms, and the global Z′ acceleration was −6.9 g at 24.8 ms. Global velocity resultant reached a maximum of 2.87 m/s at 15.8 ms.The peak global Z′ velocity was 2.83 m/s at 9.4 ms (Figure 11). Global resultant displacement had a maximum of 0.566m at 121.4 ms (Figure 12). The peak global Z′ displacement was 0.563 m at 121.7 ms.Figure 10. Vehicle CG global accelerationsFigure 11. Vehicle CG global velocitiesFigure 12. Vehicle CG global displacementsThe maximum acceleration measured at the B-pillar was 31.1g at 5.5 ms after impact, and at the A-pillar was 15.7 g at 7.4ms (Figure 13). The accelerometers measure approximately 1g before t=0, as the vehicle is falling under gravity.Figure 13. Resultant Acceleration at A-/B-PillarsRoof Deformation MeasurementThe peak resultant deformation reported by the optical system was 146.5 mm at the top of the B-pillar 116 ms after contact (Figure 14). The structure subsequently unloaded to a minimum resultant deformation value of 77.1 mm at 291 ms (Figure 15). This accounted for a 47.3% rebound, normalizedby the peak deformation.Figure 14. ARAMIS resultant displacement overlaid onto left camera image at t=116ms, maximum 146.2 mmFigure 15. ARAMIS resultant displacement overlaid onto left camera image at t=291ms, maximum 77.1 mm The maximum resultant deformation at the A-pillar was 87.9mm at 123 ms reported by the optical system, and 88.6 mm at 121 ms reported by the string potentiometers (Figure 16). At the time of peak resultant, the component deformations reported by the optical system were −20.9 mm in the X,−81.4 mm in the Y, and 25.3 mm in the Z directions. The string potentiometers reported −48.6 mm in the X, −73.5 mmin the Y, and 9.5 mm in the Z directions.Figure 16. A-Pillar displacement comparison betweenString Potentiometers and ARAMIS outputThe maximum resultant deformation at the B-pillar was 146.2mm at 112 ms reported by the optical system, and 145.0 mm at 114 ms reported by the string potentiometers (Figure 17).At the time of peak resultant, the component deformations reported by the optical system were −24.1 mm in the X,−134.2 mm in the Y, and 52.8 mm in the Z directions. The string potentiometers reported −27.7 mm in the X, −132.3mm in the Y, and 52.4 mm in the Z directions. The 3 Hz oscillation is also present in the roof deformationmeasurements at the A-/B-pillars.Figure 17. B-Pillar displacement comparison betweenString Potentiometers and ARAMIS output The vehicle exhibited elastic rebound effects captured by the optical system (Table 1). The unloaded displacement values are taken from t=291ms when the first deformation minimum occurs after contact. The normalized rebound values are calculated by dividing the amount of deformation rebound (peak minus minimum) by the peak deformation.Table 1. Optical displacements at the A-/B-pillars for times of maximum deformation and maximumunloadingForce-DeflectionThe maximum total sum force measured during the test at the roadbed of 98,754 N was reached at 48 mm of resultant deformation for the A-pillar, 67.5 mm of resultant deformation for the B-pillar, and at 96 mm of global vertical displacement of the vehicle's CG following initial roof-to-ground contact (Figure 18). The maximum force reached in the IIHS roof crush test for this same vehicle was 100,617 Nat 85 mm of platen deformation.Figure 18. Force vs Deflection curves for the A-/B-Pillar resultants, CG global vertical Z displacement, and IIHSroof crush testDISCUSSION Optical SystemTo successfully implement the optical deformation measurement technique on-board a dynamic test, the calibration and focal intersection of the stereo imagers must be maintained throughout image capture. With peak accelerations of around 8 g, it was imperative that the cameras be rigidly fixed with respect to each other as any divergent motion between the two cameras can cause error or total loss of results. A rigid connection to stiff structural members in the vehicle frame was designed to prevent rigid body motion of the camera beam with respect to the measured surfaces. In this test, the optical system maintained calibration between the two imagers during the vehicle-to-ground impact acceleration spike and subsequent vibrations.The nominal intersection deviation between the two imagers calculated by ARAMIS was 0.8 pixels, and did not change significantly during the impact. Some areas of complex geometry on the hat section roof stiffeners, and areas ofsignificant buckling on the roof sheet were not tracked throughout the entire deformation.Although the images were recorded at 3000 Hz during the test, they were processed at 1000 Hz in ARAMSIS to reduce computational expense and post processing effort. Due to the limited size of the ruggedized lenses used there was significant vignetteing of the images (Figures 7, 14, 15). The partially blocked view interfered with the software's ability to automatically match facets between the left and right images,requiring manual pairing for each time increment. Future tests should utilize the full image sensor chip to increase resolution and accuracy, while avoiding manual post processing. This was a limitation of the current study;however, it appears that 1000 Hz is sufficient to capture the fast rate deformation of a vehicle roof during an inverted ground contact.Deformation Measurement ComparisonThe string potentiometer attachment locations on the A-/B-pillars were chosen to be the existing curtain airbag tapped holes to minimize the installation's impact on vehicle structure. Due to geometric constraints on the vehicle interior,the string potentiometers were not mounted orthogonally in line with the vehicle coordinate axes, but rather to maximize the angle between the three strings to improve the accuracy of the trilateration technique (Figure 5). Orthogonal alignment is not necessary when utilizing trilateration; however it is imperative that the potentiometer bases are rigidly mounted to the vehicle structure so that they remain fixed in the vehicle coordinate system, and are assumed to not move relative to the vehicle CG. High speed video of the string potentiometers refuted concerns of string oscillations impairing the calculation, as only slight vibrations are apparent in the video and do not translate into the collected data signal. The oscillations in the string potentiometer signal (Figures 16, 17) are present before the drop initiates when the strings are not moving, and are attributed to signal noise.The deformation time histories of the optical system and string potentiometer trilateration correlated well (Figures 16,17). The resultant displacements at the A-/B-pillars for the two techniques matched almost exactly, reporting a difference in peak deformation of 0.7 mm and 2 ms at the A-pillar, and a 1.2 mm and 2 ms at the B-pillar. The B-pillar component displacements were in good agreement between the two methods with the maximum difference of 13%occurring in the X direction.Component Disagreement and Ongoing TestingThe lack of A-pillar component agreement was at first hypothesized to be related to a coordinate transformation error in the string potentiometer processing, as the resultant matched closely and the X and Y directions were in phase but。
转子动力学大作业
转子动力学大作业学院：姓名：班级：学号：目录一、作业题目介绍二、转子动力学理论简介三、参数的选择和计算四、Ansys分析临固有频率和临界转速五、失稳转速影响因素及计算一、大作业题目1、 计算临界转速；2、 圆轴承，长颈比为0.8，油膜间隙2‰3、 计算失稳转速注：转子两端各一个轴承，支点在左右两端。
二、转子动力学理论知识由于制造中的误差，转子各微段的质心一般对回转轴线有微小偏离。
因此，当转子转动时，会出现横向干扰，在某些转速下还会引起系统强烈振动，出现这种情况时的转速就是临界转速。
为保证系统正常工作或避免系统因振动而损坏，转动系统的转子工作转速应尽可能避开临界转速，若无法避开，则应采取特殊防振措施。
这也是研究临界转速的意义。
临界转速和转子不旋转时横向振动的固有频率相同，也就是说，临界转速与转子的弹性和质量分布等因素有关，n kmω=。
当圆盘不装在两支撑的中点而偏于一边时，转轴变形后，圆盘的转轴线与两支点A 和B 的连线有一夹角ψ。
设圆盘的自转角速度Ω，极转动惯量为p J ，则圆盘对质心o '的动量矩为 p H J =Ω。
它与轴线AB 的夹角也应该是ψ，见图1。
当转轴有自然振动时，设其频率为n ω，则圆盘中心o '与轴线AB 所构成的平面绕AB 轴有进动角速度n ω。
由于进动，圆盘的动量矩H 将不断改变方向。
因此有惯性力矩()g n n p n M H H J ωωω=-⨯=⨯=Ω⨯方向与平面o AB '垂直，大小为sin g p n M J ωψ=Ω1800mm980mm 8040170170100 转子结构尺寸示意图轮盘轮盘轮盘这一惯性力矩称为陀螺力矩或回转力矩。
因夹角ψ较小，sin ψψ≈，上式可写作g p n M J ωψ=Ω。
这一力矩与ψ成正比，相当于弹性力矩。
在正进动(0/2ψπ<<)的情况下，它使转轴的变形减小，因而提高了转轴的弹性刚度，即提高了转子的临界角速度。
水轮机转子动力学分析
B.水轮机的安装位置
C.水轮机的材料
D.水轮机的功率
11.在进行水轮机转子动力学分析时，以下哪个步骤是必要的？（）
A.确定转子的几何尺寸
B.确定转子的临界转速
C.确定转子的质量分布
D.所有以上步骤
12.以下哪个方法通常用于测量水轮机转子的振动参数？（）
A.位移传感器
B.麦克风
C.红外线传感器
8.在所有情况下，增加轴承的刚度都能降低转子的振动。（）
9.水轮机转子的不平衡是导致其振动的主要原因。（）
10.对于水轮机转子动力学问题，只需要关注转子的线性振动特性。（）
第四部分主观题（本题共2小题，每题10分，共20分）
1.请简述水轮机转子临界转速的重要性，并说明如何通过改变转子的结构参数来调整临界转速。（10分）
A.转子的固有频率与强迫频率相等
B.转子的固有频率与强迫频率相差很大
C.水流频率与转子固有频率相等
D.外部激励频率与转子固有频率相等
14.以下哪些措施可以用于防止水轮机转子产生过度振动？（）
A.定期对转子进行平衡
B.优化轴承的支撑结构
C.控制水轮机的运行参数
D.所有以上措施
15.以下哪些条件有助于提高水轮机转子的动态平衡？（）
A.转子的质量分布均匀
B.转子材料的一致性
C.轴承的准确安装
D.转子的精确加工制造
第三部分判断题（本题共10小题，每题2分，共20分，正确的请在答题括号中画√，错误的画×）
1.水轮机转子动力学分析主要关注转子的静态特性。（）
2.在水轮机转子振动分析中，临界转速是指转子开始出现不稳定振动的最低转速。（）
D.激光传感器
13.在水轮机转子动力学分析中，以下哪个参数表示振动频率？（）
SAMCEF有限元转子动力学分析实例
第15章转子动力学分析实例15.1转子动力学理论背景15.1.1 概述带有旋转部件的整体结构，比如说飞机引擎，它的动力学行为分析需要旋转部件、定子部件和不同的连接设备的模型。
模型的处理过程采用的是有限元方法.为了评估系统的整体动力学性能,在对系统的主要方程进行表述之后也要对其进行不同的分析。
这些分析类型主要如下:▪转子系统的临界转速计算；▪当系统中包含控制设备时，检查在旋转速度范围内的稳定性也是必要的;▪叶片丢失等不平衡引起的振动量级预测。
主要的假定有以下方面.首先，结构元件的振动水平保持弹性和几何线性行为,也就是说转子和定子都假定是线弹性的。
非线性行为主要是局部的并且存在于模型装配时。
另一方面,有足够能量去获得需要的旋转速度。
由于弹性的定子对系统的响应有很大的影响，并且这些结构大多数不是轴对称结构，所以系统用惯性坐标系来描述。
15.1.2 转子有三种有限元模型可用来描述转子系统。
1D模型：转子用梁、弹簧和集中质量单元来模拟,这个模型计算速度快,它适用于有大量参数需要调整时的初期设计分析。
但是，比如前文提到的飞机引擎，这个模型的细节可能需要许多专业的经验还有可能耗费很多时间。
图2.1 梁-弹簧-集中质量模型傅立叶模型：转子采用2D傅立叶多谐波单元模拟.对于转子动力学方面的应用,为了描述轴向变形、扭矩变形和弯曲变形与陀螺力矩耦合,必须考虑0和1节径的谐波。
这种模型允许旋转设备的更精细模型的开发，它非常适合于带有多数目叶片的旋转机械的建模，也适合圆锥杆的更好的建模307308图2。
2 2D 傅立叶转子模型为了促进轴对称转子模型和与它耦合的固定部件或其它旋转部件的使用，还要考虑陀螺效应和阻尼的影响，更新了多谐波实体单元和壳单元库。
为了考虑转子的离心刚度，同时采用不同谐波是一个简单的方法，在瞬态分析中，它可以在同样的运行中做到。
另一方面,单元库包含一种专门的连接单元，这种单元可以考虑3D 模型和傅立叶模型之间或轴上的一个3D 节点和傅立叶模型之间的耦合。
ANSYS转子动力学分析
附着在旋转结构上y 的 (O'X'Y'Z')
Y’
P r’ P’
r
X’
Stationary Frame o
R
Z’ Rotating Frame
x
z
转子动力学分析的基本方程
Dynamic equation in rotating reference frame
M{&u&r}+ ⎡ ⎤
⎢⎥ ⎢⎥ ⎢⎣ ⎥⎦
( C⎡ ⎤ ⎢⎥ ⎢⎥ ⎢⎣ ⎥⎦
+[Ccor
]){u& r}+
( K⎡ ⎢ ⎢ ⎢⎣
⎤ ⎥ ⎥ ⎥⎦
−[Kspin
]){ur}=
F⎧ ⎫
⎪⎪ ⎨⎬ ⎪⎩ ⎪⎭
Coriolis force {fc}=[Ccorio]{u& r}
Coriolis matrix [Ccor]= 2 ∫ ρΦT ωΦ dv,
Campbell Diagram
• 对应不同的角速度，在模态分析中采用多载荷步对应 不同的角速度 ω, Campbell 图表现出固有频率随转动 频率的变化。
• 命令: PLCAMP, PRCAMP, CAMPB
– PLCAMP: 绘制 Campbell diagram – PRCAMP: 输出频率和临界转速 – CAMPB: 支持预应力结构的Campbell图计算
⎤⎧u& ⎥⎦⎨⎩u&
x y
⎫ ⎬ ⎭
+
⎡K ⎢⎣K
fxx fyx
K fxy K fyy
⎤ ⎥ ⎦
⎧u ⎨⎩u
转子动力学作业模板
1、模态分析对例题一进行建模，作模态分析。
2、谐分析(幅频，相频)幅频相频2个盘相位相差180°，峰值的临界转速和坎贝尔图相吻合。
3、一阶振型，二阶振型4、弹性支撑转子弹簧阻尼单元COMBI214，由两个节点组成，每个节点有两个自由度，不考虑弯曲和扭转。
4个刚度系数，主刚度和交叉刚度。
4个阻尼系数。
（1）有/无阻尼情况下无阻尼的情况下：临界转速118.529 rad/s在考虑弹簧阻尼情况下时，即改变combi214单元中4个阻尼系数，但是得到的临界转速结果与无阻尼时相同，具体原因没有得出。
（2）考虑滑动轴承的轴颈弯曲之前是通过在对应节点施加COMBI214单元来进行考虑的。
动力系数的设置则是通过对Sommerfeld数的计算，这样操作的合理性是基于以下假设：动力系数可看作常数；所计算轴承Sommerfeld数与动力系数的关系；轴承很短，可以忽略轴承中轴颈的弯曲变化；但是实际轴承都具有一定的宽度，所以，可以通过在轴承上连续几个节点上施加COMBI214单元来对滑动轴承中的轴颈弯曲进行考虑。
所建模型如下：(a)单个节点(b)三个节点通过对Sommerfeld数的计算，查表估算了相同数量级的一组动力系数进行计算，又考虑实际轴承油膜力沿轴向分布近似抛物线，所以对中间节点采用了较大的动力系数，而边上两个节点动力系数则取中间节点动力系数的一半。
计算结果如下表所示，为利用不同节点数考虑滑动轴承得到的计算结果：轴承节点数一阶固有频率（rad/s)二阶固有频率（rad/s)三阶固有频率（rad/s)174.63875.354263.875376.69981.945273.507可以看出，当采用多节点来模拟滑动轴承，所施加约束介于固支和铰支之间，所计算得到固有频率升高。
(b)三个节点通过（a）（b）的幅频响应图可以看出，当采用三节点进行模拟时，幅值降低，固有频率增大。
通过利用多节点来模拟滑动轴承由于考虑了轴在轴承部分的弯曲，计算结果应该更加合理，。
转子动力学作业(传递矩阵法)
%求解转子系统前三个临界转速和主振型的传递矩阵法clcclear%等截面轴参数l1=0.12;d=0.04;A=pi*d*d/4;%轮盘参数D=0.5;h=0.025;%盘轴材料参数（忽略轴的质量）a=1;u=0.3;rou=7800;E=2.0e11;G=E/(2*(1+u));I=pi*(d^4)/64;K1=2.0e7;v1=6*E*I/(a*G*A*l1*l1);mi=rou*pi*D^2/4*h;%轮盘的集质量Jp=mi*D^2/8; Jd=Jp/2;Ji=Jp-Jd;%参数的数组形式L=[l1 l1 l1 l1 l1 l1 l1 l1 l1 l1 l1 l1 l1 0 0];M=[0 mi mi mi mi mi mi 0 0 0 0 0 mi mi 0];K=[K1 0 0 0 0 0 0 K1 0 0 0 K1 0 0 0];v=[v1 v1 v1 v1 v1 v1 v1 v1 v1 v1 v1 v1 v1 0 0];J=[0 Ji Ji Ji Ji Ji Ji 0 0 0 0 0 Ji Ji 0];k=0;Tit=['第一阶频率的振型和弯矩图';'第二阶频率的振型和弯矩图';'第三阶频率的振型和弯矩图'];for w=0:0.01:4000;for i=1:15;T(:,:,i)=[1+(L(i)^3)*(1-v(i))*(M(i)*w^2-K(i))/(6*E*I) L(i)+L(i)^2*J(i)*w^2/(2*E*I) L(i)^2/(2*E*I) L(i)^3*(1-v(i))/(6*E*I);(L(i)^2)*(M(i)*w^2-K(i))/(2*E*I) 1+L(i)*J(i)*w^2/(E*I) L(i)/(E*I) L(i)^2/(2*E*I);L(i)*(M(i)*w^2-K(i)) J(i)*w^2 1 L(i);M(i)*w^2-K(i) 0 0 1];endH=T(:,:,1);for i2=2:15;H=T(:,:,i2)*H;endF=H(3,1)*H(4,2)-H(3,2)*H(4,1);if F*(-1)^k < 0 %求解临界转速k=k+1;wi(k)=w;w=wi(k)ni(k)=wi(k)*30/pi;endendfor i1=1:3;w=wi(i1);for j=1:14;T(:,:,j)=[1+(L(j)^3)*(1-v(j))*(M(j)*w^2-K(j))/(6*E*I) L(j)+L(j)^2*J(j)*w^2/(2*E*I) L(j)^2/(2*E*I) L(j)^3*(1-v(j))/(6*E*I);(L(j)^2)*(M(j)*w^2-K(j))/(2*E*I) 1+L(j)*J(j)*w^2/(E*I) L(j)/(E*I) L(j)^2/(2*E*I);L(j)*(M(j)*w^2-K(j)) J(j)*w^2 1 L(j);M(j)*w^2-K(j) 0 0 1];endH=T(:,:,1);for j=2:15;H=T(:,:,j)*H;endb=-H(4,1)/H(4,2);X(:,1)=([1 b 0 0]');for n=2:16;X(:,n)=T(:,:,n-1)*X(:,n-1); %相邻两质点右边的传递关系endfor j1=1:15;y(j1)=X(1,j1);z(j1)=X(3,j1);x(j1)=(j1-1)*l1;endy(16)=X(1,16);x(16)=1.56;z(16)=X(3,16);y=y/max(abs(y));%归一化z=z/max(abs(z));subplot(3,1,i1)plot(x,y,'b-',x,z,'r:')title(Tit(i1,:))xlabel('轴长'),ylabel('不平衡值')axis([0,1.56,-1.2,1.2])grid onz;endlegend('振型','弯矩') ni wi0.511.5-101第一阶频率的振型和弯矩图轴长不平衡值00.511.5-101第二阶频率的振型和弯矩图不平衡值0.511.5-101轴长不平衡值ni = 1.0e+004 *0.1468 0.2065 0.5254 1.3837 2.3759 2.3832 3.1036 3.5473 wi = 1.0e+003 *0.1537 0.2162 0.5502 1.4490 2.4881 2.4956 3.2501 3.7147%转子系统的不平衡响应clc clearww=[153.68 216.23 550.22 1449 2488.1 2495.6 3250.1 3714.7] %前8阶固有频率 n=ww*30/pi %前8阶转频 wi=[0.9*ww(1) (ww(1)+ww(2))/2] %0.9w(1)和（w(1)+w(2))/2） %等截面轴参数 l1=0.12; d=0.04;A=pi*d*d/4; %轮盘参数 D=0.5;h=0.025;%盘轴材料参数（忽略轴的质量） rou=7800;E=2.0e11;I=pi*(d^4)/64;K1=2.0e7;m=rou*pi*D^2/4*h;%轮盘的集质量Jp=m*D^2/8; Jd=Jp/2;J1=Jp-Jd;u1=0.8e-4;%参数的数组形式L=[l1 l1 l1 l1 l1 l1 l1 l1 l1 l1 l1 l1 l1 l1];M=[0 m m m m m m 0 0 0 0 0 m m];K=[K1 0 0 0 0 0 0 K1 0 0 0 K1 0 0];J=[0 J1 J1 J1 J1 J1 J1 0 0 0 0 0 J1 J1];Tit=['wi(1)时的振动响应图';'wi(2)时的振动响应图'];U=[0 0 0 0 0 0 0 0 0 0 0 0 0 u1];for i=1:2w=wi(i);n(i)=w*30/pifor j=1:14;T(:,:,j)=[1+(L(j)^3)*(M(j)*w^2-K(j))/(6*E*I) L(j)+L(j)^2*J(j)*w^2/(2*E*I) L(j)^2/(2*E*I) L(j)^3/(6*E*I) L(j)^3/(6*E*I)*U(j)*w^2; (L(j)^2)*(M(j)*w^2-K(j))/(2*E*I) 1+L(j)*J(j)*w^2/(E*I) L(j)/(E*I) L(j)^2/(2*E*I) L(j)^2/(2*E*I)*U(j)*w^2; L(j)*(M(j)*w^2-K(j)) J(j)*w^2 1 L(j) L(j)*U(j)*w^2; M(j)*w^2-K(j) 0 0 1 U(j)*w^2;0 0 0 0 1];endG=T(:,:,1);for j1=2:14;H=T(:,:,j1)*G;G=H;endD1=H([3 4],[1 2]);B=H([3 4],[5 2]);B(:,1)=-B(:,1);C=H([3 4],[1 5]);C(:,2)=-C(:,2);b=det(B)/det(D1); c=det(C)/det(D1);X(:,1)=([b c 0 0 1]');for n=2:14;X(:,n)=T(:,:,n-1)*X(:,n-1); %相邻两质点右边的传递关系endy(1)=X(1,1);x(1)=0;for j2=2:13;y(j2)=X(1,j2);x(j2)=x(j2-1)+L(j2-1);endy(14)=X(1,14);x(14)=1.56;xi=0:0.05:1.56;yi=interp1(x,y,xi,'spline'); subplot(2,1,i)plot(xi,yi, 'b-o','LineWidth',1.5) title(Tit(i,:))xlabel('轴长'),ylabel('不平衡值') grid on end00.20.40.60.81 1.2 1.4 1.6-6wi(1)时的振动响应图轴长不平衡值00.20.40.60.81 1.2 1.4 1.6x 10-6wi(2)时的振动响应图轴长不平衡值ww = 1.0e+003 *0.1537 0.2162 0.5502 1.4490 2.4881 2.4956 3.2501 3.7147n = 1.0e+004 *0.1468 0.2065 0.5254 1.3837 2.3760 2.3831 3.1036 3.5473wi = 138.3120 184.9550n = 1.0e+003 * 0.0150 1.76620.20.40.60.81 1.2 1.41.6-101第一阶频率的振型和弯矩图轴长不平衡值0.20.40.60.81 1.2 1.41.6-101第二阶频率的振型和弯矩图不平衡值0.20.40.60.811.21.41.6-101轴长不平衡值0.511.5-101第一阶频率的振型和弯矩图轴长不平衡值0.511.5-101第二阶频率的振型和弯矩图不平衡值0.511.5-101轴长不平衡值0.511.5-101第一阶频率的振型和弯矩图轴长不平衡值0.511.5-101第二阶频率的振型和弯矩图不平衡值0.51 1.5-101轴长不平衡值00.20.40.60.81 1.2 1.4 1.6x 10-6wi(1)时的振动响应图轴长不平衡值00.20.40.60.81 1.2 1.4 1.6-6wi(2)时的振动响应图轴长不平衡值00.20.40.60.81 1.2 1.4 1.6x 10-6wi(1)时的振动响应图轴长不平衡值00.20.40.60.81 1.2 1.4 1.6-6wi(2)时的振动响应图轴长不平衡值。
某汽轮机转子动力学分析
某汽轮机转子动力学分析作者：胡雯婷刘嘉一盛锋来源：《科技视界》2016年第05期【摘要】为了获得某汽轮机转子-轴承系统的动力学特性，并验证其可靠性。
采用有限元法，通过对汽轮机转子-轴承系统进行等效简化，建立了汽轮机转子-轴承系统动力学分析模型，在此模型上对汽轮机转子-轴承系统进行转子动力学分析，包括模态分析、临界转速计算以及不平衡响应分析，分析结果表明该转子-轴承系统结构临界转速安全裕度满足要求，转子系统选取的平衡量具有较小的振动幅值，转子-轴承系统设计具有合理性，并对转子-轴承系统安全运行提供了实时监测的依据。
【关键词】转子动力学；临界转速；不平衡响应0 引言随着现代工业的发展，汽轮机的发展非常迅速，转速越来越快，效率也得到很大的提高。
当汽轮机在运转时，转子系统常常会因为发生振动而产生噪声，使转子的工作效率降低，甚至发生失稳，引发安全事故[1]，因此在汽轮机的设计之前，对转子动力学进行分析研究，就具有重要的理论意义和实用价值[2]。
应用ANSYS有限元分析软件对某汽轮机转子-轴承系统进行了动力学分析，包括模态分析、临界转速计算以及不平衡响应分析。
验证了其在设计上的合理性。
1 分析方法转子动力学以转子横向振动为主要研究对象，对旋转机械转子系统的动力学特性进行研究。
主要的求解方法有传递矩阵法和有限元法。
本文采用有限元方法进行分析。
转子的动力平衡方程[2]为：[M]{？譈}+（[G]+[C]）{？簪 }+[K]{U }={ f }（1）式中：[M]—质量矩阵，[G]—陀螺阻尼项，[C]—阻尼矩阵，[K]—结构刚度矩阵，{？譈 }—加速度向量，{？簪 }—速度向量，{U }—位移向量。
2 转子动力学分析2.1 计算模型某汽轮机转子-轴承系统由主轴、叶轮和轴承组成，根据转子-轴承系统之间的关系，并按照质心不变原则，对其进行简化，将主轴、叶轮、叶片简化为阶梯转轴、圆盘和支承[3]。
将主轴模拟成三维梁单元（BEAM188），叶轮模拟成质量单元（MASS21），轴承模拟成二维弹簧-阻尼单元（COMBI214）。
转子动力学报告
图 1 单圆转子系统模型
2 转子宽度对转子临界转速的影响
为了探究转子宽度 b 对临界转速的影响，对 b=0,10,21,30 进行了分析。选用 有限元模型，计算单元采取质量单元 Mass21，粱采取 Beam188，推导得出极转 动惯量 J p 和绕直径转动惯量 J d 如下：
i ( t + )
，
z x iy 。对转子系统 1 =
如下图。
6
, 2 =
=2501/ s 范围内进行求解，结果 3 ，在转速
图 6 圆盘 1 中心 圆盘 2 中心 x,y 方向位移振幅与激励关 系
图 8 圆盘 1 中心 x,y 方向相位与激励频率关系
k11 k22 krr , k33 k44 k k14 k41 k23 k32 kr k r
，特征频率方程为
4n ( J p / J d )n3 (rr 2 2 )n 2 ( J p / J d )rr 2n rr 2 2 r 2r 2 0 （2）
b> 3R 时， J d J p ，二阶正涡动曲线斜率小于 1，和 n = 有交点，出现四阶临
界转速。但是工业中用到的单元盘转子大部分振动是因为不平衡量引起的，而不 平衡量引起的振动中，轴心轨迹都是正进动，因而临界转速最多只有两阶，一阶 临界转速 'c1 c 2 ，二阶临界转速 'c 2 c 4 。 同时对轴和圆盘都采用梁单元 Beam188 进行计算，与上面进行对比，探究 网格类型对计算结果影响，计算结果表 2。比较表 1,2 可知考虑了圆盘结构，采 用单元梁单元计算结果中临界转速要比同条件下质量单元计算结果大一些， 比较 m=20kg 下计算结果，质量单元计算结果和理论结果很接近，看似梁单元计算错 误， 其实是计算模型中将圆盘看做薄圆盘简化为一质量质点所致，其实计算中还 因考虑圆盘抗弯刚度 EI 以及宽度 b。从表 2 和图 3（b）可以看出，增加 b 到一 定长度（21cm）时，会出现二阶临界转速。这和质量单元讨论结果一致。但是 与质量单元计算结果不同的是， 一阶临界变化趋势是随着宽度 b 增加，一阶临界 转速 'c1 c 2 先减小后增大，这主要是因为开始时增加 b 占主要作用，而圆盘 刚度占次要作用，因而 'c1 呈下降趋势，而当增大到一定程度时，圆盘刚度占主 要作用，因而会出现 b=30cm 时的一阶临界转速反而比 b=21cm 时大。从上面分 析可知， 圆盘宽度较小时即薄圆盘时用质量单元计算误差范围可以接受，但是当 宽度较大时则需要使用梁单元或者分段使用质量结点。 基于以上分析，对于高速转子，应尽可能减小宽径比（b/R） ，使得 J d J p ， 抑制二阶临界转速出现， 同时计算时对于宽度较大时的转子应该采用梁单元进行 计算。
newmark-β法求解转子动力学
主题：newmark-β法求解转子动力学内容：1. 转子动力学是动力学领域的一个重要分支，研究转子系统在运转过程中的振动特性和稳定性。
2. 在转子动力学的研究中，求解转子系统的运动方程是一个重要的问题。
传统的方法包括有限元法、模态叠加法等，但随着计算机技术的发展，数值方法在转子动力学中的应用越来越广泛。
3. newmark-β法是一种常用的数值求解转子动力学问题的方法，它是一种基于有限差分的算法，能够较为准确地求解非线性动力学问题。
4. newmark-β法的基本思想是将转子系统的运动方程离散化，然后利用迭代的方式求解离散化的方程组。
其优点在于能够处理非线性效应和耗散效应，适用于各种转子系统的振动分析。
5. 在应用newmark-β法求解转子动力学问题时，需要首先建立转子系统的数学模型，包括转子的几何形状、材料性质、支承刚度等参数，然后对转子系统进行离散化处理，得到离散化的运动方程。
6. 在进行数值求解时，需要选取适当的时间步长和迭代次数，以保证求解的准确性和稳定性。
需要对新马克-β方法的参数进行合理的选择，以获得最佳的求解效果。
7. newmark-β法求解转子动力学问题的过程中，还需要对边界条件和初始条件进行合理的设定，以保证求解的可靠性。
对于一些特定的问题，还需要进行稳定性分析和收敛性分析，以评估方法的适用性。
8. 在实际工程中，newmark-β法已经被广泛应用于求解各种转子动力学问题，例如离心压缩机、涡轮机等。
其准确性和高效性得到了工程界的认可和广泛应用。
结论：通过对newmark-β法求解转子动力学的方法和过程进行研究和探讨，我们可以发现该方法具有一定的适用性和实用性，能够帮助工程师和研究人员更好地理解和分析转子系统的振动特性和稳定性，为工程实践提供可靠的数值模拟和分析手段。
然而，对于一些复杂的非线性和耗散问题，仍需要进一步研究和改进该方法，以满足工程实际应用的需求。
希望在未来的研究中，能够进一步优化和推广newmark-β法，为转子动力学问题的分析和求解提供更加可靠和高效的计算方法。
转子动力学
利用传递矩阵法和Riccati 传递矩阵法分析转子临界转速 例2.1(P68)：利用传递矩阵法和Riccati 传递矩阵法求解如图所示的转子临界转速，计算要考虑转轴的质量（ρ=7800kg/m 3）转子简化如下图所示：转子由三个支座，三个轮盘，一个铰链分成等截面的六段相关参数如下：三个圆盘的参数为：{m 1=3.5kg,m 2=7kg,m 3=3kgI p1=0.016kg ∙m 2,I p2=0.05kg ∙m 2,I p3=0.016 kg ∙m 2I d1=0.012kg ∙m 2,I d2=0.025kg ∙m 2,I d3=0.012 kg ∙m 2阶梯轴的三段轴的截面惯性矩分别为：{J 1=1.7 cm 4J 2=3.2 cm 4J 3=0.9 cm 4轴材料的弹性模量为：E =2×1011N/m 4求得三段长轴的单位质量分别为:{ m L1=2.45 kg m ⁄m L2=3.06 kg m ⁄m L3=1.59 kg m ⁄ 情况一（不考虑支撑刚度）：A ：传递矩阵法一、 试算各段转轴的传递矩阵取试算转速p=ω=1500 rad s⁄ ; 则各轴段的传递矩阵分别为：第1段{l=0.06 mJ=1.7×10−8 m4 m L1=2.45 kg m⁄p=1500rad/s ; H1=[10.060.058415.29e−7 1.06e−81.77e−5 5.29e−79.92e31983.31e59.92e31 0.060.0584 1]第2段{l=0.15 mJ=3.2×10−8 m4 m L2=3.06 kg m⁄p=1500rad/s ; H2=[10.150.60611.76e−68.79e−82.35e−5 1.76e−67.76e4 3.88e31.04e67.76e41 0.150.606 1]第3段{l=0.05 mJ=3.2×10−8 m4 m L2=3.06 kg m⁄p=1500rad/s ; H3=[10.050.022411.95e−7 3.26e−97.81e−6 1.95e−78.61e31433.44e58.61e31 0.050.0224 1]第4段{l=0.03 mJ=3.2×10−8 m4 m L2=3.06 kg m⁄p=1500rad/s ; H4=[10.034.84e−317.03e−87.03e−104.69e−67.03e−83.10e331.02.07e53.10e31 0.034.84e−3 1]第5段{l=0.1 mJ=0.9×10−8 m4 m L3=1.59 kg m⁄p=1500rad/s ; H5=[10.10.33112.78e−69.26e−85.57e−5 2.78e−61.79e45963.58e5 1.79e41 0.10.331 1]第6段{l=0.06 mJ=0.9×10−8 m4 m L3=1.59 kg m⁄p=1500rad/s ; H6=[10.060.071611.00e−62.00e−83.33e−5 1.00e−66.44e31292.15e5 6.44e31 0.060.0716 1]此6段传递矩阵均采用MATLAB编程求解，MATLAB的源文件为zhouduan.m二、采用传递矩阵法进行各段轴的状态参数的传递初始参数列阵为：[X01θ01M01 Q01]=[X01θ01−(1−ωPI pI d)I d p2θ01m1p2X01]令X01=1，则初始矩阵可化为：[1θ019000θ017.875e6]以初始矩阵乘第一轴段的传递矩阵，则可得第一段轴的终端状态参数：[X k1θk1M k1 Q k1]=[1.08+0.065θ014.23+1.16θ014.825e5+9.206e3θ018.21e6+1.045e3θ01]根据X k1=0可计算得：θ01=−16.739；则，可得支座A后第2段的起始端参数阵为：[X02θ02M02 Q02]=[−15.1853.28e58.038e6−R A]其中，R A为刚性支座的反作用力；用第2段的传递矩阵乘此矩阵，可得第2段终端参数：[X k2θk2M k2Q k2]=[−1.003−8.79e(−8)∗R A6.353−1.76e(−6)∗R A1.488e6−0.15∗R A7.241e6−1.023R A]用中间圆盘的传递矩阵乘第2段终端参数阵，即可得第3段起始端参数：[X03θ03M03 Q03]=[−1.003−8.79e(−8)∗R A6.353−1.76e(−6)∗R A1.85e6−0.249∗R A−8.556e6−2.408∗R A]用第3段传递矩阵乘其始端参数矩阵，得其终端参数：[X k3θk3M k3Q k3]=[−0.353−2.32e(−7)∗R A19.08−4.184e(−6)∗R A1.41e6−0.371∗R A−8.81e6−2.459∗R A]则，根据X k3=0可得：R A=−1.518e6;则，可得支座B后第4段的起始端参数阵为：[X04θ04M04 Q04]=[25.431.974e6−5.075e6−R B]同上，用此段轴的传递函数乘其起始端的状态参数，可得：[X k4θk4M k4 Q k4]=[0.898−7.03e(−10)∗R B34.33−7.03e(−8)∗R B1.822e6−3e(−2)∗R B−4.987e6−R B]则，根据M k4=0可得：R B=6.075e7;则，可得第5段的起始参数矩阵：[X05θ05M05 Q05]=[0.85530.055+θ5−6.574e7]其中，θ5为铰链处的转角。
转子动力学旋转机械的动力学特性
#6瓦
1000
1500
2000
2500
3000
机 组 转 速 r/m in
油膜轴承工作原理
最大油 膜间隙
收敛楔
o e o1 W
油膜压 力分布
发散楔
最小油 膜间隙
y 油膜失稳的机理
kxx cxx
油膜力
kyy cyy
fxkxxxkxyycxxxcxyy fykyxxkyyycyxxcyyy
o失
x
弹性力
多跨 轴 系 高压转子型 中压转子型 低压转子型 发电机转子型
刚性支承 2284
1643
2592 1142 3444
弹性支承 1936
1470
2014 1002 2678
轴系的各阶临界转速高于相应的单转子的临界转速。 弹性支承转子的临界转速低于刚性支承转子的临界转速。
转子的不平衡响应 unbalance response
转子与定子碰摩引起的失稳
转子与定子相碰时，有摩擦力Ft。 切向力Ft 推动转子绕 O 点作反向涡动 。
涡动频率 c/min
油膜涡动的波形和轴心轨迹
涡动频率约为转子转速的一半，并随转速变化。 涡动方向为正向进动。轴心轨迹出现双内环。 涡动的幅度并不很大。
油膜振荡的波形和轴心轨迹
到达阈速时突然发生，幅度一般很大。 涡动频率锁定在转子的固有频率，不再随转速变化。 涡动方向为正向进动。轴心轨迹为多重椭圆。 一旦发生不易消失，有惯性效应 。
转子运动的控制、非线性问题等。
临界转速 critical speed
临界转速是共振转速，转子在临界转速下会发生共振现象。 ▲ 临界转速在数值上一般等于转子横向振动的固有频率。 ▲ 临界转速的大小决定于转子的结构（质量和刚度的分布）和
转子动力学
题E-1: 两端弹性支撑薄单圆盘对称放置转子形心的瞬态涡动响应分析 已知：设有一弹性轴单盘转子如图1所示，弹性轴跨长ι=57cm,直径d =1.5cm,弹性模量62622.110kg/cm 20.5810N/cm E=⨯=⨯，材料密度337.810kg/cm ρ-=⨯。
两端的滚动轴承简化为弹性支座，支承刚度10/m x x k k A B ==N ，15/m y y k k A B ==N 。
圆盘厚2cm,∆=直径D=16cm,若不计重力影响与系统阻尼，圆盘的转动惯量近似按薄圆盘计算。
22=2 5.7rad /s 35.814rad /s ϕπ⨯= 。
求：①求解该转子形心稳态自由涡动时涡动频率与自转角速度的关系，画出涡动频率与自转角速度的关系曲线图。
② 若偏心距0.003mm e =,求出该转子稳态涡动响应。
③若轴承质量1kg b m =，求解该转子形心瞬态频率与自转角速度的关系。
图1.1解：（1）由题目给出的条件代入数据，得：()23160.57(),0.5()7.810 3.14159262 3.1372b d l m m kg m V kg ρρ-⎛⎫====A∆=⨯⨯⨯⨯= ⎪⎝⎭，，()22223.137160.0050192,20.010********d p d mD J kg m J J kg m ⨯===⋅==⋅（因为是动力对称转子圆盘）。
45334848 1.325610/,10/,15/64x y EI E d k N m k N m k N m l l π==⨯=⨯==。
对于两端支承刚度不对称动力对称转子的稳态自由涡动方程，即临界转速方程，如下：()()()()0000d b d b b b b x b b b b y b m x k x x m y k y y m x k x x k x m yk y y k y ⎧+-=⎪+-=⎪⎨--+=⎪⎪--+=⎩&&&&&&&& （1-1） 设方程的解为：cos sin cos sin b b b b x X t y Y t x X t y Y t=Ω⎧⎪=Ω⎪⎨=Ω⎪⎪=Ω⎩ （1-2） 代入稳态自由涡动方程式（1-1），得()()()()22220000d b d b x b b y b b k m x kx k m y ky kx k k m x ky k k m y ΩΩΩΩ⎧--=⎪⎪--=⎪⎨-++-=⎪⎪-++-=⎪⎩（1-3） 方程（1-3）是齐次方程。
电动机制造中的电机转子动力学分析考核试卷
四、判断题（本题共10小题，每题1分，共10分，正确的请在答题括号中画√，错误的画×）
1.电机转子在高速运转时，轴承的摩擦力对振动影响较小。（）
2.电机转子的临界转速越高，其工作转速范围就越宽。（）
3.转子的质量分布均匀时，不会产生不平衡。（）
B.滑动轴承
C.气浮轴承
D.磁浮轴承
14.在电机转子动力学分析中，以下哪些方法可以用来评估转子的稳定性？（）
A.线性稳定性分析
B.非线性稳定性分析
C.疲劳分析
D.振动分析
15.下列哪些措施可以减小电机转子在运输和安装过程中的损伤？（）
A.使用防震包装
B.严格控制安装工艺
C.增加转子材Leabharlann 的硬度D.避免在临界转速附近操作
A.材料密度不均匀
B.加工误差
C.装配不当
D.轴承磨损
9.下列哪些情况可能导致电机转子产生耦合振动？（）
A.转子与定子间的电磁力
B.转子与轴承间的相互作用
C.多级转子间的相互作用
D.外界环境的变化
10.在进行电机转子模态分析时，以下哪些参数是重要的？（）
A.转子的质量
B.转子的刚度
C.转子的阻尼
D.电机的工作温度
D.电机的温度
3.下列哪些方法可以改善电机转子的动力学特性？（）
A.调整轴承间隙
B.改善转子的质量分布
C.增加转子的质量
D.提高轴承的刚度
4.电机转子的一阶弯曲振动包括以下哪些部分？（）
A.轴向振动
B.弯曲振动
C.扭转振动
D.纵向振动
5.下列哪些因素会影响电机转子的临界转速？（）
汽轮机转子动力学分析与应用考核试卷
五、主观题（本题共4小题，每题10分，共40分）
1.请简述汽轮机转子临界转速的重要性，并说明影响临界转速的主要因素有哪些。
2.描述转子不平衡产生的原因及其对汽轮机运行的影响，并讨论如何通过振动分析识别转子不平衡。
3.详细解释油膜振荡的现象，包括其产生的原因、特征以及预防和控制措施。
5.用来描述转子系统稳定性的参数是______和______。（）
6.转子的裂纹可以通过______和______等方法进行检测。（）
7.为了减少转子启动和停机过程中的振动，应避免在临界转速______附近长时间停留。（）
8.转子的振动可以通过______和______等传感器进行监测。（）
9.汽轮机转子的热应力分析需要考虑的因素包括______和______。（）
2.转子不平衡由于质量分布不均造成，影响运行稳定性和轴承寿命ቤተ መጻሕፍቲ ባይዱ通过振动分析可识别不平衡，采取加重或去重校正。
3.油膜振荡是因油膜力与转子重量不平衡导致，特征为转速的一半。控制措施包括改善轴承设计和调整油膜厚度。
4.振动监测和故障诊断方法包括振动分析、温度监测和声发射技术，用于预测维护和故障排查，提高运行效率。
9.以下哪种方法通常用于转子不平衡的校正？()
A.加重法
B.去重法
C.调整轴承间隙
D. A和B
10.汽轮机转子在运行中，下列哪种情况可能导致转子径向振动？()
A.轴承故障
B.转子弯曲
C.叶轮损坏
D. A和B
11.在转子临界转速分析中，哪项因素与转子的一阶临界转速最相关？()
A.转子的长度
B.转子的直径
A.缓慢通过临界转速
转子动力学问题
绪论1、什么是Jeffcott转子，其研究意义是什么？2、转子动力学主要研究那些问题？3、转子动力学发展过程中的主要转折是什么？4、石化企业主要有哪些旋转机械，其基本工作原理是什么？第一章单盘转子的临界转速和不平衡响应1、什么是横向振动？2、什么是涡动（进动），其频率是多少？3、什么是自动对心？4、什么是临界转速？5、什么是刚性轴和柔性轴？6、什么是幅频响应曲线和相频响应曲线？7、什么是陀螺效应？产生陀螺力矩的基本条件是什么？8、怎样计算考虑陀螺力矩时转子的临界角速度？陀螺力矩对进动角速度数目和幅值的影响是什么？9、支撑刚度怎样影响转子的临界角速度？第三章滑动轴承的动力特性1、什么是收敛油楔、发散油楔？2、利用轴承的平衡半圆说明轴承的工作原理，并说明转速和载荷对轴承稳定性的影响。
3、什么是轴承的八个系数？对轴承的性能有何影响？4、什么是轴承的雷诺方程？其基本假设是什么？5、什么是紊流轴承理论？6、滚动轴承和滑动轴承的阻尼系数和刚度系数的取值范围是什么？7、什么是长轴承理论和短轴承理论？8、什么是浮环密封、静压轴承、阻尼轴承？第六章滑动轴承的油膜力与转子失稳1、什么是油膜力的分解及其对转子运动的影响？2、什么是油膜的半频涡动？3、什么是失稳角速度？4、什么是轴承的相似系数？5、转速如何影响轴径中心、园盘中心和涡动频率？6、油膜自激振动的特点是什么？第十章转子的平衡1、什么是静不平衡和动不平衡？2、什么是刚性转子和柔性转子？3、刚性转子平衡中，怎样进行离心惯性力系的等效简化？4、刚性转子的影响系数平衡方法是什么？5、柔性转子的影响系数平衡方法是什么？6、柔性转子的模态响应圆平衡方法是什么？。
python 转子动力学
python 转子动力学
Python转子动力学是一种利用Python编程语言实现的转子运动模拟方法。
它可以模拟转子在运转时的动态行为，包括转子的转速、振动、力学特性等。
该方法可以应用于各种领域，如机械制造、航空航天、能源等。
在机械制造领域，它可以用于转子设计和故障诊断；在航空航天领域，它可以用于模拟飞机发动机的运转情况；在能源领域，它可以用于模拟风力发电机的运转情况。
Python 转子动力学方法的优点在于其简单易懂、易于实现，同时还具有高效性、灵活性和可扩展性。
由于 Python 语言本身的特性，Python 转子动力学方法也可以与其他 Python 库结合使用，如 NumPy、SciPy 和 Matplotlib 等，以实现更加全面的数据处理和可视化。
- 1 -。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
转子动力学大作业
学院：
姓名：
班级：
学号：
目录
一、作业题目介绍
二、转子动力学理论简介
三、参数的选择和计算
四、Ansys分析临固有频率和临界转速
五、失稳转速影响因素及计算
一、大作业题目
1、 计算临界转速；
2、 圆轴承，长颈比为0.8，油膜间隙2‰
3、 计算失稳转速
注：转子两端各一个轴承，支点在左右两端。
二、转子动力学理论知识
由于制造中的误差，转子各微段的质心一般对回转轴线有微小偏离。
因此，当转子转动时，会出现横向干扰，在某些转速下还会引起系统强烈振动，出现这种情况时的转速就是临界转速。
为保证系统正常工作或避免系统因振动而损坏，转动系统的转子工作转速应尽可能避开临界转速，若无法避开，则应采取特殊防振措施。
这也是研究临界转速的意义。
临界转速和转子不旋转时横向振动的固有频率相同，也就是说，临界转速与转子的弹性和质量分布等因素有关，n k
m
ω=。
当圆盘不装在两支撑的中点而偏于一边时，转轴变形后，圆盘的转轴线与两支点A 和B 的连线有一夹角ψ。
设圆盘的自转角速度Ω，极转动惯量为p J ，则圆盘对质心o '的动量矩为 p H J =Ω。
它与轴线AB 的夹角也应该是ψ，见图1。
当转轴有自然振动时，设其频率为n ω，则圆盘中心o '与轴线AB 所构成的平面绕AB 轴有进动角速度n ω。
由于进动，圆盘的动量矩H 将不断改变方向。
因此有惯性力矩
()g n n p n M H H J ωωω=-⨯=⨯=Ω⨯
方向与平面o AB '垂直，大小为
sin g p n M J ωψ=Ω
1800mm
980mm 80
40
170
170
100 转子结构尺寸示意图
轮盘
轮盘
轮盘
这一惯性力矩称为陀螺力矩或回转力矩。
因夹角ψ较小，sin ψψ≈，上式可写作
g p n M J ωψ=Ω。
这一力矩与ψ成正比，相当于弹性力矩。
在正进动(0/2ψπ<<)的情况下，它使转轴的变形减小，因而提高了转轴的弹性刚度，即提高了转子的临界角速度。
在反进动（/2πψπ<<）的情况下，这力矩使转轴的变形增大，从而降低了转轴的弹性刚度，即降低了转子的临界角速度。
通过分析，可知道陀螺力矩对转子临界转速的影响：正进动时，它提高了临界转速；反进动时，它降低了临界转速。
图 1
在大多数情况下，轴承对于转子的动力特性有很明显的影响，轴承往往是阻尼的主要来源，因而控制着转子的响应。
同时，轴承的刚度和阻尼又影响着转子的临界转速和稳定性。
在深入研究转子动力学问题时，因而必须考虑到轴承的作用。
对于一个确定的轴承，当润滑油粘度及进油压已给定时，轴颈中心1o 的静平衡位置e 、ϕ决定于轴颈转速Ω和静载荷W 。
当载荷W 的大小或者轴颈转速Ω变化时，1o 位置也相应地变化。
当铅垂载荷W 大小变化时，
轴颈中心的移动在大多数情况下，并非沿铅垂方向，也即位移并不沿着载荷作用的方向。
这正是油膜不同于一般机械元件的一个特点。
记x F 、y F 为油膜力在x 、y 方向的分量。
我们定义油膜刚度系数为单位位移所引起的油膜力增量，即
x
xx F k x
∂=∂，0
y xy F k y
∂=
∂，0
y yx F k x
∂=
∂，0
y yy F k y
∂=
∂
定义油膜阻尼系数为单位速度所引起的油膜力增量，即
x xx F c x
∂=
∂，0
x xy F c y
∂=
∂，0
y yx F c x
∂=
∂，0
y yy F c y
∂=
∂
式中各系数的第一个下标代表力的方向，第二个下标代表位移或速度的方向。
油膜刚度系数和阻尼系数统称为油膜动力特性系数。
其中xy k ，yx k 和xy c ，yx c 分别称为交叉刚度系数和交叉阻尼系数，它们表示油膜力在两个相互垂直方向的耦合作用，交叉动力系数的大小和正
负在很大程度上影响着轴承工作的稳定性。
轴颈中心o '偏离轴承中心o 时，轴颈和轴承的间隙沿周向是不均匀的。
润滑油被轴颈带动，顺着转动方向从较宽的间隙流进较窄的间隙而形成油楔，对轴颈有挤压力作用。
当润滑油从较窄的间隙流到较宽的间隙时，因出现空穴而对轴有负压力。
轴承的全部油膜对轴颈的总压力F 位于挤压的一侧并朝向轴颈中心o '。
将F 力分解为o '点的径向力e F 和周向力F ψ。
分力e F 起支撑轴颈的作用，相当于转轴的弹性力。
分力F ψ垂直于o '的向径并顺着转动方向，是o '的速度增大，因而向径 oo '增大。
F ψ就是使轴颈运动失稳的力。
三、参数的选择与计算
初取0
52T C =，360/rad s Ω=，11
78000.01561060922
W Vg N ρ=
=⨯⨯⨯= /257.296(1/)N s π=Ω=,20.1D R m ==,0.80.08L D m ==,
40002210C D m -==⨯，选择粘度牌号为22号的润滑油，则214/mm s υ=。
动力粘度 632
1410900/ 1.2610kg m Pa s ηυρ--==⨯⨯=⨯
036301.88/()900/ 1.69210/()v c c kJ kg C kg m J m C ρ==⋅⨯=⨯⋅
22
2
41.261057.2960.10.080.05()()0.428609210
NDL R
S W C η--⨯⨯⨯⨯=
=⨯=⨯ 线性插值的油膜参数0.3120,0.8343, 6.4690Q P T ===
此时20=+0.8
()43018.016748.0167v R
Q
T T C c C P
ηπΩ=+=供油工作 020max =48.0167()48.0167 4.335652.3523v R
T T T C T C c C
ηΩ+∆=+
=+=工作
由于最高问题max T 跟假设的问题T 相近，故假设成立。
得轴承的动力特性系数：
1.9234,
2.6687, 6.0205, 1.6369xx xy yx yy k k k k ===-=
5.6411, 2.0471,11.8940xx xy yx yy c c c c ===-=
因为：,W W
k k
c c
C C ==Ω
66765.87510,8.12610, 1.810, 4.984410xx xy yx yy k k k k =⨯=⨯=-⨯=⨯ 4454.771410, 1.731510, 1.00610xx xy yx yy c c c c =⨯==-⨯=⨯ 四、Ansys 分析临固有频率和临界转速
1、 建立beam188和combination214单元，取
66765.87510,8.12610, 1.810, 4.984410xx xy yx yy k k k k =⨯=⨯=-⨯=⨯ 4454.771410, 1.731510, 1.00610xx xy yx yy c c
c c =⨯==-⨯=⨯
Campbell 图
若取刚度为87/xx
yy k k e N m ==，0/xy yx k k N m ==，13/xx yy c c e Ns m ==，
0/xy yx c c Ns m ==
可得Campbell 图
可见刚度系数对转子的固有频率及稳定性有着很大的影响。
用计算出的刚度系数，通过ANSYS计算得临界转速（r/min）
1 1831.943
2 1861.444
3 3451.431
4 3572.778
5 14317.884
6 15025.431
7 31665.300
8 33714.650
固有频率及模态振型：
一阶：
二阶：
三阶：
五、失稳转速影响因素及计算
转子运动失稳的原因除转轴的材料内阻或者圆盘与转轴配合面的摩擦以外，还有滑动轴承的油膜力。
因间隙不均匀而引起的横向气动力等等。
而对于大型汽轮机发电机组的转子或高速转子，轴承的油膜力引起转子运动失稳现象比较常见。
根据经验公式可以知道，失稳角速度: 11831.922=3663.886 43i c n n rpm ≈=⨯。