大学物理 第四版 第6章的1-3节
大学物理第6章第4节-驻波
x k (m), (k 0,1, 2, 3,4,5)
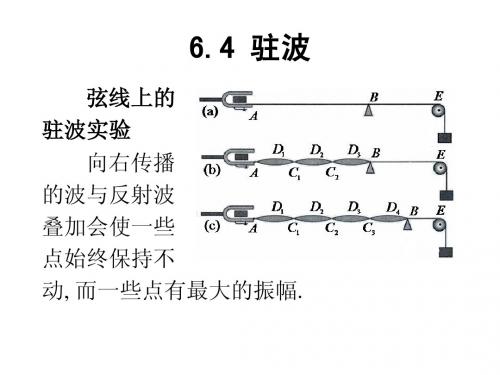
波腹位置
cos x 2 1
x
2 2 1 x k (m), (k 0,1, 2,3,4) 2
2k
, k 0,1, 2,
作业: (P. 152) 6.16 习题册: (P. 6) 1, (P. 7) 5
3 L O P 2 2
u
2
2
u
L
2
5
2
反射波沿x轴负向传播, 其波动方程
x y反 0.02 cos4 (t ) O 4 x 0.02 cos4 (t ) 4 2
在两个相邻波节之间的符号相同. (1) 波节两边的相位相反; (2) 两相邻波节之间的相位相同.
x
x
三. 半波损失 波在波密介质界面反射时, 反射波在界 形成波节 面处形成波节(发生 波疏介质 波密介质 的相位突变). 称为半 波疏介质 : u小 波损失. 波密介质 : u大 波在波疏介质界 波密介质 波疏介质 形成波腹 (自由端反射 ) 面反射 (称为自由端), 反射波在界面处形成波腹 (没有相位突变).
1 3 (m) x 100 2 k 2 3
t0
x
t T 6
x
t T 4
x
方法二
y1 0.06 cos[( 2)(8.0t 0.02x)] y2 0.06 cos[( 2)(8.0t 0.02x)]
相位差
( 2)(8.0t 0.02x) ( 2)(8.0t 0.02x)
1), ( 2 ) ( x 50(2k 2 3) (m)
第6章 机械波(大学物理赵近芳版)

G 切变模量
横波
E 弹性模量
纵波
K体积模量
343 m s 空气,常温
4000 m s 左右,混凝土
1.波长、波速、周期和频率这四个物理量中, 哪些量由传播介质决定?哪些量由波源决定?
答:波速由传播介质决定;周期和频率由波源 决定。
2.波速和介质质元的振动速度相同吗?它们各 表示什么意思?波的能量是以什么速度传播的?
2.横波与纵波 横波:质点振动方向与波的传播方向相垂直的波.
(仅在固体中传播 ) ➢ 特征:具有交替出现的波峰和波谷.
纵波:质点振动方向与波的传播方向互相平行的波.
(可在固体、液体和气体中传播) ➢ 特征:具有交替出现的密部和疏部.
u 波速 与介质的性质有关, 为介质的密度.
u
固体
u
液、气体u
u
λ
y(x,t) y(x,t T ) (波具有时间的周期性)
(2) 当t一定时,波函数表示该时刻波线上各点相对其平 衡位置的位移,即此刻的波形.
y(x,t) y(x ,t)(波具有空间的周期性)
波程差
x21 x2 x1
21
2
π
x21
(3) 若 x,t 均变化,波函数表示波形沿传播方
向的运动情况(行波).
dx
( dy )2 (w)2 A2 sin2[w(t x ) ]
dx
u
u
dWk
dWp
1 2
dVA2 2
sin 2 (t
x) u
6. 波动能量的传播 当机械波在媒质中传播时,媒质中各质点均在
其平衡位置附近振动,因而具有振动动能.
同时,介质发生弹性形变,因而具有弹性势能.
大一上物理课件 第六章

第六章 磁场通过复习后,应该:1.掌握磁感应强度、毕奥-萨伐尔定律、洛伦兹力、霍尔效应、安培力、磁场对载流线圈的作用、物质的磁性和磁化、电磁感应定律;2.理解几种电流的磁场、安培环路定理、质谱仪、超导体及其抗磁性、感生电动势、自感现象;3.了解磁场中的高斯定理、电磁流量计、超导磁体、人体生物磁场、涡旋电场。
6-1 一个半径为0.2m 、阻值为200Ω的圆形电流回路,接12V 的电压,求回路中心处的磁感应强度。
解: 已知半径r =0.2m ,电源电压U =12V ,圆形回路的电阻R =200Ω,根据欧姆定律,可求得回路的电流为I =U / R =12/200 A=0.06 A由圆形电流磁场公式,可得回路中心处的磁感应强度为T 10881T 2020601042770--⨯=⨯⨯⨯==...r IB πμ6-2 一根长直导线上载有电流100A ,把它放在50G 的均匀外磁场之中,并使导线与外磁场正交,试确定合成磁场为零的点到导线的距离。
解: 长直载流导线产生的磁场,其磁感线是一些围绕导线的同心圆,在导线周围总有一点A ,其磁感强度与外磁场的磁感应强度大小相等、方向相反,该点的合磁场为零。
已知I =100A ,B = 50G = 5.0×10-3 T ,根据长直载流导线磁场公式aI B πμ20=,可得A 点离导线的距离a 为mm 04m 1004m 1005210010423370...B I a =⨯=⨯⨯⨯⨯==---πππμ6-3 0.4m 长的细管上绕有100匝导线,其电阻为3.14Ω,欲在螺线管内获得200G 的磁感应强度,需外加电压多少伏?解: 已知螺线管单位长度上的线圈匝数n =100/0.4=250匝·米-1,B =200G =2×10-2 T ,根据螺线管电流磁场公式B = μ0nI ,可得螺线管通过的电流为A 763A 102A 2501041022720.nB I ≈⨯=⨯⨯⨯==--ππμ 已知线圈电阻R =3.14Ω,根据欧姆定律可计算出需加的外电压为U =IR =2/π×102×3.14V=200V6-4 一平面上有两个同心的圆形回路,用相同电动势的电池(内阻忽略不计),通过相反方向的电流,使在中心处产生的磁感应强度为零,已知外圆用铜线,其电阻率为1.7×10-6Ω·cm ,内圆用铝线,电阻率为2.8×10-6Ω·cm ,这些导线的截面积相同,外圆直径为200cm ,求内圆的直径。
大学物理学:第六章 大气热力学基础

2)物理意义: 在等压过程中,系统焓的增量值等于它所吸收的热量。
3)定压比热Cp
Cp
( Q) p
dT
H T
p
热容量和焓
• 热量是在过程中传递的一种能量,是与过程有关的。一个系统在 某一过程中温度升高1K所吸收热量,称作系统在该过程的热容量。
• 对于等容过程,外界对系统不做功,Q =ΔU,所以
s T
p
1 T
h T
p
cp T
(26)
s
p
T
T
p
ds
s T
p
dT
s p
T
dp
(6.1.22)
ds
cp T
dT
T
P
dp
cpd
ln T
pdp
(6.1.28)
以6.1.25和6.1.27代入6.1.23式
dh
h T
p
dT
h p
T
dp
(6.1.23)
dp
cpdT
Hale Waihona Puke 1dp四、热力学第二定律
能量守恒,反映物质运动不灭但是没有回答过程的方向性(可 逆与不可逆)。
热力学第二定律的实质
指出了自然界中一切与热现象有关的实际过程都是不可逆过程, 揭示出实际宏观过程进行的条件和方向。
自然过程的方向性
• Example 1 功热转换过程的方向性 • 功变热的过程是不可逆的。 • 卡诺循环:吸收热量Q1,做功,必须有一部分热量
dG SdT Vdp (6.1.20)
dG
G T
p
dT
G p
T
dp
G T
p
S,
G
大学物理第六章

则系统吸收热量是
Q M m C K (T 2T 1)
(6 .6)
(1)注意c、CK两者的差别;
(2)经历过程不同时,Ck不同,吸收(放出) 热量 也不同,所以Q是过程量。
(3)系统吸热或放热,会使系统状态变化,即内能
发生变化。
传热微 分子无规则运动的能量 碰撞
观本质 从高温物体向低温物体的传递。
当热力学系统的状态随时间变化时,我们称 系统经历了一个热力学过程。
二、准静态过程
过程的中间状态都无限接近于平衡态,这样的过 程可以用系统的一组状态参量的变化来描述,这样的 过程称为准静态过程(quasi-static process)。
是一种理想的热力学过程,优点在于对过程变化的
描述和讨论都比较方便和简捷,并可进行数学处理。实
A PV=C
绝热Q=0
AE
m M
CV
T
E
0
PV C
特点1) ET, ~状态量。
2) A V2 PdV V1
~过程量。 C
C
P
V
C
i 2
V
R
R
3) 2019/11/22
m QMCKT
吉林大学
过
物理教学中心
程
量C C
T
Q
0
【例3】
P
P'2 P2
绝热过程中的功:
O
I A II
V1
V2 V
由热力学第一定律
d A P d V d E M mCVdT
AEM mCV(T2-T1)
绝热方程(Adiabatic Equation)
将理想气体状态方程 PV m RT 全微分,
工程力学第四版第六章ppt

上一页 下一页
返回
三、质点运动微分方程 及其应用
返回首页
设质量为m的质点M,在合力F的作用下,以加
速度a运动,如图所示。根据动力学基本方程有
ma=F
(6-1)
它在直角坐标系的投影方程为
m
d2x dt 2
Fx
d2 y m dt 2 Fy
m
d2z dt 2
Fz
(6-4)
上一页 下一页
返回
工程中,有时采用动力学基本方程在自然坐 标系上的投影较为方便。在点作平面曲线运动时, 它在自然坐标系的质点运动的微分方程为
可见,质点的运动轨迹是以a、b为半轴的椭圆。对 运动方程求二阶导数,即
将上式代入式(6-4),得F在坐标轴上的投影
可见,力F和点M的位置矢径r方位相同、指向相 反,F始终指向中心,其大小与r的大小成正比,称之 为有心力。
2)质点动力学第二类问题———已知作用于质点上 的力,求质点的运动。
例6 - 4 液压减振器工作时,活塞在液压缸内作直线 运动。若液体对活塞的阻力正比于活塞的速度v,即F R =μv,其中μ为比例常数。设初始速度为v0,试求 活塞相对于液压缸的运动规律,并确定液压缸的长度。
故
例6-2 卷扬小车连同 起吊重物一起沿横梁以匀速 v0向右运动。此时,钢索 中的拉力等于重力G。当卷 扬小车突然制动时,重物将 向右摆动,如图所示。求此 时钢索中的拉力,设钢索长 为l。
解 取自然坐标系如图所示。重物在摆动过程中,其上作用有重 力、钢索拉力。应用自然坐标形式的质点运动微分方程式(6-5), 得
上一页 返回首页 下一页
第一节 质点动力学基本方程
返回首页
一、质点动力学基本方程
由经验可知,要改变一个物体的运动状态(即 产生加速度),都必须对物体施加力。用同样大的 力来推质量不同的物体,则质量大的物体产生的加 速度小,质量小的物体产生的加速度就大。它们的 这样关系可用牛顿第二定律阐述如下:质点受力作 用时所获得加速度的大小,与作用力的大小成正比, 与质点的质量成反比,加速度的方向与力的方向相 同。
大学物理第6章习题参考答案
第六章习题解答6-1 解:首先写出S 点的振动方程 若选向上为正方向,则有:0c o s02.001.0ϕ=- 21cos 0-=ϕ,0s i n 00>-=ϕωυA 0sin 0<ϕ 即 πϕ320-=或π34 初始相位 πϕ320-=则 m t y s )32cos(02.0πω-=再建立如图题6-1(a)所示坐标系,坐标原点选在S 点,沿x 轴正向取任一P 点,该点振动位相将落后于S 点,滞后时间为: ux t =∆则该波的波动方程为:m u x t y ⎥⎦⎤⎢⎣⎡--=πω32)(cos 02.0若坐标原点不选在S 点,如习题6-1图(b )所示,P 点仍选在S 点右方,则P 点振动落后于S 点的时间为: uL x t -=∆则该波的波方程为:m uL x t y ⎥⎦⎤⎢⎣⎡---=πω32)(cos 02.0若P 点选在S 点左侧,P 点比S 点超前时间为ux L -,如习题6-1图(c)所示,则⎥⎦⎤⎢⎣⎡--+=πω32)(cos 02.0u x L t y⎥⎦⎤⎢⎣⎡---=πω32)(cos 02.0uL x t∴不管P 点在S 点左边还是右边,波动方程为: ⎥⎦⎤⎢⎣⎡---=πω32)(cos 02.0uL x t y6-2 解(1)由习题6-2图可知, 波长 m 8.0=λ 振幅A=0.5m习题6-1图习题6-1图频率 Hz 125Hz 8.0100===λuv周期 s 10813-⨯==vT ππυω2502==(2)平面简谐波标准波动方程为: ⎥⎦⎤⎢⎣⎡+-=ϕω)(cos u xt A y 由图可知,当t=0,x=0时,y=A=0.5m ,故0=ϕ。
将ϕπωω、、、u v A )2(=代入波动方程,得:m )100(250cos 5.0⎥⎦⎤⎢⎣⎡-=x t y π(3) x =0.4m 处质点振动方程.⎥⎦⎤⎢⎣⎡-=)1004.0(250cos 5.0t y π m )250cos(5.0ππ-=t6-3 解(1)由习题6-3图可知,对于O 点,t=0时,y=0,故2πϕ±=再由该列波的传播方向可知,00<υ取 2πϕ=由习题6-3图可知,,40.0m OP ==λ且u=0.08m/s ,则ππλππω52rad/s 40.008.0222====u v rad/s可得O 点振动表达式为:m t y )252cos(04.00ππ+=(2) 已知该波沿x 轴正方向传播,u=0.08m/s,以及O 点振动表达式,波动方程为:m x t y ⎥⎦⎤⎢⎣⎡+-=2)08.0(52cos 04.0ππ(3) 将40.0==λx 代入上式,即为P 点振动方程:m t y y p ⎥⎦⎤⎢⎣⎡+==ππ2152cos 04.00 (4)习题6-3图中虚线为下一时刻波形,由图可知,a 点向下运动,b 点向上运动。
大学物理第6章-3.ppt
C 2e
2 ( 2 0 )t
其中C1,C 2 是积分 常数,由初始条件 来决定,这种情况 称为过阻尼。
无振动发生。
x( t )
t
过阻尼
(3) 如果
0 方程的解:
t
x( t )
x(t ) (C1 C2 t )e
C1 , C 2 是由初始条件
t
临界阻尼
欠阻尼振动的特点:
振幅随时间 t 作指数衰减。 近似为简谐振动。 阻尼振动周期比系统的固有周期长。
x
A0 e t cos(t )
A0 e t
o
t
(2) 0 阻尼较大时(过阻尼), 方程的解:
x ( t ) C 1e
2 ( 2 0 )t
第六章 振动学基础 阻尼振动
阻尼振动
阻尼振动
振幅随时间而减小的振动叫做阻尼振动。 1、阻尼的分类 a、摩擦阻尼:机械能转化为热能。 b、辐射阻尼:能量辐射出去,形成波(音叉、乐器等)。 x 2、阻尼振动的动力学方程 k m F m fr x 实验表明当速度不太大时: o p dx 为阻力系数。 粘滞阻力: f r v dt 2 d x dx 动力学方程: m kx 2 dt dt k 2 令 0 m 2m
x
欠阻尼 临界阻尼
决定的积分常数。
称之为临界阻尼情 况。它是振动系统刚刚不能作 准周期振动,而很快回到平Βιβλιοθήκη o 位置的情况,应用在天平调衡 中。
0
过阻尼
t
d2 x dx 2 2 0 x 0 2 dt dt
固有角频率 0
阻尼因子
k m 由系统本身的性质决定。 2m 由阻力系数决定。
大学物理学第四版第一到六章课后题答案
习题11.1选择题(1) 一运动质点在某瞬时位于矢径),(y x r的端点处,其速度大小为(A)dtdr (B)dt r d(C)dtr d ||(D)22)()(dtdy dt dx + [答案:D](2) 一质点作直线运动,某时刻的瞬时速度s m v /2=,瞬时加速度2/2s m a -=,则一秒钟后质点的速度(A)等于零 (B)等于-2m/s (C)等于2m/s (D)不能确定。
[答案:D](3) 一质点沿半径为R 的圆周作匀速率运动,每t 秒转一圈,在2t 时间间隔中,其平均速度大小和平均速率大小分别为 (A)tR t R ππ2,2 (B) t Rπ2,0 (C) 0,0 (D)0,2tR π [答案:B] 1.2填空题(1) 一质点,以1-⋅s m π的匀速率作半径为5m 的圆周运动,则该质点在5s 内,位移的大小是 ;经过的路程是 。
[答案: 10m ; 5πm](2) 一质点沿x 方向运动,其加速度随时间的变化关系为a=3+2t (SI),如果初始时刻质点的速度v 0为5m·s -1,则当t 为3s 时,质点的速度v= 。
[答案: 23m·s -1 ](3) 轮船在水上以相对于水的速度1V 航行,水流速度为2V ,一人相对于甲板以速度3V行走。
如人相对于岸静止,则1V 、2V和3V 的关系是 。
[答案: 0321=++V V V]1.3 一个物体能否被看作质点,你认为主要由以下三个因素中哪个因素决定:(1) 物体的大小和形状; (2) 物体的内部结构; (3) 所研究问题的性质。
解:只有当物体的尺寸远小于其运动范围时才可忽略其大小的影响,因此主要由所研究问题的性质决定。
1.4 下面几个质点运动学方程,哪个是匀变速直线运动?(1)x=4t-3;(2)x=-4t 3+3t 2+6;(3)x=-2t 2+8t+4;(4)x=2/t 2-4/t 。
给出这个匀变速直线运动在t=3s 时的速度和加速度,并说明该时刻运动是加速的还是减速的。
大学物理2-1第六章(振动与波)习题答案
精品习 题 六6-1 一轻弹簧在60N 的拉力下伸长30cm 。
现把质量为4kg 物体悬挂在该弹簧的下端,并使之静止,再把物体向下拉10cm ,然后释放并开始计时。
求:(1)物体的振动方程;(2)物体在平衡位置上方5cm 时弹簧对物体的拉力;(3)物体从第一次越过平衡位置时刻起,到它运动到上方5cm 处所需要的最短时间。
[解] (1)取平衡位置为坐标原点,竖直向下为正方向,建立坐标系rad/s 07.74200m 1.0N/m 2001030602=====⨯=-m k A k ω设振动方程为 ()φ+=t x 07.7cos0=t 时 1.0=x φcos 1.01.0= 0=φ故振动方程为 ()m 07.7cos 1.0t x =(2)设此时弹簧对物体作用力为F ,则()()x x k x k F +=∆=0其中 m 2.0200400===k mg x精品因而有 ()N 3005.02.0200=-⨯=F(3)设第一次越过平衡位置时刻为1t ,则()107.7cos 1.00t = 07.5.01π=t第一次运动到上方5cm 处时刻为2t ,则()207.7cos 1.005.0t =- ()07.7322⨯=πt故所需最短时间为:s 074.012=-=∆t t t6-2 一质点在x 轴上作谐振动,选取该质点向右运动通过点 A 时作为计时起点(t =0),经过2s 后质点第一次经过点B ,再经 2s 后,质点第二经过点B ,若已知该质点在A 、B 两点具有相同的速率,且AB =10cm ,求:(1)质点的振动方程:(1)质点在A 点处的速率。
[解] 由旋转矢量图和||||b a v v =可知421=T s精品由于4/2s 8/1,s 81ππνων====-T精品(1) 以AB 的中点为坐标原点,x 轴指向右方。
t =0时, φcos 5A x =-=t =2s 时, φφωsin )2cos(5A A x -=+==由以上二式得 1tan =φ因为在A 点质点的速度大于零,所以43πφ-= cm x A 25cos /==φ所以,运动方程为:)SI ()4/34/cos(10252ππ-⨯=-t x(2)速度为: )434sin(41025d d 2πππ-⨯-==-t t x v 当t =2s 时 m/s 1093.3)434sin(41025d d 22--⨯=-⨯-==πππt t x v6-3 一质量为M 的物体在光滑水平面上作谐振动,振幅为 12cm ,在距平衡位置6cm 处,速度为24s cm ,求:(1)周期T ; (2)速度为12s cm 时的位移。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
- - - ' - r d E0 E ' E
+ + +
0 +++++++++++
0 E0 0
设极化电荷面密度 '
-----------
+ + +
E
0
- - - - - r d E0 E ' E
+ + +
+++++++++++
E E0 E
解:放入电介质前, 两板间的电场强度为:
U E0 10 3 KV .m 1 d
+ + + + + + + + +
0
d r E0 E' E
+ + +
- - - ' -
+ +
---------
放入电介质后,两板间的 E0 E 3.33102 KV .m 1 电场强度为: r
R2
R1
解 (1) 求电介质中的电场强度、电位移和极化 强度;
r
R2
R1
L
作一与圆柱导体同轴的长为L的柱形高斯面
由于电场具有轴对称性, 因此高斯面上的电位移 矢量大小处处相等. 由介质中的高斯定理得,
D dS Q0 L
S
D 2 π rL L
/19
D 2 π rL L
0 R3 R2 R1
q 1 2q V0 0 dr 0 dr R3 4 r 2 R1 4 r 2 将E代入后得到: 0 0 q 1 1 2 ( ) 4 0 R3 R2 R1 R2
1
电场线
6 -2
34推广
电介质
实验测得两板间的电场 强度E的值仅为 真空时两板间电场强度 的 1 倍, 即 E
(1)各向同性介质; (2)自由电荷和介质的分布具有对称性(均匀无 限大电介质充满全场,或介质分界面为等势面)。
把一块相对电容率 r 3的电介质, 放在板间距 d 1m m的两平行 带电平板之间 放入之前, 两板的电势差是1000 , 若放入电介质后两平 , V 板上的电荷面密度保持 不变, 试求两板间电介质内的 电场强度 E ,电极 化强度 P, 平板和电介质的电荷面 密度,电介质内的电位移D
如何分布?球心电势为多少?
q
q
R3
S3
R3 3
q
R2
q
2q
r
R1 1
R2
R1
解:+q 分布在内球壳外表面,静电感应后, 外球壳内表面带 - q,外表面将带电量 q+q
解: 为了计算球心的电势,必须先计算出各点的电场
强度。
作球形高斯面 S1
E1 0 (r R3 )
R1 q
S2
R3
1 R
对于有尖端的带电导体,尖端处电荷 •
面密度大,则导体表面邻近处场强也 特别大。当场强超过空气的击穿场强 时,就会产生空气被电离的放电现象, 称为尖端放电。
σE
避雷针的工作原理 + + •电晕现象 (高压输电线周围的水滴由于重力和电 + + +
作球形高斯面 S2 q S2 E2 dS ε0
q E2 ( R3 r R2 ) 2 4 π ε0 r
q
S1
R2
R1
r
作球形高斯面 S3
S3
E3 dS 0
S4
R1
S3
R3 3
E3 0 ( R1 r R2 )
作球形高斯面 S 4 2q S E4 dS ε0
0
r
E0 0
E
E0
r
r 叫做电介质的电容率
0 叫做真空电容率
r 0
叫做电容率
电介质
电介质
H H H
1040
C
H
甲烷 CH 4
O
H 2O
正负中心不重合相 当于一个电偶极子
位移极化
转向极化
• 不同电介质极化的微观机理不尽相同,但 是在宏观上,都表现为在电介质表面出现
电介质中的电位移为:
D r 0 E 0 E0 8.85106 C m2
图中是由半径为R1的长直 圆柱导体和同轴的半径为R2的 薄导体圆筒组成,其间充以相 对电容率为r的电介质. 设直导 体和圆筒单位长度上的电荷分 别为+和- . 求(1)电介质中 的电场强度、电位移和极化强 度; (2)电介质内外表面的极 化电荷面密度.
( R1 r R2 )
电场强度、电位移和极化强度的方向都是垂直直导体并沿径向方向指向外. /19
(2) 求电介质内、外表面的极化电荷面密度; r R1 R
2
因为
r 1 P ( r 1) 0 E 2π r r
r 1 P 1 2 π r R1 r 1 P 2 2 π r R2
电介质中的 与E呈线性关系 P
作业
作 业
6- 8 6 - 13
6- 9
电场线
6 -3
介质高斯定理
电位移矢量D
介质高斯定理
S
D dS
q
0 S内
通过电介质中任一封闭曲面 S 的电位移通 量等于该曲面所包围的自由电荷的代数 和。 ——介质中的高斯定理
介质中高斯定理的应用条件:
极化电荷。
• 极化电荷与自由电荷不同 不能通过传导或
接地方法离开电介质。
• 附加电场
极化电荷产生的附加电场将 影响和削弱原电场
(仅讨论各向同性的均匀介质)
用单位体积内分子电偶极矩的矢量和来定 量描述该处电介质的极化程度。它是量度电介 质内某点极化状态的物理量。 p P V
小写 p :分子电偶极矩;
带电云 场力的共同作用下,使带电水滴的尖端附近的场特别大, -- - - - - 从面使大气中的气体分子电离,而形成放电现象。) +
+
尖端放电现象的利与弊
静电感应 弊: 尖端放电会损耗电能, 还会干扰精密测量和对通 电晕放电 讯产生危害 . 因此,高压电器设备中要避免带有尖棱. 可靠接地
利: 尖端放电也有很广泛的应用 . 例如,
避雷针 -- 尖端放电现象的利用, 有目的地将大气中的大量电 避雷针 -- 尖端放电现象的利用, 有目的地将大气中的大量电荷通过避雷 荷通过避雷针的尖端引向大地.
针的尖端引向大地.
静电屏蔽
例 有一外半径R1=10 cm,内半径R2=7 cm 的金属 球壳,在球壳中放一半径R3=5 cm的同心金属球,若使 球壳和球均带有q=10-8 C的正电荷,问两球体上的电荷
基本定理的特殊应用
电荷重新分布 影响 原有电场
静电平衡状态
电场重新分布
Contents 静电场中的导体 静电场的电介质
Chapter 6
电位移、有电介质时的高斯定理 电容、电容器
静电场的能量、能量密度
6-0
教学基本要求
一 掌握静电平衡的条件,掌握导体 处于静电平衡时的电荷、电势、电场分布. 二 了解电介质的极化机理,掌握电 位移矢量和电场强度的关系.理解电介质中 的高斯定理,并会用它来计算电介质中对 称电场的电场强度.
6-0
教学基本要求
三 掌握电容器的电容,能计算常见 电容器的电容.
四 理解电场能量密度的概念,掌握 电场能量的计算.
6 -1
导体静电平衡
导体达到静电平衡条件是:
静电平衡条件
证明: 表 导体表面 E
1
若E表 表面,E 0,自由
电子沿表面有宏观运动,则未达静 电平衡状态。与静电平 衡条件矛盾, 故有E表 表面。
大写 P :电极化强度
(1)电极化强度矢量
单位(SI):
库仑 米2 C m2
极化强度与极化电荷的关系
上。在电介质内取一个长度为l、底面积为S的圆柱体.
若把整个圆柱体看为一个“大 S 电偶极子”,它的电矩的大小为 Sl,所以,圆柱体内分子电 0 + + + + + + + + + + + 矩的矢量和的大小可以表示为
4
q
R2
q q
2q
r
R1
R1 1 1 1
2q E4 (r R1 ) 2 4 π ε0 r
S3
R3
q
R2
q
2q
0 q
0 r R3
2
r
R1
E
4 0 r 0
R3 r R2 R2 r R1 r R1
2q 4 0 r 2
V0 E dl 0 由电势的定义可得 R2 R1 R3 球心处的电势为: E1 dl E2 dl E3 dl E4 dl
导体与电介质
电场线
根据物体的导电性可将物体分成三类:
• 导体 导电性能很好的材料
(各种金属、电解质溶液)
• 电介质(绝缘体 ) 导电性能很差的材料
(云母、胶木等)
• 半导体
