湘教版八年级正方形复习
八年级数学下册第2章四边形2.7正方形教学课件新版湘教版

D
O C
【例题】
例2:AC为正方形ABCD的对角线,E为AC上一点,且AB=AE,EF⊥AC交BC 于F,求证形
3.(宜宾·中考)如图,点P是正方形ABCD的对角线
BD上一点,PE⊥BC于点E,PF⊥CD于点F,连接EF,给出
下列五个结论:①AP=EF;②AP⊥EF;③△APD一定是等
腰三角形;④∠PFE=∠BAP;⑤PD= EC.其中正确结
2
论的序号是_____.
【解析】延长FP交AB于点G,延长AP交EF于点H,交EC于 点M,由题意易证,△BPE、△DPF为等腰直角三角形,四边 形PECF为矩形,四边形BEPG为正方形. 易证△APG≌△FEP, 所以AP=EF,∠BAP=∠PFE,又PE∥FC, 所以∠PFE=∠FEC=∠BAP, 又∠BAP+∠BMA=90°,所以∠FEM+∠BMA=90°, 所以∠EHM=90°即AP⊥EF. 在等腰直角三角形PDF中, PD= 2 PF= 2EC. 答案:①②④⑤
平行四边形
矩形
正 菱形 方
形
1.(义乌·中考)下列说法不正确的是( ) (A)一组邻边相等的矩形是正方形 (B)对角线相等的菱形是正方形 (C)对角线互相垂直的矩形是正方形 (D)有一个角是直角的平行四边形是正方形 【解析】选D.有一个角是直角的平行四边形可能是矩形, 也可能是正方形.
2.(苏州·中考)如图,四边形 ABCD是正方形,延长AB到E,使AE=AC, 则∠BCE的度数是_______°. 【解析】因为四边形ABCD是正方形, 所以∠CAE=45°,∠ABC=90°, 又因为AE=AC,所以∠E=∠ACE=67.5°, 所以∠BCE=90°-∠E=90°-67.5°=22.5°. 答案:22.5
湘教版初中数学八年级下册2.7 正方形

TB:小初高题库
湘教版初中数学
知识点 2 正方形的判定 6.下列说法不正确的是( )
9.如图,四边形 ABCD 中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD 于点 E,且四边形 ABCD 的面积为 8,则 BE 等于( )
A.2
B.3
C.2 2
D.2 3
第 9 题图
第 10 题图
10.如图,将 n 个边长都为 2 的正方形按照如图所示摆放,点 A1,A2,…,An 分别是正方形的
PE+PC 的最小值是__________.
14.如图,在正方形 ABCD 中,点 M 是对角线 BD 上的一点,过点 M 作 ME∥CD 交 BC 于
点 E,作 MF∥BC 交 CD 于点 F.求证 AM=EF.
15.如图,四边形 ABCD 是正方形,BE⊥BF,BE=BF,EF 与 BC 交于点 G. (1)求证:AE=CF; (2)若∠ABE=55°,求∠EGC 的大小.
中心,则这 n 个正方形重叠部分的面积之和是( )
1
1
A.n
B.n-1
C.( )n-1
D. n
4
4
11.已知四边形 ABCD 是平行四边形,再从①AB=BC,②∠ABC=90°,③AC=BD,④AC
⊥BD 四个条件中,选两个作为补充条件后,使得四边形 ABCD 是正方形,现有下列四种
选法,其中错误的是( )
A.一组邻边相等的矩形是正方形 B.对角线相等的菱形是正方形 C.对角线互相垂直的矩形是正方形 D.有一个角是直角的平行四边形是正方形 7.在四边形 ABCD 中,O 是对角线的交点,能判定这个四边形是正方形的条件是() A.AC=BD,AB∥CD,AB=CD B.AD∥BC,∠A=∠C C.AO=BO=CO=DO,AC⊥BD D.AO=CO,BO=DO,AB=BC 8.如图正方形 ABCD 中,E,F 分别为 BC,CD 上的点,且 AE⊥BF,垂足为 G,求证: AE=BF.
2024八年级数学下册第2章四边形2.7正方形2.7.1正方形的性质习题课件新版湘教版

边在正方形ABCD外作正方形CEFG,连接BG,DE.
(1)猜想图①中线段BG、线段DE的长度关系及所在直线的
位置关系,并说明理由;
【解】BG=DE,BG⊥DE.理由如下:
如图①,∵四边形ABCD和四边形CEFG都是正方形,
∴BC=DC,∠BCG=∠DCE=90°,CG=CE,
∴△BCG≌△DCE,∴BG=DE,∠1=∠2.
延长BG交DE于点H.
∵∠1+∠CGB=90°,∠1=∠2,∠CGB=∠DGH,
∴∠2+∠DGH=90°,∴∠DHG=90°.
∴BH⊥DE,即BG⊥DE.
(2)将图①中的正方形CEFG绕着点C按顺时针(或逆时针)
方向旋转任意角度α,得到如图②③的情形.请你通过观
(第2题)
3. [2023·重庆A卷 新考法·旋转法]如图,在正方形ABCD中,
点E,F分别在BC,CD上,连接AE,AF,EF,∠EAF=
45°,若∠BAE=α,则∠FEC一定等于( A )
A.2α
B.90°-2α
C.45°-α
D.90°-α
(第3题)
【点拨】
在正方形ABCD中,AD=AB,∠BAD=∠ABC=∠ADC=
(1)求证:∠DAG=∠EGH;
【证明】在正方形ABCD中,AD⊥CD,
∵GE⊥CD,∴AD∥GE,
∴∠DAG=∠EGH.
(2)判断AH与EF是否垂直,并说明理由.
【解】AH⊥EF,理由如下.
连接GC交EF于点O,如图.
∵BD为正方形ABCD的对角线,
∴∠ADG=∠CDG=45°.
又∵DG=DG,AD=CD,
得∠BEO=∠AFO=70°,从而可求出∠CBE的度数.
2021年湘教版八年级数学下册第二章《正方形》精品课件 (2)

∴ ∠GEF = 900. ∴ 四边形EFGH是正方形.
巩固练习
1. 正方形具有而菱形不一定具有的性质是( C )
(A)四条边相等 (B)对角线互相垂直且平分
(C)对角线相等 (D)对角线平分一组对角
2. 正方形具有而矩形不一定具有的性质是( B )
(A)四个角相等 (B)对角线互相垂直且平分
(C)对角线相等 (D)对角互补
• 14、Thank you very much for taking me with you on that splendid outing to London. It was the first time that I had seen the Tower or any of the other famous sights. If I'd gone alone, I couldn't have seen nearly as much, because I wouldn't have known my way about.
10、人的志向通常和他们的能力成正比例。2021/2/62021/2/62021/2/62/6/2021 5:22:24 AM 11、夫学须志也,才须学也,非学无以广才,非志无以成学。2021/2/62021/2/62021/2/6Feb-216-Feb-21 12、越是无能的人,越喜欢挑剔别人的错儿。2021/2/62021/2/62021/2/6Saturday, February 06, 2021 13、志不立,天下无可成之事。2021/2/62021/2/62021/2/62021/2/62/6/2021
又 AE = BF = CG = DH, F ∴ HA = FB = CF = DG.
3.4正方形 教案(湘教版八年级下)
探究内容: 3.4 正方形目标设计:1、理解并掌握正方形的有关性质与判定方法,能利用其相关知识进行推理与证明;2、能准确画出一个正方形;3、培养学生自主探究知识的能力。
重点难点:运用正方形的性质定理和判定定理进行推理与计算。
探究准备:投影片、作图工具等。
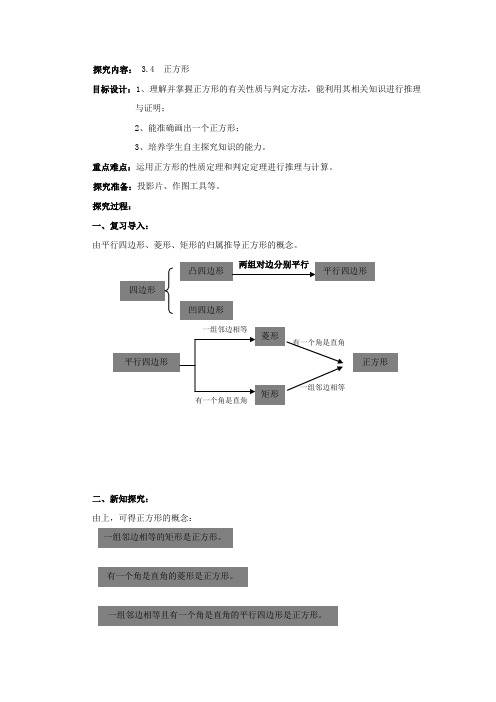
探究过程:一、复习导入:由平行四边形、菱形、矩形的归属推导正方形的概念。
二、新知探究:由上,可得正方形的概念:凸四边形 凹四边形 平行四边形 两组对边分别平行 正方形 一组邻边相等的矩形是正方形。
有一个角是直角的菱形是正方形。
一组邻边相等且有一个角是直角的平行四边形是正方形。
推测:1、正方形既是菱形,又是矩形,其性质有:①四边相等,四个角都是直角;②对角线相等且互相垂直平分,每条对角线平分一组对角;③是中心对称图形,也是轴对称图形。
2、正方形的判定方法:正方形定义的几种不同说法都是判定方法。
思考:如图,正方形ABCD被它的两条对角线AC、BD分成了四个三角形,它是什么样的特殊三角形?它们全等吗?分析:方法一:正方形的对角线相等且互相平分;方法二:正方形的两条对角线所在的直线都是它的对称轴;方法三:直角三角形斜边上的中线等于斜边的一半;方法四:正方形是中心对称图形。
探究正方形的画法:1、已知边长画正方形:先画直角再截取长度,后平移线段2、已知对角线画正方形:先画两条互相垂直平分且相等的线段,再顺次连结线段的端点即可。
三、练习:P104练习题1、2、3四、小结:1、正方形的概念,即正方形的判定方法:①一组邻边相等的矩形是正方形;②有一个角是直角的菱形是正方形;③一组邻边相等且有一个角是直角的平行四边形是正方形。
2、正方形的性质,综合了菱形和矩形的所有性质。
3、正方形的画法:①已知边长;②已知对角线。
五、作业:1、课堂:P105习题3.4B组1;2、课外:P104习题3.4A组;B组2.。
湘教版八年级数学下册2.7 正方形2

2.7 正方形【知识与技能】1.能说出正方形的定义和性质.2.会运用正方形的概念和性质进行有关的论证和计算.【过程与方法】1.经历探究正方形性质的过程,进一步发展学生的合理论证能力.2.通过由一般到特殊的研究方法,分析平行四边形、矩形、菱形、正方形的概念及性质之间的区别与联系.3.探索并掌握正方形的性质.【情感态度】1.在探究正方形性质的过程中,发现正方形的结构美和应用美,激发学生学习数学的热情.2.进一步加深对“特殊与一般”的认识.【教学重点】正方形的定义和性质及正方形与平行四边形、矩形、菱形的联系.【教学难点】正方形与矩形、菱形的关系及正方形性质的灵活运用.一、创设情境,导入新课装修房子铺地面的瓷砖,大多是正方形的形状,它是什么样的四边形?它与平行四边形、矩形、菱形有什么关系?【教学说明】用学生比较熟悉的正方形物体入手,容易引起学生的注意,激发全体学生的学习热情,提高学习效率.教师讲课前,先让学生完成预习.二、思考探究,获取新知问题1 正方形的定义和性质做一做:同一张长方形纸片折出一个正方形(如右图所示).【教学说明】让学生在动手操作中对正方形产生感性认识,并感知正方形与矩形的关系.正方形是特殊的平行四边形,也是特殊的矩形、菱形,所以它具有这些图形的所有性质.小组交流,归纳总结.例:教材第73页“例1”【教学说明】综合运用正方形的性质进行有关的证明,一方面达到掌握新知的目的,另一方面发展了学生推理能力.问题2 正方形的判定说一说:教材第73页“说一说”【教学说明】归纳正方形的判定方法,使学生更好地了解矩形、菱形、正方形之间的联系与区别,体验事物之间是相互联系但又是有区别的,同时也培养了学生善于归纳、勤于总结的好习惯.例:教材第73页“例2”【教学说明】引导学生运用所学知识解决问题,并学会一题多解,一题多变,养成勤于反思、归纳的好习惯.三、运用新知,深化理解1.如图所示,在正方形ABCD中,点E、F分别在CD、BC上,且BF=CE,连接BE、AF相交于点G,则下列结论不正确的是()A.BE=CEB.∠DAF=∠BECC.∠AFB+∠EBC=90°D.AG⊥BE2.已知四边形ABCD中,∠A=∠B=∠C=90°,如果添加一个条件,即可推出该四边形是正方形,那么这个条件可以是()A.∠D=90°B.AB=CDC.AD=BCD.BC=CD3.如图,点E是正方形ABCD的边BC延长线上的点,且CE=CA.(1)求∠ACE、∠CAE的度数;(2)若CD=5cm,请求出△ACE的面积.4.如图,在四边形ABCD中,点E是线段AD上的任意一点(E与A、D不重合),G 、F 、H 分别是BE 、BC 、CE 的中点.(1)求证:四边形EGFH 是平行四边形.(2)若EF ⊥BC ,且EF=21BC ,求证:平行四边形EGFH 是正方形. 【教学说明】让学生自主完成,检查学生掌握情况如何,根据情况个别辅导,对于出现错误较多的地方应作重点强调,有针对性加强训练.在完成上述题目后,让学生完成练习册中本课时的对应训练部分.答案:1.A 2.D 3.(1)∠ACE=135°,∠CAE=22.5°;(2)2225cm 2 4.证明:(1)在△BEC 中,∵G 、F 分别是BE 、BC 的中点,∴GF ∥EC 且GF=21EC , 又∵H 是EC 的中点,∴EH=21EC , ∴GF ∥EH 且GF=EH ,∴四边形EGFH 是平行四边形.(2)∵G 、H 分别是BE 、EC 的中点,∴GH ∥BC 且GH=21BC , 双∵EF ⊥BC 且EF=21BC , ∴EF ⊥GH ,EF=GH ,∴平行四边形EGFH 是正方形.四、师生互动,课堂小结这一节课的学习,你能完整地说出正方形的性质与判定吗?有哪些收获?还存在哪方面的问题?请与大家交流.【教学说明】归纳总结所学知识,形成结构体系,分享收获,探讨不足,以达到整体提高.1.布置作业:习题2.7中的第2、3题.2.完成练习册中本课时练习的作业部分.本节课虽然是学习正方形的性质与判定,实际上应起到对平行四边形、矩形、菱形性质和判定的复习、归纳和总结的作用,因此在教学中通过折纸、观察、验证推理等过程,使学生感受到了解它们之间的共同性质和判定与特殊性质和判定,理解更加深刻,运用更加熟练.。
专题2.13正方形(知识讲解)-八年级数学下册基础知识专项讲练(湘教版)

专题2.13 正方形(知识讲解)【学习目标】1.理解正方形的概念,了解平行四边形、矩形及菱形与正方形的概念之间的从属关系;2.掌握正方形的性质及判定方法.【要点梳理】要点一、正方形的定义四条边都相等,四个角都是直角的四边形叫做正方形.要点诠释:既是矩形又是菱形的四边形是正方形,它是特殊的菱形,又是特殊的矩形,更为特殊的平行四边形,正方形是有一组邻边相等的矩形,还是有一个角是直角的菱形.要点二、正方形的性质正方形具有四边形、平行四边形、矩形、菱形的一切性质.1.边——四边相等、邻边垂直、对边平行;2.角——四个角都是直角;3.对角线——①相等,②互相垂直平分,③每条对角线平分一组对角;4.是轴对称图形,有4条对称轴;又是中心对称图形,两条对角线的交点是对称中心.要点诠释:正方形具有平行四边形、矩形、菱形的一切性质,其对角线将正方形分为四个等腰直角三角形.要点三、正方形的判定正方形的判定除定义外,判定思路有两条:或先证四边形是菱形,再证明它有一个角是直角或对角线相等(即矩形);或先证四边形是矩形,再证明它有一组邻边相等或对角线互相垂直(即菱形).要点四、特殊平行四边形之间的关系或者可表示为:要点五、顺次连接特殊的平行四边形各边中点得到的四边形的形状(1)顺次连接平行四边形各边中点得到的四边形是平行四边形.(2)顺次连接矩形各边中点得到的四边形是菱形.(3)顺次连接菱形各边中点得到的四边形是矩形.(4)顺次连接正方形各边中点得到的四边形是正方形.要点诠释:新四边形由原四边形各边中点顺次连接而成.(1)若原四边形的对角线互相垂直,则新四边形是矩形.(2)若原四边形的对角线相等,则新四边形是菱形.(3)若原四边形的对角线垂直且相等,则新四边形是正方形.【典型例题】类型一、正方形的性质1、如图,在正方形ABCD中,点P是对角线AC上一点,连接PB、PD,点E在BC 的延长线上,且P E=PB.求证:(1)△BCP△△D CP;(2)△DPE =△ABC.【思路点拨】(1)根据正方形的四条边都相等可得BC=DC,对角线平分一组对角可得△BCP=△DCP,然后利用“边角边”证明即可;(2)根据全等三角形对应角相等可得△CBP=△CDP,根据等边对等角可得△CBP=△E,然后根据等角的余角得出△DPE= 90°,从而得证;【解析】证明:(1)△四边形ABCD是正方形△BC=DC,△ACB=△ACD ,△ABC=90°又△PC = PC△△BCP△△D CP.(2)△P E=PB,△△E=△PBE ,△△BCP△△D CP,△△PBE=△PDC ,△△E=△PDC ,△△E+△1=90°,△1=△2△△PDC+△2=90°即△DPE=90°△△DPE=△ABC.【总结升华】本题考查了正方形的性质,全等三角形的判定与性质,等边对等角的性质,熟记正方形的性质确定出△BCP=△DCP是解题的关键.举一反三:【变式1】如图,已知正方形ABCD的面积是8,连接AC、BD交于点O,CM平分△ACD 交BD于点M,MN△CM,交AB于点N,(1)求△BMN的度数;(2)求BN的长.【答案】(1)22..5°;(2)4【思路点拨】(1)先由正方形ABCD的面积是8,求得正方形的边长及其对角线的长;再由正方形的性质及CM平分△ACD,求得△DCO、△BCO、△CDO、△MBN、△DCM、△MCO及△BMC的度数;然后由MN△CM得△CMN=90°,则△BMN的度数等于△CMN的度数减去△BMC即可得出答案;(2)先证明△BCM=△BMC,从而可得BM=BC=CD,则由DM=BD﹣BM可得DM的长;【解析】解:(1)△正方形ABCD的面积是8,△BC=CD,△BD=4.△四边形ABCD为正方形,△△DCO=△BCO=△CDO=△MBN=45°,△CM平分△ACD,△△DCM=△MCO=22.5°,△△BMC=△CDO+△DCM=45°+22.5°=67.5°.△MN△CM,△△CMN=90°,△△BMN=90°﹣67.5°=22.5°,△△BMN的度数为22..5°.(2)△△MCO=22.5°,△BCO=45°,△△BCM=△BCO+△MCO=67.5°,又△△BMC=67.5°,△△BCM =△BMC ,△BM =BC =CD =,△DM =BD ﹣BM =4﹣.△△DCM =22.5°,△BMN =22.5°,△△DCM =△BMN .△在△DCM 和△BMN 中,DCM BMN DC BM CDM MBN ∠=∠⎧⎪=⎨⎪∠=∠⎩△△DCM △△BMN (ASA ),△BN =DM =4﹣△BN 的长为4﹣【总结升华】本题考查正方形的性质、角平分线的性质、余角的性质、全等三角形的判定与性质等知识,是重要考点,难度较易,掌握相关知识是解题关键.【变式2】已知,如图,在Rt△ABC 中,△BAC =90°,△ABC =45°,点D 为直线BC 上一动点(点D 不与点B ,C 重合).以AD 为边作正方形ADEF ,连接CF ,当点D 在线段BC 的反向延长线上,且点A ,F 分别在直线BC 的两侧时.(1)求证:△ABD △△ACF ;(2)若正方形ADEF的边长为对角线AE ,DF 相交于点O ,连接OC ,求OC 的长度.【思路点拨】(1)由题意易得AD =AF ,△DAF =90°,则有△DAB =△F AC ,进而可证AB =AC ,然后问题可证;(2)由(1)可得△ABD △△ACF ,则有△ABD =△ACF ,进而可得△ACF =135°,然后根据正方形的性质可求解.【解析】(1)证明:△四边形ADEF为正方形,△AD=AF,△DAF=90°,又△△BAC=90°,△△DAB=△F AC,△△ABC=45°,△BAC=90°,△△ACB=45°,△△ABC=△ACB,△AB=AC,△△ABD△△ACF(SAS);(2)解:由(1)知△ABD△△ACF,△△ABD=△ACF,△△ABC=45°,△△ABD=135°,△△ACF=135°,由(1)知△ACB=45°,△△DCF=90°,△正方形ADEF边长为△DF=4,△OC=12DF=12×4=2.【总结升华】本题主要考查正方形的性质及等腰直角三角形的性质,熟练掌握正方形的性质及等腰直角三角形的性质是解题的关键.类型二、正方形的判定2、如图,在平行四边形ABCD中,AE是BC边上的高,将ABE△沿BC方向平移,使点E与点C重合,得GFC.(1)求证:BE DG =;(2)若60B ∠=︒,当BC =______AB 时,四边形ABFG 是菱形;(3)若60B ∠=︒,当BC =______AB 时,四边形AECG 是正方形.【思路点拨】(1)根据平移的性质,可得:BE=FC ,再证明Rt△ABE△Rt△CDG 可得BE=DG ; (2)要使四边形ABFG 是菱形,须使AB=BF ;根据条件找到满足AB=BF 时,BC 与AB 的数量关系即可;(3)当四边形AECG 是正方形时,AE=EC ,由,可得,再有BE=12AB 可得AB . 【解析】(1)证明:△四边形ABCD 是平行四边形,△AD△BC ,AB=CD .△AE 是BC 边上的高,且CG 是由AE 沿BC 方向平移而成,△CG△AD ,AE=CG ,△△AEB=△CGD=90°.△在Rt△ABE 与Rt△CDG 中,AE CG AB CD =⎧⎨=⎩, △Rt△ABE△Rt△CDG (HL ),△BE=DG .(2)解:当BC=32AB 时,四边形ABFG 是菱形. 证明:△AB△GF ,AG△BF ,△四边形ABFG 是平行四边形.△Rt△ABE 中,△B=60°,△△BAE=30°, △BE=12AB (直角三角形中30°所对直角边等于斜边的一半),△BE=CF,BC=32 AB,△EF=12 AB.△AB=BF.△四边形ABFG是菱形.故答案是:32;(3)解:AB时,四边形AECG是正方形.△AE△BC,GC△CB,△AE△GC,△AEC=90°,△AG△CE,△四边形AECG是矩形,当AE=EC时,矩形AECG是正方形,△△B=60°,△EC=AE=2AB,BE=12AB,AB..【总结升华】本题考查了平行四边形的性质,正方形的判定,菱形的判定,以及直角三角形的性质.关键是熟练掌握菱形的判定定理,以及平行四边形的性质.【变式】如图所示,在四边形ABCD中,AD△BC,△B=90°,AD=24cm,BC=26cm动点P从点A出发沿AD方向向点D以1cm/s的速度运动,动点Q从点C出发沿着CB方向向点B以3cm/s的速度运动.点P,Q分别从点A和点C同时出发,当其中一点到达端点时,另一点随之停止运动.(1)经过多长时间,四边形PQCD是平行四边形?(2)经过多长时间,四边形PQBA是矩形?(3)若AB=8,如果Q点的移动速度不变,要使PQBA是正方形,则P点移动速度是多少?解:(1)△PD //CQ ,△只要当PD =CQ 时,四边形PQCD 是平行四边形,设运动时间为t ,24PD t =-,3CQ t =,列式:24﹣t =3t ,解得t =6,△经过6秒,四边形PQCD 是平行四边形;(2)△//AP BQ 且90B ∠=︒,△只要当AP =BQ 时,四边形PQBA 是矩形,设运动时间为t ,AP t =,263BQ t =-,列式:t =26﹣3t ,解得132t =, △经过132秒,四边形PQBA 是矩形; (3)当BQ =AB =8时,四边形PQCD 是正方形,设运动时间为t ,列式:26﹣3t =8,解得t =6,△P A =6•V P =8,△V P =43cm /s . 【总结升华】本题考查的是动点问题,涉及平行四边形的判定,矩形的判定,正方形的判定,解题的关键是设运动时间,用时间表示线段长度,然后根据题意列方程求解.类型三、正方形中的折叠问题3 如图,在边长为6的正方形ABCD 中,E 是边CD 的中点,将△ADE 沿AE 对折至△AFE ,延长EF 交边BC 于点G ,连接AG .(1)求证:△ABG△△AFG ;(2)求△EAG 的度数;(3)求BG 的长.【分析】(1)利用翻折变换对应边关系得出AB =AF ,△B =△AFG =90°,利用HL 定理得出△ABG△△AFG 即可;(2)由(1)可得△FAG =12△BAF ,由折叠的性质可得△EAF =12△DAF ,继而可得△EAG =12△BAD =45°; (3)首先设BG =x ,则可得CG =6﹣x ,GE =EF +FG =x +3,然后利用勾股定理GE 2=CG 2+CE 2,得方程:(x +3)2=(6﹣x )2+32,解此方程即可求得答案.【解析】(1)证明;在正方形ABCD 中,AD =AB =BC =CD ,△D =△B =△BCD =90°, △将△ADE 沿AE 对折至△AFE ,△AD =AF ,DE =EF ,△D =△AFE =90°,△AB =AF ,△B =△AFG =90°,又△AG =AG ,在Rt△ABG 和Rt△AFG 中,AG=AG AB=AF⎧⎨⎩, △△ABG△△AFG (HL );(2)△△ABG△△AFG ,△△BAG =△FAG ,△△FAG =12△BAF , 由折叠的性质可得:△EAF =△DAE , △△EAF =12△DAF , △△EAG =△EAF +△FAG =12(△DAF +△BAF )=12△DAB =12×90°=45°;(3)△E是CD的中点,△DE=CE=12CD=12×6=3,设BG=x,则CG=6﹣x,GE=EF+FG=x+3,△GE2=CG2+CE2△(x+3)2=(6﹣x)2+32,解得:x=2,△BG=2.【点拨】此题属于四边形的综合题,考查了正方形的性质、折叠的性质、全等三角形的判定与性质以及勾股定理等知识,注意折叠中的对应关系、注意掌握方程思想的应用是解此题的关键.【变式】如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交BC于点G,连接AG.(1)求证:△ABG△△AFG;(2)求BG的长.【答案】(1)证明见解析;(2)2.【分析】(1)利用翻折变换对应边关系得出AB=AF,△B=△AFG=90°,利用HL定理得出△ABG△△AFG即可;(2)利用勾股定理得出GE2=CG2+CE2,进而求出BG即可;【详解】(1)在正方形ABCD 中,AD=AB=BC=CD ,△D=△B=△BCD=90°,△将△ADE 沿AE 对折至△AFE ,△AD=AF ,DE=EF ,△D=△AFE=90°,△AB=AF ,△B=△AFG=90°,在Rt△ABG 和Rt△AFG 中,AG AG AB AF=⎧⎨=⎩, △Rt△ABG△Rt△AFG (HL );即△ABG△△AFG ;(2)△△ABG△△AFG ,△BG=FG ,设BG=FG=x ,则GC=6-x ,△E 为CD 的中点,△CE=EF=DE=3,△EG=3+x ,△在Rt△CEG 中,32+(6-x)2=(3+x)2,解得x=2,△BG=2.【点拨】本题主要考查了勾股定理的综合应用,全等三角形的判定和性质以及翻折变换的性质,根据翻折变换的性质得出对应线段相等是解题关键.类型四、正方形中的最值问题4.如图,在边长为2cm 的正方形ABCD 中,Q 为BC 边的中点,P 为对角线AC 上的一个动点,连接PB ,PQ ,求△PBQ 周长的最小值.【答案】1【分析】由于点B与点D关于AC对称,所以如果连接DQ,交AC于点P,由最短路径问题模型知,此时△PBQ的周长最小,△PBQ的周长=BP+PQ+BQ=DQ+BQ.在Rt△CDQ中,由勾股定理先计算出DQ的长度,再得出结果.解:连接DQ,交AC于点P,连接PB、BD,BD交AC于O.△四边形ABCD是正方形,△AC△BD,BO=OD,CD=2cm,△点B与点D关于AC对称,△BP=DP,△BP+PQ=DP+PQ=DQ.在Rt△CDQ中,由勾股定理,得QD==△△PBQ的周长的最小值为:(cm).【点拨】本图主要考查了正方形的性质,轴对称-最短路径问题,同时也考查了勾股定理得应用.是常考的基本题.【变式】如图,正方形ABCD中,AB=O是BC边的中点,点E是正方形内一动OE=,连接DE,将线段DE绕点D逆时针旋转90︒得DF,连接AE,CF.点,2(1)若A、E、O三点共线,求CF的长;(2)求CDF 的面积的最小值.【答案】(1)3;(2)10-【分析】(1)利用勾股定理求出AO 长,易得AE 长,由正方形的性质利用SAS 可证ADE CDF ≌,根据全等三角形对应边相等可得结论;(2)过点E 作EH AD ⊥于点H ,当,,O E H 三点共线,EH 最小,求出EH 长,根据三角形面积公式求解即可.解:(1)由旋转得:90EDF ∠=︒,ED DF =,△O 是BC 边的中点,△12BO BC == 在Rt AOB中,5AO ===.△523AE AO EO =-=-=.△四边形ABCD 是正方形,△90ADC ∠=︒,AD CD =,△ADC EDF ∠=∠,即ADE EDC EDC CDF ∠+∠=∠+∠,△ADE CDF ∠=∠.在ADE 和CDF 中AD CD ADE CDF DE DF =⎧⎪∠=∠⎨⎪=⎩△ADE CDF ≌.△3CF AE ==.(2)由于2OE =,所以E 点可以看作是以O 为圆心,2为半径的半圆上运动.过点E 作EH AD ⊥于点H .△ADE CDF ≌,△ADE CDF S S =△△当,,O E H 三点共线,EH 最小,2EH OH OE =-=.△1S 102CDF ADE S AD EH ==⨯⨯=-△△ 【总结升华】本题是正方形与三角形的综合题,涉及的知识点主要有正方形的性质、全等三角形的判定与性质、勾股定理,熟练的利用正方形的性质证明三角形全等是解题的关键.。
湘教版八年级数学下册课件-正方形

求证:四边形ABCD是正方形.
证明:∵四边形ABCD是矩形,
A
B
∴ AO=CO=BO=DO ,∠ADC=90°.
∵AC⊥DB,
O
∴ AD=AB=BC=CD,
D
C
∴四边形ABCD是正方形.
活动2 把可以活动的菱形框架的一个角变为直角,观 察这时菱形框架的形状.量量看是不是正方形.
正方形
猜想 满足怎样条件的菱形是正方形?
菱形
一个角是直角 对角线相等
正方 形
证一证
对角线相等的菱形是正方形. 已知:如图,在菱形ABCD中,AC , DB是它的两条对角线,
AC=DB.
求证:四边形ABCD是正方形. 证明:∵四边形ABCD是菱形, ∴AB=BC=CD=AD,AC⊥DB.
A
B
O
∵AC=DB, ∴ AO=BO=CO=DO,
D
B.对角线互相垂直平分
C.对角线平分一组对角
D.对角线相等
2.如图,四边形ABCD是正方形,对角线AC与 BD相交于点O,AO=2,求正方形的周长与面 积解.:∵四边形ABCD是正方形, ∴AC⊥BD,OA=OD=2. 在Rt△AOD中,由勾股定理,得
AD AO2 OD2 2 2, ∴正方形的周长为4AD=8 2 , 面积为AD2=8.
优质 课件
第2章 四边形
八年级数学下(XJ) 教学课件
2.7 正方形
导入新课
讲授新课
当堂练习
课堂小结
学习目标
1.探索并证明正方形的性质,并了解平行四边形、 矩形、菱形之间的联系和区别;(重点、难点)
2.探索并证明正方形的判定,并了解平行四边形、 矩形、菱形之间的联系和区别;(重点、难点)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课时教案
第节总序第节课题正方形复习编写时间月日执行时间月日
教学目标1、理解正方形的概念,了解正方形与平行四边形、菱形、矩形的关系.
2、掌握正方形的有关性质和判定方法.
3、能运用正方形的性质解决有关计算和证明问题.
重点、难点重点:正方形的性质和判定
难点:四边形成为正方形的条件
学具准备书本、笔、草稿纸、课堂点睛
教具准备Ppt、教案、课本、三角板、圆规
教学设计备注
一、复习引入
(1)、导言我们已学习了矩形、菱形,它们都是特殊的平行四边形.
(2)、1、让学生根据之前所学的知识分别叙述平行四边形/矩形、菱形的性质.
2、介绍平行四边形,矩形,菱形的内在联系.
Ⅲ、引人
[问题]根据小学学过的正方形的知识,四条边都相等,四个角都是直角的四边形是正方形,由同学
们来总结正方形的性质
边四条边相等
角四个角都是直角
对角线相等、垂直且互相平分平分一组对角
对称性轴对称图形
(3)根据正方形的性质,练习两道习题,并由同学们做出答案
1.正方形具有而菱形不一定具有的性质是()
A.对角线互相垂直
B.四条边都相等
C.对角线相等
D.对角线互相平分
2.正方形具有而矩形不一定具有的性质是()
A.对角线互相垂直
B.四个角都相等
C.对角线相等
D.对角线互相平分
二、新课讲解
复习前几节课的内容,如何判定矩形和菱形
如果四边形ABCD已经是一个矩形(或者菱形),那么再加上什么条件就可以变为正方形?小组讨论如何利用已知的图形,将矩形和菱形得到正方形
Ⅰ、正方形的判定
[探究] 操作 1 你能否利用手中的矩形白纸裁出一
个正方形呢?并请你把刚才所做的实验用图形表示
出来.并小组讨论,说说矩形与正方形的关系吗?
由同学们总结,正方形的判定定理:有一组邻边相等的矩
形是正方形.
[探究] 操作 2 你能否利用手中的可以活动的菱形模型
变成一个正方形吗?请演示并画出图形.
由同学们总结,正方形的判定定理:有一个角是直角的菱形是正方形.
根据上两条判定定理,总结出:有一个角是直角,并有一组邻边相等的平行四边形是正方形。
根据正方形的判定,练习一道习题,并由同学们做出答案
下列说法正确的是()
A.四条边相等的四边形是正方形
B.两条对角线互相垂直的矩形是正方形
C.两条对角线相等且互相垂直的四边形是正方形
D.两条对角线分别平分一组对角的四边形是正方
形
再练习两道证明题,巩固正方形的性质和判定方法
的相关知识,由同学们独立解答,并书写证明过程
[归纳]正方形与矩形、菱形、平行四边形间的关系如图.
Ⅱ、正方形的性质
正方形具有平行四边形、矩形、
菱形的一切性质.利用表格直观
的的在复习平行四边形、矩形、
菱形、正方形的性质,由同学将
表格完善,并从中熟记正方形的
性质
三、课堂总结
通过这节课的学习,同学们
有哪些收获?
引导学生从知识内容、数学思想方法两方面进行小结.
完善正方形的性质与平行四边形、矩形、菱形的转化过程,作为课后思考作业
正方形与矩形,菱形,平行四边形的关系.
教学
反思。
