排队论案例
合集下载
【最新精选】排队论习题
排队论习题1、某大学图书馆的一个借书柜台的顾客流服从泊松流，平均每小时50人，为顾客服务的时间服从负指数分布，平均每小时可服务80人，求：（1）顾客来借书不必等待的概率3/8（2）柜台前平均顾客数5/3（3）顾客在柜台前平均逗留时间1/30（4）顾客在柜台前平均等待时间1/802、一个新开张的理发店准备雇佣一名理发师，有两名理发师应聘。
由于水平不同，理发师甲平均每小时可服务3人，雇佣理发师甲的工资为每小时14元，理发师乙平均每小时可服务4人，雇佣理发师乙的工资为每小时20元，假设两名理发师的服务时间都服从负指数分布，另外假设顾客到达服从泊松分布，平均每小时2人。
问：假设来此理发店理发的顾客等候一小时的成本为30元，请进行经济分析，选出一位使排队系统更为经济的理发师。
3、一个小型的平价自选商场只有一个收款出口，假设到达收款出口的顾客流为泊松流，平均每小时为30人，收款员的服务时间服从负指数分布，平均每小时可服务40人。
（1）计算这个排队系统的数量指标P0、L q、L s、W q、W s。
（2）顾客对这个系统抱怨花费的时间太多，商店为了改进服务准备队以下两个方案进行选择。
1）在收款出口，除了收款员外还专雇一名装包员，这样可使每小时的服务率从40人提高到60人。
2）增加一个出口，使排队系统变成M/M/2系统，每个收款出口的服务率仍为40人。
对这两个排队系统进行评价，并作出选择。
4、汽车按泊松分布到达某高速公路收费口，平均90辆/小时。
每辆车通过收费口平均需时间35秒，服从负指数分布。
司机抱怨等待时间太长，管理部门拟采用自动收款装置使收费时间缩短到30秒，但条件是原收费口平均等待车辆超过6辆，且新装置的利用率不低于75%时才使用，问上述条件下新装置能否被采用。
5、有一台电话的共用电话亭打电话的顾客服从λ=6个/小时的泊松分布，平均每人打电话时间为3分钟，服从负指数分布。
试求：（1）到达者在开始打电话前需等待10分钟以上的概率（2）顾客从到达时算起到打完电话离去超过10分钟的概率（3）管理部门决定当打电话顾客平均等待时间超过3分钟时，将安装第二台电话，问当λ值为多大时需安装第二台。
排队论案例
第五节 排队论在生产中的应用
例三 降低在制品库存
方案1 是略微降低冲压机的压力（ 方案1 是略微降低冲压机的压力（这会导致冲压一套机翼组件的平均时间 增加到1 小时） 使得质检员可以更好地跟上它们的产出速度。 增加到1.2小时），使得质检员可以更好地跟上它们的产出速度。这还 会将每一台冲压机的成本（运作成本加折旧成本）从每小时7 会将每一台冲压机的成本（运作成本加折旧成本）从每小时7美元降低 到6.5美元。（相反，增大最大压力会使成本上升到7.5美元每小时， 美元。 相反， 增大最大压力会使成本上升到7 美元每小时， 冲压一套机翼组件的平均时间减低到0 小时。 冲压一套机翼组件的平均时间减低到0.8小时。） 方案2 是用一个年纪较轻的质检员做这项工作。他的工作速度比较快（ 方案2 是用一个年纪较轻的质检员做这项工作。他的工作速度比较快（尽 管由于缺少经验，检查时间有一些波动），因此他能够更好地跟上冲 管由于缺少经验， 检查时间有一些波动） 压机的产出速度。 他的检查时间服从均值为7 分钟， 压机的产出速度 。 （ 他的检查时间服从均值为 7 . 2 分钟 ， 服从指数分 这个质检员的工作等级要求每小时的收入为19 美元（ 19美元 布 ） 。 这个质检员的工作等级要求每小时的收入为 19 美元 （ 包括奖 现在地质检员由于工作等级较低，每小时17美元。 17美元 金），现在地质检员由于工作等级较低，每小时17美元。 你是杰里的工作人员中的管理科学专家， 你是杰里的工作人员中的管理科学专家，被要求对这个问题进行分 他要求你“ 析。他要求你“用最先进的管理科学技术分析每一个方案能够降低多 少在制品库存，然后提出你的建议。 少在制品库存，然后提出你的建议。”
第五节 排队论在生产中的应用
c. 方案 的求解结果 方案2的求解结果 系统1 系统 在制品库存(张, 件) 在制品库存 张 在系统中的数量 等待时间(h) 等待时间 一件产品在系统中的 时间(h) 时间 成本(美元 美元/h) 成本 美元 0.52 7.52 0.074 1.074 130.14 系统2 系统 4.41 5.25 0.63 0.75 61 合计 4.93 12.77 0.7 1.82 191.14
[指导]排队论算例
![[指导]排队论算例](https://img.taocdn.com/s3/m/354d731903020740be1e650e52ea551810a6c9d6.png)
排队论算例解：先根据每个状态的平衡条件建立状态方程组如下：1241)1(1)1(24)1(5)1(6)1(12)1()()1(5)4()1(6)3()1(12)2()1()1()1(3)3(2)4(1)4(2)2(1)3(2)4(2)1(2)2(1)4(1)1(3)1(241===+++=⎪⎪⎩⎪⎪⎨⎧====⎪⎪⎩⎪⎪⎨⎧+=+=+==+∑=P P P P P P i P P P P P P P P P P P P P P P P P P P P P i 由正则条件知：解得：076.0)0(8116)4(114.0)0(278)3(171.0)0(94)2(256.0)0(32)1(384.0)0(1)0(81211)0(8116)0(278)0(94)0(32)0()(81340===========++++=∑=P P P P P P P P P P P P P P P i P i 由正则条件知：【例题4】求解下列生灭过程的状态指标？解：系统容量有限，即最多可同时容纳3个顾客。
系统中可能容纳0个、1个、2个和3个顾客，即有4个状态。
对于状态0S 有：1032P P =，即：0132P P=对于状态1S 有：120542P P P =+，即：0231P P =对于状态3S 有：3232P P =，即：0192P P=由正则条件可知，13210=+++P P P P ，即：45.00=P故有：30.00=P 、15.02=P 、10.03=P。
【例题5】某公路收费入口处设有一收费亭，汽车进入公路必须向收费亭交费。
收费亭的收费时间服从负指数分布，平均每辆汽车的交费时间为7.2s ，汽车的到达率为400辆/h ，服从泊松分布。
试求：（1）收费亭空闲的概率；（2）收费亭前没有车辆排队的概率；（3）收费亭前排队长度超过100m （即排队车辆超过12辆）的概率；（4）平均排队长度；（5）车辆通过收费亭所花费时间的平均值；（6）车辆的平均排队时间？解：显然这是一个M/M/1/∞∞/排队系统，收费亭是服务台，汽车是顾客，汽车向收费亭交费便是接受服务。
排队论(Lingo方法)
线性规划
01
Lingo方法是线性规划的一种求解算法，可以用于求解排队论中
的优化问题。
迭代法
02
对于一些复杂的问题，可以使用迭代法结合Lingo方法进行求解，
以逐步逼近最优解。
启发式算法
03
对于一些大规模问题，可以使用启发式算法结合Lingo方法进行
求解，以提高求解效率。
04
Lingo方法在排队论中的 案例分析
Lingo方法在排队论中的优化问题
最小化等待时间
通过Lingo方法，可以优化等待时间，以最小化顾 客或任务的等待时间。
最小化队列长度
通过Lingo方法，可以优化队列长度，以最小化等 待空间的使用。
最大化服务台效率
通过Lingo方法，可以优化服务台效率，以提高服 务台的工作效率。
Lingo方法在排队论中的求解算法
等问题。
计算机科学
排队论用于研究计算机 网络的性能分析、负载 均衡和分布式系统等问
题。
排队论的发展历程
1903年，费尔南多·柯尔莫哥洛夫提出概率论的公理化 体系，为排队论奠定了理论基础。
1950年代，肯德尔提出了肯德尔模型，为多服务台排 队模型奠定了基础。
1930年代，厄兰格和朱伯夫提出了厄兰格模型，为单 服务台排队模型奠定了基础。
Lingo方法的适用范围
Lingo方法适用于各种线性规划问题，包括生产计划、资源分 配、运输问题等。
尤其适用于具有大量约束条件和决策变量的复杂问题，能够 有效地解决这些问题的最优解。
Lingo方法的优势和局限性
Lingo方法的优势在于它能够处理大规模的线性规划问题，并且具有较高的计算效率和精度。此外，Lingo方法还具有灵活性 和通用性，可以应用于各种不同的领域和问题。
排队论详解及案例
cmLiu@shufe
Operations Research
9.2 几个常用的概率分布
9.2.1 经验分布 9.2.2 泊松分布 9.2.3 负指数分布 9.2.4 爱尔朗分布
cmLiu@shufe
Operations Research
9.2.1 经验分布
主要指标
平均间隔时间 = 总时间 到达顾客总数
Operations Research
9.1.3 排队论研究的基本问题
（3）系统优化问题的研究 研究排队系统的目的就是通过对该系统概率规律的研究， 实现系统的优化。系统的优化包括最优设计和最优运营问 题。前者属于静态问题，它是在输入和服务参数给定的情 况下，确定系统的设计参数，以使服务设施达到最大效益 或者服务机构实现最为经济。后者属于动态问题，它是指 对于一个给定的系统，在系统运行的参数可以随着时间或 状态变化的情况下，考虑如何运营使某个目标函数达到最 优。
cmLiu@shufe
Operations Research
9.1.1 排队系统的描述和组成
一般的排队过程可以这样描述：顾客由顾客源出发，到达 服务机构（服务台、服务员）前，按排队规则排队等待接 受服务，服务机构按服务规则给顾客服务，顾客接受完服 务后就离开。
cmLiu@shufe
Operations Research
9.1.1 排队系统的描述和组成
尽管排队系统是多种多样的，但所有的排队系统都是由输入过程、排 队规则、服务机构及服务规则三个基本部分组成的。 （1）输入过程 描述顾客来源以及顾客到达排队系统的规律。 一般从以下几个方面对输入过程进行描述：顾客源中顾客的数量是 有限还是无限；顾客到达的方式是单个到达还是成批到达；顾客的到 达是否相互独立（以前到达的顾客对以后达到的顾客没有影响，则称 顾客的达到是相互独立的，否则就是有关联的）；顾客相继到达的间 隔时间分布是确定型的还是随机型的（如果是随机分布，需要知道单 位时间内的顾客到达数或者顾客相继到达时间间隔的概率分布）；输 入的过程是平稳的还是非平稳的（若相继到达的间隔时间分布参数 （如期望值、方差等）都是与时间无关的，则称输入过程是平稳的， 否则称为非平稳）。 本章主要讨论顾客的到达是相互独立的、输入过程是平稳的情形。
运筹学排队论
降低平均服务时间
降低服务时间旳可变性
增长服务人员
降低平均到达人数
经过顾客预约等方法来降低到达旳可变性
集中使用服务资源
更加好地计划和调度
23
处理排队问题旳措施
2.其他措施
服务场合提供娱乐设施
医生等待室放报纸杂志
自动维修间用收音机或电视
航空企业提供空中电影
等待电梯处放镜子
超级市场把冲动性商品摆放在收款台附
排队论
1
2
•
排队论，又称随机服务系统理论(,是一
门研究拥挤现象(排队、等待)旳科学。详细
地说，它是在研究多种排队系统概率规律性
旳基础上，处理相应排队系统旳最优设计和
最优控制问题。
•排队论是1923年由丹麦工程师爱尔朗
(A.K．Erlang)在研究电活系统时创建旳.
3
案例-1 银行排队系统
4
案例-2 医院排队系统
用更快旳服务人员、机器或采用不同旳设施布局和政
策来影响顾客旳到达时间和服务时间。
9
1 排队论旳基本问题
1.1 排队论旳主要研究内容
• 数量指标
– 研究主要数量指标在瞬时或平稳状态下旳
概率分布及其数字特征，了解系统旳基本
运营特征。
• 统计推断
– 检验系统是否到达平稳状态；检验顾客到
达间隔旳独立性；拟定服务时间分布及参
数。
• 系统优化
– 系统旳最优设计和最优运营问题。
10
1.2排队论旳经济含义
• 排队问题旳关键问题实际上就是对不同
原因做权衡决策。管理者必须衡量为提
供更快捷旳服务（如更多旳车道、额外
旳降落跑道、更多旳收银台）而增长旳
42交通流理论排队论
Ek代表爱尔朗分布的输入或服务。 于是泊松输入、负指数分布服务，N个服务台的排 队系统可以写成M/M/N；
泊松输入、定长服务、单个服务台的系统可以写 成M/D/1。
同样可以理解M/ Ek /N，D/M/N…等符号的含义。
如果不附其它说明，则这种符号一般都指先到先 服务，单个服务通道的等待制系统。
3)排队系统的主要数量指标
d n
w d 1
四、M/M/N系统
1 .计算公式 在 M / M / N 排队系统中，服务通道 有 N 条，所以也叫“多通道 服务”系统。 设 为进入多通道服务系统 车辆的平均到达率，排 队行列从每个服务台 接受服务后的平均输出 率为 ，则每个服务台的平均 服务时间是 1 / 。 仍记 / ，则 / N 称为 M / M / N 系统的服务强度或交通 强度，亦可称 为饱和度。和 M / M / 1相仿，当 / N 1时系统是稳定的，否则 不稳定，排 队长度将趋向于无穷大 。
M / M / N 系统根据车辆排队方式 的不同，可分为： 1）单路排队多通道服务 ：指排成一个队等待数 条通道服务的情况，排 队 中头一车辆可视哪条通 道有空就到哪里去接受 服务；
2）多路排队多通道服务 的一队车辆服务，车辆 组成的系统，其计算公
：指每个通道各排一个 不能随意换队。此种情 式亦相同。
例：有一公路与铁路的交叉口，火车通过时，栅栏关闭的时
间 tr= 0.1h。已知公路上车辆以均一的到达率＝900(辆／h)
到达交叉口，而栅栏开启后排队的车辆以均一的离去率u＝ 1200(辆／h)离开交叉口。试计算由于关闭栅栏而引起的：
单个车辆的最长延误时间tm， 最大排队车辆数Q， 排队疏散时间t 0， 排队持续时间t j 受限车辆总数n，
泊松输入、定长服务、单个服务台的系统可以写 成M/D/1。
同样可以理解M/ Ek /N，D/M/N…等符号的含义。
如果不附其它说明，则这种符号一般都指先到先 服务，单个服务通道的等待制系统。
3)排队系统的主要数量指标
d n
w d 1
四、M/M/N系统
1 .计算公式 在 M / M / N 排队系统中，服务通道 有 N 条，所以也叫“多通道 服务”系统。 设 为进入多通道服务系统 车辆的平均到达率，排 队行列从每个服务台 接受服务后的平均输出 率为 ，则每个服务台的平均 服务时间是 1 / 。 仍记 / ，则 / N 称为 M / M / N 系统的服务强度或交通 强度，亦可称 为饱和度。和 M / M / 1相仿，当 / N 1时系统是稳定的，否则 不稳定，排 队长度将趋向于无穷大 。
M / M / N 系统根据车辆排队方式 的不同，可分为： 1）单路排队多通道服务 ：指排成一个队等待数 条通道服务的情况，排 队 中头一车辆可视哪条通 道有空就到哪里去接受 服务；
2）多路排队多通道服务 的一队车辆服务，车辆 组成的系统，其计算公
：指每个通道各排一个 不能随意换队。此种情 式亦相同。
例：有一公路与铁路的交叉口，火车通过时，栅栏关闭的时
间 tr= 0.1h。已知公路上车辆以均一的到达率＝900(辆／h)
到达交叉口，而栅栏开启后排队的车辆以均一的离去率u＝ 1200(辆／h)离开交叉口。试计算由于关闭栅栏而引起的：
单个车辆的最长延误时间tm， 最大排队车辆数Q， 排队疏散时间t 0， 排队持续时间t j 受限车辆总数n，
运筹学——排队论
1 对于泊松流， λ表示单位时间内平均到 达的顾客数，因此， 就表示
λ
相继顾客到达的平均间 隔时间，这与 E[T ] =
1
λ
的意义正好相符。
18
服务时间v的分布 对一顾客的服务时间（也即在忙期相继离开系统的两顾客的间隔时间） 有时也服从负指数分布。这时设它的分布函数和密度函数分别为 Fv (t ) = 1 − e − µt , v的期望值 E (v) = 1 f v (t ) = µe − µt
期望值和方差相等，是泊松分布的一个重要特征，可以由此对一个 经验分布是否是泊松分布进行初步的识别。
16
3、负指数分布（negtive exponential distribution）
随机变量T的概率密度若是 λe −λt , t ≥ 0 fT (t ) = 0, t < 0 则称T服从负指数分布。T 分布函数是 1 − e −λt , t ≥ 0 FT (t ) = 0, t < 0 E[T ] = 1
∞
∑ P (t , t + ∆t ) = o( ∆t )
n=2 n
15
通过建立Pn (t )与Pn (t + ∆t )之间的关系方程并求解，得到
( λ t ) n − λt Pn (t ) = e n! t > 0, n = 0,1,2,L
Pn (t ) = Pn (0, t )表示长为t的时间区间内到达n个顾客的概率，并称随机变量 N (t )服从泊松分布，其数学期望和方差分别为 E[ N (t )] = λt Var[ N (t )] = λt
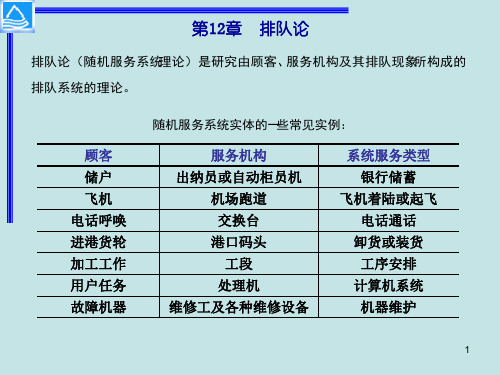
第12章 12章
排队论
排队论（随机服务系统理论）是研究由顾客、服务机构及其排队现象所构成的 排队系统的理论。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第五节 排队论在生产中的应用
d. 推荐方案 增加压力, 并起用年轻质检员, 增加压力 并起用年轻质检员 求解结果如下 系统1 系统 在制品库存(张, 件) 在制品库存 张 在系统中的数量 等待时间(h) 等待时间 一件产品在系统中的 时间(h) 时间 成本(美元 美元/h) 成本 美元 0.09 5.69 0.013 0.813 120.51 系统2 系统 4.41 5.25 0.63 0.75 61 合计 4.5 10.94 0.64 1.56 181.51
第五节 排队论在生产中的应用
现状求解结果 系统1 系统 在制品库存(张, 件) 在制品库存 张 在系统中的数量 等待时间(h) 等待时间 一件产品在系统中的 时间(h) 时间 成本(美元 美元/h) 成本 美元 0.52 7.52 0.074 1.074 130.14 系统2 系统 6.13 7 0.875 1 73 合计 6.65 14.52 0.95 2.07 203.14
第五节 排队论在生产中的应用
例三 降低在制品库存
a. 为了提供一个比较的基础，首先要评价现在的状态。确定 为了提供一个比较的基础， 首先要评价现在的状态。 在冲压机那里和质检站的在制品期望库存量。 在冲压机那里和质检站的在制品期望库存量。 然后计算在 制品库存、冲压机、质检员每小时期望总成本。 制品库存、冲压机、质检员每小时期望总成本。 方案1会有什么影响？为什么？将得到的结果与a b. 方案 1 会有什么影响 ？ 为什么 ？ 将得到的结果与 a 的结果进 行细致的比较。将结果解释给杰里听。 行细致的比较。将结果解释给杰里听。 方案2会有什么影响？为什么？将得到的结果与a c. 方案 2 会有什么影响 ？ 为什么 ？ 将得到的结果与 a 的结果进 行细致的比较。将结果解释给杰里听。 行细致的比较。将结果解释给杰里听。 对于降低在冲压机那里和质检站的在制品期望库存量， d. 对于降低在冲压机那里和质检站的在制品期望库存量 ， 提 出你的建议方案。明确说出你的方案，并用象a 出你的建议方案。明确说出你的方案，并用象a一样的量化 分析为你的方案提供支持。将得到的结果与a 分析为你的方案提供支持。将得到的结果与a的结果进行细 致的比较，并表示出你建议的方案将产生的改进效果。 致的比较，并表示出你建议的方案将产生的改进效果。
第五节 排队论在生产中的应用
例三 降低在制品库存
委屈的杰里努力回答： 是的，吉姆， 委屈的杰里努力回答：“是的，吉姆，我已经意识到了质 检站是一个瓶颈。它通常不像你早上看到的那样糟， 检站是一个瓶颈。它通常不像你早上看到的那样糟，但 是它的确是一个瓶颈。 是它的确是一个瓶颈 。 早上你看到的的确是较差的情 况。” 希望如此， 吉姆反驳道， “希望如此，”吉姆反驳道，“但是你应当防止这种情况 的发生，哪怕是偶然发生。你准备怎么做？ 的发生，哪怕是偶然发生。你准备怎么做？” 杰里现在对他的提问有话可说了。 他说： 实际上， 杰里现在对他的提问有话可说了 。 他说 ： “ 实际上 ， 我已经在处理这个问题。我现在有一些方案，我要求我 我已经在处理这个问题。我现在有一些方案， 的工作人员的管理科学专家分析这些建议， 的工作人员的管理科学专家分析这些建议，然后提出建 议方案。 议方案。” 很好， 吉姆回答道， 高兴这个问题在你的掌握之中。 “很好，”吉姆回答道，“高兴这个问题在你的掌握之中。 授予你最高的优先权，尽可能快地向我报告。 授予你最高的优先权，尽可能快地向我报告。” 我会这样做的， 杰里保证。 “我会这样做的，”杰里保证。
第五节 排队论在生产中的应用
例三 降低在制品库存
方案1 是略微降低冲压机的压力（ 方案1 是略微降低冲压机的压力（这会导致冲压一套机翼组件的平均时间 增加到1 小时） 使得质检员可以更好地跟上它们的产出速度。 增加到1.2小时），使得质检员可以更好地跟上它们的产出速度。这还 会将每一台冲压机的成本（运作成本加折旧成本）从每小时7 会将每一台冲压机的成本（运作成本加折旧成本）从每小时7美元降低 到6.5美元。（相反，增大最大压力会使成本上升到7.5美元每小时， 美元。 相反， 增大最大压力会使成本上升到7 美元每小时， 冲压一套机翼组件的平均时间减低到0 小时。 冲压一套机翼组件的平均时间减低到0.8小时。） 方案2 是用一个年纪较轻的质检员做这项工作。他的工作速度比较快（ 方案2 是用一个年纪较轻的质检员做这项工作。他的工作速度比较快（尽 管由于缺少经验，检查时间有一些波动），因此他能够更好地跟上冲 管由于缺少经验， 检查时间有一些波动） 压机的产出速度。 他的检查时间服从均值为7 分钟， 压机的产出速度 。 （ 他的检查时间服从均值为 7 . 2 分钟 ， 服从指数分 这个质检员的工作等级要求每小时的收入为19 美元（ 19美元 布 ） 。 这个质检员的工作等级要求每小时的收入为 19 美元 （ 包括奖 现在地质检员由于工作等级较低，每小时17美元。 17美元 金），现在地质检员由于工作等级较低，每小时17美元。 你是杰里的工作人员中的管理科学专家， 你是杰里的工作人员中的管理科学专家，被要求对这个问题进行分 他要求你“ 析。他要求你“用最先进的管理科学技术分析每一个方案能够降低多 少在制品库存，然后提出你的建议。 少在制品库存，然后提出你的建议。”
第五节 排队论在生产中的应用
例三 降低在制品库存
这里是杰里和他的管理科学专家们所遇到的问题: 这里是杰里和他的管理科学专家们所遇到的问题:。10 台一样的冲压机每一台都用于在一张经过特殊处理的金 属薄板上冲压出机翼组件。金属薄板以每小时7 属薄板上冲压出机翼组件 。 金属薄板以每小时7 张随机 到达。 到达。冲压机冲压出机翼组件的时间服从均值为一小时 地指数分布。完成后， 地指数分布。完成后，机翼组件以相同的到达率随机到 达质检站（每小时7 达质检站 （ 每小时 7 套 ） 。 一个质检员全职检查这些机 翼组件，保证它们符合标准。每次检查花费她7 分钟。 翼组件 ，保证它们符合标准 。 每次检查花费她 7.5 分钟 。 因此每小时她可以检查8套机翼组件。 因此每小时她可以检查 8 套机翼组件 。 除了在冲压机那 里已有的在制品库存外， 里已有的在制品库存外，这个检查率导致了质检站大量 的在制品库存（也就是说， 的在制品库存（也就是说，等待完成检查的机翼组件的 平均数量相当大） 平均数量相当大）。 这种在制品库存的成本估计是每一张在冲压机那里的金 属薄板或每一套在质检站的机翼组件每小时8美元。 属薄板或每一套在质检站的机翼组件每小时 8 美元 。 因 此杰里提出了两个方案以降低在制品库存的平均水平。 此杰里提出了两个方案以降低在制品库存的平均水平。
第五节 排队论在生产中的应用
b. 方案 的求解结果 方案1的求解结果 系统1 系统 在制品库存(张, 件) 在制品库存 张 在系统中的数量 等待时间(h) 等待时间 一件产品在系统中的 时间(h) 时间 成本(美元 美元/h) 成本 美元 2.65 11.05 0.38 1.58 153.38 系统2 系统 6.13 7 0.875 1 73 合计 8.78 18.05 1.255 2.58 225.38
第五节 排队论在生产中的应用
c. 方案 的求解结果 方案2的求解结果 系统1 系统 在制品库存(张, 件) 在制品库存 张 在系统中的数量 等待时间(h) 等待时间 一件产品在系统中的 时间(h) 时间 成本(美元 美元/h) 成本 美元 0.52 7.52 0.074 1.074 130.14 系统2 系统 4.41 5.25 0.63 0.75 61 合计 4.93 12.77 0.7 1.82 191.14
ቤተ መጻሕፍቲ ባይዱ
THE END
第五节 排队论在生产中的应用
例三
分析：该问题可以近似看成是两个独立的排队系统： 分析：该问题可以近似看成是两个独立的排队系统： 系统1 系统1： 机翼组件冲压系统 模型形式 M/M/c 系统2 系统2： 机翼组件检查系统 模型形式 M/M/1 M/M/1 a 现状研究 系统1 系统1参数 µ = 1张/台·h λ1=7张/h 张 h 美元/h /h； 美元/h /h； cS=7美元/h；cW=8美元/h； 系统2 系统2参数 λ2=8套 µ =7套/h λ2=8套/h 套 17美元/h； 美元/h 美元/h /h； cS=17美元/h；cW=8美元/h；
第五节 排队论在生产中的应用
例三 降低在制品库存
北方（Northern）飞机制造公司的制造副总裁吉姆·威尔士被激怒 北方（ Northern） 飞机制造公司的制造副总裁吉姆 威尔士被激怒 这个早晨他走过公司最重要的制造厂，使他情绪非常的差。 了 ， 这个早晨他走过公司最重要的制造厂 ， 使他情绪非常的差 。 但 是现在他可以将脾气发泄在这个厂的制造经理杰里·卡斯塔斯身上 卡斯塔斯身上。 是现在他可以将脾气发泄在这个厂的制造经理杰里 卡斯塔斯身上。 杰里刚刚被吉姆叫进办公室。 杰里刚刚被吉姆叫进办公室。 杰里，我刚刚从厂子那里回来，我非常失望。 “杰里，我刚刚从厂子那里回来，我非常失望。” 出了什么问题，吉姆？ “出了什么问题，吉姆？” 你知道我是多么地强调要削减我们的在制品库存。 “你知道我是多么地强调要削减我们的在制品库存。” 是的，我们一直在努力。 杰里回答道。 “是的，我们一直在努力。”杰里回答道。 还不够！ 吉姆提高了他的噪音。 “还不够！”吉姆提高了他的噪音。“你知道我在走过冲压机时看到了 什么吗？ 什么吗？” 不知道。 “不知道。” 张金属薄板等待加工成机翼组件。然后在旁边的质检站，放着13 “有5张金属薄板等待加工成机翼组件。然后在旁边的质检站，放着13 套机翼组件。一个质检员正在检查一套，其他12套却躺在那里。 12套却躺在那里 套机翼组件。 一个质检员正在检查一套 ， 其他 12 套却躺在那里 。 你 知道每一套机翼组件占用了我们几十万美元的资金。 知道每一套机翼组件占用了我们几十万美元的资金 。 因此在冲压机 和质检站间，有几百万美元的贵重金属躺在那儿。我不允许这样！ 和质检站间， 有几百万美元的贵重金属躺在那儿 。 我不允许这样！”