基于排队论的决策系统研究
排队管理及相关战略研究综述
排队管理及相关战略研究综述排队管理是指通过科学的方法和技术手段来使排队系统达到最优化的运行状态，提高服务效率和客户满意度。
排队管理的目标是在给定的资源限制下，尽可能地减少等待时间、提高服务质量和效率。
排队管理涉及到各个领域，包括交通运输、服务行业、医疗保健等。
排队管理的主要方法有排队论、模拟仿真和队列控制。
排队论是一种数学方法，通过计算和模型来预测和分析排队系统的性能和行为。
排队论可以帮助决策者确定最佳的排队策略和资源配置，以达到最优的排队效果。
模拟仿真是通过建立排队系统的模型，进行虚拟实验和测试，以评估和比较不同的排队策略和控制方案的效果。
队列控制是一种实时的控制方法，通过监测和调整排队系统的运行状态，以及调整资源分配和服务策略，来优化排队效果。
在排队管理中，有一些常见的问题和挑战，包括队列长度、等待时间、服务效率、分流等。
解决这些问题的方法有单一排队系统、多排队系统、优先级排队系统、分流系统等。
单一排队系统是指只有一个排队队列和服务窗口，适用于服务窗口资源有限的场景。
多排队系统是指有多个排队队列和服务窗口，可以根据不同的优先级和需求来分配服务窗口，适用于许多实际场景。
优先级排队系统是指根据不同的优先级来分配服务顺序，比如VIP优先、老人孕妇优先等。
分流系统是指在排队系统前设置一个分流节点，根据不同的需求和资源来分流客户，减少排队长度和等待时间。
对于排队管理的战略研究，主要包括以下几个方面。
首先是资源分配和需求预测的研究。
资源分配是指如何合理地分配和利用排队系统的资源，包括服务窗口、人力和设备等。
需求预测是指如何准确地预测客户的到达和需求，以便进行合理的资源配置和排队策略制定。
其次是排队策略的研究。
排队策略包括服务优先级、分流规则、队列长度控制和等待时间控制等，通过制定合理的排队策略，可以有效地提高排队系统的效率和客户满意度。
最后是技术手段和工具的研究。
随着计算机和通信技术的发展，排队管理可以借助于各种技术手段和工具，如智能排队机器人、无人机服务等，来提高服务效率和客户体验。
基于随机过程和排队论的客流量预测模型研究
基于随机过程和排队论的客流量预测模型研究客流量预测是城市规划、交通管理和商业运营等领域重要的决策依据。
在过去几十年中，随机过程和排队论被广泛应用于客流量预测模型的研究和实践中。
本文将基于随机过程和排队论，探讨客流量预测模型的研究。
首先，介绍客流量预测的背景和意义。
客流量预测是指利用历史数据、实时采集的数据和其他相关信息，通过建立合理的数学模型和算法，对未来一段时间内的客流量进行预测。
这对于交通拥堵缓解、公共汽车和地铁的调度优化、商场的运营决策等都具有重要的意义。
其次，介绍随机过程在客流量预测中的应用。
随机过程是指一类随机变量组成的数列或随机函数，它们的值随时间的推移而变化。
在客流量预测中，可以使用随机过程来对客流量的变化进行建模。
例如，可以使用马尔可夫链来描述人群在不同地点之间的转移概率和持续时间，进而预测未来的客流量。
然后，介绍排队论在客流量预测中的应用。
排队论是研究排队系统的数学理论，可以帮助我们理解和优化排队现象。
在客流量预测中，可以使用排队论来模拟和分析客流量的到达和服务过程。
例如，可以使用M/M/1模型来预测某一时刻的客流量、平均排队长度和平均等待时间。
接下来，介绍基于随机过程和排队论的客流量预测模型的研究进展。
目前，已经有许多研究基于随机过程和排队论的方法提出了各种客流量预测模型。
这些模型包括马尔可夫链模型、M/M/1模型、基于时间序列的模型等。
其中，基于时间序列的模型在实际应用中较为常见，可以利用历史客流量数据进行参数估计和模型拟合，进而预测未来的客流量。
最后，总结基于随机过程和排队论的客流量预测模型的优点和不足。
随机过程和排队论能够提供可靠的理论基础和数学方法，帮助我们对客流量进行准确的预测和分析。
然而，这些模型往往依赖于许多假设和条件，对于复杂的客流量预测问题可能存在不足之处。
未来的研究可以进一步改进和拓展基于随机过程和排队论的客流量预测模型，提高其准确性和实用性。
综上所述，基于随机过程和排队论的客流量预测模型是客流量预测的重要研究方向。
基于排队论的资源调度策略研究
基于排队论的资源调度策略研究第一章：引言随着信息技术的快速发展和智能化时代的到来，资源调度问题成为了许多领域中的研究热点。
资源调度策略的优化对于提高效率、降低成本和优化服务质量具有重要的意义。
排队论作为一种重要的方法论，在资源调度问题中具有广泛的应用价值。
本文将基于排队论的方法，研究资源调度策略的优化问题，旨在提高系统的性能和效率。
第二章：排队论基础知识2.1 排队论概述排队论是一门研究顾客到达和等待的科学，它研究如何通过合理的资源调度和配置，提高系统的效率和性能。
2.2 排队系统的模型排队系统由三个基本部分组成：顾客的到达模型、服务设备和服务策略。
其中，顾客的到达模型可以采用泊松分布、负指数分布等数学模型进行描述；服务设备可以使用单一或多个服务台进行服务；而服务策略则包括先来先服务、最短作业优先等不同的调度规则。
2.3 排队系统的性能指标排队系统的性能指标可以通过排队长度、等待时间、客户满意度等指标进行度量，不同的应用场景对于性能指标的重要性也有所不同。
第三章：资源调度策略研究3.1 基于最短排队时间的调度策略最短排队时间调度策略是一种常见的资源调度策略，它通过选择排队时间最短的任务进行调度，以降低系统的等待时间和延迟。
3.2 基于服务质量的调度策略服务质量是资源调度中一个关键的指标，通过考虑任务的优先级、紧急程度、需求量等因素，采取不同的调度策略来提高服务质量和用户满意度。
3.3 基于负载均衡的调度策略负载均衡是在资源调度中常见的一种策略，通过合理地分配和调度资源，使系统中的负载尽量均衡，并优化系统的性能和效率。
第四章：实验与结果分析4.1 实验设计本文设计了一系列实验，通过模拟排队系统，对比不同的资源调度策略的性能和效果。
4.2 实验结果与分析通过对实验结果的分析，我们发现基于最短排队时间的调度策略能够有效地降低系统的等待时间和延迟；基于服务质量的调度策略能够提高用户的满意度和服务质量；基于负载均衡的调度策略能够优化系统的性能和效率。
DXC22基于排队论的服务系统优化研究以XX超市收银台为例
1、排队模型排队论是研究排队现象的理论与运用的学科，是专门研究由于随机因素的影响而产生的拥挤现象的科学，有人也称之为随机服务系统，或称之为公用事业的数学方法。
它是运筹学的一个重要的分支。
凡是出现拥挤现象的领域，都可以运用排队论。
在日常的生产和生活中有各种各样的随机服务系统，人们经常会碰到许多有形或无形的排队现象。
例如：到食堂打饭，到车站等车，去超市购物等等。
这些问题中，食堂的服务窗口与打饭者、公共汽车与乘客、超市收银台与购物者都可归结为服务窗口与顾客之间的一种服务关系，都可以当做排队问题来研究，他们之间就构成了一个排队系统或服务系统。
为了统一起见，我们把要求得到服务的对象统称为“顾客”，把提供服务的服务者称之为“服务员”、“服务窗口”、或“服务机构”。
因为顾客的到达情况和每位顾客接受服务的时间往往是无法事先知道的，或者说是随机的。
在排队论所研究的排队系统中，顾客相继到达时间间隔与服务时间这两个变量中至少有一个是随机的，因此排队论又称为随即服务系统理论。
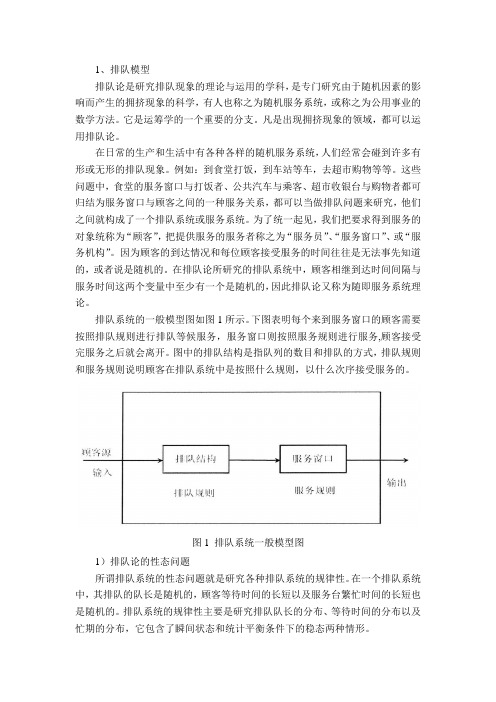
排队系统的一般模型图如图1所示。
下图表明每个来到服务窗口的顾客需要按照排队规则进行排队等候服务，服务窗口则按照服务规则进行服务,顾客接受完服务之后就会离开。
图中的排队结构是指队列的数目和排队的方式，排队规则和服务规则说明顾客在排队系统中是按照什么规则，以什么次序接受服务的。
图1 排队系统一般模型图1）排队论的性态问题所谓排队系统的性态问题就是研究各种排队系统的规律性。
在一个排队系统中，其排队的队长是随机的，顾客等待时间的长短以及服务台繁忙时间的长短也是随机的。
排队系统的规律性主要是研究排队队长的分布、等待时间的分布以及忙期的分布，它包含了瞬间状态和统计平衡条件下的稳态两种情形。
2）排队系统的最优化问题排队系统的最优化问题主要有两类：包括系统的最优化设计和系统的最优化运行控制。
前者又称为静态最优化，后者又称为动态最优化。
前者是在服务系统设置之前就对未来的运行情况进行估计，从而使设计人员有所依据。
基于排队论和整数规划的银行柜员弹性排班模型
基于排队论和整数规划的银行柜员弹性排班模型一、本文概述随着银行业务的日益发展和客户需求的多样化，银行柜员排班问题成为了银行业务运营中的关键环节。
传统的固定排班模式已难以满足现代银行业务的需求，因此，开发一种基于排队论和整数规划的银行柜员弹性排班模型显得尤为重要。
本文旨在探讨如何运用排队论和整数规划的理论和方法，构建一个既能满足客户需求，又能保证柜员工作效率和满意度的弹性排班模型。
排队论作为一种研究服务系统中排队现象的数学工具，可以分析客户到达和服务的统计规律，为银行柜员排班提供理论基础。
整数规划则是一种求解最优化问题的数学方法，通过约束条件和目标函数的设置，可以求得满足实际需求的柜员排班方案。
本文将首先介绍排队论和整数规划的基本原理及其在银行柜员排班中的应用背景，然后详细阐述基于排队论和整数规划的银行柜员弹性排班模型的构建过程，包括模型的假设、参数设定、约束条件构建以及目标函数的确定。
通过实例分析验证模型的有效性和实用性，并提出模型的改进方向和应用前景。
本文的研究不仅有助于提升银行柜员排班的科学性和合理性，还可以为银行业务的持续优化和客户服务质量的提升提供有力支持。
也为其他服务行业在弹性排班模型的构建和应用方面提供有益的参考和借鉴。
二、理论基础本研究所构建的银行柜员弹性排班模型主要基于两个理论基础：排队论和整数规划。
这两个理论在运筹学、管理科学和工程领域具有广泛的应用，尤其在处理资源优化配置和服务系统效率提升的问题上表现出色。
排队论，又称为随机服务系统理论，主要研究服务系统中等待队列的形成、发展和变化规律，以及系统的性能特征。
在银行柜员排班问题中，客户到达银行办理业务的过程就是一个典型的排队过程。
排队论中的关键概念包括顾客到达率、服务率等待时间、队列长度等，这些指标直接影响到银行的服务质量和顾客满意度。
通过排队论，我们可以对银行柜员的工作强度、服务效率以及顾客等待时间进行数学建模，为合理的排班安排提供理论支持。
运筹学中的排队论分析与应用
运筹学中的排队论分析与应用运筹学是一门研究如何最优化决策的学科。
在现代社会中，许多场景下都存在排队现象，例如银行、超市、机场等场所。
排队论作为运筹学的一个重要分支，专门研究如何通过合理的排队策略来优化服务效率与用户体验。
本文将介绍排队论的基本原理、应用场景以及如何利用排队论进行实际问题的分析与解决。
一、排队论的基本原理排队论是研究排队系统的理论与方法，其基本原理包括排队模型、排队规则以及排队指标。
1. 排队模型排队模型是对排队系统进行抽象和建模的过程，常用的排队模型有M/M/1、M/M/c、M/G/1等。
其中，M表示顾客到达过程符合泊松分布，而服务过程符合指数分布；1表示一个服务台，c表示多个服务台；G表示总体服从一般分布。
2. 排队规则排队规则是指在排队系统中，顾客到达和离开的规则。
常用的排队规则有先到先服务（First-Come-First-Serve，简称FCFS）、最短作业优先（Shortest Job First，简称SJF）、优先级法则等。
3. 排队指标排队指标是对排队系统性能的度量，常用的排队指标包括平均等待时间、平均逗留时间、系统繁忙度等。
这些指标可以帮助我们评估排队系统的效率，并进行比较和优化。
二、排队论的应用场景排队论的应用场景非常广泛，几乎可以涵盖各个行业。
下面以几个典型的应用场景为例，介绍排队论在其中的分析与应用。
1. 银行排队银行是排队论的典型应用场景之一。
通过排队论的分析，银行可以确定合理的柜台数量和工作人员配置，以减少客户的等待时间和提高服务效率。
此外，银行还可以考虑引入预约系统、自助服务等方式，进一步优化排队系统。
2. 售票窗口排队售票窗口也是一个常见的排队场景，如电影院、火车站等。
利用排队论，可以根据顾客到达的速率和服务时间的分布，预测等待时间，并提前安排足够的窗口进行服务，以提高售票效率和用户体验。
3. 交通信号灯优化交通信号灯的优化也可以借助排队论的方法。
通过对道路上车辆到达和通过的流量进行统计和分析，可以调整信号灯的信号周期和配时方案，以减少交通拥堵和减少等待时间。
排队论在交通控制系统中的应用研究
排队论在交通控制系统中的应用研究标题：排队论在交通控制系统中的应用研究摘要：随着城市人口的快速增长以及汽车保有量的不断增加，交通事故、拥堵和排队等问题日益突出。
针对这些问题，在交通控制系统中引入排队论来优化交通流。
本文通过概述排队论的基本概念和原理，探讨了排队论在交通控制系统中的应用研究。
具体而言，文章从排队系统建模、交通流量预测、信号调度优化以及自适应控制等四个方面阐述了排队论的应用。
还分析了相关研究中存在的问题，并提出了未来研究的方向和挑战。
关键词：排队论，交通流，交通控制，排队系统建模，信号调度优化。
第一部分：引言交通拥堵是城市化进程中普遍存在且日益严重的问题，对人们的工作、生活产生了严重的影响。
为了解决交通拥堵问题，研究者们引入排队论来优化交通控制系统。
排队论是研究顾客到达系统、排队与服务系统之间关系的学科，通过排队论在交通控制系统中的应用，可以提高交通流的稳定性和效率。
本文旨在探讨排队论在交通控制系统中的应用研究。
第二部分：排队论的基本概念和原理排队论是对排队系统中顾客到达、排队和服务之间关系的研究。
排队系统可以用一系列的随机过程来刻画。
排队论的主要目标是分析和优化排队系统中的性能指标，例如顾客等待时间、系统平均服务时间和服务设备利用率等。
在交通控制领域，排队论被广泛应用于优化交通信号的时序和策略。
第三部分：排队系统建模在交通控制系统中，排队系统的建模是实现排队论应用的基础。
将交通流视为到达系统，路段或十字路口作为服务设备，排队论可以用来描述交通拥堵和调度问题。
对于不同类型的路段和十字路口，可以采用不同的排队模型，如M/M/1模型、M/M/m模型等。
第四部分：交通流量预测交通流量的准确预测对于交通控制系统至关重要。
基于排队论的方法可以通过建立交通流量模型来进行预测，并根据预测结果进行信号控制调整。
通过对历史交通流量数据的分析和建模，可以获得交通流量在不同时间段和不同路段的变化规律，从而实现对交通信号灯的自适应调整，减少拥堵和排队现象。
排队论在服务系统优化中的运筹学方法研究
排队论在服务系统优化中的运筹学方法研究服务系统是现代社会中不可或缺的组成部分，如银行、医院、机场等各类场所的服务流程都需要进行优化，以提高效率和用户体验。
排队论作为运筹学的一个重要分支，研究如何合理组织和管理服务系统中的排队现象，对于服务系统优化具有重要意义。
本文将探讨排队论在服务系统优化中的运筹学方法。
一、排队论基本模型排队论是研究排队现象的一门学科，其基本模型由顾客到达过程、顾客排队等待过程和顾客接受服务过程组成。
下面我们将介绍三个基本模型。
1. M/M/1模型M/M/1模型是最简单的排队论模型，代表顾客到达过程和服务过程都符合随机过程。
其中的M表示到达过程和服务过程都满足泊松过程，/表示到达过程和服务过程是独立的，1表示只有一个服务台。
该模型可以通过计算平均等待时间、平均队长等指标，来评估系统的运行效果。
2. M/M/c模型M/M/c模型是多通道排队系统的模型，代表顾客到达过程和服务过程都符合随机过程，但服务台的数量有多个。
该模型可以用于评估多个服务台的效率分配问题，提高服务系统的整体服务水平。
3. M/G/1模型M/G/1模型是顾客到达过程满足泊松分布，而服务过程满足一般分布的排队系统模型。
该模型相比于前两个模型更加复杂，但也更加接近现实服务系统的情况。
通过研究和优化M/G/1模型，可以为实际服务系统提供更准确的优化方案。
二、排队论方法在服务系统中的应用排队论方法在服务系统中的应用十分广泛，涉及到客户流量预测、服务水平评估、服务台数量决策等多个方面。
1. 客户流量预测客户流量预测是排队论方法在服务系统优化中的重要应用之一。
通过对历史数据的分析和建模，可以预测未来客户到达的概率分布，进而确定合理的服务台数量和服务水平指标。
例如，某银行可以通过排队论方法预测未来客户到达和离开的概率，从而优化柜员人数和窗口开放时间，提高客户满意度。
2. 服务水平评估排队论方法可以用于评估服务系统的服务水平，比如平均等待时间、平均队长等指标。
运筹学 排队论
运筹学排队论引言排队论是运筹学中的一个重要分支，它研究的是如何优化排队系统的设计和管理。
排队论广泛应用于各个领域，如交通流量控制、银行业务流程优化、生产线调度等，对于提高效率和降低成本具有重要意义。
本文将介绍排队论的基本概念、排队模型以及应用案例，帮助读者了解运筹学中排队论的基本原理和应用方法。
什么是排队论排队论是一门研究排队现象的数学理论，它通过定义排队系统的各个要素，如顾客到达率、服务率、队列容量等，建立数学模型分析和优化排队系统的性能指标。
排队论主要研究以下几个方面：•排队系统的模型：包括单服务器排队系统、多服务器排队系统、顾客数量有限的排队系统等。
•排队系统的性能指标：包括平均等待时间、系统繁忙率、系统容量利用率等。
•排队系统的优化方法：包括服务策略优化、系统容量规划等。
排队论的基本概念到达过程排队论中的到达过程是指顾客到达排队系统的时间间隔的随机过程。
常用的到达过程有泊松过程、指数分布等。
到达过程的特征决定了顾客到达的规律。
服务过程排队论中的服务过程是指服务器对顾客进行服务的时间间隔的随机过程。
常用的服务过程有指数分布、正态分布等。
服务过程的特征决定了服务的速度和效率。
排队模型排队模型是排队论中的数学模型，用于描述排队系统的性能和行为。
常用的排队模型有M/M/1模型、M/M/s模型等。
这些模型分别表示单服务器排队系统和多服务器排队系统。
性能指标排队系统的性能指标用于评估系统的性能，常见的性能指标有平均等待时间、系统繁忙率、系统容量利用率等。
这些指标可以帮助决策者优化排队系统的设计和管理。
排队模型与分析M/M/1模型M/M/1模型是排队理论中最简单的排队系统模型，它是一个单服务器、顾客到达过程和服务过程均为指数分布的排队系统。
M/M/1模型的性能指标可以通过排队论的公式计算得出。
M/M/s模型M/M/s模型是排队理论中的多服务器排队模型，它是一个多个服务器、顾客到达过程和服务过程均为指数分布的排队系统。
基于排队论的门诊服务队列研究中评价结果的优化分析
基于排队论的门诊服务队列研究中评价结果的优化分析目的通过评价了“基于排队论的门诊等待时间动态监测系统”所产生的监测数据，找到目前系统存在的问题，进一步研究改进方案。
方法采用比较分析的方法对门诊业务监测数据进行评价，并根据排队论计算模型的参数特征提出了新的优化方案。
结果经过对比分析与算法模型的理论研究，提供了新的算法改进方案。
结论应用排队论理论对门诊各环节服务水平进行评价与优化求解是可行的。
标签：排队论；排队过程模型；等待时间；优化求解；门诊服务Optimization Analysis of Evaluation Results of Outpatient Service Matched Cohort Analysis Based on the Queuing TheoryYAO Yue-peng，JI Xin-yu，WEI YunBeijing University of Chinese Medicine Dongfang Hospital Information Center，Beijing，100078 China[Abstract] Objective To find out the issues in the current system by evaluating the monitoring data of the outpatient waiting time dynamic monitoring system based on the queuing theory thus further researching the improvement plan. Methods The outpatient business monitoring data were evaluated by the comparative analysis method，and the new optimization plan was put forwards according to the parameter attribute of computer model of the queuing theory. Results The new algorithm improvement plan was put forwards after the comparative analysis and theoretical research of algorithm model. Conclusion It is feasible to evaluate the service levels of each link by using the queuing theory.[Key words] Queuing theory；Queuing process model；Waiting time；Optimization solution；Outpatient serrice作为医院信息管理部门，掌握着大量的门诊业务数据，为了更加有效地利用这些数据，为医院管理部门提供决策支持。
排队管理及相关战略研究综述
排队管理及相关战略研究综述引言排队管理是一种经济学上的重要领域，它涉及到资源分配、商品或服务供给、顾客满意度等多方面的问题。
在实际商业和服务场景中，排队现象屡见不鲜，如银行、医院、餐厅等各种场所常常需要顾客进行排队等候。
随着科技的不断发展和社会的不断进步，排队管理也变得越来越重要。
对排队管理及其相关战略的研究不仅可以为商家提供更好的服务，也能更好地满足顾客的需求，提升整个社会的运行效率。
本文将对排队管理及其相关战略进行综述，主要内容分为排队理论、排队系统的建模和优化、排队管理的策略和技术创新等方面。
通过对这些内容的综述，我们可以更好地了解排队管理的相关知识和应用，为相关领域的研究和实践提供参考和指导。
一、排队理论排队理论是研究排队现象的一门学科，它主要通过数学模型和统计方法来分析排队系统的运作机制，了解排队现象的规律和特点，为排队系统的优化提供理论指导。
排队理论主要涉及到平均等待时间、系统利用率、队列长度分布、排队模型等多个方面的内容。
平均等待时间是指在一个排队系统中，顾客平均等待的时间长度。
系统利用率是指排队系统中资源的利用率，它反映了资源的利用效率。
队列长度分布则描述了顾客在排队系统中等候的情况，它是排队理论中的一个重要指标。
排队模型是排队理论的核心内容，它利用概率论和统计学的方法对排队系统进行建模分析，以便更好地了解排队现象的本质。
二、排队系统的建模和优化在排队系统的建模方面，主要有单服务台排队模型、多服务台排队模型、无限排队模型等多种类型。
这些模型通过对排队系统中顾客到达和服务的规律进行建模，以便更好地了解排队系统的运作机制。
在排队系统的优化方面，主要有服务策略优化、资源配置优化、顾客流量控制等多个方面。
这些优化方法通过对排队系统的各个环节进行调整和优化，以提升排队系统的效率和服务质量。
三、排队管理的策略和技术创新排队管理的策略和技术创新是排队管理领域的一个重要发展方向，它主要通过引入新的技术和管理方法来提升排队系统的效率和服务质量。
DXC22-基于排队论的服务系统优化研究——以XX超市收银台为例
1、排队模型排队论是研究排队现象的理论与运用的学科，是专门研究由于随机因素的影响而产生的拥挤现象的科学，有人也称之为随机服务系统，或称之为公用事业的数学方法。
它是运筹学的一个重要的分支。
凡是出现拥挤现象的领域，都可以运用排队论。
在日常的生产和生活中有各种各样的随机服务系统，人们经常会碰到许多有形或无形的排队现象。
例如：到食堂打饭，到车站等车，去超市购物等等。
这些问题中，食堂的服务窗口与打饭者、公共汽车与乘客、超市收银台与购物者都可归结为服务窗口与顾客之间的一种服务关系，都可以当做排队问题来研究，他们之间就构成了一个排队系统或服务系统。
为了统一起见，我们把要求得到服务的对象统称为“顾客”，把提供服务的服务者称之为“服务员”、“服务窗口”、或“服务机构”。
因为顾客的到达情况和每位顾客接受服务的时间往往是无法事先知道的，或者说是随机的。
在排队论所研究的排队系统中，顾客相继到达时间间隔与服务时间这两个变量中至少有一个是随机的，因此排队论又称为随即服务系统理论。
排队系统的一般模型图如图1所示。
下图表明每个来到服务窗口的顾客需要按照排队规则进行排队等候服务，服务窗口则按照服务规则进行服务,顾客接受完服务之后就会离开。
图中的排队结构是指队列的数目和排队的方式，排队规则和服务规则说明顾客在排队系统中是按照什么规则，以什么次序接受服务的。
图1 排队系统一般模型图1）排队论的性态问题所谓排队系统的性态问题就是研究各种排队系统的规律性。
在一个排队系统中，其排队的队长是随机的，顾客等待时间的长短以及服务台繁忙时间的长短也是随机的。
排队系统的规律性主要是研究排队队长的分布、等待时间的分布以及忙期的分布，它包含了瞬间状态和统计平衡条件下的稳态两种情形。
2）排队系统的最优化问题排队系统的最优化问题主要有两类：包括系统的最优化设计和系统的最优化运行控制。
前者又称为静态最优化，后者又称为动态最优化。
前者是在服务系统设置之前就对未来的运行情况进行估计，从而使设计人员有所依据。
排队管理及相关战略研究综述
排队管理及相关战略研究综述排队管理是现代社会生活中不可或缺的一部分，它涉及到无数企业、机构、场所的顺利运作，是组织管理中不可缺少的一环。
排队问题的研究可以帮助人们改善生活、提高效率、提高服务质量，因此排队管理研究受到越来越多的关注。
排队模型是排队理论的基础，目的是研究排队系统的性质及其各种指标。
比较经典的排队模型有M/M/1模型、M/G/1模型、M/M/S模型等等。
对于排队模型，现代的排队管理理论研究主要涉及两个方面，一方面是如何优化队列模型，使其更好地反映现实环境中的问题，如修订排队模型，推导模型的各项指标等等；另一方面是针对队列模型的优化，确定能够达到最佳性能的排队策略，通过排队策略组织运作更好地实现产品与服务的生产和消费。
对于排队模型策略的优化，主要有几种经典的方法：变革队列模型和运营过程、优化队列模型的服务能力、改进排队策略和优化商业模式等等。
变革队列模型和运营过程通常通过引入新的技术、更新设备、增加服务人员等方式来改变排队环境，从而使排队模型更符合实际情况。
另外，优化队列模型的服务能力，通过增加服务站点、增加服务频次等方式来提高整个系统的服务能力。
改进排队策略则包括完善取号、分流、缓冲等方法，使整个队列过程更加合理化、高效化。
除此之外，对于连锁店、酒店、医院等组织，他们有着独特的服务特点以及对于队列模型的需求，因此他们需要依照自己的服务特点制定相应的排队策略。
如酒店优先安排会员入住，或医院提供预约服务等，这些措施都是为了提高顾客满意度和组织效益。
总之，排队管理的问题涉及到各个行业的管理者，能够为生产、服务和消费等各方面的问题提供优化方案和决策支持。
在今天的竞争环境中，经过优化后的排队方案能够有效的提高生产、服务、消费效率，并且能够满足人们对于高质量服务的要求。
因此，排队管理及其相关的战略研究是非常重要的，希望未来可以有更多相关的研究成果和实践案例。
基于博弈论的排队经济学模型及策略分析
基本内容
在建立排队系统的基础上，我们可以计算系统效率和客户服务质量。系统效 率是指排队系统在单位时间内处理客户或货物的数量，而服务质量则是指客户在 接受服务过程中的满意度。通过分析和优化排队系统，我们可以提高系统效率和 客户服务质量。
基本内容
为了提高系统效率和客户服务质量，我们需要对排队系统进行分析，并找出 其中的瓶颈和浪费现象。例如，如果客户服务时间过长，就会导致排队等待时间 增加，降低客户满意度；如果货物运输安排不合理，就会导致运输成本增加，影 响企业利润。针对这些问题，我们可以提出改进建议和优化措施。
基本内容
通过运用排队经济学模型和博弈论，我们可以制定出一种策略，即医院根据 历史数据预测病人到达时间和数量，并据此安排医生出诊时间。这种策略可以在 保证医院服务质量和效率的同时，最大限度地满足病人的需求。
基本内容
通过以上案例分析，我们可以看到排队经济学模型和博弈论在实践中的应用 效果显著。排队现象背后的经济学原理以及如何运用博弈论优化服务流程和人员 安排等问题具有重要的现实意义。在经济学、管理学等领域，排队经济学模型和 博弈论将继续发挥重要作用。
基本内容
在排队经济学模型中，顾客到达和服务流程是两个关键要素。顾客到达的方 式和时间会影响服务机构的排队现象和服务效率。服务流程包括服务时间、服务 窗口数量和服务人员数量等，这些因素都会对排队现象产生影响。通过博弈论， 我们可以进一步分析参与人（如顾客和服务机构）在给定条件下如何最优地选择 策略，以达到自身利益最大化。
基本内容
在未来的研究中，我们建议进一步拓展排队经济学模型的应用范围，将其应 用于更多领域的实际问题。可以结合其他理论或方法，如仿真模拟、优化算法等， 以更加深入地研究排队现象和博弈策略。此外，加强博弈论的普及教育，提高大 众对博弈论的认识和理解，也将有助于推广其在各个领域的应用。
基于排队论的公厕排队系统的分析与研究
基于排队论的公厕排队系统的分析与研究摘要：公共厕所入厕难已经成为我们社会的一个痼疾，尤其对于女性而言。
本文通过对数据的研究与分析，引出问题的实质，从而依据排队论的理论建立了问题的数学模型。
根据基本模型提出的假设应用MATLAP 给出了具体的实现过程及模型。
关键词：排队论；MATLAP；仿真系统一、引言均等并不总意味着公正。
这个悖论可以通过厕所前的排队长龙得到科学验证。
可别小看了这个问题，只需在公共场所略作观察就可发现，虽说男女洗手间的面积完全相等，但当男士们面不改色地在他们这边随进随出时，女洗手间外的长队却总是“尾大不掉”。
基于公共建筑物设计标准和男女各自生理特性作出的科学分析告诉我们，厕所外，女性的排队长度是男同胞的100多倍！通过分析国际上现有的相关资料，美国康奈尔大学的亚历山大·基拉（Alexander Kira）计算出两性小便时在厕所中的平均停留时间：男性为39 秒（±6 秒），女性为89 秒（±7 秒）。
女同胞的如厕时间平均为男子汉们的2.3 倍。
但这并不是导致排队差异的唯一原因，根据调查研究两列等待队伍的人数差异随厕位数量呈指数级增长。
为了研究此现象并找出适当的解决方案，设计了如下排队系统。
二、系统分析此现象可以用随机服务模型来描述，所以会应用到排队论的相关理论知识。
一般的随机排队系统有三个部分组成：人员到达规律，服务时间，排队规则。
对于公厕排队系统可以将这三部分做如下假设。
1.人员到达规律。
设在[t,t+△t]时间内到达一个人的概率与△t成正比，比例系数λ，到达两个及两个以上顾客的概率为o(△t)；在不相交的时间区内到达的人员数相互独立且人员无限。
根据概率论的基本知识，在上述假设下，在t时间到达的人员数服从泊松分布。
单位时间内到达人员的平均数是λ。
平均到达间隔为1/λ。
2.服务时间。
为了简化问题的复杂性，假设男女用厕时间都一定，且女士是男士的2.3 倍。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
基于排队论的决策系统研究【摘要】在排队系统中，顾客总是希望尽快接受服务，为减少顾客逗留时间（降低逗留费用），需要提高服务水平，服务水平是服务率μ和并行服务台数c 的函数，因此优化的目标是使两者的费用总和最小。
本文运用了排队系统“合适的”服务水平的决策模型：费用模型，渴望水平模型以及排队系统的经济分析等内容对上述问题进行了研究和分析，并用实例证明分析，以至于在服务水平和等待的各个冲突因素之间寻求某种平衡。
关键词：服务水平决策模型费用模型渴望水平模型一、前言1.1研究排队系统的必要性日常生活中我们常常需要等待服务，例如在参观就餐是等待服务，在超市付款台前“排队等候”，在邮局“排队”等待服务等。
但是排队现象也不仅仅是人类独有的，比如工件的等待机器加工，飞机在机场上空盘旋等待批准着陆，汽车等待交通信号灯等，它们也存在着排队现象。
排队现象花费极大的成本，等待现象是不可能完全消除的，我们的目标是把它不利影响减小到“可以忍受的”程度。
排队论主要是运用像：平均队列长度、平均等待时间，以及设施平均利用率这样的性能度量指标，来定量研究排队现象。
1.2 排队模型的要素一个排队系统中的主要参与之是顾客和服务台，顾客从某个输入源产生，到达一个服务设施，他们可以立即得到服务；加入服务设施繁忙，也可能在队列中等待。
当一个设施完成一次服务，如果有顾客等待的话，则自动地“拉出”一个等待顾客；加入队列为空，设施就变成空闲，直到新的顾客到达。
从分析队列的角度，我们用连续两个顾客之间的到达时间间隔来表示顾客的到达，用对每个顾客的服务时间来描述服务。
一般地，到达时间和服务时间可以是随机的，如邮局的服务系统；也可以是确定的，如求职面试申请者的到达。
队列长度对于队列的分析有作用，它可以是有限长的，如两个相邻机器之间的缓冲区；也可以是无限的，如邮寄订单处理。
排队规则表示从队列里选择顾客的顺序，是排队模型分析的一个重要因素。
最常见的排队规则是先到先服务（first come，first served，FCFS）。
其他的排队规则还有后到先服务（last come，first served，LCFS）和随机顺序服务（service in random order，SIRO）。
也可以按照某种优先权(priority)顺序从队列里挑选顾客，例如车间里把紧急工件放在普通工件前面进行处理。
在队列分析中，顾客的排队行为也起着重要作用。
“人类”顾客可能从一个队列跳到另一个队列，以期望缩短排队时间。
顾客也可能由于预计的排队时间过长而暂时不加入队列，或者可能会从一个队列中等待过久而退出，因为已经等待了太长的时间。
服务设施的设计可以包括并行服务，如邮局或银行服务，服务人员也可以安排成串行的，或者可以被连成网络。
产生顾客的输入源可以是有限的，也可以是无限的。
有限输入源限制等候服务的顾客，而无限输入源则始终是充分多的。
二、问题的提出与分析2.1 问题的提出一个排队系统中一般涉及到两类成本：服务机构的服务成本和顾客的等待成本。
服务机构的服务成本主要是建立服务机构、雇佣服务人员所需要支出的费用。
顾客等待成本是指顾客排队造成的损失，对赢利的服务系统而言，是指顾客因排队太长而离去，失去业务而造成的损失，对非赢利的服务机构而言是指顾客在队列中等待，浪费了时间，造成了社会损失。
在通常情况下，这两部分成本都与系统的服务水平有关，随着服务台数量的增加，服务成本增加，但顾客等待时间下降，等待成本减少。
因此，对于排队系统，需要解决如何确定一个服务水平使系统中上述两部分成本之和最小的优化问题。
图1反映了总成本、等待成本和服务成本三者之间的关系。
图 12.2 问题分析最优化问题的困难在于如何用单位时间的费用来衡量排队成本，以便能够和服务成本进行比较。
排队系统各种成本在稳态情形下，可以按单位时间来考虑。
一般情况下，单位时间的服务成本可以确切计算或估计，但顾客的等待成本就有不用的情况，如机器故障维修问题（顾客是等待维修的机器设备）等封闭性服务系统中的等待费用可以找到一定的数量关系，而对于开放性服务行业中顾客由于影响排队损失的因素很多，很难把顾客排队等待时间和成本费用以一种固定的关系联系起来，这样使得单位时间的等待成本难以确切计算，因此，往往需要采用统计等方法来加以估计。
（1）[M/M/1]模型中最优服务水平（μ∗）的确定对于[M/M/1]模型，提升服务员素质是改进服务质量的关键，这也意味着需要人力资源的投资（如培训等专项训练），因此，服务水平的提升也会使得服务成本的增加。
假设每提升一个单位的μ所需的成本为Cμ，一个顾客在排队系统中逗留一个单位时间所付出的等待成本为C w，L s为在系统中顾客平均数，T c为单位时间的总成本。
则有T c=C w×L s+μ×Cμ而L s=λμ−λ可见，T c是关于μ的函数，可求得使T c最小的μ∗为μ∗=λ+√λ×C wCμ据此计算得到的μ∗便是服务机构的最佳服务水平。
（2）、[M/M/C]模型中最优服务台数C∗的确定假设C w为一个顾客在排队系统中逗留一个单位时间所付出的成本；L s为在系统中的顾客平均数，C s为每个服务台单位时间的服务成本，C为服务台的数目，T c为单位时间的总成本，则有T c=C w×L s+C×C s如果将服务台数C看成是一个变量，则从L s的计算公式可知，L s是关于C的一个函数。
因此，单位时间成本T c也是关于服务台数C的一个函数，通过对T c求最小，可得到使单位时间成本最小的服务台数C∗的值，这便是[M/M/C]模型中的最优服务台数。
<1；首先，根据系统稳态要求，C必须满足λC×μ其次由于C不是连续变量，因此对T c求最小值不能使用微分方法。
假设C∗是最优服务台数，因此就有T c（C∗）≤T c（C∗−1）T c（C∗）≤T c（C∗+1）进一步的分析整理后得到≤L s(C∗−1)− L s(C∗)L s(C∗)−L s(C∗+1)≤C sC w再通过计算，可得到满足上述条件的最优服务台数C∗。
三、模型分析与案例说明基于排队系统的经济分析，可确定[M/M/1]模型中最优服务水平（μ∗）以及[M/M/C]模型中最优服务台数C∗，但提高服务水平会减少系统的等待时间的情况仍然存在，所以我们所要做的是在尽可能优的服务水平和服务台数的前提下，得出服务水平和等待时间的各个冲突因素之间的某种平衡。
首先引入费用模型概念和渴望水平模型概念。
3.1 费用模型费用模型试图平衡两种冲突的费用：（1）、提供服务的费用；（2）、在提供服务中延误时间（顾客等待时间）的费用。
这两种费用是相互冲突的，因为一个费用的增加，必然引起另一个费用的减少，如图1所示。
令x（=μ或c）表示服务水平，则费用模型可表示为ETC(x) =EOC(x) +EWC(x)其中ETC=单位时间的期望总费用EOC=单位时间运行设施的期望费用EWC=单位时间等待的期望费用EOC和EWC的最简单形式是下面的线性函数：EOC(x) =C1xEWC(x) =C2L s其中C1=没单位时间每单位x的边际成本C2=每一位(等待)顾客没单位时间的等待费用3.2渴望水平模型费用模型的适用性依赖于我们能否对费用参数做出很好的估计，一般情况下，这些参数是很难估计的，特别是与顾客等待时间有关的参数。
我们希望通过直接用排队系统性能度量指标的渴望水平模型来减轻这个困难。
这一模型思路是通过对冲突的性能度量指标设定一些合理的上限，来求出服务水平可以接受的范围，这些上限就是决策者想要达到的渴望水平。
在多服务台模型下，我们要确定某种“可以接受的”服务台数C∗，考虑下面两个（冲突的）度量指标：（1）、系统中的平均时间W s；（2）、服务台的空闲百分率X。
空闲百分率的计算如下：X=c−c̅c ×100=c−（L s−L q）c×100=(1−λeffcμ)×100[1]这个问题简化为求服务台数C∗，使得W s≤α，X≤β其中α和β为决策者制定的渴望水平，我们可以规定α=3分钟，β=10% 为了求解这个问题，可以画出W s和X作为c的函数的图像，如图2所示，在图像中找到а和β，我们可马上确定C∗的可接受范围，假如这两个条件不能同时满足，则在得出可行性范围之前，必须对其中一个范围或者两个范围都进行放松。
图2 用渴望水平模型进行排队决策3.3 案例说明基于上述两个模型，用下列案例来说明排队决策模型：在一家有多员工的工具库，交换工具的请求按照泊松分布发生，每小时平均有17.5个请求。
每个员工每小时平均能办理10个请求。
工具库雇用一名新员工的工资是每小时$12，每小时每台等待机床的生产损失成本约为$50.求该工具库最优员工数。
1、这个情形对应于（M/M/c）模型，其中需要求出c的最优值，因此，在本节开始给出的一般费用模型中，我们让x=c，得出下面的费用模型：ETC(c) = C1c+C2L s（c）=12c+50L s（c）L s（c）是该工具库（并列）员工数的函数。
我们用每小时λ=17.5个请求和每小时μ=10 个请求的（M/M/c）：（即对本例中的c≥2）时，该模（GD/∞/∞）模型。
在这种情况下，仅当c>λμ型达到平稳状态。
下表给出了求最优c值的计算结果，L s（c）的值表明，最优员工数应该为4。
2、假设我们需要确定员工人数，使得得到一个工具的期望等待时间不超过5分钟，同时，还要求空闲百分率低于20%。
在计算前我们可知，在得到工具前等待时间为5分钟的渴望上限是（即W s≤5分钟）不合理的。
因为根据问题的数据，平均服务时间本身就有6分钟。
下表给出了作为c的函数的W s和X值。
3、分析根据这些结果，我们应该减少服务时间，或者注意到该问题的背景中，工具的请求率高得不合理（λ=每小时17.5个请求），这很可能就是我们要解决的问题，例如我们可能需要分析一下工具替换率这么高的原因，是否工具设计本省有缺陷，或是因为机床操作工人的操作不当等干扰原因？四、总结在日常生活中排队等待现象是不可避免的，我们的目标是把排队等待的不利影响减小到“可以忍受的”程度。
一个排队系统中一般涉及到两类成本：服务机构的服务成本和顾客的等待成本。
在通常情况下，这两部分成本都与系统的服务水平有关，随着服务台数量的增加，服务成本增加，但顾客等待时间下降，等待成本减少。
在文章中，引用费用模型和渴望水平模型在服务水平和等待的各个冲突因素之间寻求某种平衡，并用案例证明了思想。
在案例中，通过套用模型的计算我们可得出合理的服务台数，并能通过计算值和理论值的对比分析发现现实中存在的一些问题。
五、参考文献[1]Hamdy A. Taha. [美] 薛毅，刘德刚，朱建明，侯思祥[译].运筹学导论初级篇人民邮电出版社[2]杜红. 应用运筹学. 浙江大学出版社[3]刘满凤，陶长琪，柳键.运筹学教程．清华大学出版社。