第7章 图论7树与生成树PPT课件
合集下载
7-7 树与生成树

定理7.2 任一棵树至少有两片树叶。 证明 设树T=〈V,E〉,|V|=v, 则deg(vi)=2(v-1) 因为T是连通图,对于任意viT, 有deg(vi)≥1 若T中每一个结点的度数大于等于2, 则deg(vi) ≥2v,得出矛盾。 若T中只有一个结点度数为1,其它结点的度数 大于等于2,则 deg(vi) ≥2(v-1)+1=2v-1,得出矛盾。 故T至少有两个结点度数为1。
下面我们讨论带权的生成树。 设图G中的一个结点表示一些城市,各 边表示城市间道路的连接情况,边的权表 示道路的长度,如果我们要用通讯线路把 这些城市连接起来,要求沿道路架设线路 时,所用的线路最短,这就是要求一棵生 成树,使该生成树是图G的所有生成树中 边权的和为最小。
现在讨论一般带权图的情况。 假定图G是具有n个结点的连通图。对应于 G的每一条边e,指定一个正数C(e),把 C(e)称作边e的权,(可以是长度、运输 量、费用等)。G的生成树也具有一个 树权C(T),它是T的所有边权的和。 定义7.3 最小生成树 在带权的图G的所有生成树中,树权最小 的那棵生成树,称作最小生成树。
定理7.4 一条回路和任意一棵生成树的补 至少有一条公共边。 证明 若有一条回路和一棵生成树的补没有 公共边,那么这回路包含在生成树之中, 然而这是不可能的,因为一棵生成树不 能包含回路。
定理7.5 一个边割集和任何生成树至少有 一条公共边。 证明 若有一条边割集和一棵生成树没有公 共边,那么删去这个边割集后,所得的 子图必然包含该生成树,这意味着删去 边割集后仍然连通,与边割集定义矛盾。
图7.5 带权的图
例如图7.5(a)中给出一个带权连通图。粗线 表示按上述算法得到的最小生成树。 以上算法假设G中边权不相同,实际上, 这种算法完全适用于任意边权的情况, 若有两条边的权相同,我们可以用其中 一条边的权改变一个很小的量,因为G 中的边是有限的,总可选择这个改变量 而不影响最小生成树的最小性。 图7.5(b)中的粗线表示了最小生成树。
树与生成树全解
定理7-7.4 一条回路和任意一棵生成树的 补至少有一条公共边。 证明 若有一条回路和一棵生成树的补没有 公共边,那么这回路包含在生成树之中, 然而这是不可能的,因为一棵生成树不 能包含回路。
定理7-7.5 一个边割集和任何生成树至少 有一条公共边。 证明 若有一条边割集和一棵生成树没有公 共边,那么删去这个边割集后,所得的 子图必然包含该生成树,这意味着删去 边割集后仍然连通,与边割集定义矛盾。
定理7-7.2 任一棵树至少有两片树叶。 证明 设树T=〈V,E〉,|V|=v, 则deg(vi)=2(v-1) 因为T是连通图,对于任意viT, 有deg(vi)≥1 若T中每一个结点的度数大于等于2, 则deg(vi) ≥2v,得出矛盾。 若T中只有一个结点度数为1,其它结点的度数 大于等于2,则 deg(vi) ≥2(v-1)+1=2v-1,得出矛盾。 故T至少有两个结点度数为1。
7-7 树与生成树
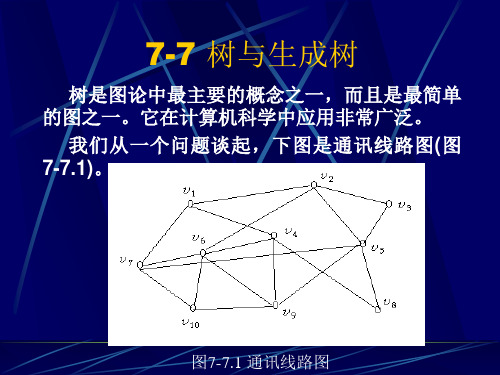
树是图论中最主要的概念之一,而且是最简单 的图之一。它在计算机科学中应用非常广泛。 我们从一个问题谈起,下图是通讯线路图 ( 图 7-7.1)。
图7-7.1 通讯线路图
其中 v1 , v2,…,v10 是十个城市,线路只 能在这里相接。不难发现,只要破坏了几 条线路,立即使这个通讯系统分解成不相 连的两部分。但要问在什么情况下这十个 城市依然保持相通?不难知道,至少要有 九条线把这十个城市连接在一起,显然这 九条线是不存在任何回路的,因而九条线 少一条就会使系统失去连通性。
⑶⑷ 若T连通且有v-1条边。 当v=2时,e=v-1=1,故T必无回路。如增加一条边得 到且仅得到一个回路。 设v=k-1时命题成立。 考察v=k时的情况,因为T是连通的,e=v-1。故每个 结点 u有deg(u)≥1 ,可以证明至少有一结点 u0 ,使 deg(u0)=1,若不然,即所有结点 u有 deg(u) ≥2, 则2e≥2v,即e≥v与假设e=v-1矛盾。删去u0及其关 联的边,而得到图T’,由归纳假设得知T’无回路, 在T’中加入u0及其关联边又得到T,故T无回路的, 如在 T中增加一条边 (ui ,uj) ,则该边与 T中 ui到 uj的 路构成一个回路,则该回路必是唯一的,否则若删 除这条新边,T必有回路,得出矛盾。
离散数学7-树

(b)
(a)
V5
2
1
V7
8
9
V2
V4
2
3
V8
5
V1
V1
V4
V5
1
3
V7
V6
8
V4
2
V8
5
6
V1
1
V5
6
V7
V6
8
3
V8
5
6
V7
9
V3
(e)
V3
(f)
(g)
22
V2
V3
(h)
五.应用举例——求最小生成树
例3 用管梅谷算法求下图的最小生成树。
23
五.应用举例——求最小生成树
例3 用管梅谷算法求下图的最小生成树。
成圈。
首先证明T无简单回路。对n作归纳证明。
(i) n=1时,m=n-1=0,显然无简单回路;
(ii)假设顶点数为n-1时无简单回路,现考察顶点数是n的情况:此时至少有一
个顶点v其次数d(v)=1。因为若n个顶点的次数都大于等于2,则不少于n条边,但这与
m=n-1矛盾。
删去v及其关联边得到新图T’,根据归纳假设T’无简单回路,再加回v及其关联
边又得到图T,则T也无简单回路。
再由图的连通性可知,加入任何一边后就会形成圈,且只有一个圈,否则原图
中会含圈。
9
二. 基本定理——证明
证明(4):(3)(4),即证一个无圈图若加入任一边就形成圈,
则该图连通,且其任何一边都是桥。
若图不连通,则存在两个顶点vi和vj,在vi和vj之间没有路,若
加边(vi,vj)不会产生简单回路,但这与假设矛盾。由于T无简单回
第七章 图论

i1
本讲稿第十三页,共九十一页
§7.1 图的基本概念
例:若图G有n个顶点,(n+1)条边,则G中至少 有一个结点的度数≥3。
证明:设G中有n个结点分别为v1,v2,…,vn,则由握手
定理:
n
degvi)(2e2(n1)
i1
而结点的平均度数=
2(n1)212
n
n
∴结点中至少有一个顶点的度数≥3
本讲稿第十四页,共九十一页
▪ 若G’ G,且G’ ≠G(即V’V或E’ E),则称G’是G的真子图;
▪ 若V’=V,E’E,则称G’是G的生成子图(支 撑子图)。
本讲稿第二十三页,共九十一页
§7.1 图的基本概念
2.子图和图的同构:
例:G图如下:G的真子图:
生成子图:
说明: (1)G也是G的生成子图; (2)G’=〈V,〉也是G的生成子图。
(3)路径长度:若两个结点之间有一条路经P,则路 径|P|=P中边的条数。 例:给出有向图G,求起始于1,终止于3的路径
本讲稿第三十二页,共九十一页
§7.2 路与回路
下面介绍一些专有名词:
(1)穿程全部结点的路径:经过图中所有结点的路径。 (2)简单路径:在有向图中经过边一次且仅一次的路径。
(3)基本路径:在)从一个结点到某一结点的路径,(若有的话)不 一定是唯一的; (2)路径的表示方法:
(a)边的序列表示法: 设G=<V,E>为一有向图, ,则路径可以表示
成:(<v1,v2>,<v2,v3>,….<vk-1,vk>)vi V
本讲稿第三十一页,共九十一页
§7.2 路与回路
(b)结点序列表示法: (v1,v2vk)
本讲稿第十三页,共九十一页
§7.1 图的基本概念
例:若图G有n个顶点,(n+1)条边,则G中至少 有一个结点的度数≥3。
证明:设G中有n个结点分别为v1,v2,…,vn,则由握手
定理:
n
degvi)(2e2(n1)
i1
而结点的平均度数=
2(n1)212
n
n
∴结点中至少有一个顶点的度数≥3
本讲稿第十四页,共九十一页
▪ 若G’ G,且G’ ≠G(即V’V或E’ E),则称G’是G的真子图;
▪ 若V’=V,E’E,则称G’是G的生成子图(支 撑子图)。
本讲稿第二十三页,共九十一页
§7.1 图的基本概念
2.子图和图的同构:
例:G图如下:G的真子图:
生成子图:
说明: (1)G也是G的生成子图; (2)G’=〈V,〉也是G的生成子图。
(3)路径长度:若两个结点之间有一条路经P,则路 径|P|=P中边的条数。 例:给出有向图G,求起始于1,终止于3的路径
本讲稿第三十二页,共九十一页
§7.2 路与回路
下面介绍一些专有名词:
(1)穿程全部结点的路径:经过图中所有结点的路径。 (2)简单路径:在有向图中经过边一次且仅一次的路径。
(3)基本路径:在)从一个结点到某一结点的路径,(若有的话)不 一定是唯一的; (2)路径的表示方法:
(a)边的序列表示法: 设G=<V,E>为一有向图, ,则路径可以表示
成:(<v1,v2>,<v2,v3>,….<vk-1,vk>)vi V
本讲稿第三十一页,共九十一页
§7.2 路与回路
(b)结点序列表示法: (v1,v2vk)
图论的介绍ppt课件

chedules
工程项目的任务安排,如何满足限制条件,并在最短时 间内完成?
Program structure
大型软件系统,函数(模块)之间调用关系。编译器分 析调用关系图确定如何最好分配资源才能使程序更有效 率。
Graph Applications
Graph Problems and Algorithms
图论的介绍ppt课件
欧拉路径 解決哥尼斯保七桥问題
原來是一笔画问题啊!
数学家欧拉(Euler, 1707-1783) 于1736年严格的证明了上述哥尼斯堡 七桥问题无解,并且由此开创了图论的典型思维方式及论证方式
实际生活中的图论 Graph Model
电路模拟
例:Pspice、Cadence、ADS…..
哈密頓(Hamilton) 周遊世界问題
正十二面体有二十个顶点 表示世界上20个城市 各经每个城市一次 最后返回原地
投影至平面
哈密頓路径至今尚无有效方法來解決!
最短路径问題
(Shortest Path Problem)
最快的routing
最快航線
B 2
1
E
3
A
C 1
3 2F
1
3
D
3 3
G
最短路径算法Dijkstra算 法
二分图(偶图) Bipartite graphs
A graph that can be decomposed into two partite sets but not fewer is bipartite
It is a complete bipartite if its vertices can be divided into two non-empty groups, A and B. Each vertex in A is connected to B, and viceversa
工程项目的任务安排,如何满足限制条件,并在最短时 间内完成?
Program structure
大型软件系统,函数(模块)之间调用关系。编译器分 析调用关系图确定如何最好分配资源才能使程序更有效 率。
Graph Applications
Graph Problems and Algorithms
图论的介绍ppt课件
欧拉路径 解決哥尼斯保七桥问題
原來是一笔画问题啊!
数学家欧拉(Euler, 1707-1783) 于1736年严格的证明了上述哥尼斯堡 七桥问题无解,并且由此开创了图论的典型思维方式及论证方式
实际生活中的图论 Graph Model
电路模拟
例:Pspice、Cadence、ADS…..
哈密頓(Hamilton) 周遊世界问題
正十二面体有二十个顶点 表示世界上20个城市 各经每个城市一次 最后返回原地
投影至平面
哈密頓路径至今尚无有效方法來解決!
最短路径问題
(Shortest Path Problem)
最快的routing
最快航線
B 2
1
E
3
A
C 1
3 2F
1
3
D
3 3
G
最短路径算法Dijkstra算 法
二分图(偶图) Bipartite graphs
A graph that can be decomposed into two partite sets but not fewer is bipartite
It is a complete bipartite if its vertices can be divided into two non-empty groups, A and B. Each vertex in A is connected to B, and viceversa
7-7 树与生成树

实例
例 设G为n(n≥5)阶简单图,证明 或G的补图中必含 为 ( )阶简单图,证明G或 的补图中必含 圈。 设简单图G和其补图的边数分别为 和其补图的边数分别为m和 , 证 设简单图 和其补图的边数分别为 和m’,则 m+m’= n(n-1)/2 根据鸽巢原理, 与其补图必有一个边数 与其补图必有一个边数≥ 根据鸽巢原理,G与其补图必有一个边数 n(n-1)/4 , 不妨设G的边数 下面证G中必含有圈 中必含有圈。 不妨设 的边数m≥ n(n-1)/4 ,下面证 中必含有圈。 的边数 假设G中没有圈, 个连通分支, 假设 中没有圈,设G有w个连通分支,则每个连通分支 中没有圈 有 个连通分支 都是树, 分别为第i个连通分支 都是树,mi=ni-1,i=1,…,w,mi,ni分别为第 个连通分支 , , 的边数与阶数, 的边数与阶数,所以有
实例
下面两个正整数序列中, 例 下面两个正整数序列中,哪个能充当无向树的度 数序列?若能画出2棵非同构的无向树 棵非同构的无向树。 数序列?若能画出 棵非同构的无向树。 (1)1,1,1,1,2,3,3,4 ) (2)1,1,1,1,2,2,3,3 ) 解 (1)不可以,因为所有度数之和等于 ,而结点 )不可以,因为所有度数之和等于16, 数为8,假设可以构成树,则度数之和应为14, 数为 ,假设可以构成树,则度数之和应为 ,所 以不可以。 以不可以。 (2)可以。 )可以。
Go
(1)⇒(2)的证明 ⇒ 的证明
如果T是无回路的连通图, 中无回路且e=v− , 如果 是无回路的连通图,则G中无回路且 −1,其 中无回路且 是边数, 中e是边数,v是结点数 是边数 是结点数 归纳法。 证明 归纳法。 当v=2时,因为 连通无回路, 连通无回路, 时 因为T连通无回路 所以只有e=1,故e=v-1成立。 , 成立。 所以只有 成立 假设v=k-1时命题成立,当v=k时, 时命题成立, 假设 时命题成立 时 是无回路且连通, 的结点u, 因T是无回路且连通,则至少有一个度为 的结点 , 是无回路且连通 则至少有一个度为1的结点 设与其关联的边为(u,w),删去u,得到一个 个结点 ,删去 ,得到一个k-1个结点 设与其关联的边为 的连通无向图T’, 的连通无向图 ,
图论课件--最小生成树共37页
1、最灵繁的人也看不见自己的背脊。——非洲 2、最困难的事情就是认识自己。——希腊 3、有勇气承担命运这才是英雄好汉。——黑塞 4、与肝胆人共事,无字句处读书。——周恩来 5、阅读使人充实,会谈使人敏捷,写作使人精确。——培根
图论课件--最小生成树
1、纪律是管理关系的形式。——阿法 纳西耶 夫 2、改革如果不讲纪律,就难以成功。
3、道德行为训练,不是通过语言影响 ,而是 让儿童 练习良 好道德 行为, 克服懒 惰、轻 率、不 守纪律 、颓废 等不良 行为。 4、学校没有纪律便如磨房里没有水。 ——夸 美纽斯
5、教导儿童服从真理、服从集体,养 成儿童 自觉的 纪律性 ,这是 儿童道 德教育 最重要 的部分 。—— 陈鹤琴
第7章 图论7树与生成树PPT课件
图 7.6.5
写在最后
经常不断地学习,你就什么都知道。你知道得越多,你就越有力量 Study Constantly, And You Will Know Everything. The More
You Know, The More Powerful You Will Be
23
谢谢大家
荣幸这一路,与你同行
如要建造一个连接若干城市的铁路网络已知城市v之间直达铁路的造价设计一个总造价为最小的铁路网络就是求最小生成树t的克鲁斯克尔kruskal算法
7.6 树与生成树
7.6.1 无向树 7.6.2无向图中的生成树与最小生成树
7.6.1 无向树
树是图论中的一个重要概念。早在1847年 克希霍夫就用树的理论来研究电网络, 1857年 凯莱在计算有机化学中C2H2n+2的同分异构物 数目时也用到了树的理论。 而树在计算机科学 中应用更为广泛。本节介绍树的基本知识, 其 中谈到的图都假定是简单图。
其次,若在连通图T中增加一条新边(vi, vj ),则由于T中由vi到 vj存在一条通路,故必有一个圈通过vi, vj 。若这样的圈有两 个,则去掉(vi, vj ), T中必存在通过vi, vj的圈,与T无圈矛盾。 故加上边(vi, vj )得到一个切仅一个圈。
(4)证明由第(4)条可推出第(5)条。
【例7.6.1】判断图 7.6.2中各图是否为树. 图 7.6.2
定理7.6.1 T是一个无向图(n, m)图, 则以下关于T的 命题是等价的: (1)T是树。 (2)T无圈且m=n-1。 (3) T连通且m=n-1。 (4)T无圈,但增加任一新边,得到且仅得到一个圈。 (5)T连通,但删去任一边便不连通(n≥2)。 (6)T的每一对结点间有唯一的一条通路。(n≥2)。
写在最后
经常不断地学习,你就什么都知道。你知道得越多,你就越有力量 Study Constantly, And You Will Know Everything. The More
You Know, The More Powerful You Will Be
23
谢谢大家
荣幸这一路,与你同行
如要建造一个连接若干城市的铁路网络已知城市v之间直达铁路的造价设计一个总造价为最小的铁路网络就是求最小生成树t的克鲁斯克尔kruskal算法
7.6 树与生成树
7.6.1 无向树 7.6.2无向图中的生成树与最小生成树
7.6.1 无向树
树是图论中的一个重要概念。早在1847年 克希霍夫就用树的理论来研究电网络, 1857年 凯莱在计算有机化学中C2H2n+2的同分异构物 数目时也用到了树的理论。 而树在计算机科学 中应用更为广泛。本节介绍树的基本知识, 其 中谈到的图都假定是简单图。
其次,若在连通图T中增加一条新边(vi, vj ),则由于T中由vi到 vj存在一条通路,故必有一个圈通过vi, vj 。若这样的圈有两 个,则去掉(vi, vj ), T中必存在通过vi, vj的圈,与T无圈矛盾。 故加上边(vi, vj )得到一个切仅一个圈。
(4)证明由第(4)条可推出第(5)条。
【例7.6.1】判断图 7.6.2中各图是否为树. 图 7.6.2
定理7.6.1 T是一个无向图(n, m)图, 则以下关于T的 命题是等价的: (1)T是树。 (2)T无圈且m=n-1。 (3) T连通且m=n-1。 (4)T无圈,但增加任一新边,得到且仅得到一个圈。 (5)T连通,但删去任一边便不连通(n≥2)。 (6)T的每一对结点间有唯一的一条通路。(n≥2)。
7-7树与生成树
的边是e1,e2,…,en-1 。根据构造, T0没有圈,由定理7-7.1可知T0是 一棵树,且为图G的生成树。
下面证明T0是最小生成树。 设 T 是图 G 的一棵最小生成树,若 T 与 T0 相同,则 T0 是 G 的最小生成树。 若 T 与 T0 不同,则在 T0 中至少有一条边 ei+1 ,使得 ei+1 不是 T 的边,但 e1 , e2,…,ei 是T的边。因为T是树,我们在T中加上边ei+1 ,必有一条圈r, 而T0是树,所以r中必存在某条边 f不在T0中。对于树T,若以边ei+1置换f, 则得到新的一棵树 T’,但树T’的权 C(T’)=C(T)+C(ei+1 )- C(f)。因为 T是最 小生成树,故C(T)≤C(T’)即
三、最小生成树
1、最小生成树定义
设图G=<V,E,W>是赋权连通简单图,其 中每一边的权W(i,j)是非负实数。生成树T的权 定义为W(T)= 树T中所有的边权之和。使W(T)具 有最小值的生成树称为G的最小生成树。
2、最小生成树求法----kruskal算法。
定理 7-7. 6 ( Kruskal) 产生的是最小生成树。 设 连通图 G 有 n 个结点,以下算法
(4) 4=>5 即无圈,但增加任一新边,得到且
仅得到一个圈=>连通,但删去任一边,图便
不连通。(n>=2) 证:(a)证明图是连通的(用反证法)。 若图不连通,则存在vi,vj,使vi,vj之间没有 路。显然增加边<vi,vj>不产生圈,与前提矛 盾。 (b)因T无圈,故删去任一边,图便不连通 (为?)。
(3)3=>4 即T连通且e=v-1的图=>无圈,但增加任一条新边,
下面证明T0是最小生成树。 设 T 是图 G 的一棵最小生成树,若 T 与 T0 相同,则 T0 是 G 的最小生成树。 若 T 与 T0 不同,则在 T0 中至少有一条边 ei+1 ,使得 ei+1 不是 T 的边,但 e1 , e2,…,ei 是T的边。因为T是树,我们在T中加上边ei+1 ,必有一条圈r, 而T0是树,所以r中必存在某条边 f不在T0中。对于树T,若以边ei+1置换f, 则得到新的一棵树 T’,但树T’的权 C(T’)=C(T)+C(ei+1 )- C(f)。因为 T是最 小生成树,故C(T)≤C(T’)即
三、最小生成树
1、最小生成树定义
设图G=<V,E,W>是赋权连通简单图,其 中每一边的权W(i,j)是非负实数。生成树T的权 定义为W(T)= 树T中所有的边权之和。使W(T)具 有最小值的生成树称为G的最小生成树。
2、最小生成树求法----kruskal算法。
定理 7-7. 6 ( Kruskal) 产生的是最小生成树。 设 连通图 G 有 n 个结点,以下算法
(4) 4=>5 即无圈,但增加任一新边,得到且
仅得到一个圈=>连通,但删去任一边,图便
不连通。(n>=2) 证:(a)证明图是连通的(用反证法)。 若图不连通,则存在vi,vj,使vi,vj之间没有 路。显然增加边<vi,vj>不产生圈,与前提矛 盾。 (b)因T无圈,故删去任一边,图便不连通 (为?)。
(3)3=>4 即T连通且e=v-1的图=>无圈,但增加任一条新边,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(2)证明由第(2)条可推出第(3)条。
用反证法。若图不连通,设T有k个连通分支 (k≥2)T1,T2,…,Tk,其结点数分别是n1,n2,…,nk,边数分别为 m1,m2,…,mk,
于是
k
k
ni n,mi m
i1
i1
k
k
mm i (ni1)nkn1
i1
i1
得出矛盾。所以T是连通且m=n-1的图。
所以x=9,即树T有9片树叶。
7.6.2无向图中的生成树与最小生成树
定义7.6.2 若无向(连通图)G的生成子图是一棵 树,则称该树是G的生成树,记为TG。生成树 TG中的边称为树枝。图G中其它边称为TG的弦。 所有这些弦的集合称为TG的补。
如 图 7.6.3 中 (b) 、 (c) 所 示 的 树 T1 、 T2 是 (a) 图的生成树,而(d)所示的树T3不是(a)图的生成 树。一般的,图的生成树不唯一。
考虑生成树T1,可知e1,e2,e3,e4是T1的树枝, e5,e6,e7是T1的弦,集合{e5,e6,e7}是T1的 补。生成树有其一定的实际意义。
图 7.6.3
【例7.6.3】某地要兴建5个工厂,拟修筑道路连接 这5处。经勘测其道路可依如图7.6.3(a)图的无向边 铺设。为使这5处都有道路相通,问至少要铺几条 路?
7.6 树与生成树
7.6.1 无向树 7.6.2无向图中的生成树与最小生成树
7.6.1 无向树
树是图论中的一个重要概念。早在1847年 克希霍夫就用树的理论来研究电网络, 1857年 凯莱在计算有机化学中C2H2n+2的同分异构物 数目时也用到了树的理论。 而树在计算机科学 中应用更为广泛。本节介绍树的基本知识, 其 中谈到的图都假定是简单图。
定义7.6.1 一个连通无圈无向图称为无向树(简 称为树)。记作T。树中度数为1的结点称为树叶 (或终端结点), 度数大于1的结点称为分枝点 (或内点,或非终端结点)。一个无圈图称为森 林。
显然若图G是森林,则G的每个连通分支是 树。如图7.6.1(a)所示的是一棵树;(b)所示的是森 林。
图 7.6.1 树和森林示意图
(3)证明由第(3)条可推出第(4)条。
首先证明T无圈。对n作归纳证明。
n=1时,m=n-1=0,显然无圈。
假设结点数为n-1时无圈,今考察结点数是n的情况。此 时至少有一个结点v其度数deg(v)=1。我们删去v及其关联边 得到新图T′,根据归纳假设T′无圈,再加回v及其关联边又得 到图T,则T也无圈。
若图不连通,则存在两个结点vi和vj,在vi和vj之间没有路, 若加边(vi,vj)不会产生简单回路(圈),但这与假设矛盾。 由于T无圈,所以删去任一边,图便不连通。
(5) 证明由第(5)条可推出第(6)条。
由连通性知,任两点间有一条路径,于是有一条通路。 若此通路不唯一,则T中含有简单回路,删去此回路上任一 边,图仍连通,这与假设不符,所以通路是唯一的。
解 这实际上是求G的生成树的边数问题。
一般情况下,设连通图G有n个结点,m条边。 由树的性质知,T有n个结点,n-1条树枝, m- n+1条弦。
在图7.6.3(a)中,n=5,则n-1=5-1=4, 所以至少要修4条路才行。
定义7.6.3 设G=〈V , E〉是一连通的有权图,则 G的生成树TG为带权生成树, TG的树枝所带权之和称 为生成树TG的权,记为W(TG ) 。G中具有最小权的生 成树TG称为G的最小生成树。
【例7.6.1】判断图 7.6.2中各图是否为树. 图 7.6.2
定理7.6.1 T是一个无向图(n, m)图, 则以下关于T的 命题是等价的: (1)T是树。 (2)T无圈且m=n-1。 (3) T连通且m=n-1。 (4)T无圈,但增加任一新边,得到且仅得到一个圈。 (5)T连通,但删去任一边便不连通(n≥2)。 (6)T的每一对结点间有唯一的一条通路。(n≥2)。
求最小生成树问题是有实际意义的。
如要建造一个连接若干城市的铁路网络,已知 城市vi和vj之间直达铁路的造价,设计一个总造价为 最小的铁路网络,就是求最小生成树TG。
其次,若在连通图T中增加一条新边(vi, vj ),则由于T中由vi到 vj存在一条通路,故必有一个圈通过vi, vj 。若这样的圈有两 个,则去掉(vi, vj ), T中必存在通过vi, vj的圈,与T无圈矛盾。 故加上边(vi, vj )得到一个切仅一个圈。
(4)证明由第(4)条可推出第(5)条。
n
deg(i)2(n1)2n2
(3)
i1
(2),(3)都与(1)矛盾。所以T中至少有两片树叶。
【例7.6.2】T是一棵树,有两个2度结点,一个3度结点,三个
4度结点,T有几片树叶?
解: 设树T有x片树叶,则T的结点数
n=2+1+3+x
T的边数
m=n-1=5+x
又由
n
2m deg(vi )
i1
得
2 ·(5+x)=2·2+3·1+4·3+x
定理7.6.2 任一树T中,至少有两片树叶(n≥2时)。 证:因为T是一棵n≥2的(n, m)树, 所以由 定理7.4.1, 有
n
deg(i)2m2(n1)2n2 (1)
i1
若T中的无树叶, 则T中每个顶点的度数≥2,则
Σdeg(vi)≥2n,
(2)
若T中只有一片树叶,则T中只有一个结点度数为1, 其它结点度数≥2, 所以
证:(1)证明由树的定义可知T无圈。下证m=n-1。
对n作归纳。 n=1时,m=0,显然m=n-1。
假设n=k时命题成立,现证明n=k+1时也成立。 由于树是连通而无圈,所以至少有一个度数为1的结 点v,在T中删去v及其关联边,便得到k个结点的连通无圈 图。由归纳假设它有k-1条边。再将顶点v及其关联边 加回得到原图T,所以T中含有k+1个顶点和k条边,符合 公式m=n-1。 所以树是无圈且m=n-1的图。
(6) 证明由第(6)条可推出树的定义。
显然连通。若有圈,则圈上任意两点间有两条通路, 此与通路的唯一性矛盾。证毕。
由定理7.5.2所刻画的树的特征可见: 在结点数给 定的所有图中, 树是边数最少的连通图, 也是边数 最多的无圈图。 由此可知, 在一个(n, m)图G有圈。
