医药数理统计方法教学大纲
《医药统计分析》课程教学大纲
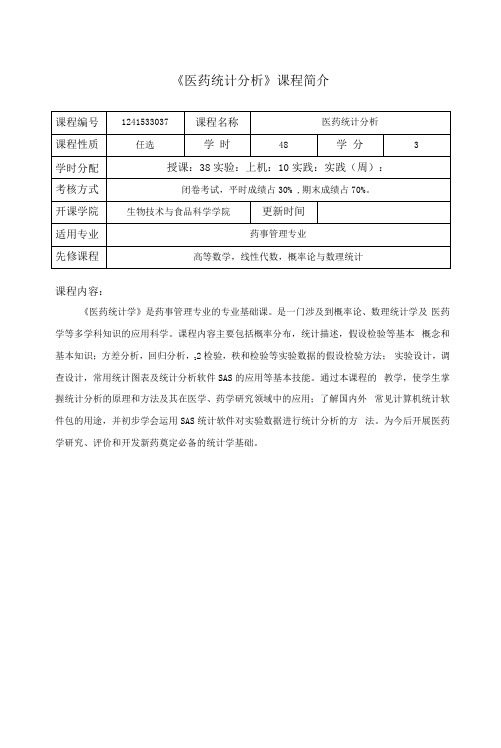
《医药统计分析》课程简介课程内容:《医药统计学》是药事管理专业的专业基础课。
是一门涉及到概率论、数理统计学及医药学等多学科知识的应用科学。
课程内容主要包括概率分布,统计描述,假设检验等基本概念和2检验,秩和检验等实验数据的假设检验方法;实验设计,调基本知识;方差分析,回归分析,Z查设计,常用统计图表及统计分析软件SAS的应用等基本技能。
通过本课程的教学,使学生掌握统计分析的原理和方法及其在医学、药学研究领域中的应用;了解国内外常见计算机统计软件包的用途,并初步学会运用SAS统计软件对实验数据进行统计分析的方法。
为今后开展医药学研究、评价和开发新药奠定必备的统计学基础。
2.多元线性回归分析教学重点、难点:线性回归分析的SAS程序中数据步和过程步的格式、语句及输出结果的分析。
二、教学基本要求上机一t检验与方差分析教学要求:掌握应用SAS统计软件进行t检验和单因素方差分析的方法及对其输出结果的分析。
上机二双检验与秩转换的非参数检验教学要求:掌握应用SAS统计软件进行N检验与秩转换的非参数检验的方法及对其输出结果的分析。
上机三回归分析教学要求:掌握一元线性及多元线性回归分析的SAS程序及输出结果的分析方法。
三、章节学时分配四、教材与主要参考资料教材[1]上机指导(自编)参考资料[1]何雁,马志庆.医药数理统计(第3版).北京:科学出版社,2009.[2]倪宗瓒.卫生统计学(第四版).北京:人民卫生出版社,2001.[3]贺佳,医学统计学中的SAS统计分析.上海:第二军医大学出版社,2002.Brief IntroductionMedical and Pharmaceutical statistics is one of the basic courses of Pharmacy Administration Program. It is an applied science related to probability theory, statistics, medicine, pharmacy, and so on. The main parts of this course are probability distribution, statistical description, and hypothesis test (such as analysis of variance, regression analysis, chi-square test, and rank sum test); experiment design, survey design, application of statistical graph, statistical table, and statistical analysis system (SAS). The students will grasp the principle and method of statistical analysis and its application in the field of medicine and pharmacy research, as well as learn about the usage of statistical package and experiment data process method by SAS. It is a statistics foundation for drug research, evaluation and new drug research.《医药统计分析》课程教学大纲一、教学内容第一章绪论1.1统计与医药统计学1.2变量与数据类型1.3统计学的假设干概念1.4医、药学研究的统计过程1.5如何学习医药统计学教学重点、难点:变量与数据类型。
医用数理统计方法课件第一章

B
A
A={2,4} B={1,5,6}
(一)事件的关系和运算
7.互逆关系: 若事件A与事件B互斥,且在任何一次试验中二者必定有一个发生,即A∩ B =Ø且A+B=Ω,则称事件A与事件B互逆(或相互对立)。称事件A为事件的B的对立事件, 记为 或 A与B没有相同的样本点 A或B的样本点组成样本空间 推广:完备事件组
就一次试验而言,试验结果没有规律,但“大数次”地重复这个试验,试验结果又遵循某些规律,这种规律称之为“统计规律”
如掷硬币(下表) 概率论与数理统计就是研究随机现象的统计规律的数学学科
统计规律
05
04
02
03
01
试验者 试验次数 正面出现次数 频率
德摩根 2048 1039 0.5073
第三次数学危机
数学家罗素关于集合论的悖论: 设A是以一切自己不属于自己的那种集合为元素构成的集合,即若B B,则B ∈ A; 若B ∈B, 则B A。 问:A属于自己吗? 若A ∈A,由定义A A 若A A,由定义A ∈ A
罗素悖论的出现引起集合论的矛盾 被称为数学上的第三次危机
第三次数学危机:集合论-悖论
1
某人:“我说的这句话是谎话。”
2
这句话是真话还是谎话? 理发师:“我只给那些不给自己刮胡子的人刮胡子。”
理发师能否给自己刮胡子?
4
解决方法
公理化
6
有一类特殊的试验,它具有下面两个特征: 试验中的所有可能结果(即基本事件)只有有限个,而且是两两互斥的; 每个试验结果出现的可能性相同。
蒲丰 4040 2048 0.5069
皮尔逊 12000 6019 0.5016
皮尔逊 24000 12012 0.5005
医药数理统计课件

基本事件:不能分解成其它事件的最简单的随机事件. 必然事件:每次试验必然发生() 不可能事件:每次试验都不会发生()
医药数理统计课件
事件与概率
二、事件间的关系与运算
事件的包含:如果事件A发生必然导致B发生 则称事件B包 含事件A 或称事件A包含于事件B 或称A是B的子事件 记作 BA或AB
量取这些可能值的概率是确定的,则称这种变量是随机变量。
注意:随机变量常用X,Y,Z表示,而表示随机变量所取的值通常用x,y,z表示。
例如,从某一学校随机选一学生,测量他的身高。我们可把可能的身高看作随机 变量X,然后提出关于X的各种问题。如P(X>1.7)=?P(X≤1.5)=? P(1.5<X<1.7)=?一旦我们实际选定了一个学生并量了他的身高之后,我们就 得到X的一个具体的值,记作x。这时,要么x≥1.7米,要么x <1.7米,再去求 P(x≥1.7米)就没有什么意义。
则:A B C D F是两两不相容事件 P与F是互为对立的事件 即有PF A B C
D均为P的子事件 且有PA∪B∪C∪D
医药数理统计课件
事件与概率
三、随机事件的运算律
1 关于求和运算 (1) A∪BB∪A (交换律) (2) (A∪B )∪CA∪(B∪C )A∪B∪C (结合律)
2 关于求交运算 (1) A∩BB ∩A (交换律) (2) (A∩B )∩CA∩(B ∩C )A∩B ∩C (结合律)
在二项分布中,X取不同值k(k=0, 1, 2…, n)的概率是不同的, 是P(X=k)取最大值的k(记为k0)称为二项分布的最可能值。当k在(n+1)p附
说明:AB属于A的每一个样本点一定也属于B 对任意事件A 易知A
《医学统计学》教学大纲(医学检验)

《医学统计学》课程教学大纲(Medical Statistics)一、课程基本信息课程编号:14232080课程类别:专业必修课适用专业:医学检验技术学分:理论教学学分:2学分,实验学分:0.5学分总学时:40学时(其中讲授学时:24学时;实验(上机)学时:16学时)先修课程:医学基础课程后续课程:医学检验、预防医学选用教材:李康主编:医学统计学(第6版)[M].北京:人民卫生出版社,2013必读书目:[1]方积乾主编.医学统计学(第7版)[M].北京:人民卫生出版社,2013[2]袁兆康.医学统计学[M].北京:人民军医出版社.2013[3]张文彤主编.SPSS统计分析基础教程(第2版)[M].北京:高等教育出版社,2011选读书目:[1] 颜虹, 医学统计学[M]. 北京:人民卫生出版社,2005[2] 康晓平,实用卫生统计学 [M].北京:北京大学医学出版社,2002[3] Belinda Barton,Medical Statistics: A Guide to SPSS, Data Analysis and Critical Appraisal [M].美国:WILEY Blackwell,2014二、课程教学目标通过本门课程的学习,要使学生学会人群健康研究的统计学方法,学会数值变量和分类变量资料的分析,配对资料的分析,直线相关和直线回归,非参数统计方法,病例随访资料分析。
其目的使大家具备新的推理思维,结合专业问题合理设计试验,科学获取资料,提高科研素质。
本课程教学的主要方法有理论讲授、课堂讨论、实验实习、课堂演算、统计软件SPSS上机等。
通过实验实习,使学生加深对理论的理解。
三、课程教学内容与教学要求1.绪论教学要求:掌握:同质与变异,总体、个体和样本,变量的分类,统计量与参数,抽样误差,频率与概率等基本概念。
理解:统计工作的基本步骤,医学统计学的主要内容。
了解:学习统计学的目的和要求。
医药数理统计教案(人力资源管理)

广东药学院课堂教案学年/学期2008/2009学年第一学期课程名称概率论与数理统计/63学时专业/方向公共事业管理07 公共事业(药事管理)07(1)(2) 人力资源管理(医药人力资源管理方向)07(1)(2)院系部基础学院教研室数学授课教师董健卫或者你才在上一个洞吞了柏忌,下一个洞你就为抓了老鹰而兴奋不已。
广东药学院教务处只有凭借毅力,坚持到底,才有可能成为最后的赢家。
这些磨练与考验使成长中的青少年受益匪浅。
在种种历练之后,他们可以学会如何独立处理问题;如何调节情绪与心境,直面挫折,抵御压力;如何保持积极进取的心态去应对每一次挑战。
往往有着超越年龄的成熟与自或者你才在上一个洞吞了柏忌,下一个洞你就为抓了老鹰而兴奋不已。
广东药学院课堂教案日期学时 2授课内容(章/节)随机事件及其运算(§1.1)教学目的和要求1.了解随机事件、频率的概念、概率的统计定义;2.理解样本空间和样本点的概念;3.掌握随机事件的运算规则。
教学内容[标明重点、难点]1.随机试验,样本空间,随机事件;2.事件的关系和运算* ;只有凭借毅力,坚持到底,才有可能成为最后的赢家。
这些磨练与考验使成长中的青少年受益匪浅。
在种种历练之后,他们可以学会如何独立处理问题;如何调节情绪与心境,直面挫折,抵御压力;如何保持积极进取的心态去应对每一次挑战。
往往有着超越年龄的成熟与自或者你才在上一个洞吞了柏忌,下一个洞你就为抓了老鹰而兴奋不已。
(标记*内容为重点内容)教学方法及教学手段多媒体课件+板书作业习题一1,2只有凭借毅力,坚持到底,才有可能成为最后的赢家。
这些磨练与考验使成长中的青少年受益匪浅。
在种种历练之后,他们可以学会如何独立处理问题;如何调节情绪与心境,直面挫折,抵御压力;如何保持积极进取的心态去应对每一次挑战。
往往有着超越年龄的成熟与自或者你才在上一个洞吞了柏忌,下一个洞你就为抓了老鹰而兴奋不已。
广东药学院课堂教案日期学时 2授课内容(章/节)随机事件的概率,概率的加法公式(§1.2-§1.3)教学目的和要求1. 了解概率的统计定义;2.掌握概率的古典定义,并能计算基本的古典概型问题;3.理解并掌握概率的基本性质,并能使用概率的加法公式.教学内容[标明重点、难点]只有凭借毅力,坚持到底,才有可能成为最后的赢家。
医药数理统计

–参数(总体量):用来描述和表达总体的数量 特征指标。 –统计量:用来描述和表达样本数量特征的 指标。
总体
数量平均水平 和集中趋势
均数
变异大小和 离散程度
标准差
医药数理统计方法
样本
平均数 x
标准差S
医药数理统计方法
• 误差(error)
– 统计学的误差:观察值与真实值之差;样本统计量的 值与总体参数值之差。
– 资料:在确定总体后,研究者则应对每个观察 单位的某项特征进行测量和观察,这种特征称 为变量。对变量的测量值称为变量值(value of variable)或观察值(observed value),也称资料。
医药数理统计方法
•变异(variation)
–在同一个总体内,各个个体所表现出来的 参差不齐性。
( 2)
n
n
其中:f1,... fk及x1,...xk表示1至k组的频数及组中值
组中值=(本段组上限+本段组上限)/2
(三)均数的性质:
医药数理统计方法
1)均数的计算与样本内的每一个值都 有关
2)若每个xi都乘以相同的数k,则均数也 乘以k 3)若每个xi都加上相同的数A,则均数 也加上A
(四) 均数的应用
– 误差来源
• 系统误差
– 仪器初始状态未调整到零、标准试剂未经校正、医生掌握疗效 标准偏高或偏低、仪器的操作方法、治疗方法等原因,造成观 察测量结果倾向性的偏大偏小。
• 偶然误差
– 随机测量误差:指同一个体(观察单位)多次观测结果之差 – 抽样误差:样本指标与总体指标之差 – 过失性误差:操作人员读数、记录之差错
二、统计工作的步骤
医药数理统计方法
• 设计(design):
医学统计学》教学大纲
卫生统计学教学大纲预防医学专业《卫生统计学》教学大纲(供预防医学、妇幼卫生本科专业用)一、前言卫生统计学是应用概率论和数理统计学的基本原理和方法结合医学卫生实际,研究医学卫生资料和信息的搜集、整理与分析的一门学科。
它是医学、卫生工作者必不可少的一门工具,为考试课程。
讲授本课程的目的是使学生掌握医学(卫生)统计学的基本概念、基本方法和基本技能,培养统计思维方法和分析问题解决问题的能力,以及搜集、整理、分析统计资料的能力。
通过本课程的学习,应能为学习其它课程,阅读专业书刊、论著以及毕业后从事预防医学、妇幼卫生学等相关工作和科研奠定必要的统计学基础。
本课程通过课堂讲授与实习,自学与讨论等方式进行教学。
在教学过程中,贯彻启发性教学的原则,突出对学生统计思维能力和分析能力的培养;贯彻循序渐进、理论联系实际的原则。
同时向同学介绍本学科发展的新动向。
理论讲授要尽量从实例入手,讲清医学统计学的基本概念、基本知识、基本原理和基本方法,以及统计方法的应用条件和优缺点,阐明各种方法的内在联系,培养正确的统计思维方法。
对有关统计公式,只要求了解其意义,用途和应用条件,不必深究其数学原理和推导过程。
实习课要联系讲授的理论知识,结合医学实例,针对不同内容,采用计算分析题,选择题,填空题,讨论题,思考题等多种形式,进行统计分析基本技能的训练。
通过教师分析具体医学资料,启发学生思维,让学生独立完成习题,教师进行个别与集体答疑同步进行的方式以利于活跃思想,培养及开发学生智能。
提倡自学与讨论,可安排部分内容让学生自学,教师提供思考题,学生独立回答,力求充分发挥学生的主观能动性,同时鼓励学生提出阅读专业期刊中遇到的统计问题来进行讨论二、学时分配:章次内容讲课时数实习时数及内容1 绪论、统计表与统计图2 3(计算器的使用)2 计量资料的统计描述 4 3(计量资料的统计描述)3 总体均数的估计和假设检验8 12(总体均数的估计和假设检验)4 分类资料的统计描述 2 3(分类资料的统计描述)6(二项分布和泊松分布应用)5 二项分布和泊松分布 43(χ2检验的应用)6 χ2检验 27 秩和检验 2 3(秩和检验的应用)3(直线回归与相关)8 直线回归与相关 29 寿命表 2 3(寿命表的编制)3(调查设计与实验设计)10 调查设计与实验设计 2合计30 42本课程按72学时安排,讲习各半或实习课比例稍大。
《医学统计学》教学大纲
《医学统计学》教学大纲一、课程介绍1、课程的目的与任务《卫生统计学》是数理统计与预防医学相结合的一门应用学科,是预防医学专业学生的专业基础必修课。
通过学习,使学生掌握统计设计、资料收集、整理和分析的基本理论和基本方法,培养学生的统计思维能力和应用技能,为其学习其它课程和阅读专业书刊、从事预防医学实践、进行科学研究打下必要的统计学基础。
《卫生统计学》教学大纲将卫生统计学理论分为要求牢固掌握、一般掌握和一般了解三个层次,以指导师生教与学。
2、教学手段与方法《卫生统计学》教学分为理论课和实验课。
理论课由教师系统讲解各章节的理论知识,实验课由同学们在教师的指导下,相互讨论,自主完成相应实践的操作。
3、建议使用的教材、参考书目、教学网站(要求注明书名、作者、出版社、版本、出版日期等)①选用教材:《卫生统计学》,方积乾主编,人民卫生出版社,第7版,2012。
②参考书目:(1)《卫生统计学实习指导》,方积乾主编,人民卫生出版社(与前述第7版教材配套),2012。
(2)《医学统计学实习指导教程》,郝元涛主编,中山大学出版社,2008。
③教学网站:医学统计学国家精品课程申报网站/mstat/医学统计学网络精品课程/yxtjx/index.htm医学统计学远程教育精品课程教育网网址:/ 账号:yxtjx 密码:yxtjx公众网网址:/ 账号:yxtjx 密码:yxtjx医学统计学双语教学示范课程/yxtjsy/jsdw/jsdw.asp?id=14、考核方式和成绩构成考核方式包括平时表现(出勤、作业、听课)得分,实验课开卷考试得分和理论课闭卷考试得分。
以上三部分分别占最终成绩的20%,20%和60%。
二、学时分配(学时分配要落实到“篇”或“章”)三、教学要求第一章1、教学内容2、教学基本要求(明确基本要求的三个档次,即掌握、熟悉和了解)3、重点与难点(对各章节的重点、难点内容加以必要的说明)……..修订人: 张晋昕,黄波审核人: 张晋昕第一章绪论1、教学内容医学中统计思维的进化;统计学与公共卫生互相推动;统计学的若干概念;学习统计学的目标与方法。
医学统计学(医学统计方法)教学大纲
医学统计学(医学统计方法)教学大纲(供五年制临床医学、护理、口腔专业)前 言本大纲供五年制医学系临床医学专业、护理专业、口腔专业《医学统计学》(《医学统计方法》教学用,是对医学统计学教学提出的基本要求。
其内容可通过讲课,实习或其它方式进行教学,讲授时不一定按此顺序,可根据情况作些调整。
内容分作二级要求:第一级是学生必须掌握的内容,教师一般应于理论课讲授,亦为实习课与考试的重点。
第二级是要求熟悉的内容,教师应选择性讲授,未讲授部分由学生自学。
本大纲规定教学时数为36学时,其中讲授27学时,实习9学时。
《医学统计学》是应用概率论和数理统计的基本原理和方法,研究医学领域中数据的收集、整理和分析的重要工具。
生物医学的研究对对象是随机现象,其表现不仅受该事物本质规律的制约,同时还受偶然因素的影响,只有用医学统计学方法才能揭示被偶然因素掩盖的本质规律。
学习医学统计学方法对医学科学研究和疾病防治工作有重要意义,是医学生需掌握的基本知识。
第一章 医学统计学的基本内容一、目的和要求㈠ 掌握几个基本概念。
㈡ 熟悉统计资料的基本内容。
㈢ 熟悉统计工作的基本步骤。
㈣ 熟悉统计图和统计表基本内容二、教学内容㈠ 统计中的几个基本概念:总体、样本、变异、概率。
㈡ 统计资料的类型1、计量资料与数值变量2、计数资料与分类变量3、变量的转化㈢ 统计工作的步骤统计工作可分为设计、搜集资料、整理资料和分析资料四个步骤:1、设计2、搜集资料3、整理资料4、分析资料以上四个步骤是紧密联系,不可分割的整体,任何一步的缺陷,都会影响统计分析的结果。
㈣ 统计图和统计表1、统计表的基本结构、种类和编制统计表的注意事项。
2、统计图的概念、绘制统计图的基本要求及常用统计图的绘制方法与注意事项。
第二章 数值变量资料的统计分析第一节 数值变量的统计描述一、目的和要求㈠ 掌握平均水平指标和离散程度的计算方法和各个指标的适用条件。
㈡ 了解频数表的编制方法及用途。
医学统计学教学大纲
医学统计学教学大纲(来自网络教学平台)(供七年制用)预防医学系流行病与卫生统计学教研室2007年2月前言医学统计学是应用概率论与数理统计的原理和方法研究医学中数据的收集、整理与分析的一门应用科学,通过对大量偶然现象的研究,认识其客观规律性,是从事医学研究必须具备的重要工具和研究手段。
通过本课程教学,培养学生科学思维与推断能力,使其掌握:医学统计方法的基本理论、基本方法与技能,具备基本的医学科研设计、统计分析与评价能力,为阅读专业文献、进行科研工作打下良好的统计学基础。
本课程共126学时,其中理论72学时,实验54学时(课堂讨论9学时,统计软件应用45学时)。
理论课程内容主要包括三个部分:第一个部份是医学统计学基本概念和方法(36学时),其中包括总体和样本等基本概念、计量资料和计数资料的统计描述方法、单个样本数据的参数估计、两个或多个样本数据比较的假设检验。
第二个部份是医学科研设计(14学时),其中包括医学科研设计的意义、原则、要素、样本含量估计、抽样方法及常见的几种设计类型。
第三个部份是医用多元统计分析(22学时),其中包括多元统计分析概论、多元线性回归、多元逐步回归、判别分析、聚类分析、Logistic回归、Cox回归。
本大纲适用于七年制学生。
第一章绪论一、教学目的要求:了解医学统计学的意义、统计工作的基本步骤;熟悉资料的统计分类及几个重要分布——正态分布、二项分布、泊松分布;掌握以下基本概念:同质与变异、总体与样本、总体研究与抽样研究、误差、概率与小概率事件。
二、教学重点、难点:重点:基本概念:同质与变异、总体与样本、总体研究与抽样研究、误差、概率与小概率事件。
难点:几个重要分布——正态分布、二项分布、泊松分布。
三、教学方法:课堂讲授。
第二章计量资料的统计描述一、教学目的要求:1、了解频数分布表的编制, 并据此描述资料的频数分布特征;2、掌握各种平均数指标的计算及其适用条件,尤其是均数;3、掌握各种离散趋势指标的计算及其适用条件,尤其是标准差,熟悉标准差的意义及应用;4、掌握正态分布理论的重要应用:医学参考值范围的估计。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
医药数理统计方法教学大纲(供成人专科班使用)(2018年4月修订)I前言《医药数理统计方法》是研究和揭示随机现象中统计规律的数学学科。
数理统计方法的应用广泛,几乎遍及所有科学技术领域,是各学科中分析与解决咨询题的差不多工具。
《医药数理统计方法》课程,是医科各专业的一门重要的基础课,要紧程讲述概率论与数理统计的概念和方法,学习的目的旨在培养学生逻辑推理和运算能力、分析咨询题和解决咨询题的能力,以学习和把握统计方法为重点,学会如何样有效地收集、整理和分析带有随机性的数据,以对实际咨询题做出推断或推测、并为采取一定的决策和行动提供依据和建议。
使学生初步把握处理随机现象的差不多思想与方法,具备分析和处理带有随机性数据的能力,为学习后续相关基础课程与专业课程提供基础理论和相关知识。
本大纲供成人专科班使用。
本大纲使用讲明如下:1.大纲按要求分为“了解”、“熟悉”和“把握”三个层次,“了解”是指对概念和理论方面的要求;“熟悉”和“把握”是对方法、运算和应用的低层次和较高层次的要求。
2.为使用方便,大纲正文中将重点内容加了下划虚线(如数学期望),将核心内容加了下划线和着重号(如数学期望),使用者要对这部分内容引起足够重视。
3.本课程教学参考时数:36学时。
Ⅱ正文一、教学目的学习概率论的目的是为了研究看似无规律的随机现象的数量规律,通过中学所学的频率和排列组合的知识,来明白得概率的定义与运算。
古典概型是运算概率最重要的方法之一,要明白得并把握。
事件之间的关系和运算与中学所学的集合论知识极其类似,只是讲法和记法有所不同。
古典概型、加法定理、乘法定理、全概率公式与逆概率公式是本单元的核心内容,通过学习要把握其方法和应用。
二、教学要求1.把握概率的性质;把握利用古典概型(率)求事件的概率;把握概率的加法定理(公式)及其运算;把握概率的乘法定理(公式)及其运算;把握全概率公式、逆概率公式及其应用。
2.熟悉事件间的差不多关系和运算规律;熟悉两事件独立的充分必要条件。
3.了解随机事件、事件的频率与概率的概念;了解古典概型(率)的概念,三、教学内容1.随机事件的概率:随机事件的概念,事件的频率与概率的概念。
概率的性质。
2.古典概型(率),概率的性质。
3.事件间的相互关系。
事件间的包含与相等,和与积,互不相容事件,对立事件,事件间的运算规律。
4.概率的运算。
概率的加法定理(公式),条件概率与概率的乘法定理(公式),事件独立的充分必要条件。
5.全概率公式与逆概率公式。
第二章随机变量及其分布一、教学目的随机变量有不于高等数学中变量的概念,借助它能够利用高等数学的知识和方法方便的研究随机现象。
通过本单元的学习,明白得随机变量的含义以及常见的两类随机变量,搞清晰概率函数、概率密度与分布函数的定义、性质、运算与应用,学会运算简单的离散型和连续型随机变量的概率函数和分布函数。
对常见的几种分布(二项分布、泊松分布与正态分布是三个最为重要的分布)要熟练把握。
二、教学要求1.把握二项分布与泊松分布的概率函数;把握正态分布(含标准正态分布)的概率密度、分布函数及其性质。
2.熟悉利用二项分布和泊松分布运算概率。
3.了解随机变量的概念;了解离散型随机变量的概率函数的概念;了解分布函数的概念及其性质;了解连续型随机变量的概率密度及其性质。
三、教学内容1.随机变量与离散型随机变量的分布。
随机变量的概念,离散型随机变量的概念,离散型随机变量的概率函数,二项分布与泊松分布及其概率运算。
2.分布函数与连续型随机变量的分布分布函数的概念及其性质,连续型随机变量的概念,随机变量的概率密度及其性质,正态分布(含标准正态分布)的概率密度及分布函数,正态分布的性质。
第三章随机变量的数字特点一、教学目的随机变量的数字特点要紧包括数学期望(也称集中趋势或总体均数)、方差(稳固性指标)等。
百分位数、四分位数、中位数、众数等也是用于刻画位置参数的。
离散型和连续型的数学期望的定义有所不同,数学期望和方差的性质也不相同。
学习本单元,要学会运算随机变量的数学期望、方差,了解正态随机变量的形成机制。
变量的标准化运算及其思维贯穿整个课程,一定要引起重视。
二、教学要求1.把握数学期望的性质和常见随机变量(二项分布、泊松分布、正态分布等)的数学期望;把握正态变量的标准化运算以及标准化随机变量。
2.熟悉方差的性质和常见随机变量(二项分布、泊松分布、正态分布等)的方差;熟悉百分位数、中位数、与众数的概念及运算。
3.了解离散型随机变量和连续型随机变量数学期望(均数)的概念;了解方差、标准差、矩的概念;了解二项分布的正态近似和泊松分布的正态近似。
三、教学内容1.数学期望离散型随机变量的数学期望,连续型随机变量的数学期望,数学期望的性质,二项分布,泊松分布,正态分布的数学期望。
2.方差方差、标准差的概念,方差的性质,泊松分布、正态分布的方差。
3.正态变量的标准化运算以及标准化随机变量。
4.常见的三种分布的渐近关系。
二项分布的正态近似,泊松分布的正态近似。
5.矩的概念。
6.百分位数、中位数、与众数的概念及运算一、教学目的本单元学习统计学的差不多概念,在此基础上学习体会分布和常见的几种分布,它们是统计学的基础知识。
通过学习为后面的统计推断打下必要的理论基础。
2χ分布、t分布与F分布的部分推导偏难,可做一样了解,但相关重要的结论要求把握。
参考值范畴是一个专门重要的统计指标,要求把握。
二、教学要求1.把握用运算器运算样本均数、样本方差、样本标准差等。
2.熟悉2χ分布、t分布与F分布的性质;熟悉查2χ分市、t分布与F分布的临界值(单、双侧)表。
3.了解样本(随机样本)、样本均数、样本方差、统计量、标准误等概念;χ分布、t分布与F分布的概念;了解临界值的概念。
了解均数的分布特点。
了解2三、教学内容1.样本与统计量。
样本(随机样本)的概念,样本均数、样本方差的概念,统计量、标准误的概念。
2.和的分布与均数的分布的相关结论。
3.2χ分布、t分布和F分布。
2χ分布的概念和性质,t分布的概念和性质,F分布的概念和性质,4.临界值的概念,单侧临界值与双侧临界值的概念。
第五章抽样估量一、教学目的本单元学习参数估量的有关内容。
参数估量是利用样本的信息来估量总体的未知参数,要紧包括点估量和区间估量。
通过学习,学会利用样本信息来估量总体信息的思想和方法,把握三个常见分布(正态分布、二项分布和泊松分布)参数的估量方法,学会设计参数估量的样本量。
二、教学要求1.把握寻求参数的置信区间的方法与步骤;把握正态总体参数(均数和方差)的区间估量方法。
2.熟悉样本均数和样本方差分不是总体均数和总体方差的无偏估量量;熟悉矩估量的概念;熟悉二项分布和泊松分布参数的区间估量方法。
3.了解点估量和点估量量(统计量)的概念;了解无偏估量量;了解有效估量量和一致估量量的概念;了解区间估量的概念;了解正态总体均数估量的样本量,总体率估量的样本量。
三、教学内容1.点估量与区间估量点估量的概念,点估量量(统计量)的概念,无偏估量量的概念,有效估量量的概念,一致估量量的概念,区间估量的概念。
2.正态总体参数的区间估量。
均数的区间估量,方差的区间估量。
3.二项分布和泊松分布参数的区间估量。
二项分布参数的区间估量,泊松分布参数的区间估量。
4.参数估量的样本量正态总体均数估量的样本量,总体率估量的样本量。
一、教学目的假设检验是考察由样本信息所得到的总体参数是否具有显著性差异(统计学意义),其差不多原理是利用小概率事件的原理动身构造概率反证法。
它与学生在中学所学的一般逻辑意义下的反证法不同。
要专门好的明白得概率反证法的差不多原理,把握一样假设检验的方法的步骤,重点学会P值法。
把握大样本总体率的检验方法,熟悉泊松分布参数的检验。
把握参数检验的试验设计中样本量的估量方法。
二、教学要求1.把握P值方法,临界值方法、置信区间法的原理、方法与步骤;把握单个正态总体的假设检验方法(包括2σ已知时单个正态总体均数的u检验、2σ未知时单个正态总体均数的t检验,单个正态总体方差的2χ检验);把握单个二项分布总体参数的u检验;把握单个泊松分布总体参数的u检验;把握参数检验的样本量估量方法。
2.熟悉同意域、拒绝域、单侧检验、双侧检验等概念;熟悉各种检验的条件、统计量;熟悉单侧检验与双侧检验、拒绝域与同意域;熟悉具有方差齐性的两个正态总体均数的t检验;熟悉比较两个独立大样本二项分布总体参数的检验;熟悉比较两个独立大样本泊松分布总体参数的检验。
3.了解零假设(原假设)、对立假设(备择假设)等概念;了解假设检验的思想方法;了解单个正态总体均数的配对t检验;了解均数未知时两个正态总体方差齐性的F检验。
三、教学内容1.假设检验的概念。
小概率事件的原理,概率反证法的原理。
零假设(原假设)、对立假设(备择假设),检验水平(显著性水平),两类错误,单侧检验、双侧检验,拒绝域、同意域等概念。
2.单个正态总体的假设检验。
2σ已知时单个正态总体均数的u检验;P值方法、置信区间法、临界值法;2σ未知时单个正态总体均数的t检验;单个正态总体均数的配对t检验;单个σ检验。
正态总体方差的23.两个正态总体的假设检验具有方差齐性的两个正态总体均数的t检验;均数未知时两个正态总体方差齐性的F检验。
4.单个总体的检验单个二项分布总体参数的检验;单个泊松分布总体参数的检验。
5.两个总体的检验比较两个独立大样本二项分布总体参数的检验;两个独立大样本泊松分布总体参数的检验。
6.参数检验的样本量估量方法。
Ⅲ教学组织与方法1.实施机构:医学工程技术学院数学教研室。
2.组织内容:教案讲义审核、集体教学备课、教学方法研究、教学手段应用等。
3.教学方法:要紧采取理论教学,采纳启发式、讨论式、讲授与练习相结合等课堂教学方式,结合多媒体教学手段进行教学。
“重点(把握)”咨询题要保证讲透,“熟悉”咨询题要讲够,“了解”咨询题要作简单介绍。
4.课外作业与练习:每堂课布置适量的作业,要求学生独立完成,并要求做一定量的练习和摸索题,以熟悉和巩固所学内容。
5.辅导形式:辅导要紧采取教师集中辅导和答疑,个不学生的咨询题可到教师办公室咨询。
6.考核类型:本课程为必修随堂考试(考察)课程。
7.考试形式:考试采纳闭卷笔试方式,考试不及格者必须参加课程补考。
总成绩以百分运算,并参考单元测验和平常作业等成绩。
采纳教考分离、流水评卷,作到客观、公平。
8.考试时刻:考试在课程终止后由学院安排,教研室组织考试。
Ⅳ学时数分配表。
