圆度的定义、测量和计算
圆度和同心度的关系
圆度和同心度的关系引言圆度和同心度是几何学中常用的两个概念，它们描述了图形的形状和结构。
在本文中，我们将探讨圆度和同心度之间的关系，以及它们在不同领域中的应用。
首先，我们将介绍圆度和同心度的定义和计算方法，然后探讨它们之间的联系。
圆度的定义与计算方法圆度是描述一个图形接近于圆形程度的量化指标。
一个完美的圆具有最大的圆度值为1，而越偏离圆形则圆度值越小。
在工程学中，圆度常用于评估零件加工精度或测量设备精确性。
计算一个图形的圆度可以通过计算其最大半径与最小半径之间的比值来得到。
具体而言，对于一个闭合曲线或凸多边形，可以通过找到其内切最大圆（内接最小正方形）和外切最小圆（外接最大正方形）来计算。
对于一个闭合曲线或凸多边形，我们可以通过以下步骤计算其圆度： 1. 找到最小正方形，其边界刚好与曲线或多边形的边界相切。
2. 计算最小正方形的半径。
3. 找到最大正方形，其内部刚好包含曲线或多边形。
4. 计算最大正方形的半径。
5. 圆度 = 最小正方形的半径 / 最大正方形的半径。
同心度的定义与计算方法同心度是描述一组图形共享相同中心点程度的量化指标。
在几何学中，同心度常用于评估几何结构的对称性和精确性。
计算一组图形的同心度可以通过计算它们各自中心点之间的偏差来得到。
具体而言，假设我们有n个图形，每个图形都有一个中心点坐标(x, y)，我们可以通过以下步骤计算它们的同心度： 1. 计算每个图形中心点与参考中心点之间的距离。
2. 将所有距离求和并除以n-1（其中n为图形数量）得到平均距离。
3. 同心度 = 平均距离 / 参考中心点到任意一个图形中心点之间的距离。
圆度和同心度的关系圆度和同心度都是描述几何结构形状和结构的量化指标，它们之间存在一定的关系。
首先，一个完美的圆具有最大的圆度值1，它也是一个具有最大同心度的图形。
这是因为一个完美的圆在任何角度上都对称，并且所有点到中心点的距离都相等。
其次，当图形的圆度接近于1时，它的同心度也会增加。
圆度和圆柱度的测量步骤
圆度和圆柱度的测量步骤
圆度和圆柱度是常用的测量参数，用于描述物体表面的圆形度和直线度。
以下是测量圆度和圆柱度的一般步骤：
1. 准备测量设备：需要使用一个合适的测量工具，如千分尺、测微计或投影仪等，以及支撑物。
2. 放置被测物体：将被测物体放置在水平的支撑物上，确保物体稳定且没有移动。
3. 定位测量点：确定需要测量的地方，并标记好测量点。
4. 测量圆度：使用测量工具在标记的测量点上进行测量，记录下测量结果。
对多个测量点进行重复测量，并取得平均值。
5. 计算圆度：将测量结果与理论圆形进行比较，计算圆度误差。
可以使用公式或者专门的软件进行计算。
6. 测量圆柱度：将测量工具放置在被测物体上，并旋转物体，观察测量工具的指示值。
可以根据需要在不同位置旋转并进行多次测量，以得到更准确的结果。
7. 计算圆柱度：将测量结果与理论直线进行比较，计算圆柱度误差。
同样可以使用公式或者软件进行计算。
8. 分析结果：根据测量结果和误差值进行分析，判断被测物体的圆形度和直线度是否满足要求。
请注意，以上是一般的测量步骤，具体的操作可能因测量设备和被测物体的不同而有所差异。
圆度,圆柱度及球度的测量及评价方法讲解
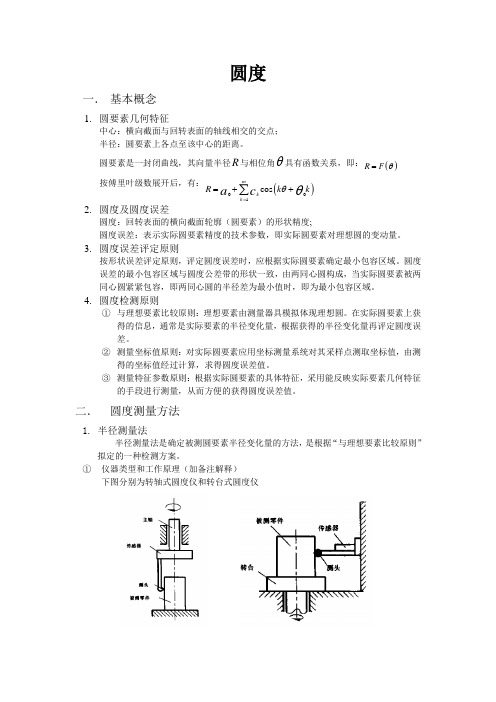
圆度一． 基本概念1. 圆要素几何特征中心：横向截面与回转表面的轴线相交的交点； 半径：圆要素上各点至该中心的距离。
圆要素是一封闭曲线，其向量半径R 与相位角θ具有函数关系，即：()R F θ=按傅里叶级数展开后，有：()001cos mk k R k k a c θθ==++∑2. 圆度及圆度误差圆度：回转表面的横向截面轮廓（圆要素）的形状精度;圆度误差：表示实际圆要素精度的技术参数，即实际圆要素对理想圆的变动量。
3. 圆度误差评定原则按形状误差评定原则，评定圆度误差时，应根据实际圆要素确定最小包容区域。
圆度误差的最小包容区域与圆度公差带的形状一致，由两同心圆构成，当实际圆要素被两同心圆紧紧包容，即两同心圆的半径差为最小值时，即为最小包容区域。
4. 圆度检测原则① 与理想要素比较原则：理想要素由测量器具模拟体现理想圆。
在实际圆要素上获得的信息，通常是实际要素的半径变化量，根据获得的半径变化量再评定圆度误差。
② 测量坐标值原则：对实际圆要素应用坐标测量系统对其采样点测取坐标值，由测得的坐标值经过计算，求得圆度误差值。
③ 测量特征参数原则：根据实际圆要素的具体特征，采用能反映实际要素几何特征的手段进行测量，从而方便的获得圆度误差值。
二． 圆度测量方法1. 半径测量法半径测量法是确定被测圆要素半径变化量的方法，是根据“与理想要素比较原则”拟定的一种检测方案。
① 仪器类型和工作原理（加备注解释）下图分别为转轴式圆度仪和转台式圆度仪圆度仪可运用测得信号的输出特性，将被测轮廓的半径变化量放大后同步自动记录下来，获得轮廓误差的放大图形，可按放大图形评定圆度误差。
② 用圆度仪测量注意事项（加备注择项解释）选择适当的侧头类型；静态测量力选择；测量平面和测量方向确定；频率响应选择；选择适当的放大倍率；正确安装被测件，径向偏心和轴向倾斜；主轴误差的影响2. 坐标测量法坐标测量法是根据测量坐标值原则提出的一种检测方案。
圆度的范围
圆度的范围圆度是指一个圆形物体表面的平滑程度和几何形状的规整程度。
在工业制造和机械加工中，圆度是一个非常重要的指标，因为它直接影响到零件的质量和性能。
圆度的范围是指在实际生产中，圆度的允许误差范围。
下面将详细介绍圆度的范围及其影响因素。
一、圆度的定义和测量方法圆度是指一个圆形物体表面的平滑程度和几何形状的规整程度。
在工业制造和机械加工中，圆度是一个非常重要的指标，因为它直接影响到零件的质量和性能。
圆度的测量方法有很多种，其中比较常用的是三点法和两点法。
三点法是指用三个测量点来确定圆形物体的圆心和半径，从而计算出圆度误差。
两点法是指用两个测量点来确定圆形物体的直径，从而计算出圆度误差。
二、圆度的范围圆度的范围是指在实际生产中，圆度的允许误差范围。
不同的零件和工艺要求对圆度的要求不同，因此圆度的范围也有所不同。
下面将介绍一些常见的圆度范围。
1. 一般圆度范围一般情况下，圆度的允许误差范围为0.01mm~0.05mm。
这个范围适用于一些一般的机械零件，如轴承、齿轮、轴等。
在这个范围内，圆度误差对零件的性能影响较小，可以满足一般的使用要求。
2. 高精度圆度范围对于一些高精度的零件，如精密机床、光学仪器等，圆度的允许误差范围要求更高，一般为0.001mm~0.005mm。
在这个范围内，圆度误差对零件的性能影响较大，需要采用更加精密的加工工艺和测量方法来保证圆度的精度。
3. 超高精度圆度范围对于一些超高精度的零件，如半导体芯片、光学元件等，圆度的允许误差范围更加严格，一般为0.0001mm~0.001mm。
在这个范围内，圆度误差对零件的性能影响非常大，需要采用最先进的加工工艺和测量方法来保证圆度的精度。
三、影响圆度的因素圆度的精度受到很多因素的影响，下面将介绍一些常见的影响因素。
1. 加工工艺加工工艺是影响圆度精度的最重要因素之一。
加工工艺的不同会导致零件表面的粗糙度、形状和尺寸等方面的差异，从而影响圆度的精度。
简述圆度和圆柱度公差的区别
简述圆度和圆柱度公差的区别圆度和圆柱度公差都是机械加工中非常重要的参数，他们分别用于描述零件圆度和圆柱度的精度。
下面将详细讨论这两个公差的定义，区别，计算以及重要性。
圆度公差定义圆度公差是描述零件外表面上所有圆形的形状与理论圆之间的偏差大小。
即零件的距离理论圆的最大距离和最小距离的差值。
圆度公差可以用一个形状公差带来表示。
形状公差是用一条线描述理论几何元素的随意变化。
这个带子是距离理论外径和内径沿着周向平均值的上限和下限。
1. 描述的几何形状不同。
圆度公差是用来描述零件外表面上的所有的圆形，而圆柱度公差是用来描述零件直径上的面形误差。
2. 公差计算单位不同。
圆度公差的计算单位是长度，而圆柱度公差的计算单位是角度。
3. 表示方法不同。
圆度公差使用形状公差带表示，而圆柱度公差通常使用有限制的形状公差带表示。
圆度公差的计算通常通过在零件外径和内径上测量一些点，然后计算这些点距离理论圆的偏差。
可以通过下面的公式来计算公差大小：T = Tmax - Tmin其中，T代表公差大小，Tmax代表距离理论圆的最大距离，Tmin代表距离理论圆的最小距离。
圆度公差和圆柱度公差对于机械加工的质量和可靠性都非常重要。
准确地控制圆度和圆柱度公差可以确保机件在使用中的运动精度，减少零件之间的摩擦和磨损，延长机器的寿命。
由于圆度公差和圆柱度公差是直接影响机械加工质量和可靠性的参数，因此机械加工和制造行业非常注重这些公差的控制和管理。
在机械加工过程中，如果控制不好这两个公差，可能会导致机械零件不能精确地嵌合和运动，使设备失去运行能力，或者造成严重的机械故障，影响工作效率。
一旦发生，这些问题会给制造工厂和使用者带来巨大的损失。
因此，准确地控制圆度公差和圆柱度公差对于获得优质的机械零件是必不可少的。
为了确保零件质量和性能，机械加工行业必须重视圆度公差和圆柱度公差的控制，不断提高技术水平和生产水平，以满足客户的需求和要求。
为了准确地控制圆度公差和圆柱度公差，机械加工行业需要采用适当的加工方法和工具，并制定合理的加工工艺和操作规程。
圆度测量标准
圆度测量标准
圆度测量是衡量物体表面的圆形度或曲率的一种方法。
它可用来判断物体的圆形度是否达到一定的标准要求。
一般来说，圆度测量标准包括以下几个方面：
1. 公差要求：即物体表面允许的最大偏离理想圆形度的范围。
常见的公差标准包括ISO标准、ASME标准等。
2. 测量仪器要求：测量圆度需要使用专门的测量仪器，如圆度仪、CMM（Coordinate Measuring Machine）等。
测量仪器的精度、稳定性等要求也需要进行规定。
3. 测量方法要求：测量圆度的方法多种多样，包括机械测试、光学测试、电子测试等。
标准中需要明确规定使用哪种方法进行测量，以及测量参数的要求。
4. 评价指标要求：用于评价圆度的指标有很多，如最大偏离、平均偏离、波动率等。
标准中需要明确规定评价指标的选择和计算方法。
5. 报告和记录要求：对于圆度测量结果的报告和记录也需要进行规范。
标准中会明确要求记录哪些信息，如测量日期、测量人员、测量仪器型号等。
需要注意的是，不同的行业和应用领域对圆度的要求不同，因
此圆度测量标准也会有所差异。
用户需要根据具体的需求选择相应的标准进行测量和评价。
moldflow圆度测量方法-概述说明以及解释
moldflow圆度测量方法-概述说明以及解释1.引言1.1 概述本文旨在介绍moldflow圆度测量方法，该方法用于评估注塑成型过程中圆形零件的精度和质量。
圆度测量是指对圆形零件的直径、圆心位置和圆度误差进行测量和分析，以评估零件的几何形状是否符合设计要求。
在注塑成型过程中，圆度是一个重要的质量指标，因为许多零件需要具有高精度的圆形形状，如轴承、密封圈等。
圆度误差可能导致零件的不完全贴合、泄漏或摩擦增加，进而影响零件的正常使用。
因此，准确地测量和控制圆度误差对于保证产品的性能和质量是至关重要的。
本文将重点介绍三种常用的moldflow圆度测量方法。
第一种方法是基于投影仪的圆度测量方法，通过对圆形零件的投影图像进行分析，可以获得直径和圆度误差的信息。
第二种方法是使用三坐标测量机进行圆度测量，该方法可以对零件的三维形状进行全面测量，提供更详细的几何参数。
第三种方法是利用激光扫描仪进行圆度测量，该方法非接触式测量，具有高速度和高精度的特点。
本文将详细介绍上述三种测量方法的原理、优缺点以及适用范围，并根据实际应用场景进行比较分析。
此外，我们还将对现有方法的局限性和改进方向进行讨论，以期为圆度测量方法的进一步研究和应用提供一定的指导。
通过本文的阅读，读者将能够了解不同的moldflow圆度测量方法，并根据实际需求选择适合的方法来评估和改进圆形零件的精度和质量。
1.2 文章结构文章结构部分的内容可以按照以下方式编写：文章结构本文将按照以下结构进行探讨和分析Moldflow圆度测量方法。
首先，在引言部分，我们将对文章进行简要概述，并明确文章的目的。
接下来，正文部分将介绍三种常用的Moldflow圆度测量方法，并详细介绍每种方法的原理、步骤和适用范围。
其中，第一种方法是基于XX原理的圆度测量方法，第二种方法是基于XX原理的圆度测量方法，第三种方法是基于XX原理的圆度测量方法。
在结论部分，我们将对整篇文章进行总结，并分析每种方法的优缺点及实际应用价值。
圆度及圆柱度的参数配图全解
圆度及圆柱度的参数配图全解1.参数和定义参考参考圆是用某种规则匹配测量数据得到的相关圆，据此参考圆计算得到圆度的有关参数。
最小二乘参考圆(LSCI)计算得到的最小二乘参考圆与其内外数据差值的平方和最小。
该圆普遍被用作参考圆。
P=最高峰值 V=最低谷值计算得到的最小区域参考圆是两个完全包容测量数据的同心圆，这两圆之间的径向间距最小。
P=最高峰值 V=最低谷值最小外接参考圆(MCCI)计算得到的最小外接参考圆是完全将测量数据包容在内的最小圆。
V=圆度计算得到的最大内切参考圆是完全被测量数据包容在内的最大圆。
P=圆度倾斜纠正当测量的圆柱轴线建立后，当它与主轴轴线不平行时，它与主轴轴线在空间某个方向的倾斜将使测量数据发生椭圆畸变。
本选项允许在相对于圆柱轴线进行进一步计算之前，从单个圆度测量数据中去除该椭圆度。
偏心度E偏心值是所选基准轴(点)到所分析参考圆中心的距离。
偏心角为主轴零度位置与参考圆中心和基准轴连线之间的夹角。
A=基准点 B=数据中心 E=偏心值θ=偏心角(上图为315˚)偏心角为主轴零度位置与参考圆中心和基准轴连线之间的夹角。
A=最小二乘中心 B=最小二乘参考圆 C=角度θE=偏心 D=回转中心跳动两个同心圆的径向间隔，这两个圆与基准轴(或点)同心，并完全包容测量数据，即指示器读数的总变动量。
(ISO 1101; DIN 7184; BS.308第三部分)。
A=跳动 B=距基准点最近的数据点 C=基准点D=距基准点最远的数据点R此值取决于径向横臂的标定(为标尺的目视读数)，仅供参考。
谐波分析数据用傅立叶级数表示。
删除点为从任何间断数据的两边删除的点的个数。
它们是从所选数据总数中删除的。
平面度平面度可用最小二乘或最小区域方法来定义。
最小二乘基准拟合一平面，测量数据至该平面差值的平方和最小。
最小区域基准拟合两个平行平面，使其完全包容测量数据，且间隔最小。
A=轴线 F=平面度LS=最小二乘基准“参考平面垂直度”值是两个平行平面最小轴向间隔，这两个平面垂直于参考轴线，并且完全包容由被测数据拟合的最小二乘平面。
形位公差定义及检测方法
形位公差定义及检测方法一、直线度的定义及检测方法定义：直线度是指零件被测的线要素直不直的程度。
检测方法概述：㈠.将平尺（小零件可用刀口尺）与被测面直接接触并靠紧。
此时平尺与被测面之间的最大间隙即为该检测面的直线度误差。
一般公用检测器具-塞尺。
（图片）按此方法检测若干条素线，取其中最大误差值作为该件的直线度误差。
㈡.将被测件放在平台上，并靠紧方箱或直角尺（或者将被测件放置在等高V型铁上）。
用杠杆表在被测素线的全长范围内测量，同时记录检测数值，最大数值与最小数值之差即为该条素线直线度误差。
（简图）：按上述方法测量若干条素线，并计算，取其中最大的误差值，作为被测零部件的直线度误差。
㈢将被测零部件用千斤顶支起，利用杠杆表将被测素线的两端点调整到与平台平行，在被测素线的全长范围内测量，同时记录，读数，最大值与最小值之差即为该素线的直线度误差，按同样方法测量若干条素线，取其中最大的误差值作为该被测件的直线度误差。
㈣综合量规：综合量规的直径等于被测零件的实效尺寸，综合量规必须通过被测零件。
二、平面度定义及检验方法平面度是指零件被测表面的要素平不平得程度。
㈠将被测件用千斤顶支撑在平台上，调整被测表面最远的三点A,B,C，（利用杠杆表或高度尺）使其与平台平行，然后用测头在整个实际表面上进行测量，同时记录读数，其最大与最小读数之差，即为被测件平面度误差。
㈡用刀口尺（小型件）或平尺（较大型件）在整个被测平面上采用“米”字型或栅格型方法进行检测，用塞尺进行检验，取其塞尺最大值为该被测零件得平面度误差。
㈢环类垫圈类零件将被测件的被测面放在平台上，压紧，然后用塞尺检测多处，其塞入的最大值即为该件的平面度误差。
（或者将被测件的被测面用三块等高垫铁在平台上均分支撑，然后用杠杆表在被测面的多处进行检测，取其最大与最小读数的差作为该件的平面度误差。
三、圆度定义及测量方法定义：圆度是指具有圆柱面（包括圆锥面）的零件在同一横剖面内的实际轮廓不圆的程度。
钢球加工圆度计算公式
钢球加工圆度计算公式在工程加工中，圆度是一个非常重要的参数，它直接影响着产品的质量和性能。
而钢球加工圆度计算公式则是评定钢球加工质量的重要指标之一。
本文将介绍钢球加工圆度计算公式的相关知识，以及其在工程加工中的应用。
钢球加工圆度计算公式是用来评定钢球加工质量的重要指标之一。
圆度是指一个圆形物体的表面与其理论轴线之间的偏差程度。
在钢球加工中，圆度的计算是非常重要的，因为它直接影响着钢球的质量和性能。
一个圆度较高的钢球，其表面与理论轴线之间的偏差较小，质量较高，性能也较好。
因此，钢球加工圆度计算公式对于评定钢球加工质量具有非常重要的意义。
钢球加工圆度计算公式通常采用以下公式进行计算：圆度=（最大直径-最小直径）/平均直径。
其中，最大直径是指钢球表面上的最大直径，最小直径是指钢球表面上的最小直径，平均直径是指最大直径和最小直径的平均值。
通过这个公式，可以很直观地计算出钢球的圆度，从而评定钢球的加工质量。
在工程加工中，钢球加工圆度计算公式通常会结合实际测量数据进行计算。
通过使用测量仪器对钢球的直径进行测量，然后根据上述公式进行计算，得出钢球的圆度。
通过这种方法，可以很直观地评定钢球的加工质量，从而及时发现和解决加工中的问题，提高产品的质量和性能。
钢球加工圆度计算公式在工程加工中具有非常重要的应用价值。
通过对钢球的圆度进行计算，可以及时评定钢球的加工质量，从而及时发现和解决加工中的问题，提高产品的质量和性能。
同时，钢球加工圆度计算公式也为工程加工提供了一种科学、准确的评定方法，为产品的质量控制和质量管理提供了重要依据。
除了在工程加工中的应用，钢球加工圆度计算公式也在其他领域具有重要的应用价值。
例如，在机械制造、汽车制造、航空航天等领域，都需要使用钢球，而钢球的圆度对于产品的质量和性能具有重要影响。
因此，钢球加工圆度计算公式在这些领域也具有重要的应用价值。
综上所述，钢球加工圆度计算公式是评定钢球加工质量的重要指标之一，具有重要的应用价值。
直线度 平面度 圆度 圆柱度公差带定义及标注实例
直线度平面度圆度圆柱度公差带定义及标注实例1.直线度是指工件上直线轴线与参考直线轴线之间的距离偏差。
Straightness refers to the deviation distance between the straight axis of the workpiece and the reference straight axis.2.平面度是指工件上平面与参考平面之间的距离偏差。
Flatness refers to the deviation distance between the plane of the workpiece and the reference plane.3.圆度是指工件上圆形轮廓与参考圆形轮廓之间的距离偏差。
Roundness refers to the deviation distance between the circular profile of the workpiece and the reference circular profile.4.圆柱度是指工件上圆柱体轴线与参考圆柱体轴线之间的距离偏差。
Cylindricity refers to the deviation distance between the axis of the cylindrical body on the workpiece and the reference cylindrical body.5.公差带是指允许的尺寸偏差范围，在这个范围内的尺寸都是合格的。
Tolerance zone refers to the allowable range of dimensional deviation, and dimensions within this range are considered acceptable.6.在工程图纸上，直线度通常以符号“⊥”标注。
On engineering drawings, straightness is usually indicated by the symbol "⊥".7.平面度通常在工程图上以字母“F”标注。
圆形度计算公式(一)
圆形度计算公式(一)圆形度计算公式在工程领域中，圆形度是用来衡量一个对象与完美圆形的接近程度的指标。
圆形度计算公式可以帮助我们评估一个物体的圆形度，从而判断其质量和精度。
下面是一些常见的圆形度计算公式及其例子。
1. 圆度误差计算公式圆度误差是指一个物体在各个测量方向上与完美圆形的偏差。
以下是计算圆度误差的公式：•圆度误差（Eccentricity）= 最大测量半径 - 最小测量半径例如，对于一个半径为10mm的圆形对象，经过测量，最大测量半径为，最小测量半径为。
那么该圆形对象的圆度误差为 - (-) = 。
2. 圆度度量计算公式圆度度量指标用来表示一个物体表面曲率变化的平均程度。
以下是计算圆度度量的常用公式：•圆度度量（Roundness）= (Rmax - Rmin) / (Rmax + Rmin) 其中，Rmax表示最大测量半径，Rmin表示最小测量半径。
例如，对于一个圆形对象，最大测量半径为，最小测量半径为。
那么该圆形对象的圆度度量为( - ) / ( + ) = 。
3. 圆的偏心度计算公式圆的偏心度用来衡量一个物体圆心与几何中心的偏离程度。
以下是计算圆的偏心度的公式：•圆的偏心度（Eccentricity）= (Dmax - Dmin) / Dmax 其中，Dmax表示最大直径，Dmin表示最小直径。
例如，对于一个圆形对象，最大直径为20mm，最小直径为19mm。
那么该圆形对象的偏心度为(20mm - 19mm) / 20mm = 。
4. 圆度指数计算公式圆度指数是综合考虑圆度度量和圆的偏心度来评估一个物体圆形度的综合指标。
以下是计算圆度指数的公式：•圆度指数（CIR）= 圆度度量× 圆的偏心度例如，对于一个圆形对象，圆度度量为，偏心度为。
那么该圆形对象的圆度指数为× = 。
以上是一些常见的圆形度计算公式及其例子。
通过这些公式，我们可以准确评估一个物体的圆形度，从而帮助提高工程质量和精度。
圆度测量回转中心与零件轴线的关系
圆度测量回转中心与零件轴线的关系
圆度测量是工程领域中非常重要的一个概念，它用于评估零件的圆形度和轴向偏差。
在制造和装配过程中，确保零件的圆度和轴向偏差达到规定要求是非常关键的，因为这直接影响到零件的性能和精度。
回转中心是指一个零件旋转时所固定在零件上的一个点，它是零件在旋转过程中的轴心。
而零件轴线则是零件自身的几何轴线。
圆度测量就是用来确定回转中心与零件轴线之间的相对位置关系，以评估零件的圆形度和轴向偏差。
在圆度测量中，通常会使用投影仪、三坐标测量机或者其他精密测量设备来测量零件的圆度和轴向偏差。
通过测量零件在旋转过程中的轮廓变化，可以确定回转中心与零件轴线之间的相对位置关系，并进一步评估零件的圆形度和轴向偏差。
圆度测量对于制造和装配过程中的质量控制非常重要。
如果零件的圆度和轴向偏差超出规定范围，可能会导致零件的装配困难、性能下降甚至失效。
因此，通过圆度测量及时发现并纠正零件的圆度和轴向偏差问题，可以有效提高零件的质量和性能，确保产品的
可靠性和稳定性。
总之，圆度测量是评估零件圆形度和轴向偏差的重要手段，它能够帮助制造和装配过程中的质量控制，并对产品的性能和精度起到关键作用。
通过合理的圆度测量，可以确保零件的圆度和轴向偏差符合规定要求，从而提高产品的质量和可靠性。
圆度和圆柱度的计算方式
圆度和圆柱度的计算方式
在工程和制造领域中，圆度和圆柱度是两个非常重要的概念。
圆度指的是一个物体表面的所有点到该物体的中心点的距离的偏差程度。
圆柱度则是指一个物体表面的所有点到该物体的中央轴线的距离的偏差程度。
在实际生产中，这些偏差可能会影响到一个零件的质量和精度，因此需要对圆度和圆柱度进行精确的计算。
计算圆度时，需要测量出该物体在不同的方向上的直径，然后取这些直径测量值的平均值作为该物体的平均直径。
然后根据该物体的平均直径和每个点到该物体中心点的距离，可以计算出该物体表面上每个点到该物体中心点的距离的偏差程度。
计算圆柱度时，需要测量该物体表面在不同方向上的直径，并将这些直径测量值的平均值作为该物体的平均直径。
然后根据该物体的平均直径和每个点到该物体中央轴线的距离，可以计算出该物体表面上每个点到该物体中央轴线的距离的偏差程度。
在进行圆度和圆柱度的计算时，需要使用精密的测量工具，如千分尺、高精度显微镜等。
此外，还需要对测量结果进行统计分析和处理，以确保测量精度和计算准确性。
- 1 -。
圆度、位置度、同心度的测量方法
圆度、位置度、同心度的测量方法1.引言引言部分的内容可以写成以下形式：1.1 概述圆度、位置度和同心度是在工程和制造领域中常用的测量参数，用来评估零部件的质量和符合性。
圆度测量是用来表征一个物体表面的圆柱度或球面度，它是指物体表面与其理想圆柱或球面之间的最大偏离程度。
位置度测量是用来评估物体表面上特定几何要素的位置精度，侧重于表征各个特征之间的相对位置关系。
同心度测量是用来评估物体几何要素的同心性，即各个特征之间所存在的相对偏心程度。
本文将重点介绍圆度、位置度和同心度的测量方法。
首先将介绍圆度的测量方法，包括轮廓法和平面法。
其次将介绍位置度的测量方法，包括坐标法和全距法。
最后将介绍同心度的测量方法，包括中心法和偏心法。
通过详细介绍这些方法，读者将能够了解它们的原理、适用范围和操作步骤，以及它们在实际应用中的优缺点。
本文的目的是为读者提供关于圆度、位置度和同心度测量方法的详细介绍和理解，以便能够正确选择和应用适合的测量方法。
在结论部分，将对这些测量方法的适用性和限制进行讨论，以便读者能够在实际应用中考虑到不同因素和局限性。
通过深入研究和了解这些测量方法，读者将能够更好地评估和控制零部件的质量特性，提高产品的性能和可靠性。
1.2 文章结构本文将从以下几个方面展开对圆度、位置度和同心度的测量方法进行探讨。
首先，在1.1概述中，我们将简要介绍圆度、位置度和同心度的定义和重要性，为后续的测量方法提供背景知识。
其次，在1.2文章结构部分，我们将详细介绍整篇文章的结构安排，包括各个章节的内容与安排。
最后，在1.3目的中，我们将明确本文的目标和研究意义，以期为读者提供清晰的导读。
文章的正文部分将分为三个章节，分别是圆度的测量方法、位置度的测量方法和同心度的测量方法。
在2.1圆度的测量方法部分，我们将重点介绍轮廓法和平面法两种常见的测量方法，分析其原理和适用情况，并对其优缺点进行评述。
在2.2位置度的测量方法部分，我们将着重介绍坐标法和全距法两种常用的测量方法，探讨其测量原理和应用范围，并对其适用性进行讨论。
圆形度计算公式范文
圆形度计算公式范文圆形度是指一个实际对象的形状接近于一个圆的程度。
在工程领域中，常常需要对物体进行圆形度的测量和评估，以确保产品的质量。
圆形度的计算公式可以通过几种不同的方法来确定，下面介绍两种常用的方法。
一、通过圆度偏差公式计算圆形度：圆度偏差是指一个实际圆形与其所在圆心和半径确定的理论圆形之间的最大距离差。
圆度偏差公式可以用以下方式表示：GD&T中RFS的标识方法：中值符号T表示直径与公差的极限，R表示直径的实际尺寸，4R表示圆度的公差。
圆度公差的公式如下：圆度=Σ（每个样品上测得的每个点与圆曲线之间的距离差）/最大圆度测量点数圆度的计算需要根据具体测量样本和仪器进行，通常需要使用三点法进行测量，即随机选取样本上的三个点，测量它们到圆曲线的距离差，并取三者之和作为圆度，然后将所有样本的圆度平均得到最终的圆度值。
之后将得到的圆度值与圆度的公差进行比较，即可评估该样本的圆形度。
二、利用离散点法计算圆形度：离散点法是通过对实际圆形进行多个点的测量，然后通过计算这些点与理论圆心和半径确定的理论圆形之间的最大距离差来确定圆形度。
计算公式如下：圆形度=（Δrma x/ r）×100%其中，Δrmax表示测得的离散点与圆心和半径确定的理论圆形之间的最大距离差，r表示理论圆形的半径。
离散点法的步骤如下：1.确定需要测量的圆形样本。
2.在该样本上选择若干个点进行测量。
3.将测得的点与圆心和半径确定的圆形进行对比，得到距离差。
4.计算所有测量点的距离差的最大值。
5.根据距离差的最大值和理论圆形的半径计算圆形度。
需要注意的是，不同的测量方法和工具可能会得到不同的圆形度计算结果，因此在实际应用中需要根据具体要求和情况选择合适的计算方法。
圆度仪说明书
1.参数和定义参考参考圆是用某种规则匹配测量数据得到的相关圆，据此参考圆计算得到圆度的有关参数。
最小二乘参考圆(LSCI)计算得到的最小二乘参考圆与其内外数据差值的平方和最小。
该圆普遍被用作参考圆。
P=最高峰值V=最低谷值计算得到的最小区域参考圆是两个完全包容测量数据的同心圆，这两圆之间的径向间距最小。
P=最高峰值V=最低谷值最小外接参考圆(MCCI)计算得到的最小外接参考圆是完全将测量数据包容在内的最小圆。
V=圆度计算得到的最大内切参考圆是完全被测量数据包容在内的最大圆。
P=圆度倾斜纠正当测量的圆柱轴线建立后，当它与主轴轴线不平行时，它与主轴轴线在空间某个方向的倾斜将使测量数据发生椭圆畸变。
本选项允许在相对于圆柱轴线进行进一步计算之前，从单个圆度测量数据中去除该椭圆度。
偏心度E偏心值是所选基准轴(点)到所分析参考圆中心的距离。
偏心角为主轴零度位置与参考圆中心和基准轴连线之间的夹角。
A=基准点B=数据中心E=偏心值θ=偏心角(上图为315˚)角度偏心角为主轴零度位置与参考圆中心和基准轴连线之间的夹角。
A=最小二乘中心B=最小二乘参考圆C=角度θE=偏心D=回转中心跳动两个同心圆的径向间隔，这两个圆与基准轴(或点)同心，并完全包容测量数据，即指示器读数的总变动量。
(ISO1101;DIN7184;BS.308第三部分)。
A=跳动B=距基准点最近的数据点C=基准点D=距基准点最远的数据点半径R此值取决于径向横臂的标定(为标尺的目视读数)，仅供参考。
谐波分析数据用傅立叶级数表示。
删除点为从任何间断数据的两边删除的点的个数。
它们是从所选数据总数中删除的。
平面度平面度可用最小二乘或最小区域方法来定义。
最小二乘基准拟合一平面，测量数据至该平面差值的平方和最小。
最小区域基准拟合两个平行平面，使其完全包容测量数据，且间隔最小。
A=轴线F=平面度LS=最小二乘基准“参考平面垂直度”值是两个平行平面最小轴向间隔，这两个平面垂直于参考轴线，并且完全包容由被测数据拟合的最小二乘平面。
定子内径圆度计算公式
定子内径圆度计算公式定子内径圆度是评价定子质量的重要指标之一，它直接影响了电机的运行效率和性能。
定子内径圆度的计算公式是电机行业中的重要知识点，下面我们将深入探讨定子内径圆度的计算公式及其影响因素。
定子内径圆度计算公式可以用以下公式表示：圆度 = (最大内径最小内径) / 平均内径。
其中，最大内径是定子内径的最大值，最小内径是定子内径的最小值，平均内径是定子内径的平均值。
定子内径圆度计算公式的意义在于通过测量定子内径的最大值和最小值，来评估定子内径的圆度程度。
圆度越高，定子内径的偏差就越小，电机运行时的摩擦和振动也就越小，从而提高了电机的运行效率和性能。
定子内径圆度的影响因素主要包括以下几点：1. 加工精度，定子内径的加工精度直接影响了定子内径的圆度。
如果加工精度不高，定子内径就会出现不规则形状，导致圆度较差。
2. 材料质量，定子内径的材料质量也会影响其圆度。
如果材料质量不均匀或存在缺陷，定子内径就会出现不规则形状，导致圆度较差。
3. 加工工艺，加工工艺对定子内径的圆度也有一定影响。
如果加工工艺不当，定子内径就会出现不规则形状，导致圆度较差。
4. 使用环境，定子内径在使用过程中受到的环境影响也会对其圆度产生影响。
如果使用环境恶劣，定子内径就会出现不规则形状，导致圆度较差。
为了保证定子内径的圆度达到要求，需要采取以下措施：1. 严格控制加工精度，确保定子内径的加工精度达到要求。
2. 选择优质的材料，确保定子内径的材料质量均匀，避免出现不规则形状。
3. 优化加工工艺，确保定子内径的加工工艺合理，避免出现不规则形状。
4. 加强使用环境管理，确保定子内径在使用过程中受到良好的环境保护。
通过以上措施的实施，可以有效提高定子内径的圆度，从而提高电机的运行效率和性能。
除了定子内径圆度计算公式和影响因素，我们还需要了解定子内径圆度的检测方法。
常用的定子内径圆度检测方法包括：1. 三点测量法，利用三个测量点对定子内径进行测量，计算出定子内径的最大值、最小值和平均值，从而得出定子内径的圆度。
圆度定义和表示方式
圆度定义和表示方式
圆度是指圆形物体的圆形程度或圆形度量。
在工程和制造领域中，圆度是一个重要的尺寸要求指标，用于评估和描述圆形物体的几何形状特征。
圆度定义为圆形物体最外侧表面与其最内侧表面之间距离的变化，即圆形物体的周长与直径之间的差异。
圆度越高，则圆形物体的形状越接近完美的圆形。
表示圆度的方式有很多种，以下是几种常见的表示方法：
1. 圆度公差：圆度公差是描述圆形物体形状偏差的一种方式。
通常使用直径公差的一半来表示圆度公差。
例如，如果一个圆形物体的直径公差为±0.02mm，那么它的圆度公差为±0.01mm。
2. 圆度图：圆度图是用来直观地表示圆度的一种图形方法。
通过在图中绘制圆形物体的内外轮廓线，可以清晰地展示圆度是否达到要求。
3. 圆度测量仪器：测量仪器可以用来测量圆形物体的实际圆度。
常见的圆度测量仪器有圆度仪和投影仪等。
这些仪器可以精确地测量圆形物体的直径差异，并计算出圆度值。
圆度的概念和表示方式在工程制造领域中具有重要意义。
圆度的要求对于一些精密产品的制造非常关键，例如轴承、齿轮等。
只有具备良好的圆度，才能确保产品的正常运转和高精度的工作效果。
总之，圆度定义了圆形物体的圆形程度，表示方式包括圆度公差、圆度图和圆度测量仪器等。
圆度的要求对于精密工程制造非常重要，它是评估和描述圆形物体几何形状特征的重要指标。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
定义
圆度：是指工件的横截面接近理论圆的程度。
测量工具为圆度仪。
地质学名词：圆度（roundness）又称磨圆度（psephicity），是指岩石或矿物颗粒在搬运过程中，经流水冲刷，互相撞击之后，棱角被磨圆的程度。
颗粒棱角越多越尖锐则圆度越差；反之棱角圆滑，圆度就好。
碎屑颗粒圆度可用公式P=Σr/N·R计算求出。
式中Σr=r1+r2+r3……+rn为颗粒各角的曲率颗粒最大投影面上圆度的测量半径总和，R为该颗粒轮廓内最大内接圆半径，N为所测角的曲率半径的数目。
卢赛尔等（1937年）曾分出五种颗粒类型：棱角状、次棱角状、次圆状、圆状、极圆状，并提出相应的圆度数值。
当对碎屑沉积物的圆度作整体分析时，要求出所有碎屑的平均圆度，这时，可统计各类圆度等级的颗粒数按加权平均法求其平均圆度即可。
主要功能
可快速测环形工件的圆度、表面波纹度（Wc、Wp、Wv、Wt、Wa、Wq、Swm）、谱分析、波高分析、、同心度、垂直度、同轴度、平行度、平面度、轴弯曲度、偏心、跳动量等。
测量仪器
测量仪器很多，然而使用不同仪器会产生不同测量误差。
本文介绍了用光学分度头测量圆度误差时所建立的数学模型，分析了各种误差对测量误差的影响，从而为在保证测量精度的同时降低测量成本提供了理论依据。
圆度误差的测量
测量方法
圆度误差的评定方法有4种：最小包容区域法，最小外接圆法，最大内切圆法，最小二乘法。
由于最小二乘法简便易行，长期以来甚为流行。
测量圆度误差的方法虽有多种，但最为合理、用得最多的是半径法。
为此，通过采用半径测量法在光学分度头上用千分表测量圆度误差，并对测量数据进行最小二乘法计算，以求得圆度误差值。
测量时，将被测量工件顶在光学分度头的两顶尖间，将指示表置于被测量横截面上，测量其半径的变化量Δr，即利用光学分度头将被测圆周等分成n个测量点，当每转过一个θ=360°/n角时，从指示表上读出该点相对于某一半径R0的偏差值Δr，由此测得所有数据Δri。
建立数学模型
见图1，若实际被测表面的位置用极坐标(ri，θi)来表示，则ri=ecos(θi-α)+[(R+Δri)2-e2sin(θi-α)]1/2。
．．．．．．．．．．(1)
式中：i－－测点数，i=1，2，……，n Δri－－半径偏差观察值；e－－最小二乘圆圆心O1(a,b)的偏移量，a=ecosα,b=esinα。
由于圆度误差精度测量的特点，在测量之前必须调整零件的回转轴线，使a,b之值较小，满足“小偏差假设”，并且零件的圆度误差和其半径相比是微量，称为“小误差情况”，于是式(1)近似为ri=e(θi-α)+R+Δri，因此根据最小二乘法原理有E2=∑ni=1Δr2i=∑ni=1〔ri-R-ecos(θi-α)〕2=min。
(2)
根据?э(E2)/эR=0，э(E2)/эe=0，э(E2)/эα=0，可得∑ni=1ri-nR-e∑ni=1cos(θi-α)=0
∑ni=1ricos(θi-α)-R∑ni=1cos(θi-α)-e∑ni=1cos2(θi-α)=0 ．．．．(3) ∑ni=1risin(θi-α)-R∑ni=1sin(θi-α)-e∑ni=1cos(θi-α)sin(θi-α)=0。
如果各测点均布圆周，且n充分大，则
∑ni=1cos(θi-α)=0,∑ni=1sin(θi-α)=0,
∑ni=1cos2(θi-α)=n/2,∑ni=1sin2(θi-α)=n/2,
∑ni=1cos(θi-α)sin(θi-α)=0,
经简化计算，式(3)的解为
a=2/n∑ni=1Δricosθi
b=2n∑ni=1Δrisinθi
Δr=1/n∑ni=1Δri
R=R0+Δr。
．．．．．．．．．．．．．．．．．．．．．．．．．．．(4)
于是，被测圆上各点到最小二乘圆之径向距离为εi=Δri-Δr-acosθi-bsinθi，则圆度误差为Δf0=εmax-εmin。
误差分析
量仪的回转精度引起的误差回转轴线在回转过程中，对轴线平均位置的相对位移即为回转误差运动。
误差运动使回转轴在每一瞬时发生轴向窜动和径向跳动，
使被测工件一转内的采样点不全在一个横截面内，从而使各采样点间的相关性降低。
但是，由于轴向窜动一般很小，而实际工件被测表面是平滑的，测头在被测表面采样时，也不可能是纯粹的点接触，而是小面积接触，因此轴向窜动对测量精度的影响可以忽略。
径向跳动误差将直接传递到采样数据Δri中，进而影响最小二乘圆心坐标的计算精度。
由式(4)可得〔2〕da=db<2d√nd(Δrmax)。
因此，径线回转精度是圆度误差测量中极为重要的精度指标。
对于光学分度头，是用顶尖装夹工件，其回转精度则由顶尖精度和被测工件顶尖孔的形状精度共同决定。
偏心e引起的误差由于测量时的回转中心O与最小二乘圆的圆心O1不重合，存在偏心e=OO1，式(2)中Δri=ri-R-ecos(θi-α)是式(1)用R+Δri代替[(R+Δri)2-e2sin2(θi-α)]1/2(其中α=arctgb/a)得到的，所以e引起的误差为δe=R+Δri-[(R+Δri)2-e2sin2(θi-α)]1/2，把上式展开成Talor级数得δe=e2/2(R+Δri)sin2(θi-α)，因sin2(θi-α)≤1,且R+Δri≈ri，则δemax=e2/2ri。
由于e是微米级，ri是毫米级，所以此项误差一般很小，可忽略。
测头安装误差测头安装误差示意见图2。
当测头的位置不通过被测工件的轴线而偏离距离为Δ时，则相应的偏离角为：θ=arcsinΔR，若被测表面半径有增量Δr 时，测头的实际位移为AB，其测量误差δθ=AB-Δr，因为Δr，AB<<R,∠ABO≈θ，则Δr=ABcos∠ABO≈ABcosθ，所以δθ≈Δrcosθ-Δr=(1/cosθ-1)=2sin2θ/2Δr。
由于θ角很小，用θ弧度值代替sin(θ/2)得δθ=AB-Δr≈2sin2(θ/2)Δr=θ2/2Δr。
因此，测头安装误差很关键，尤其在测小直径时必须注意测头位置。
通常应使θ≤10°，即e/R≤0.15，此时δθ≤2%。
测点数对测量误差的影响由于在轮廊上实测有限数量的点来代替被测实际轮廊的全貌，在原理上就存在了误差。
为了减少此误差，应合理选择测点数。
用计算机对圆度谐波进行模拟，利用数值积分可以求出对应于一定谐波时各种测点的不确定度，随测点数增加，测量不确定度下降。
结论
综上所述，用最小二乘法计算圆度误差，采用分度头测量时，仪器的回转精度、测头的安装误差及测点数是产生测量误差的主要因素。
应尽量设法减少其影响，从而提高测量精度。