SPSS 比较均值 独立样本T检验 案例分析
SPSS06均值比较与T检验

例子:
检验男女雇员现工资是否有显著性差异。 分析变量的简单描述统计 G r o up S量 i st i c s tat
Current Salary Gender Female Male N 216 258 Mean $26031.92 $41441.78 Std. Deviation $7,558.02 $19,499.21 Std. Error Mean $514.26 $1,213.97
Current Salary
Equal variances assumed Equal variances not assumed
F 119.669
Sig. .000
t -10.945 -11.688
df 472 344.262
有29名13岁男生的身高、体重、肺活量数据。试分析身高大 于等于155厘米的与身高小于155厘米的两组男生的体重和肺 活量均值是否有显著性差异。data06-03数据 分组描述统计量
12岁男孩身高
t 1.032
df 119
T检验:
x 0 t sx
Max(v1 , v 2 ) F Min(v1 , v 2 )
,
方差齐性检验:
方差齐时使用公式 :
t Sc
x1 x2 1 1 n1 n2
Sc是合并方差 :
Sc
( x1 x1 ) 2 ( x2 x2 ) 2 n1 n2 2
身高 年龄 10 11 12 13 Total Mean 1.4488 1.5209 1.6129 1.5900 1.5259 N 8 11 7 1 27
N 13 14 27
a
b
相同年龄的男孩和女孩是否身高有所不同?是否身 高随年龄的增长呈线性关系?如果解决这样的问题, 只建立一个控制层就不够了。应该考虑,选择身高h 作为因变量,分类变量age作为第一层控制变量,sex 为第二层控制变量。两个分类变量分别放在两层中, 且使用选择项。
SPSS数据处理小结:T检验、相关、二分类、散点图、箱图
我们首首先来看一一个表格:
!!!
图6
这个表格一一般是流行行病学调研类文文章必备的表格了,上面面分为了“control”组 和“PCOS”组(不用用去管它是什么意思……)和后面面的P value,然后最下面面有 写明,数据除非非有特殊说明,都是用用均值±标准差的形式来表示示的。 需要特殊说明的是,一一般情况下,两组数据有统计学上的差异,就是后面面的 那个P值要小小于0.05~当然我们会看到“<0.01”的情况,那样表示示数据差异非非
在曲线的两侧,得分就高高。然
后我们还要关注的就是参数估
计值了,有一一个常数为1.203
和b1为0.151,而而我们的方方程
!!线性的,即:y=0.151*x +1.203
2.分析→相关→双变量
!
!图!!!!!!!!!!! 2-‐1
3.进入入之后选择要分析的两组数据:IR和年龄,pearson:矩阵相关系数,
参数方方法(属于系统默认方方法),剩下的两个均为非非参数方方法,自自行行补脑使
!! 用用。然后下面面的双侧(尾)检验也是系统默认的。
图!!!!!!!!!!! 2-‐2
!一.均值比较
(一).单样本t检验(one sample t test)
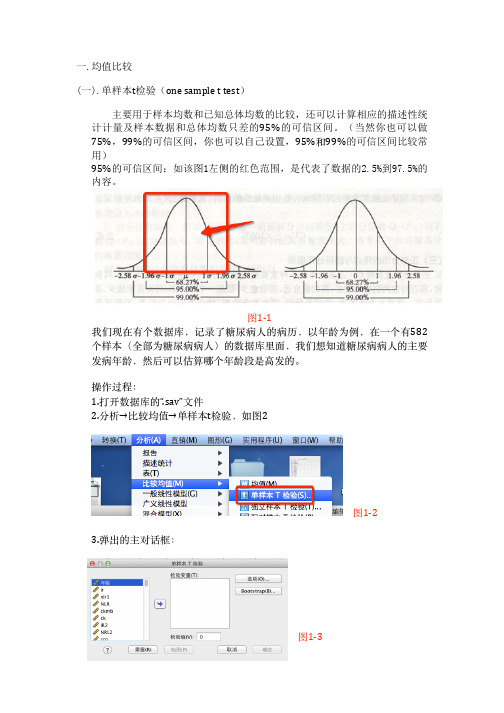
主要用于样本均数和已知总体均数的比较,还可以计算相应的描述性统 计计量及样本数据和总体均数只差的95%的可信区间。(当然你也可以做 75%,99%的可信区间,你也可以自己设置,95%和99%的可信区间比较常 用) 95%的可信区间:如该图1左侧的红色范围,是代表了数据的2.5%到97.5%的 内容。
! 图1-‐8 图1-‐9
的数值,就是均值差值(Mean Difference),首首先均值差值是否在95%的可
spss独立样本T检验

例题
比较两批电子器材的电阻,随机抽取的样本测量电阻如题表2所示,试比较两批电子器材的电阻是否相同?(提示:需考虑方差齐性问题)
分析步骤:
单击工具栏“分析”——>单击“比较均值”——>单击“单因素ANOVA检验”——>因变量列表置为电阻——>因子置为类别——>选项——>选中方差齐性检验
图1 单因素ANOVA检验
图2 统计
单击工具栏“分析”——>单击“比较均值”——>单击“独立样本T检验”——>检验变量置为电阻——>单击定义组——>填入A批、B批——>单击“确定”
图3 独立样本T检验结果展示:
表4:独立样本检验
结果分析:
假设A,B两批电阻相互独立且均服从正态分布。
H0:u1-u2=0,两批电阻器材的电阻相同
H1:u1-u2≠0,两批电阻器材的电阻不相同
1、查看表4莱文方差等同性检验(levene),假定等方差(显著性为0.435>0.05,代表方差是齐性的),我们看第一行数据。
t检验结果显示,t=1.648,v=12,P=0.125>0.05,按照检验水准,接受H0,拒绝H1,故两批电阻器材的电阻相同。
2、查看表4莱文方差等同性检验(levene),不假定等方差,我们看第二行数据。
t’检验结果显示,t=1.648,v=10.671,P=0.129>0.05,按照检验水准,接受H0,拒绝H1,故两批电阻器材的电阻相同。
spss操作独立样本T检验模板
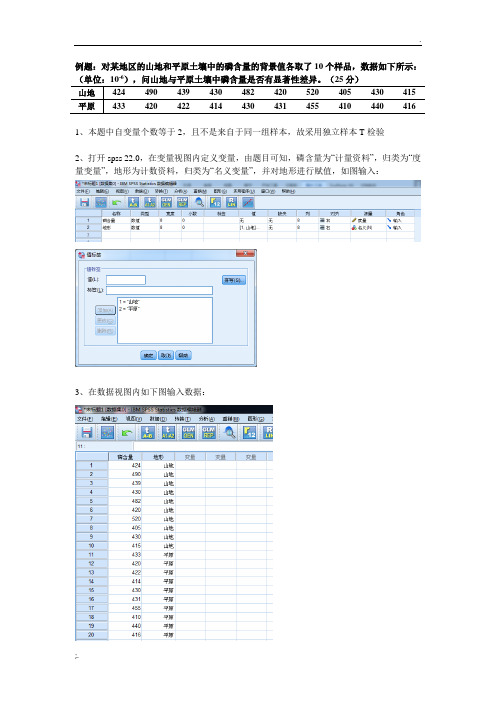
例题:对某地区的山地和平原土壤中的磷含量的背景值各取了10个样品,数据如下所示:-6山地424 490 439 430 482 420 520 405 430 415 平原433 420 422 414 430 431 455 410 440 4161、本题中自变量个数等于2,且不是来自于同一组样本,故采用独立样本T检验2、打开spss 22.0,在变量视图内定义变量,由题目可知,磷含量为“计量资料”,归类为“度量变量”,地形为计数资料,归类为“名义变量”,并对地形进行赋值,如图输入:3、在数据视图内如下图输入数据:4、独立样本T检验进行的假设:(1)数据必须为连续性数据;(2)方差齐性(可偏不齐,即σ12/σ22<3);(3)每组数据均服从正态分布5、进行验证:(1)由题目可以看出,数据为连续型数据,满足;(2)此检验可于结果中查看;(3)首先,新建spss视图,重新输入变量进行探索队列,如下图所示:将“山地”“平原”选入因变量列表,并于“绘图(T)”中勾选“带检验的正态图”,操作步骤如下图所示:根据正态性检验表的“K-S检验”结果,由于样本内数据数量<30,故看Shapiro-Wilk结果,由于两者的sig均大于0.05,故满足正态分布正态性检验Kolmogorov-Smirnov(K)a Shapiro-Wilk统计df 显著性统计df 显著性山地.268 10 .041 .856 10 .069平原.146 10 .200*.945 10 .608*. 这是真正显著性的下限。
a. Lilliefors 显著性校正6、进行独立样本T检验:(1)依次点击“分析”-“比较平均值”-“独立样本T检验”,调出独立样本T检验对话框:(2)将“磷含量”选入检验变量(T),将“地形”选入分组变量,然后定义组,于主页面中点击“确定”,输出结果:组统计地形数字平均值(E) 标准偏差标准误差平均值磷含量山地10 445.50 38.106 12.050 平原10 427.10 13.609 4.304独立样本检验列文方差相等性检验平均值相等性的t 检验F 显著性t自由度显著性(双尾)平均差标准误差差值差值的95%置信区间下限上限磷含量已假设方差齐性9.559 .006 1.438 18 .168 18.400 12.796 -8.482 45.282未假设方差齐性1.438 11.259 .178 18.400 12.796 -9.684 46.484根据独立样本检验表的方差方程的Levene检验,F统计量的sig值0.006<0.05,否认方差相等的假设,认为方差不齐性,故参考第二行的t检验结果;第二行t检验的双侧sig=0.178>0.05,即可认为在0.05的显著性水平上,山地与平原土壤中磷含量是否没有有显著性差异。
SPSS课件第四章 均值比较与T检验

辽宁医学院
SPSS统计软件应用
温有锋
进行均值比较及检验的过程
MEANS 过程 T test 过程 单一样本T检验 独立样本的T检验
配对样本的T检验
单因素方差分析
辽宁医学院
SPSS统计软件应用
温有锋
一、定量资料基本分析过程(MEANS过程)
MEANS过程用于定量资料的统计分析,可
计算21种统计量,还可以进行单向方差分析。 当观测量按一个分类变量分组时,MEANS过 程可以进行分组计算。例如要计算学生的平 均身高,SEX变量把学生按性别分为男、女
CHILD.sav数据文件在SP11DATA文件夹下
辽宁医学院
SPSS统计软件应用
温有锋
练习题
在治疗肝癌的药物研究中,为了提高治疗药物在靶器官— 肝脏的浓度,降低在非靶器官如心脏的浓度,行2×3×2 析因设计,即设置3个因素,第一个因素是药物 (“drug”),有2个水平,分别为“丝裂酶素+高分子物 质+磁性物质”(实验组=1)和“丝裂酶素”(对照组 =2);第二个因素是时间(“time”),有3个水平,分别 为给药后15min(=1)、30min(=2)和60min(=3);第 三个因素器官(“organ”),有2个水平,分别是心脏 (=1)和肝脏(=2)。将60只小鼠随机分为12组(即 2*3*2种组合),每组5只,即重复的例数为5。观察指标 (反应变量)为组织中丝裂酶素的浓度(ug/g),结果见 表8-1和数据文件“factorial_1”。
差别等也会造成一定的偏差,使样本统计量SS统计软件应用
温有锋
均值比较的概念
由此可以得出这样的认识:
均值不相等的两个样本不一定来自均值不同
的总体。 能否用样本均数估计总体均数,两个变量均 数接近的样本是否来自均值相同的总体?换 句话说,两个样本某变量均值不同,其差异 是否具有统计意义,能否说明总体差异?这 是各种研究工作中经常提出的问题。这就要 进行均值比较。
spss均值检验(均数分析单样本t检验独立样本t检验)

在统计学中,我们往往从样本的特性推知随机变量总体的特性。
但由于总体中个体之间存在差异,样本的统计量和总体的参数之间往往会有误差。
因此,均值不相等的样本未必来自不同分布的总体,而均值相等的样本未必来自有相同分布的总体。
也就是说,如何从样本均值的差异推知总体的差异,这就是均值比较的内容。
SPSS提供了均值比较过程,在主菜单栏单击“Analyze”菜单下的“Compare Means”项,该项下有5个过程,如图4-1。
平均数比较Means过程用于统计分组变量的的基本统计量。
这些基本统计量包括:均值(Mean)、标准差(Standard Deviation)、观察量数目(Number of Cases)、方差(Variance)。
Means过程还可以列出方差表和线性检验结果。
[例子]调查了棉铃虫百株卵量在暴雨前后的数量变化,统计暴雨前和暴雨后的统计量,其数据如下:暴雨前 110 115 133 133 128 108 110 110 140 104 160 120 120暴雨后 90 116 101 131 110 88 92 104 126 86 114 88 112该数据保存在“DATA4-1.SAV”文件中。
1)准备分析数据在数据编辑窗口输入分析的数据,如图4-2所示。
或者打开需要分析的数据文件“DATA4-1.SAV”。
图4-2 数据窗口2)启动分析过程在SPSS主菜单中依次选择“Analyze→Compare Means→Means”。
出现对话框如图4-3。
图4-3 Means设置窗口3)设置分析变量从左边的变量列表中选中“百株卵量”变量后,点击变量选择右拉按钮,该变量就进入到因子变量列表“Dependent List:”框里,用户可以从左边变量列表里选择一个或多个变量进行统计。
从左边的变量列表中选中“调查时候”变量,点击“Independent List”框左边的右拉按钮,该变量就进入分组变量“IndependentList”框里,用户可以从左边变量列表里选择一个或多个分组变量。
spss 均值的比较与检验

三、应用举例
例5-5-1,某轮胎厂的质量分析报告中说明,该厂某轮胎的平均寿命在 一定的载重负荷与正常行驶条件下会大于25000公里。平均轮胎寿命的公里数 近似服从正态分布。现对该厂该种轮胎抽出一容量为15的样本,试验结果得样 本均值为27000公里。能否做出结论:该厂产品与申报的质量标准相符?数据 如下(e5-5-2.sav)
z ~ t (n 1) sz / n
在显著水平α下, 双侧检验的H0拒绝区域为: | t | t (n 1)
2
二、配对样本T检验功能与应用
配对样本T检验是进行配对样本均数的比较。执行该过程, SPSS显示:
每个变量的均数、标准差、标准误和样本含量;
每对变量的相关系数;
每对变量的均数的差值、差值的标准误和可信区间; 检验每对变量均数的差值是否来自总体均数为0 的t检验结果。 三、应用举例 例5-5-4 :(e5-5-5.sav)
设总体X服从正态分布N(μ,σ2),其中σ2未知。从中抽出子样 (x1,x2,…,xn),现要检验假设H0: μ= μ0,H1: μ≠ μ0,其中μ0为已知 常数。 x μ0 其中S为子样标准差。 通常σ是未知: T
s / n 1
若H0成立,则统计量T服从自由度为n-1的t分布。对于给定的α, 由t分布表可查得临界值t α/2(n-1), 使 P{|T|>t α/2(n-1)}= α 如果算得T的值t落入其拒绝域|t|>t α/2(n-1)内,则拒绝H0;否则 不能拒绝H0。 二、单样本T检验的功能与应用
SPSS生物统计分析示例2-2样本t检验

SPSS统计分析示例
例二:
将20名某病患者随机分为两组,分别用甲乙两药治疗,测得治疗前后的血沉(mm/小时)如下表:
试分甲乙两药是否有疗效?两药疗效是否有差异?并用图或表对数据和结果进行描述。
1.对两种药物治疗效果比较的统计分析
(以下结果均使用SPSS统计软件获得)
(1)对甲药疗效做配对t检验:
治疗前后血沉值的差值的配对检验SPSS结果显示:t=5.237(df=9),单侧检验P=0.001x2<0.01,结论甲药疗效极显著。
(2)对乙药疗效做配对t检验:
治疗前后血沉值的差值的配对检验SPSS结果显示:t=5.303(df=9),单侧检验P<<0.01,结论乙药疗效极显著。
(3)对甲药、乙药的疗效做独立双样本的t-检验
由SPSS输出表可知:甲药、乙药给药后血沉差值样本数据满足方差齐性要求,t=-1.602(df=18),双侧检验P=0.127>0.05,则两种药的疗效无显著差异。
汇总表
服药前服药后差值t
甲药mm/h (M±SD) 8.7±2.4 5.5±3.1 3.2±1.9 5.237**
乙药mm/h (M±SD) 9.6±1.8 4.6±2.0 5.0±3.0 5.303**
甲药与乙药比较 1.602 **:P<0.01。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
SPSS-比较均值-独立样本T检验案例解析
2011-08-26 14:55
在使用SPSS进行单样本T检验时,很多人都会问,如果数据不符合正太分布,那还能够进行T检验吗?而大样本,我们一般会认为它是符合正太分布的,在鈡型图看来,正太分布,基本左右是对称的,一般具备两个参数,数学期望和标准方差,即:N(p, Q)
如果你的样本数非常少,一般需要进行正太分布检验,检验的方法网上很多,我就不说了
下面以“雄性老鼠和雌性老鼠分别注射了某种毒素,经过观察分析,进行随机取样,查看最终老鼠是否活着。
问题:很多人认为,雄性老鼠和雌性老鼠分别注射毒液后,雌性老鼠存活下来的数量会比雄性老鼠多?
我们将通过进行统计分析来认证这个假设是否成立。
下面进行参数设置:a 代表:雄性老鼠
b代表:雌性老鼠
tim 代表:生存时间,即指经过多长时间后,去查看结果
0 代表:结果死亡
1 代表:结果活着
随机抽取的样本,如下所示:
打开SPSS- 分析---检验均值---独立样本T检验,如下图所示:
将你要分析的变量,移入右边的框内,再将你要进行分组的变量移入“分组变量”框内,“组别group()里面的两个参数,不能够随意设置,必须要跟样本里面的数字一致
点击确定后,分析结果,如下所示:
从组统计量可以看出,雄性老鼠的存活下来的均值为0.73,但是雌性老鼠存活下来的均值为1.00,很明显,雌性老是存活下来的个数明显比雄性老鼠多,但是一般我们不看这个结果,为什么?因为样本不够大,如果将样本升至10000个?也许这个均值将会发生变化,不具备统计学意义,
我们一般只看独立样本检验的结果。
独立样本检验,提供了两种方法:levene检验和均值T检验两种方法
Levene检验主要用来检验原假设条件是否成立,(即:假设方差相等和方差不相等两种情况)如果SIG>0.05,证明假设成立,不能够拒绝原假设,如果
SIG<0.05,证明假设不成立,拒绝原假设。
进行levene检验结果判断是第一步,从上图,可以看出 sig<0.05 方差相等的假设不成立,所以看第二行,方差不相等的情况
sig=0.082>0.05 即说明 P 值大于显著性水平,不应该拒绝原假设:即指:雌性老鼠和雄性老鼠在注射毒液后,存活下来的个数没有显著的差异
本次分析的结果,不支持,很多人认为的:雄性老鼠和雌性老鼠分别注射毒液后,雌性老鼠存活下来的数量会比雄性老鼠多的结论。
其实方差不相等,并不代表不符合正太分布,也不能够说有显著的差异,方差不相同,说明曲线的偏离程度不同而已。
