多段图最短路径_动态规划
动态规划求最短路径的两种方法
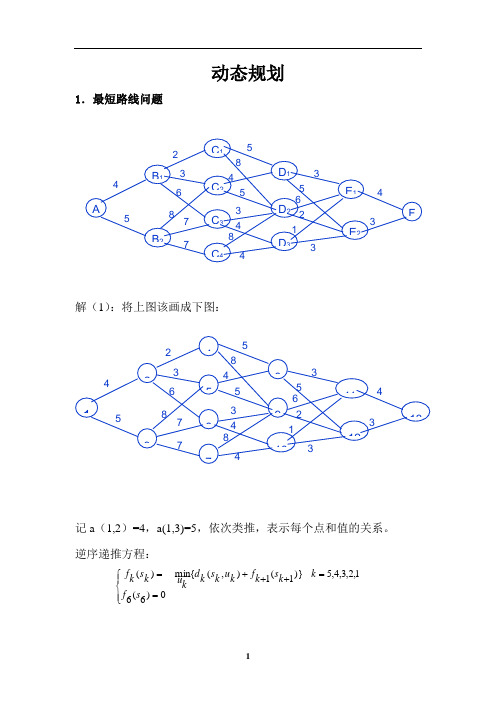
动态规划1．最短路线问题解（1）：将上图该画成下图：记a （1,2）=4，a(1,3)=5，依次类推，表示每个点和值的关系。
逆序递推方程：⎪⎩⎪⎨⎧==+++=0)6(61,2,3,4,5)}1(1),({min )(s f k k s k f k u k s k d k uk s k fAB 1B 2C 1 C 2C 3 C 4D 1D 2 D 3E 1 E 2F4523 6 8 7 75845348435 6 2 314 31234 5 6 789 101112134523 6 8 7 7584534 8435 6 2 314 3如图各状态：逆序递推，找出上一个状态到下一阶段的最小路径值。
例如，当K=4时，状态 它们到F 点需经过中途 点E ，需一一分析从E 到 F 的最短路：先说从D1到F 的最短路 有两种选择：经过 E1, E2, 比较最短。
这说明由 D1 到F 的最短距离为7，其路径为AB 1B 2C 1 C 2C 3 C 4D 1 D 2 D 3E 1 E 2F4523 6 87 75845348435 62 31 4 3第1阶段 第2阶段 第3阶段 第4阶段 第5阶段状态 1状态 2状态3状态 4状态 5状态 6)}(),(),(),(m in{)(252141511414E f E D d E f E D d D f ++=.7}35,43min{=++=.11F E D →→},,{3214D D D S =a=[0,4,5,inf,inf,inf,inf,inf,inf,inf,inf,inf,inf 4,0,inf,2,3,6,inf,inf,inf,inf,inf,inf,inf 5,inf,0,inf,8,7,7,inf,inf,inf,inf,inf,inf inf,2,inf,0,inf,inf,inf,5,8,inf,inf,inf,inf inf,3,8,inf,0,inf,inf,4,5,inf,inf,inf,inf inf,6,7,inf,inf,0,inf,inf,3,4,inf,inf,inf inf,inf,7,inf,inf,inf,0,inf,8,4,inf,inf,inf inf,inf,5,4,inf,inf,inf,0,inf,inf,3,5,inf inf,inf,inf,8,5,3,8,inf,0,inf,6,2,inf inf,inf,inf,inf,inf,4,4,inf,inf,0,1,3,inf inf,inf,inf,inf,inf,inf,inf,3,6,1,0,inf,4 inf,inf,inf,inf,inf,inf,inf,5,2,3,inf,0,3 inf,inf,inf,inf,inf,inf,inf,inf,inf,inf,4,3,0]; s8=min(a(8,11)+a(11,13),a(8,12)+a(12,13)); s9=min(a(9,11)+a(11,13),a(9,12)+a(12,13)); s10=min(a(10,11)+a(11,13),a(10,12)+a(12,13)); s4=min(a(4,8)+s8,a(4,9)+s9); s5=min(a(5,8)+s8,a(5,9)+s9); s6=min(a(6,9)+s9,a(6,10)+s10); s7=min(a(7,9)+s9,a(7,10)+s10); s2=[a(2,4)+s4,a(2,5)+s5,a(2,6)+s6]; s2=min(s2);s3=[a(3,5)+s5,a(3,6)+s6,a(3,7)+s7]; s3=min(s3);s1=min(a(1,2)+s2,a(1,3)+s3)运行结果为：s8 = 7 s9 = 5 s10 = 5 s4 = 12 s5 = 10 s6 = 8 s7 = 9 s2 =13s3 = 15 s1 = 17结果分析：s 表示每个点到终点的最短距离，那么最短路程为17。
动态规划_多段图_最小花费通路算法_C语言
动态规划_多段图_最小花费通路算法_C语言动态规划找出多段图的最小花费通路算法（C语言）//算法：#include#include#define MAX 50#define MAX_LEN 100 /*定义顶点之间最大花费（假设最大花费为100）*///结构体定义typedef struct edgenode{ /*定义边表结点结构体*/int adjvertex; /*邻接点编号*/int len; /*该结点与父结点之间的花费*/struct edgenode *next; /*指向下一个邻接点*/} EdgeNode;typedef struct vertexnode{ /*定义顶点结点结构体*/EdgeNode *firstedge; /*边表头指针*/} VertexNode;typedef struct { /*定义邻接表结构体*/VertexNode adjlist[MAX]; /*邻接表*/int vertexNum; /*顶点数*/int edgeNum; /*边数*/} ALGraph;//函数声明ALGraph * CreateALGraph(int vertexNum, int edgeNum);void MultistageGraph(ALGraph *G, int n, int route[], int *minCost);//主函数int main(){ALGraph *G = NULL;int vertexNum, edgeNum; /*顶点数和边数*/int *route; /*从源点到收点的最短路径上的顶点编号*/int minCost; /*最短路径的最小费用*/int i;printf("请输入顶点数和边数：\n");scanf("%d,%d", &vertexNum,&edgeNum);//初始化GG = CreateALGraph(vertexNum, edgeNum);if(!G){return 0;}//初始化route数组route = (int *)malloc(sizeof(int) * vertexNum);MultistageGraph(G, vertexNum, route, &minCost);//输出最小花费路径及最小花费printf("\n最小花费路径是：\n");for(i = 0; i < vertexNum; i ++){printf("%d —> ", route[i]);if(route[i] == (vertexNum - 1)){printf("\b\b\b\b \n");break;}}printf("\n最小花费是：%d\n", minCost);return 0;}/*********************************************************** 函数名称：GreateALGraph函数功能：初始化有向图的邻接表输入：顶点数ertexNum，边数edgeNum输出：指向已初始化完毕的有向图的邻接表指针***********************************************************/ ALGraph * CreateALGraph(int vertexNum, int edgeNum){ ALGraph *G = NULL;int i, j, u, v, info;G = (ALGraph *)malloc(sizeof(ALGraph));if(G){G->vertexNum = vertexNum;G->edgeNum = edgeNum;for(i = 0; i < vertexNum; i ++) {G->adjlist[i].firstedge = NULL;}//给边表结点分配内存空间printf("请输入分段图中各相邻结点的编号及其权值：\n");for(j = 0; j < edgeNum; j ++) {//初始化边结点EdgeNode *pnode = NULL;pnode = (EdgeNode *)malloc(sizeof(EdgeNode));pnode->next = NULL;//输入相邻结点的编号及其边上的权值scanf("%d,%d,%d", &u, &v, &info);if(pnode){pnode->next = G->adjlist[u].firstedge;G->adjlist[u].firstedge = pnode;pnode->adjvertex = v;pnode->len = info;}else{return NULL;}}}return G;}/***********************************************************函数名称：MultistageGraph函数功能：多段图中利用动态规划找出源点到收点的最小花费通路输入：指向有向图的邻接表指针G，结点个数n，保存最小花费通路结点的数组route，保存最小花费minCost输出：最小花费通路结点的数组route，最小花费minCost***********************************************************/void MultistageGraph(ALGraph *G, int n, int route[], int *minCost){int *cost; /*每个结点到收点的最小费用*/int *path; /*在阶段决策中，各个顶点到收点的最短路径上的前方顶点编号*/int i;//给cost、path、route指针分配n个int大小的内存空间cost = (int *)malloc(sizeof(int) * n);path = (int *)malloc(sizeof(int) * n);//初始化cost、path、route指向的内存空间for(i = 0; i < n; i ++) {cost[i] = MAX_LEN;path[i] = -1;route[i] = 0;}cost[n-1] = 0; /*收点到收点的距离为0*///动态规划过程for(i = i - 2; i >= 0; i --) {EdgeNode *pnode = G->adjlist[i].firstedge;while(pnode && (pnode->len + cost[pnode->adjvertex]) < cost[i]) { cost[i] = pnode->len + cost[pnode->adjvertex];path[i] = pnode->adjvertex;pnode = pnode->next;}}i = 0;while((route[i] != n-1) && (path[i] != -1)) {i ++;route[i] = path[route[i - 1]];}//最小花费*minCost = cost[0];//释放malloc申请的内存空间free(cost);free(path);return;}运行结果：。
动态规划------最短路径问题
动态规划------最短路径问题最短路径问题是动态规划的⼀个实例。
1.最短路径问题的描述2.举个例⼦来说明：求从 S 到 T 的最短路径。
3.思考⽅式4.利⽤动态规划求解问题依次考虑从 C 到 T 的最短距离。
考虑从 B 到 C 的最短距离考虑从 A 到 B 的最短距离考虑从 T 到 A 的最短距离每次都是最短距离。
在整个过程中，我们把我们的⽬标问题转化成了⼀个个的⼦问题，在⼦问题求最⼩值，最后解决了这个问题。
4.⼦问题的界定5.最短路程之间的依赖关系每⼀次计算的时候都是依据前⼀个⼦问题。
不需要⼀个⼀个计算。
每次计算都可以直接利⽤前⼀个问题的解。
6.⼦问题的优化原则6.利⽤动态规划求解是需要条件的，⼀个反例告诉你，动态规划求解的条件分析：假如从S 到 T 经过的节点依次是 A B C ，从C 到 T ，模10，我们选择上⾯的2 . 从 B 到 C，我们的两条路分别是 4 和 7 ，模10，我们选择上⾯的 4 ，那么，从B到T的最短距离就是 6；从 A 到 B ，我们的两条路分别是 6 和 9，模10，我们选择上⾯的路。
从 S 到 A ，两条路分别是 8 和 11，此时，模10，我们选择下⾯的路。
这时，路径就如上图中蓝⾊的路径了。
但是，这是最优的路径吗？显然不是，红⾊的路线才是最优的路径。
因为模10后，得到的结果为0，⽐ 1 ⼩。
为什么是错误的？因为破坏了动态规划的优化原则，它的问题和它的⼦问题的优化函数之间没有依赖关系。
⽐如，我们考虑最后⼀段即 C 到 T的距离，显然， 2是最优解，⽽不是 5 。
因此，破坏了优化原则的问题不能使⽤动态规划。
7.动态规划⼩结可以⽤于求解组合优化问题。
注意动态规划的最优化的原则。
8.代码这个问题的简化版本，编码实现：从矩阵的（0,0）位置到矩阵的（array.length-1,array[0].length-1）的位置的最⼩值。
例：动态规划解最短路径问题：
● 例：动态规划解最短路径问题：步骤(1)、(2)已实现。
最优子结构：从起点到终点的最短路径包含了该路径上各点到终点的最短路径。
递归公式：设v 为图中一个顶点，v 1, v 2,…, v m 为v 的直接后继，cost(v)表示v 到终点的最短路径长度，c[u, w]表示边<u,w>上的权，t 为终点，则cost 满足如下递归公式：⎪⎪⎩⎪⎪⎨⎧≠∞=≠+=≤≤无后继且有后继且v t v , tv , 0v t v , )}cost(v ] v {c[v,min cost(v)i i m i 1步骤(3) 计算最优值（求最短路径长度）：设有向网G含n个顶点，用邻接矩阵c[1..n, 1..n]表示，起点为s，终点为t 。
有关信息的保存：数组cost[1..n]: 存储子问题的解。
（cost[i]表示从顶点i到终点t的最短路径长度。
）数组succ[1..n]: 存储最短路径的有关信息。
（succ[i]表示顶点i到终点t的最短路径上顶点i的直接后继。
）原问题的最优值为cost[s]。
(1) 自底向上的迭代算法关键：根据递归公式确定迭代顺序（即子问题的求解顺序）。
原则：计算cost[i]时，顶点i的所有后继的cost值应先计算。
计算顺序：按图G的逆拓扑排序顺序。
算法SHORTEST_ROUTE_LEN1输入：有向网G的顶点数n, 邻接矩阵c[1..n, 1..n], 起点s和终点t , 1<=s, t<=n。
输出：G的从起点s到终点t的最短路径长度cost[s]和最短路径有关信息的数组succ[1..n]。
//对图G拓扑排序，结果存于数组a[1..n]中。
toposort(c, n, a)j=nwhile a[j]< >t j=j-1 //找出j使得a[j]=t 。
for i=j+1 to n cost[a[j]]=∞//排除无关的顶点。
cost[t]=0 //从终点开始迭代。
动态规划-最短路径问题
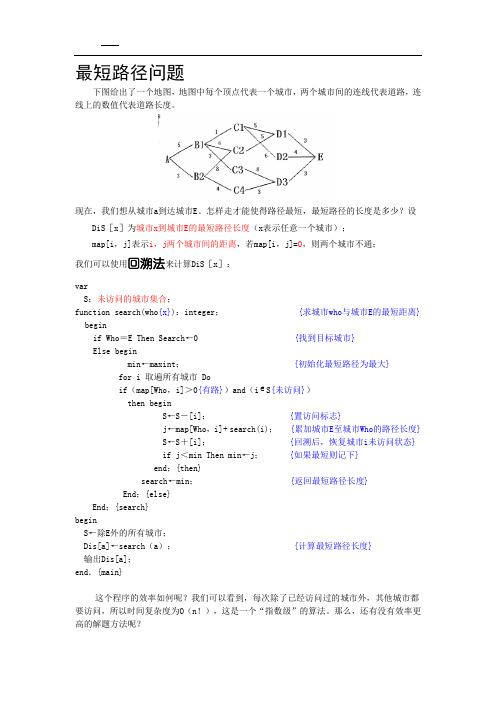
最短路径问题下图给出了一个地图，地图中每个顶点代表一个城市，两个城市间的连线代表道路，连线上的数值代表道路长度。
现在，我们想从城市a到达城市E。
怎样走才能使得路径最短，最短路径的长度是多少？设DiS［x］为城市x到城市E的最短路径长度（x表示任意一个城市）；map[i，j]表示i，j两个城市间的距离，若map[i，j]=0，则两个城市不通；我们可以使用回溯法来计算DiS［x］：varS：未访问的城市集合；function search(who{x})：integer； {求城市who与城市E的最短距离} beginif Who＝E Then Search←0 {找到目标城市}Else beginmin←maxint；{初始化最短路径为最大}for i 取遍所有城市 Doif（map[Who，i]＞0{有路}）and（i S{未访问}）then beginS←S－[i]；{置访问标志}j←map[Who，i]+ search(i)； {累加城市E至城市Who的路径长度}S←S＋[i]； {回溯后，恢复城市i未访问状态}if j＜min Then min←j； {如果最短则记下}end；{then}search←min；{返回最短路径长度}End；{else}End；{search}beginS←除E外的所有城市；Dis[a]←search（a）；{计算最短路径长度}输出Dis[a]；end．{main}这个程序的效率如何呢？我们可以看到，每次除了已经访问过的城市外，其他城市都要访问，所以时间复杂度为O（n！），这是一个“指数级”的算法。
那么，还有没有效率更高的解题方法呢？首先，我们来观察上述算法。
在求b1到E 的最短路径的时候，先求出从C2到E 的最短路径；而在求从b2刭E 的最短路径的时候，又求了一遍从C2刭E 的最短路径。
也就是说，从C2到E 的最短路径求了两遍。
同样可以发现，在求从Cl 、C2刭E 的最短路径的过程中，从Dl 到E 的最短路径也被求了两遍。
动态规划实现最短路径问题
动态规划实现最短路径问题⼀、设计最短路径的动态规划算法 <算法导论>中⼀般将设计动态规划算法归纳为下⾯⼏个步骤： 1）分析最优解的结构 2）递归定义最优解的值 3）⾃底向上计算最优解的值 4）从计算的最优解的值上⾯构建出最优解⼆、最短路径的结构 从最优解的结构开始分析(我们假设没有权值为负的路径),对于图G<V,E>的所有结点对最短路径的问题，我们能知道⼀条最短路径的⼦路径都是最短路径。
假设⽤邻接矩阵W=w(ij)来表⽰输⼊带权图,考虑从结点i到结点j的⼀条最短路径p，如果p最多有m(m为有限值)条边。
若i=j，则p的权值为0⽽且不包含其他边。
若i ≠ j，可以将i到j的路径转换为i -> k、k->j。
三、⼀个给定的图 1）给定⼀个有向图 2）我们可以给出这个有向图的邻接矩阵四、C++实现1 #include <iostream>2 #include<fstream>3 #include<sstream>4 #include<vector>5 #include<string>6using namespace std;7const int Max_Num = 100;89 typedef struct Point {10int n; //点的个数11double p[Max_Num];12double q[Max_Num];13int root[Max_Num][Max_Num];14double w[Max_Num][Max_Num];15double e[Max_Num][Max_Num];16 }Point;1718 vector<Point> points;19 vector<string> res;20 vector<int> num;2122void file_read();23void createPoint();24void optimalBST();25void printRoot(Point P);26void printOptimalBST(int i, int j, int r, Point P, ofstream &fileWrite);27 template <class Type>28 Type stringToNum(const string& str) {29 istringstream iss(str);30 Type num;31 iss >> num;32 iss.str("");33return num;34 }3536void file_read() {37string str2, str1 = "", result;38 ifstream fileRead("in.dat");39if (fileRead.is_open()) {40while (getline(fileRead, str2, '\n')) {41if (str2.find("") != -1) {42 str1.append(str2 + "");43 }44else {45 num.push_back(stringToNum<int>(str2));46if (str1 != "") {47 res.push_back(str1);48 }49 str1 = "";50 }51 }52 res.push_back(str1);53 fileRead.close();54 }55 }5657void createPoint() {58string temp;59 Point P;60for (int i = 0; i < res.size(); i++) {61 vector<string> temp_str; //存放按照空格分开后的数字62int n = num[i];63 stringstream input(res[i]);64while (input >> temp) {65 temp_str.push_back(temp);66 }67 P.n = n;68for(int k = 0; k<=n; k++) P.p[k] = stringToNum<double>(temp_str[k]);69for(int k = n + 1; k<temp_str.size(); k++) P.q[k-(n+1)] = stringToNum<double>(temp_str[k]);70 points.push_back(P);71 }72 }7374//根据书上的伪代码：接收概率列表p1....pn和q0.....qn以及规模n作为输⼊计算出e和root75void optimalBST(){76 Point P;77for(int i = 0; i<res.size(); i++) {78 vector<string> temp_str; //存放按照空格分开后的数字79int n = num[i];80string temp;81 stringstream input(res[i]);82while (input >> temp) {83 temp_str.push_back(temp);84 }85 P.n = n;8687for(int k = 0; k<=n; k++) P.p[k] = stringToNum<double>(temp_str[k]);88for(int k = n + 1; k<temp_str.size(); k++) P.q[k-(n+1)] = stringToNum<double>(temp_str[k]); 8990//初始化只包括虚拟键的⼦树91for (int i = 1;i <= P.n + 1;++i){92 P.w[i][i-1] = P.q[i-1];93 P.e[i][i-1] = P.q[i-1];94 }95//由下到上，由左到右逐步计算96for (int len = 1;len <= P.n;++len){97for (int i = 1;i <= P.n - len + 1;++i){98int j = i + len - 1;99 P.e[i][j] = Max_Num;100 P.w[i][j] = P.w[i][j-1] + P.p[j] + P.q[j];101//求取最⼩代价的⼦树的根102for (int r = i;r <= j;++r)103 {104double temp = P.e[i][r-1] + P.e[r+1][j] + P.w[i][j];105if (temp < P.e[i][j])106 {107 P.e[i][j] = temp;108 P.root[i][j] = r;109 }110 }111 }112 }113 points.push_back(P);114 }115 }116117void printOptimalBST(int i, int j, int r, Point P, ofstream &fileWrite){118int root_node = P.root[i][j];//⼦树根节点119if (root_node == P.root[1][P.n]){120//输出整棵树的根121 fileWrite << "k" << root_node << "是根" << endl;122 printOptimalBST(i, root_node - 1, root_node, P, fileWrite);123 printOptimalBST(root_node +1 , j, root_node, P, fileWrite);124return;125 }126127if (j < i - 1){128return;129 }else if (j == i - 1){//遇到虚拟键130if (j < r)131 fileWrite << "d" << j << "是" << "k" << r << "的左孩⼦" << endl;132else133 fileWrite << "d" << j << "是" << "k" << r << "的右孩⼦" << endl;134return;135 }136else{//遇到内部结点137if (root_node < r)138 fileWrite << "k" << root_node << "是" << "k" << r << "的左孩⼦" << endl; 139else140 fileWrite << "k" << root_node << "是" << "k" << r << "的右孩⼦" << endl; 141 }142 printOptimalBST(i, root_node - 1, root_node, P, fileWrite);143 printOptimalBST(root_node + 1, j, root_node, P, fileWrite);144 }145146//输出最优⼆叉查找树所有⼦树的根147void printRoot(Point P){148 cout << "各⼦树的根：" << endl;149for (int i = 1;i <= P.n;++i){150for (int j = 1;j <= P.n;++j){151 cout << P.root[i][j] << "";152 }153 cout << endl;154 }155 cout << endl;156 }157158int main(){159 file_read();160 optimalBST();161 ofstream fileWrite("out.dat");162 Point P ;163for(int i = 0; i<points.size(); i++) {164 P = points[i];165 printRoot(P);166 printOptimalBST(1,P.n,-1, P, fileWrite);167 }168 fileWrite.clear();169return0;170 } 上述代码是将给定的邻接矩阵从⽂件中读取 然后根据输⼊的邻接矩阵求出最短路径。
最短路径使用动态规划举例
动态规划最短路径举例最短路径问题。
图中给出了一个地图，地图中每个顶点代表一个城市，两个城市间的连线代表道路，连线上的数值代表道路的长度。
现在，想从城市A到达城市E，怎样走路程最短，最短路程的长度是多少?【分析】把从A到E的全过程分成四个阶段，用k表示阶段变量，第1阶段有一个初始状态A，两条可供选择的支路ABl、AB2；第2阶段有两个初始状态B1、 B2，B1有三条可供选择的支路，B2有两条可供选择的支路……。
用dk(x k，x k+1)表示在第k阶段由初始状态x k到下阶段的初始状态x k+1的路径距离，Fk(x k)表示从第k阶段的x k到终点E的最短距离，利用倒推方法求解A到E的最短距离。
具体计算过程如下：S1：K=4，有：F4(D1)=3，F4(D2)=4，F4(D3)=3S2: K=3，有：F3(C1)=min{d3(C1,D1)+F4(D1),d3(C1,D2)+F4(d2)}=min{8,10}=8F3(C2)=d3(C2,D1)+f4(D1)=5+3=8F3(C3)=d3(C3,D3)+f4(D3)=8+3=11F3(C4)=d3(C4,D3)+f4(D3)=3+3=6S2: K=2，有：F2(B1)=min{d2(B1,C1)+F3(C1),d2(B1,C2)+f3(C2),d2(B1,C3)+F3(C3)}=min {9,12,14}=9F2(m)=min{d2(B2,c2)+f3(C2),d2(B2,C4)+F3(C4)}=min{16,10}=10S4：k=1，有：F1(A)=min{d1(A,B1)+F2(B1),d1(A,B2)+F2(B2)}=min{13,13}=13因此由A点到E点的全过程的最短路径为A—>B2一>C4—>D3—>E。
最短路程长度为13。
多段图最短路径_动态规划
多段图最短路径【源程序】//本程序测试用例为作业题#include <stdio.h>//#define LOCALconstint MAX = 10000;int c[100][100];//图的存储矩阵int cost[100], path[100];intCreateGraph(){#ifdef LOCALfreopen("data.in", "r", stdin);freopen("data.out", "w", stdout);#endif // LOCALinti, j, k;int weight;//权重intvnum, arcnum;//顶点数，边数printf("请输入顶点的个数和边的个数：");scanf("%d%d",&vnum, &arcnum);for(i=0; i<vnum; i++)//初始化图的代价矩阵for(j=0; j<vnum; j++){c[i][j]=MAX;}printf("请输入边的两个顶点和权值：\n");for(k=0; k<arcnum; k++)//建立图的代价矩阵{scanf("%d%d%d",&i, &j, &weight);c[i][j]=weight;}return vnum;}intBackPath(int n)//求n个顶点的多段图的最短路径{for(inti=0; i<n-1; i++)//初始化两个数组{cost[i]=MAX;path[i]=-1;}cost[n-1]=0;//对于最后一个顶点要进行特殊的初始化path[n-1]=-1;for(inti=n-2; i>=0; i--)for(int j=i+1; j<n; j++)if(c[i][j]+cost[j]<cost[i]){cost[i]=c[i][j]+cost[j];path[i]=j;}printf("最短路径为：\n");printf("0");inti=0;while(path[i]>=0){printf("->%d",path[i]);i=path[i];}printf("\n\n");return cost[0];}int main(){int a = CreateGraph();printf("最短路径长度为：%d\n\n", BackPath(a));printf("cost数组为：\n");for(inti=0; i<a; i++)printf("%3d",cost[i]);printf("\n\n");printf("path数组为：\n");for(inti=0; i<a; i++)printf("%3d",path[i]);printf("\n");return 0;}【运行结果】。
动态规划在最短路径问题中的应用
动态规划在最短路径问题中的应用动态规划是一种解决复杂问题的方法，它将问题分解成更小的子问题，并通过保存子问题的解来避免重复计算，从而提高解决问题的效率。
最短路径问题是在图或者网络中找到从起点到终点的最短路径的问题，可以使用动态规划算法来解决。
本文将介绍动态规划在最短路径问题中的应用及其算法实现。
一、最短路径问题在最短路径问题中，我们需要在图或网络中找到从一个节点到另一个节点的最短路径。
最短路径可以通过边的权重来衡量，权重可以表示距离、时间、代价等。
最短路径问题有多种变体，其中最常见的是单源最短路径和全源最短路径。
单源最短路径问题是在给定一个起点的情况下，找到该起点到其他所有节点的最短路径。
最常用的算法是Dijkstra算法和Bellman-Ford算法。
二、动态规划原理动态规划通过保存子问题的解来避免重复计算，从而提高算法的效率。
它将问题分解成更小的子问题，并使用递推关系来计算子问题的解。
在最短路径问题中，我们可以使用动态规划来计算从起点到每个节点的最短路径。
首先，我们定义一个一维数组dist[]来保存从起点到每个节点的最短路径长度。
初始化时，dist[]的值为无穷大，表示路径长度未知。
然后，我们从起点开始逐步计算每个节点的最短路径长度。
具体的动态规划算法如下：1. 初始化dist[]为无穷大，起点的dist[]为0。
2. 对于每个节点v，按照拓扑顺序进行如下操作：2.1. 对于节点v的所有邻接节点u，如果dist[v] + weight(v, u) < dist[u]，则更新dist[u]。
2.2. 拓扑顺序可以根据节点的拓扑顺序进行计算或者使用深度优先搜索（DFS）算法。
三、算法实现下面是使用动态规划算法解决最短路径问题的示例代码：```// 定义图的邻接矩阵和节点个数int graph[MAX][MAX];int numNodes;// 定义dist[]数组来保存最短路径长度int dist[MAX];// 定义拓扑排序和DFS算法需要的变量bool visited[MAX];stack<int> s;// 动态规划算法求解最短路径void shortestPath(int startNode) {// 初始化dist[]数组为无穷大for (int i = 0; i < numNodes; i++) {dist[i] = INT_MAX;}dist[startNode] = 0;// 拓扑排序或DFS计算每个节点的最短路径长度 for (int i = 0; i < numNodes; i++) {if (!visited[i]) {DFS(i);}}// 输出最短路径长度for (int i = 0; i < numNodes; i++) {cout << "Node " << i << ": " << dist[i] << endl; }}// 深度优先搜索void DFS(int node) {visited[node] = true;for (int i = 0; i < numNodes; i++) {if (graph[node][i] != 0 && !visited[i]) {DFS(i);}}s.push(node);}```以上示例代码演示了使用动态规划算法求解最短路径问题的基本原理和步骤。
最短路径问题的动态规划算法
最短路径问题的动态规划算法动态规划是一种解决复杂问题的有效算法。
最短路径问题是指在给定的图中找到从起点到终点路径中距离最短的路径。
本文将介绍动态规划算法在解决最短路径问题中的应用。
1. 最短路径问题简介最短路径问题是图论中的经典问题之一，旨在找到从图中一点到另一点的最短路径。
通常使用距离或权重来衡量路径的长度。
最短路径问题有多种算法可以解决，其中动态规划算法是一种常用且高效的方法。
2. 动态规划算法原理动态规划算法的核心思想是将原问题分解为更小的子问题，并存储已解决子问题的结果，以供后续使用。
通过逐步解决子问题，最终得到原问题的解。
在最短路径问题中，动态规划算法将路径分解为多个子路径，并计算每个子路径的最短距离。
3. 动态规划算法步骤（1）定义状态：将问题转化为一个状态集合，每个状态表示一个子问题。
（2）确定状态转移方程：通过递推或计算得到子问题之间的关系，得到状态转移方程。
（3）确定初始状态：设置与最小子问题相关的初始状态。
（4）递推求解：根据状态转移方程，逐步计算中间状态，直到得到最终解。
（5）回溯路径：根据存储的中间状态，找到最短路径。
4. 动态规划算法示例以经典的Dijkstra算法为例，演示动态规划算法在解决最短路径问题中的应用。
假设有带权重的有向图G，其中节点数为n，边数为m。
算法步骤如下：（1）定义状态：对于图G中的每个节点v，定义状态d[v]代表从起点到节点v的最短距离。
（2）确定状态转移方程：d[v] = min(d[u]+w[u,v])，其中u为节点v 的直接前驱节点，w[u,v]为边(u,v)的权重。
（3）确定初始状态：设置起点s的最短距离d[s]为0，其他节点的最短距离d[v]为无穷大。
（4）递推求解：根据状态转移方程逐步计算中间状态d[v]，更新最短距离。
（5）回溯路径：根据存储的前驱节点，从终点t开始回溯，得到最短路径。
5. 动态规划算法的优缺点优点：（1）求解速度快，适用于大规模问题。
经典算法之多段图算法
每个点之间有无路径采用一个二维数组表示，即 mix[i][j]为从节点 i 到节点 j 的路径， 如பைடு நூலகம்不存在则 mix[i][j]=0； #include <iostream> using namespace std; void out(int mix[11][11]) {
};
out(mix); return 0; }
输出
最后一个值 14 即从首节点到目标节点的最短距离。 更多编程算法内容请登录 IT 部落格()
//思想是把每个节点假如进来，并且每加入一个节点，则更新值 int i=1; int len[11]={0}; while(i<11) {
//先找到该节点的所有前驱 int total=100000; for(int j=0;j<i;j++) {
if(mix[j][i]!=0) {
//判断是否存在到该节点的路径，如果有则根据路径长度更新 if(total>(mix[j][i]+len[j])) {
第一步，计算从第一层到首节点的距离，因为是第一层，因此不需要最小值函数，直 接记录首节点的距离即可。
第二步，展开第三层的节点，每个节点计算从前一层的可达路径，并且用 min 函数查 出最小值，并且记录最小值和取得最小值的前驱点。
重复上述过程。
重复上述过程。
在完成上述过程后，逆向查找前驱节点即可找到最短路径。
动态规划思想采用动态规划法从初始点开始每次更新最新的一段的节点距离得到最短距离重复该该过程直至达到目标节点
经典算法之多段图算法 1、 算法概述
如图，计算出节点 1 到节点 11 的最短路径，其中箭头中的数字代表从该节点到下一个 节点的距离。
算法设计与分析-多段图最短路径问题
关于多段图最短路径问题的探讨摘要：本文主要描述的是分别用动态规划法、贪心法和分支限界法来解决多段图最短路径问题时的情况，并在附录中附有实际问题的程序来辅助阐述观点。
文章首先阐述了各个方法的原理，主要的思路是通过输入一组数据，比较三者的输出结果的准确性以及运行时间，以之为基础来分析、讨论三者的性能区别。
另外，众所周知，多段图是有向图的一个简单的模型，它在有向图的基础上忽略了两点之间的线的双向性的问题，并且对点与点之间的线有很多的要求，从而把图简化为可分为几段的模式，文章最后讲述了若这几种方法运行到有向图中的情况，几种方法的对比和它们比较适应的使用情况的讨论，并给出了自己的建议。
关键字：多段图最短路径问题动态规划法分支限界法多段图与有向图的关系有向图最短路径算法引言：当前社会，关于最短路径的问题屡屡出现。
例如在开车自驾游的一个过程中，排除其他影响因素，从一个地点到另一点，这个时候必然是希望有一条距离最短的路程来尽量减少消耗的时间以及花费的（它们在模型中被称为代价），市场上对该问题的解决有很大的需求，因此，这里我将讨论多段图的最短路径的问题。
在早些时间的课程中，我们学习过数据结构这门课程，其中就包括最短路径这方面的讨论。
当时老师给我们介绍了分别面向单源（Dijkstra算法）与非单源（Floyd算法）两种问题的算法法---，这是我们最早的对最短路径方面的理解，也是我们接触的比较早的关于图的问题。
在这学期的算法课程中，我们学习了许多了方法，包括贪心法、动态规划法等算法，它们把以前学习的许多方法都命名并归纳分类起来，其中有许多算法都是可以用来解决这个最短路径的问题的，并且该问题作为一个图的问题，对该问题的继续探讨优化的需求很大，本文将就不同算法在解决该最短路径问题时的不同方法进行对比并给出该问题在不同基础上不同的最终解决方案。
由于时间的限制，本文将重点分析动态规划法下的情况，并会对图的情况加以简化、限制，最后会对其他的图做一些拓展。
动态规划之最短路径源代码
动态规划之最短路径问题源代码#include "stdio.h"#include "conio.h"#define n 16 /*图的顶点数*/#define k 7 /*图的段数*/#define l 30#define MAX 100typedef int NodeNumber;/*节点编号*/typedef int CostType;/*成本值类型*/CostType cost[n][n];NodeNumber path[k];NodeNumber cur=-1;void creategraph(CostType *cost[n][n]) /*创建图的成本矩阵*/ {int i,j,x,y,value;for(i=0;i<n;i++)for(j=0;j<n;j++) cost[i][j]=0;printf("\nEnter the cost of graph:\n");for(i=0;i<l;i++){scanf("%d,%d,%d",&x,&y,&value);cost[x][y]=value;}}void outgraph(CostType *cost[n][n]) /*输出图的成本矩阵*/ {int i,j;printf("Print the cost of graph:\n");for(i=0;i<n;i++){for(j=0;j<n;j++) printf("%2d",cost[i][j]);printf("\n");}}/*使用向前递推算法求多段图的最短路径*/void FPath(CostType *cost[n][n],NodeNumber *path[k]) {int i,j,leng,temp,v[n],d[n];for(i=0;i<n;i++) v[i]=0;for(i=n-2;i>=0;i--){ leng=MAX;for(j=i+1;j<=n-1;j++)if(cost[i][j]>0 && (cost[i][j]+v[j])<leng){leng=cost[i][j]+v[j];temp=j;}v[i]=leng;d[i]=temp;}path[0]=0;path[k-1]=n-1;for(i=1;i<=k-2;i++) path[i]=d[path[i-1]]; }/*输出最短路径序列*/void outpath(NodeNumber *path[k]){int i;printf("\nPrint the shortest treet:\n");for(i=0;i<k;i++) printf("%3d",path[i]); }main(){NodeNumber m,t;creategraph(&cost);outgraph(&cost);FPath(&cost,&path);outpath(&path);}。
动态规划算法实现多段图的最短路径问题算法设计与分析实验报告
动态规划算法实现多段图的最短路径问题算法设计与分析实验报告算法设计与分析实验报告实验名称 动态规划算法实现多段图的最短路径问题 评分 实验日期 年 月 日 指导教师 姓名 专业班级 学号一.实验要求1. 理解最优子结构的问题。
有一类问题的活动过程可以分成若干个阶段，而且在任一阶段后的行为依赖于该阶段的状态，与该阶段之前的过程如何达到这种状态的方式无关。
这类问题的解决是多阶段的决策过程。
在50年代，贝尔曼（Richard Bellman ）等人提出了解决这类问题的“最优化原理”，从而创建了最优化问题的一种新的算法设计方法－动态规划。
对于一个多阶段过程问题，是否可以分段实现最优决策，依赖于该问题是否有最优子结构性质，能否采用动态规划的方法，还要看该问题的子问题是否具有重叠性质。
最优子结构性质：原问题的最优解包含了其子问题的最优解。
子问题重叠性质：每次产生的子问题并不总是新问题，有些子问题被反复计算多次。
问题的最优子结构性质和子问题重叠性质是采用动态规划算法的两个基本要素。
2.理解分段决策Bellman 方程。
每一点最优都是上一点最优加上这段长度。
即当前最优只与上一步有关。
U s 初始值，u j 第j 段的最优值。
⎪⎩⎪⎨⎧+==≠}.{min ,0ijiji js w u u u3.一般方法1）找出最优解的性质，并刻画其结构特征；2）递归地定义最优值（写出动态规划方程）；3）以自底向上的方式计算出最优值；4）根据计算最优值时得到的信息，构造一个最优解。
步骤1-3是动态规划算法的基本步骤。
在只需要求出最优值的情形，步骤4可以省略，步骤3中记录的信息也较少；若需要求出问题的一个最优解，则必须执行步骤4，步骤3中记录的信息必须足够多以便构造最优解。
二.实验内容1.编程实现多段图的最短路径问题的动态规划算法。
2.图的数据结构采用邻接表。
3.要求用文件装入5个多段图数据，编写从文件到邻接表的函数。
4.验证算法的时间复杂性。
基于动态规划的最短路径算法设计与优化
基于动态规划的最短路径算法设计与优化一、绪论最短路径问题是一个经典的计算机科学问题，在众多领域中都有着广泛的应用，如网络路由、物流配送、地图导航等。
本文将讨论如何运用动态规划方法来求解最短路径问题，并从算法设计和算法优化两个方面入手，提高算法的效率和性能。
二、最短路径问题的动态规划解法1. 最短路径的定义在一张有向带权图中，从起点s到终点t的一条路径，如果它的边权之和最小，那么我们称这条路径是最短路径。
2. 最短路径问题的动态规划解法基本原理我们可以将最短路径问题转化为子问题，定义d[v]表示从起点s到顶点v的最短距离，那么d[t]就是问题的解。
记G=(V,E)为一张有向带权图，我们要求的就是d[t]。
在进行最短路径的动态规划时，我们主要运用的是最优子结构和重复计算问题。
最优子结构的原理如下：一条最短路径可以被拆分为多个“次优解”，每个“次优解”都可以用更小的“次优解”组合而成，直到组合到最短路径为止。
重复计算问题的原理如下：在计算d[v]时，需要先计算出所有以v为终点的边的起点u的最短路径，这些最短路径构成了一个集合P。
如果直接使用暴力算法，则有可能会重复计算P中的某些路径。
运用动态规划，我们可以将已经计算出的最短路径结果保存起来，每次需要计算时可以直接调用，避免了重复计算的问题。
3. 最短路径问题的动态规划解法步骤定义数组d[V]，其中d[s]=0，d[v]=+ɛ(v≠s)。
按拓扑排序的顺序遍历有向带权图，对于每个顶点v，更新所有以v为终点的边的起点u的最短路径，即：d[v]=min(d[u]+w[u,v])，其中w[u,v]表示边(u,v)的权值。
4. 最短路径问题的动态规划算法实现算法实现的代码如下：void dp_shortest_path(Graph *G, int s, int *d) {int t, i, v, u, p;for (i = 0; i < G->vexnum; ++i) d[i] = INF;d[s] = 0;for (t = 1; t < G->vexnum; ++t) {for (v = 0; v < G->vexnum; ++v) {for (p = G->v[v].first; p != -1; p = G->arc[p].next) {u = G->arc[p].adjvex;if (d[u] + G->arc[p].weight < d[v]) {d[v] = d[u] + G->arc[p].weight;}}}}}三、最短路径算法的优化1. Dijkstra算法优化Dijkstra算法是一种贪心算法，它适用于有权图的最短路径问题，算法的基本思路是：每次找到离起点最近的尚未确定最短路径的顶点v，更新v的所有邻接点的距离，直到找到终点或路径无法更新为止。
最短路径问题的动态规划算法
最短路径问题的动态规划算法最短路径问题的动态规划算法是一种常用的解决路径优化的方法。
动态规划算法的核心思想是将原问题拆分成若干个子问题，通过递推关系找到最优解。
在最短路径问题中，我们通常希望找到从起点到终点的最短路径。
首先，我们需要定义一个二维数组dp，其中dp[i][j]表示从起点到达坐标(i, j)的最短路径长度。
初始化dp数组，将起点的值设为0，其他位置的值设为无穷大（即表示不可达）。
接下来，我们需要确定动态规划的状态转移方程。
对于任意一个坐标(i, j)，它可以从上方的坐标(i-1, j)、左方的坐标(i, j-1)、右方的坐标(i, j+1)、下方的坐标(i+1, j)四个位置中的某一个到达。
因此，可以得到状态转移方程如下：
dp[i][j] = min(dp[i-1][j], dp[i][j-1], dp[i][j+1], dp[i+1][j]) + 1
其中，min表示取其中的最小值。
通过以上状态转移方程，我们可以逐步更新dp数组，直到最终得到终点的最短路径长度。
需要注意的是，动态规划算法的时间复杂度通常是O(n^2)，其中n 表示问题规模。
因此，在处理大规模最短路径问题时，需要考虑算法的效率，可能需要进行剪枝等优化操作。
总的来说，最短路径问题的动态规划算法在路径优化领域有着重要的应用价值，通过合理定义状态转移方程和优化算法效率，可以找到从起点到终点的最短路径长度，为路径规划提供有效的解决方案。
浅谈最短线路及其动态规划
浅谈最短线路及其动态规划最短路问题是一个组合优化问题，它不但可以被直接用于解决生产生活中的很多实际问题，而且常常被作为一种有效工具，用于解决其他优化问题.本文将最短路问题及其动态规划谈一些自己粗浅的认识。
标签：最短路；描述；动态规划最短路问题是最基本的组合优化问题之一，随着我国经济水平的迅猛发展和城市化过程的加快，城市交通线路已进入飞速发展时期，最短路算法在人们的日常生活中显得越来越重要.比如，每天开车去上班，应该选择哪条路线才能使自己到单位的费用最低、时间最少，这是最短路的问题；在电网架设、城市规划以及交通旅游中如何使其耗费的资金最少，这也是最短路问题；管道设计问题，给出一个网络图，从A点铺设一条煤气管道到E点，必须经过三个中间站，如何选择路线使得铺设的管道费用最少，这还是最短路问题.目前，最短路问题及其算法在实际生活的各个领域中应用广泛.计算机C语言，运筹学以及图论中的某些重要思想都在涉及最短路问题及其算法问题，并且被普遍应用于农业，军事以及重型工业和交通等等.由此可见研究最短路问题是非常有意义的.很多参考文献对最短路问题及其算法进行了讨论，文献[1-3]讨论了最短初等链法，给出了最短初等链法是最短路问题的通用算法的结果，文献[4-6]介绍了最短路问题的动态规划算法，给出了算法的基本思想与解题步骤，文献[7-9]介绍了伏特算法，给出了算法的具体步骤与适用的问题类型，文献[10-11]介绍了最短路问题的狄克斯特拉算法，通过对算法基本步骤的了解，为提高其搜索速度提出了一种新的算法，文献[12-13]介绍了狄克斯特拉算法的局限性，给出此算法不适于具有负弧长的情形.一、最短路程问题描述在图论中关于最短路问题的提法是：设图G=（V，E）为连通图，对G的每一条边，相应的有一个数（简记作）称为边的权（表示到无关联边），图G连同在它边上的权称为赋权图.设H是赋权图G的子图，H的权是它的每一条边的权的和.在赋权图中，一条边的权也可说成是它的长.若在赋权图中任取两点和，所谓最短道路就是求出一条路μ，它表示的是从到的全部路中总权最小的路[2]，即最短路问题在图论中的应用比较广泛，它包含许多生活中的实际问题，如各种管道的铺设、线路的安排、输送网络最少费用等问题，通过建立最短路问题模型都可以进行求解.二、最短路程問题的动态规划动态规划处理的问题是一个多阶段的决策问题，一般从初始状态开始，经过对中间阶段的决策选择，最终达到结束状态.这些决策形成一个决策序列，同时也确定了一条整个过程的活动路线.动态规划的设计有一定的模式，通常要经历以下几个步骤：初始状态→│决策1│→│决策2│→…→│决策n│→结束状态.利用动态规划解题的基本思路：将一个多阶段的决策问题转化成依次求解多个单阶段的决策问题，进而简化计算的过程，这种方法的实现就是从终点反向递推，即采用逆序算法.若赋权图1以A为起点，以D为终点，如何求出以A为起点，以D为终点的最短路？应用动态规划算法求解上述问题的基本思想是：（1）把以A为起点的全部链的终点按链的长度进行分类.如图1所示，以A 为起点的全部链的终点根据链的长度被分为4部分，可用集合分别表为：每一部分称为一个状态，相邻的两个状态以及由它们间的有向线段构成的有向边记做一个阶段，任一条边都含有一个权值，图1是赋权三阶段有向图.图1 赋权三阶段有向图（2）利用逆序递推的方法进行求解，从最后一阶段一直到第一阶段分别逐步求出每点到终点的最短路，最后再求起点A到终点D的最短路.利用动态规划描述多阶段决策问题的基本概念[7]有：阶段与阶段变量k，决策与决策变量，策略与最优策略，指标函数与最优指标函数，状态与状态变量，状态的转移方程，阶段指标（阶段效益）等.从第k阶段状态起至第n阶段终止状态过程中的策略，指标函数及最优值函数可分别用式（1）～式（4）表示.（1）（2）（3）（4）动态规划的基本方程：在动态规划中有2种算法：顺序递推和逆序递推.顺序递推就是从始点向终点逐段的递推，而逆序递推则是从终点向始点逐段的递推[3].若一个多阶段的决策问题有一个固定的过程始点和一个固定的过程终点，那么2种递推方法所得到的最优结果是相同的.参考文献[1]刘道建.最短路问题的通用算法--最短初等链法[J].湘潭师范学院学报，2003，25（2）：11-13.[2]郭锐.最优化算法中的最短路问题讨论[J].大庆师范学院学报，2008，28（2）：75-78.。
多段图的最短路劲问题,动态规划法 分析最优性原理
多段图的最短路劲问题,动态规划法分析最优性原理我们都知道，无论是初中还是高中，数理化的学习过程中都是非常重要的。
其中，最短路劲问题，是数学考试当中常考的题型之一。
它的难度在初中数学中是比较大的。
很多同学在学习该题的时候也十分头疼，因为该问题通常采用动态规划法求解即可。
所谓动态规划法，其实就是由求解方程组而得到结论最优的方法。
那么今天我们就来学习一下如何进行简单易操作并将其运用于实际之中吧！一、解题思路通过观察题目，我们可以得到题目中由图 a,图 b组成的最短路劲问题的求解法：求 a={a, b, c},其中 a、 b、 c表示两段图之间的相交点。
求 a最短路劲，我们可以根据不同的情况选择不同的方法来求解。
当我们在做题过程中遇到困难时，可以通过求解最短路劲问题来了解分析它所需要处理的基本数学原理，从而达到解决此题的目的。
根据题目中提供的信息可知，多段图对于图 b而言，最短路劲要求它具有不同的解题思路。
二、求最优解的基本方法最优解的求解方法有两种：一者为连续变量的最大值问题，二者为连续不变量。
这种问题的解决方法一般为：以图中 A点的起始位置（也就是 A与 B)作为计算基点，依次以 A点、 B 点进行一次求解方程组，再将方程组进行解析，得到最优解；或者以相同的方法求出各点的余数，得出最优解。
求解过程中需要注意两个问题：第一个问题是求方程组时不一定要选择整数、整列代入、整阶运算；第二个问题只要找到方程中关键的最优解即可。
所以在求最优解时需要掌握正确的方法，同时也要注意以下几个方面：三、动态规划法分析分析：将图中已知状态矩阵代入所求题中，可得到：设图中状态矩阵 B和状态矩阵 A是多段图中唯一正确状态的解，因此 B和 C是正确的解；设状态矩阵 A是已知状态矩阵-状态式解，则 AC和 AC是正确的解；由于状态矩阵 B和状态矩阵 A是正确方程组式外部分与状态矩阵 a、b、 c、 d四等分函数相关，因此 AC和 AC就是正确方程组。
动态规划在最短路径问题中的应用
动态规划在最短路径问题中的应用最短路径问题是计算两个给定节点之间的最短路径的问题。
在现实生活和计算机科学中，这个问题经常出现。
一种常用的解决方法是动态规划。
本文将介绍动态规划在最短路径问题中的应用。
动态规划是一种用于解决优化问题的算法思想。
它通常用于寻找最优解，避免重复计算。
在最短路径问题中，动态规划可以帮助我们找到从起点到终点的最短路径。
为了更好地理解动态规划在最短路径问题中的应用，我们先来介绍一下最短路径问题的定义。
最短路径问题可以建模成一个图的问题，其中节点表示位置，边表示路径。
每条边都有一个相关的权重，表示从一个节点到另一个节点的代价或距离。
目标是找到从起点到终点的最短路径。
现在，我们来看一下动态规划如何解决最短路径问题。
首先，我们定义一个二维数组dp，其中dp[i][j]表示从起点到节点i的最短路径的权重。
我们将所有的dp[i][j]初始值设为无穷大，表示路径不存在。
接下来，我们需要定义一些转移方程来更新dp数组的值。
对于节点i和节点j之间存在一条边的情况，我们可以使用如下的转移方程来更新dp[i][j]：dp[i][j] = min(dp[i][j], dp[i][k]+dp[k][j]+w[i][j])其中，k是一个介于i和j之间的节点，w[i][j]是从节点i到节点j的边的权重。
这个转移方程表示，如果从起点到节点k的路径加上从节点k到终点的路径再加上边的权重，比当前的dp[i][j]的值小，那么我们更新dp[i][j]的值。
通过不断更新dp数组的值，我们最终可以得到从起点到终点的最短路径的权重。
同时，我们还可以通过修改转移方程来记录路径上的节点，从而得到最短路径。
在实际应用中，动态规划在最短路径问题中有着广泛的应用。
例如，在导航系统中，我们可以使用动态规划算法来计算从当前位置到目的地的最短路径。
在网络路由中，动态规划可以帮助我们找到从源节点到目标节点的最短路径。
总结一下，动态规划是一种解决优化问题的算法思想，在最短路径问题中有着重要的应用。
算法分析期末考试集答案（套）
算法分析期末考试集答案（套）《算法分析与设计》⼀、解答题 1. 机器调度问题。
问题描述：现在有n 件任务和⽆限多台的机器，任务可以在机器上得到处理。
每件任务的开始时间为s i ，完成时间为f i ，s i问题实例：若任务占⽤的时间范围是{[1，4]，[2，5]，[4，5]，[2，6]，[4，7]}，则按时完成所有任务最少需要⼏台机器？（提⽰：使⽤贪⼼算法）画出⼯作在对应的机器上的分配情况。
2. 已知⾮齐次递归⽅程：f (n)bf (n 1)g(n)f (0)c =-+??=? ，其中，b 、c 是常数，g(n)是n 的某⼀个函数。
则f(n)的⾮递归表达式为：nnn i i 1f (n)cb b g(i)-==+∑。
现有Hanoi 塔问题的递归⽅程为：h(n)2h(n 1)1h(1)1=-+??=? ，求h(n)的⾮递归表达式。
解：利⽤给出的关系式，此时有：b=2, c=1, g(n)=1, 从n 递推到1，有：n 1n 1n 1i i 1n 1n 22n h(n)cbb g(i)22 (22121)----=--=+=+++++=-∑3. 单源最短路径的求解。
问题的描述：给定带权有向图（如下图所⽰）G =(V,E)，其中每条边的权是⾮负实数。
另外，还给定V 中的⼀个顶点，称为源。
现在要计算从源到所有其它各顶点的最短路长度。
这⾥路的长度是指路上各边权之和。
这个问题通常称为单源最短路径问题。
解法：现采⽤Dijkstra 算法计算从源顶点1到其它顶点间最短路径。
请将此过程填⼊下表中。
4. 请写出⽤回溯法解装载问题的函数。
装载问题：有⼀批共n 个集装箱要装上2艘载重量分别为c1和c2的轮船，其中集装箱i 的重量为wi ，且121nii w c c=≤+∑。
装载问题要求确定是否有⼀个合理的装载⽅案可将这n 个集装箱装上这2艘轮船。
如果有，找出⼀种装载⽅案。
解：void backtrack (int i){// 搜索第i 层结点if (i > n) // 到达叶结点更新最优解bestx,bestw;return; r -= w[i];if (cw + w[i] <= c) {// 搜索左⼦树43 2 1 100 30 maxint10 - {1} 初始 dist[5] dist[4] dist[3] dist[2] u S 迭代x[i] = 1;cw += w[i];backtrack(i + 1);cw -= w[i]; }if (cw + r > bestw) {x[i] = 0; // 搜索右⼦树backtrack(i + 1); }r += w[i];}5. ⽤分⽀限界法解装载问题时，对算法进⾏了⼀些改进，下⾯的程序段给出了改进部分；试说明斜线部分完成什么功能，以及这样做的原因，即采⽤这样的⽅式，算法在执⾏上有什么不同。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
多段图最短路径【源程序】
//本程序测试用例为作业题
#include <stdio.h>
//#define LOCAL
constint MAX = 10000;
int c[100][100];//图的存储矩阵
int cost[100], path[100];
intCreateGraph()
{
#ifdef LOCAL
freopen("data.in", "r", stdin);
freopen("data.out", "w", stdout);
#endif // LOCAL
inti, j, k;
int weight;//权重
intvnum, arcnum;//顶点数，边数
printf("请输入顶点的个数和边的个数：");
scanf("%d%d",&vnum, &arcnum);
for(i=0; i<vnum; i++)//初始化图的代价矩阵
for(j=0; j<vnum; j++)
{
c[i][j]=MAX;
}
printf("请输入边的两个顶点和权值：\n");
for(k=0; k<arcnum; k++)//建立图的代价矩阵
{
scanf("%d%d%d",&i, &j, &weight);
c[i][j]=weight;
}
return vnum;
}
intBackPath(int n)//求n个顶点的多段图的最短路径
{
for(inti=0; i<n-1; i++)//初始化两个数组
{
cost[i]=MAX;
path[i]=-1;
}
cost[n-1]=0;//对于最后一个顶点要进行特殊的初始化path[n-1]=-1;
for(inti=n-2; i>=0; i--)
for(int j=i+1; j<n; j++)
if(c[i][j]+cost[j]<cost[i])
{
cost[i]=c[i][j]+cost[j];
path[i]=j;
}
printf("最短路径为：\n");
printf("0");
inti=0;
while(path[i]>=0)
{
printf("->%d",path[i]);
i=path[i];
}
printf("\n\n");
return cost[0];
}
int main()
{
int a = CreateGraph();
printf("最短路径长度为：%d\n\n", BackPath(a));
printf("cost数组为：\n");
for(inti=0; i<a; i++)
printf("%3d",cost[i]);
printf("\n\n");
printf("path数组为：\n");
for(inti=0; i<a; i++)
printf("%3d",path[i]);
printf("\n");
return 0;
}
【运行结果】。