数值分析2012考试卷沈阳工业大学

合集下载

数值分析试题与答案

一、单项选择题（每小题3分,共15分）1. 和分别作为π(de)近似数具有（）和（）位有效数字. A ．4和3 B ．3和2 C ．3和4 D ．4和42. 已知求积公式()()211211()(2)636f x dx f Af f ≈++⎰,则A ＝（）A ． 16B ．13C ．12D ．233. 通过点()()0011,,,x y x y (de)拉格朗日插值基函数()()01,l x l x 满足（）A ．()00l x ＝0,()110l x =B ．()00l x ＝0,()111l x =C ．()00l x ＝1,()111l x = D ．()00l x ＝1,()111l x =4. 设求方程()0f x =(de)根(de)牛顿法收敛,则它具有（）敛速.A ．超线性B ．平方C ．线性D ．三次5. 用列主元消元法解线性方程组1231231220223332x x x x x x x x ++=⎧⎪++=⎨⎪--=⎩ 作第一次消元后得到(de)第3个方程（）.A ．232x x -+=B ．232 1.5 3.5x x -+=C ．2323x x -+=D ．230.5 1.5x x -=-二、填空题（每小题3分,共15分）1. 设TX )4,3,2(-=, 则=1||||X ,2||||X = .2. 一阶均差()01,f x x =3. 已知3n =时,科茨系数()()()33301213,88C C C ===,那么()33C = 4. 因为方程()420x f x x =-+=在区间[]1,2上满足 ,所以()0f x =在区间内有根.5. 取步长0.1h =,用欧拉法解初值问题()211y y yx y ⎧'=+⎪⎨⎪=⎩(de)计算公式 .0,1,2分人三、计算题（每题15分,共60分）1. 已知函数211y x =+(de)一组数据：求分段线性插值函数,并计算()1.5f (de)近似值.1. 解 []0,1x ∈,()1010.510.50110x x L x x --=⨯+⨯=---[]1,2x ∈,()210.50.20.30.81221x x L x x --=⨯+⨯=-+--所以分段线性插值函数为()[][]10.50,10.80.31,2x x L x x x ⎧-∈⎪=⎨-∈⎪⎩ ()1.50.80.3 1.50.35L =-⨯=2. 已知线性方程组1231231231027.21028.35 4.2x x x x x x x x x --=⎧⎪-+-=⎨⎪--+=⎩（1）写出雅可比迭代公式、高斯－塞德尔迭代公式；（2）对于初始值()()00,0,0X =,应用雅可比迭代公式、高斯－塞德尔迭代公式分别计算()1X （保留小数点后五位数字）.1.解原方程组同解变形为1232133120.10.20.720.10.20.830.20.20.84x x x x x x x x x =++⎧⎪=-+⎨⎪=++⎩雅可比迭代公式为()()()()()()()()()1123121313120.10.20.720.10.20.830.20.20.84m m m m m m m m m x x x x x x x x x +++⎧=++⎪⎪=-+⎨⎪=++⎪⎩(0,1...)m =高斯－塞德尔迭代法公式()()()()()()()()()1123112131113120.10.20.720.10.20.830.20.20.84m m m m m m m m m x x x x x x x x x ++++++⎧=++⎪⎪=-+⎨⎪=++⎪⎩ (0,1...)m =用雅可比迭代公式得()()10.72000,0.83000,0.84000X =用高斯－塞德尔迭代公式得()()10.72000,0.90200,1.16440X =3. 用牛顿法求方程3310x x --=在[]1,2之间(de)近似根（1）请指出为什么初值应取2 （2）请用牛顿法求出近似根,精确到. 3. 解()331f x x x =--,()130f =-<,()210f =>()233f x x '=-,()12f x x ''=,()2240f =>,故取2x =作初始值4. 写出梯形公式和辛卜生公式,并用来分别计算积分111dxx+⎰.四、证明题（本题10分）确定下列求积公式中(de)待定系数,并证明确定后(de)求积公式具有3次代数精确度()()()()1010hhf x dx A f h A f A f h --=-++⎰证明：求积公式中含有三个待定系数,即101,,A A A -,将()21,,f x x x =分别代入求一、填空（共20分,每题2分）1. 设2.3149541...x *=,取5位有效数字,则所得(de)近似值x= .2.设一阶差商()()()21122114,321f x f x f x x x x --===---,()()()322332615,422f x f x f x x x x --===--则二阶差商 ()123,,______f x x x =3. 设(2,3,1)TX =--, 则2||||X = ,=∞||||X .4．求方程 21.250x x --= (de)近似根,用迭代公式 1.25x x =+,取初始值 01x =, 那么 1______x =。

2012数值分析试题及答案

aii
(bi

n
aij
x
(k j
)
)
,
j 1
i 1,2,, n
(1) 求此迭代法的迭代矩阵 M ；
(2) 证明：当 A 是严格对角占优矩阵， 0.5 时，此迭代格式收敛.
解：迭代法的矩阵形式为：
x(k1) x(k) D 1 (b Ax (k) ) D 1 (D A)x(k) D 1b
x2 3/5
）.
线 …
8．对离散数据 xi yi
1 0 1 2 的拟合曲线 y 5 x 2 的均方差为( 2.5 1.58 ).
2 1 1 3
6
…
…
…
9．设求积公式
2
f (x)dx
1
A0 f (1) A1 f (0) A2 f (1) 是插值型求积公式，则积分系
… 数 A0 3/ 4 , A1 0 , A2 9 / 4 .
2
2
2
2
2
2
R[ f ] 0 f (x)dx 0 p1 (x)dx 0 f (x)dx 0 H 3 (x)dx 0 H 3 (x)dx 0 p1(x)dx
2 f (4) ( x ) (x 1 )2 (x 1 )2 dx f (4) () 2 (x2 1)2 dx
…
四、(10 分)利用复化 Simpson 公式 S2 计算定积分 I
2
cos
xdx
的近似值，并估
0
… 计误差。
… …
解：
I

S2

1 [cos0 6
cos2

数值分析期末考试和答案

数值分析期末考试和答案一、单项选择题（每题2分，共20分）1. 在数值分析中，下列哪个方法用于求解线性方程组？A. 插值法B. 迭代法C. 直接法D. 拟合法答案：C2. 以下哪个数值方法是用于求解非线性方程的？A. 高斯消元法B. 牛顿迭代法C. 线性插值法D. 拉格朗日插值法答案：B3. 在数值积分中，梯形法则的误差与下列哪个因素无关？A. 被积函数的二阶导数B. 积分区间的长度C. 积分区间的划分数量D. 被积函数的一阶导数答案：D4. 以下哪个数值方法是用于求解常微分方程的？A. 欧拉方法B. 牛顿迭代法C. 拉格朗日插值法D. 高斯消元法答案：A5. 在数值分析中，下列哪个方法用于求解特征值问题？A. 高斯消元法B. 幂迭代法C. 牛顿迭代法D. 梯形法则答案：B6. 以下哪个数值方法是用于求解线性最小二乘问题的？A. 高斯消元法B. 梯形法则C. 正交分解法D. 牛顿迭代法答案：C7. 在数值分析中，下列哪个方法用于求解非线性方程组？A. 高斯消元法B. 牛顿迭代法C. 线性插值法D. 欧拉方法答案：B8. 在数值分析中，下列哪个方法用于求解偏微分方程？A. 有限差分法B. 牛顿迭代法C. 线性插值法D. 梯形法则答案：A9. 在数值分析中，下列哪个方法用于求解优化问题？A. 高斯消元法B. 梯形法则C. 牛顿迭代法D. 单纯形法答案：D10. 在数值分析中，下列哪个方法用于求解插值问题？A. 高斯消元法B. 梯形法则C. 牛顿迭代法D. 拉格朗日插值法答案：D二、填空题（每题2分，共20分）1. 在数值分析中，求解线性方程组的直接法包括______消元法和______消元法。

答案：高斯；LU2. 牛顿迭代法的收敛速度是______阶的。

答案：二3. 梯形法则的误差与被积函数的______阶导数有关。

答案：二4. 欧拉方法是一种求解______阶常微分方程的数值方法。

答案：一5. 幂迭代法是求解______特征值问题的数值方法。

2012研究生试题数值分析数值分析

第 5页共 6 页
七、（本题满分 10 分）试推导下列求积公式
∫b f (x)dx ≈ (b − a) f ( a + b)
a
2
的截断误差的表达式，并判断其代数精度。
第 6页共 6 页
2 3 3、设 A = 1 1 ，则 Cond∞ ( A) = ______. 4、已知 3 阶矩阵 A 的特征值分别为 2,-5,6，则矩阵 A 的谱半径是___________. 5、已知 f (x) = x − sin x −1 ，则牛顿法的迭代公式是_______________
第 2页共 6 页
四、（本题满分 10 分）求函数 f (x) = sin π x 在区间 [0 ， 1] 上的最佳平方逼近多项式 ϕ(x) = a + bx2 。
第 3）试用数值积分法建立常微分方程初值问题：
dy dx
x3 +
=1 x3 =
3
取初始向量 x(0) = [0,0,0]T 迭代求解，求到 x(2) 。
第 1页共 6 页
三、（本题满分 10 分）已知数据表:
x -1 0 1 2 3 y2 1 3 4 5
通过构造点集 {−1, 0,1, 2,3} 上的正交多项式求一个二次多项式以最小二乘法拟
合上述数据。
10、将向量 s = (−2,1, 0)T 变为与 e1 = (1, 0, 0)T 同向的变换 u = Hs 中的 Householder 矩阵
H = ______。
二、（本题满分 10 分）用 Gauss-Seidel 迭代法求解方程组

x1
+
2x2
−
2x3

2012年春季学期(本科生)数值分析课程考试试卷(A卷)答案及评分标准

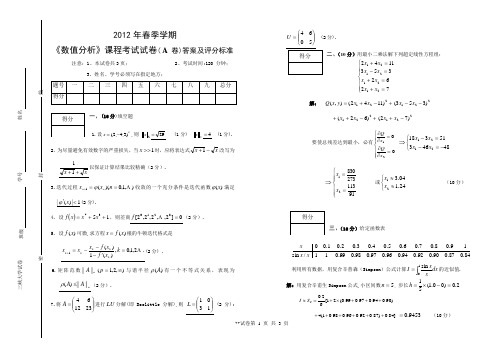
线封密三峡大学试卷班级姓名学号2012年春季学期《数值分析》课程考试试卷( A 卷)答案及评分标准注意：1、本试卷共3页；2、考试时间:120 分钟；3、姓名、学号必须写在指定地方；一、(16分)填空题1.设T x )3,4,2(-=,则 2x 29= (1分) ∞x4= (1分).2. 为尽量避免有效数字的严重损失，当1>>x 时，应将表达式x x -+1改写为xx ++11以保证计算结果比较精确（2分）.3.迭代过程),1,0)((1 ==+n x x n n ϕ收敛的一个充分条件是迭代函数)(x ϕ满足1|)(|<'x ϕ(2分).4. 设()1537++=x x x f ，则差商0]2,,2,2,2[821= f （2分）.5. 设)(x f 可微,求方程)(x f x =根的牛顿迭代格式是.2,1,0,)(1)(1='---=+k x f x f x x x k k k k k (2分) .6.矩阵范数),2,1(||||∞=p A p 与谱半径)(A ρ有一个不等式关系，表现为p A A ||||)(≤ρ（2分）.7.将⎪⎪⎭⎫ ⎝⎛=231264A 进行LU 分解(即Doolittle 分解),则 ⎪⎪⎭⎫⎝⎛=1301L (2分);⎪⎪⎭⎫ ⎝⎛=5064U (2分).二、（10分）用最小二乘法解下列超定线性方程组：⎪⎪⎩⎪⎪⎨⎧=+=+=-=+7262353114221212121x x x x x x x x 解： +-+=221)1142(),(x x y x Q 221)353(--x x+-++221)62(x x 221)72(-+x x要使总残差达到最小，必有⎪⎪⎩⎪⎪⎨⎧=∂∂=∂∂0021x Q x Q⇒⎩⎨⎧-=-=-48463513182121x x x x⇒⎪⎪⎩⎪⎪⎨⎧==9111327383021x x 或⎩⎨⎧≈≈24.104.321x x （10分）三、（10分）给定函数表84.087.090.092.094.096.097.098.099.011/sin 19.08.07.06.05.04.03.02.01.00x x x 利用所有数据，用复合辛普森（Simpson ）公式计算dxx xI ⎰=10sin 的近似值. 解: 用复合辛甫生Simpson 公式,小区间数5=n , 步长2.0)00.1(51=-⨯=h)90.094.097.099.0(21[62.05+++⨯+=≈S I]84.0)87.092.096.098.01(4++++++ 9453.0= （10分）线封密三峡大学试卷班级姓名学号四、（12分）设nn ij Ra A ⨯∈=)(对称,顺序主子式),,2,1(0n i i =≠∆则T LDL A =分解存在,其中L 为单位下三角形矩阵,D 为对角阵, 试写出求方程组b Ax =解的计算步骤(用矩阵表示), 此法称为改进平方根法. 试用它求解方程组：⎩⎨⎧=+=+635310121022121x x x x 解: 由T LDL A =可得b Ax =的方程为b x LDL T=,令y x DL T =,则b Ly =.计算步骤： (1) 将A 直接分解TLDL A =，求出 D L , (2) 求解方程b Ly =(3) 求解方程y D x L T 1-= （4分）⎢⎣⎡102 ⎥⎦⎤5310⎥⎦⎤⎢⎣⎡=10121l ⎥⎦⎤⎢⎣⎡2100d d ⎥⎦⎤⎢⎣⎡10121l 比较矩阵两边的元素,可得: ,521=l ,21=d .32=d由b Ly =可得 ⎥⎦⎤⎢⎣⎡1501⎥⎦⎤⎢⎣⎡21y y ⎥⎦⎤⎢⎣⎡=6312 ⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⇒31221y y 由y D x L T1-=得 ⎥⎦⎤⎢⎣⎡1051⎥⎦⎤⎢⎣⎡21x x ⎥⎦⎤⎢⎣⎡=16 ⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⇒1112x x （12分）五、(12分) 取节点1,010==x x ,写出x e x y -=)(的一次插值多项式),(1x L 并估计插值误差.解: 建立Lagrange 公式为 ()x L 110100101y x x x x y x x x x --+--=1101101-⨯--+⨯--=e x x x e x 11-+-=. （8分） ())1)(0(!2)()()(11--''=-=x x y x L x y x R ξ )10(<<ξ ()1)0(max 2110--≤≤≤x x x 令 ),1()(-=x x x h 由0)(='x h ，求得一个驻点得211=x于是 =≤≤|)(|max 10x h x 41)}1(),(),0({max 110=≤≤h x h h x 所以有())()(11x L x y x R -=)(max 2110x h x ≤≤≤81= （12分）六、(10分) 在区间[0,2]上利用压缩映像原理验证迭代格式1012.k x k +==，，，的敛散性. 解：(1) 记x x +=2)(ϕ，则xx +='221)(ϕ.当]2,0[∈x 时,];2,0[]2,2[)]2(),0([)(⊂=∈ϕϕϕx (5分) (2) .1221)0(|)(|<='≤'ϕϕx 因此,对]2,0[0∈∀x ,迭代格式1012.k x k +==，，，产生的序列∞=0}{k k x 收敛. (10分)线封密三峡大学试卷班级姓名学号七、（12分）已知方程组⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛121212212321x x x a a a （1）写出解此方程组的雅可比(Jacobi)迭代法公式；（2）证明当4>a 时，雅可比(Jacobi)迭代法收敛；（3）取5=a ,T x)101,51,101()0(=，求出)2(x . 解：（1）对.,3,2,1 =i 从第i 个方程解出i x ，得雅可比法迭代公式为：⎪⎪⎪⎩⎪⎪⎪⎨⎧=--=--=--=+++ ,1,0,)21(1)222(1)21(1)(2)(1)1(3)(3)(1)1(2)(3)(2)1(1n x x a x x x a x x x a x n n n n n n n n n （5分）（2）当4>a 时，A 为严格对角占优矩阵，所以雅可比迭代法收敛. （10分）（3）取5=a ，Tx )101,51,101()0(= 由迭代公式计算得 101)1(1=x ， 258)1(2=x ， 101)1(3=x . 25013)2(1=x ， 258)2(2=x ， 25013)2(3=x . （12分）八、（10分）设初值问题:⎩⎨⎧=≤≤++='0)0(10,122y x y x y , (1) 写出用Euler 方法、取步长1.0=h 解上述初值问题数值解的公式； (2) 写出用改进Euler 方法、取步长1.0=h 解上述初值问题数值解的公式. 解: （1）取步长1.0=h 解上述初值问题数值解的Euler 公式为；9,,1,0),1(1.0),(0221==++⨯+=+=+y n y x y y x hf y y n n n n n n n （5分）（2）取步长1.0=h 解上述初值问题数值解的改进Euler 公式为：)2(21.0)1(1.002121221221=⎪⎩⎪⎨⎧+++++=++⨯+=++++y y x y x y y y x y y n n n n n n n n n n （10分）九、（8分）学完《数值分析》这门课程后，请你简述一下“插值、逼近、拟合”三者的区别和联系.解: 答案略.。

2012级研究生数值分析试卷A

一．（1）已知函数24()73f x x x =++，用秦九昭方法计算(2)f ；（2）秦九昭方法计算任一n 次多项式在任一点函数值至多需要多少次乘法？（3）至少写出四种减少误差危害的常用手段。

二．给定方程组123311413132156x x x ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥-=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦ （1）以分量形式写出解此线性方程组的Jacobi 迭代格式和Gauss -Seidel 迭代格式；（2）求1A 和A ∞；（3）判断Gauss -Seidel 迭代格式的敛散性。

三．已知方程2()30x f x e x =-=，（1）证明该方程在区间[0.6,1.2]上存在唯一实根；（2）叙述牛顿法求方程()0f x =根的方法思想；（3）以初值01x =，用牛顿法求上述方程的近似解，要求误差不超过210- 。

四．（1）求012,,A A A ，使得数值求积公式20122()(2)(0)(2)f x dx A f A f A f -≈-++⎰具有尽可能高的代数精度，并求出其代数精度；（2）试用复合Simpson 公式2S 计算120sin x dx ⎰。

五．（1）叙述Newton 插值法与Lagrange 插值法的异同。

（2）对下述列表函数：写出差商表；并写出逼近上述列表函数的三次Newton 插值多项式。

六．用LU 分解法解下述方程组，并写出矩阵L 与U 。

12312312334241255x x x x x x x x x-+=⎧⎪-+=⎨⎪+-=⎩七．(1) 取步长0.1h =，完成利用改进的Euler 方法解下述初值问题的Matlab 程序, 使得输出结果yy (n +1)为下述微分方程初值问题的解函数在0.3x =处函数值(0.3)y 的近似值。

'23(0)2y x y =+⎧⎨=⎩function ex( )a=0; b=0.3; y0= ; n= ; [x,yy]=improved_euler_method(@fxy,a,b,y0,n) returnfunction z=fxy(x,y)z= ; returnfunction [x,y]=improved_euler_method(f,a,b,y0,n) h=(b-a)/n; y=zeros(1,n+1); x=a:h:b; y(1)=y0; for j=1:ntemp= ;y(j+1)=y(j)+h*temp; y(j+1)=y(j)+h*(temp+f(x(j+1),y(j+1)))/2; end return(2) 叙述求解一阶微分方程初值问题的梯形方法和改进的Euler 方法的方法思想。

2012数值分析试卷答案

##理工大学2012级硕士研究生试卷科目：数值分析考试时间：出题教师：集体考生__专业：__予计分；可带计算器.一、填空题〔每空2分,共40分〕1．设*0.231x =是真值0.228x =的近似值,则*x 有位有效数字,*x 的相对误差限为.2．设133)(47+++=x x x x f ,则=]2,,2,2[710 f ,=]2,,2,2[810 f . 3. 过点)0,2(),0,1(-和)3,1(的二次拉格朗日插值函数为)(2x L =, 并计算=)0(2L . 4．设32()3245f x x x x =+-+在[]1,1-上的最佳二次逼近多项式为,最佳二次平方逼近多项式为. 5．高斯求积公式)()()(11010x f Ax f A dx x f x +≈⎰的系数0A =,1A =,节点0x =,1x =.6．方程组b Ax =,,U L D A --=建立迭代公式f Bx xk k +=+)()1(,写出雅可比迭代法和高斯-赛德尔迭代法的迭代矩阵,=Jacobi B ,=-Seidel Gauss B .7．00100A ⎤⎥⎥=⎢⎥⎢⎥,其条件数2()Cond A =.8．设⎥⎦⎤⎢⎣⎡=2113A ,计算矩阵A 的X 数,1||||A = , 2||||A = .9．求方程()x f x =根的牛顿迭代格式是.10．对矩阵⎪⎪⎪⎭⎫ ⎝⎛=513252321A 作LU 分解,其L=________________, U= __________________.二、计算题〔每题10分,共50分〕1. 求一个次数不高于4次的多项式P <x >,使它满足:1)1(,0)0(,0)0('===p p p ,1)1(,'=p,1)2(=p 并写出其余项表达式〔要求有推导过程〕.2. 若用复合梯形公式计算积分dx e x ⎰1,问区间[0, 1]应分成多少等分才能使截断误差不超过51021-⨯? 若改用复合辛普森公式,要达到同样的精度区间[0, 1]应该分成多少等份? 由下表数据,用复合辛普森公式计算该积分的近似值.3. 线性方程组b Ax =,其中⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=18.04.08.014.04.04.01A ,T b ]3,2,1[=,〔1〕建立雅可比迭代法和高斯-赛德尔迭代法的分量形式.〔2〕问雅可比迭代法和高斯-赛德尔迭代法都收敛吗?4. 已知如下实验数据4,,1,0),,( =i y x i i , 用最小二乘法求形如x a a y 10+=的经验公式,并计算最小二乘法的误差.5.用改进的欧拉公式<预估-校正方法>,解初值问题0)0(,10022=+=y y x dx,取步长,1.0=h 计算到2.0=x〔保留到小数点后四位〕.三、证明题〔共10分〕1．如果 A 是对称正定矩阵,则A 可唯一地写成T LL A =,其中L 是具有正对角元的下三角阵.##理工大学2012级硕士研究生试卷答案一填空题〔每空2分,共40分〕1. 2 0.025或0.02162. 3 03. )2)(1(23-+-x x ,34. 2754x x -+2119255x x -+ 5. 0.28 0.39 0.29 0.826. U L D H U L D H S G J 11)(),(----=+=7. 18. | A ||1 = 3_,2316299||||2++=A9. 1()1'()k k k k k x f x x x f x +-=--10. ⎪⎪⎪⎭⎫ ⎝⎛-=153012001L ,⎪⎪⎪⎭⎫ ⎝⎛--=2400410321U二、计算题〔每空10分,共50分〕1．求一个次数不高于4次的多项式P <x >,使它满足:P <0> =0,P’<0> =0,P <1> =1,P’<1>=1,P <2> =1,并写出其余项表达式.解：由题意P <x > = x 2<ax 2 + b x + c >,由插值条件得方程组求解,得 a =1/4,b= – 3/2 ,c =9/4.所以插值余项为)2()1()(!51)(22)5(--=x x x f x R ξ2．若用复合梯形公式计算积分dx e x ⎰1,问区间[0, 1]应分成多少等分才能使截断误差不超过51021-⨯？若改用复合辛普森公式,要达到同样的精度区间[0, 1]应该分成多少等分？由下表数据用复合辛普森公式计算该积分.解：由于xe xf =)(,则x e x fx f ==)()()4(''在区间[0,1]上为单调增函数,b-a=1,设区间分成n 等分,则h=1/n., 故对复合梯形公式,要求≤--=|)(12|)(''2ηf h a b f R T 521021)1(121-⨯≤e n ,)1,0(∈η 即52106⨯≥en ,85.212≥n ,因此n=213,即将区间[0,1]分成213等分时,用复合梯形计算,截断误差不超过51021-⨯.若用复合辛普森公式,则要求≤⎪⎭⎫ ⎝⎛--=|)(2180|)(()42ηf h a b f R S 5441021)1(21801-⨯≤⨯e n,)1,0(∈η4410144⨯≥en ,7066.3≥n ,因此n=4,即将区间[0,1]分成8等分时,用复合梯形计算,截断误差不超过51021-⨯.3. 线性方程组b Ax =,其中⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=18.04.08.014.04.04.01A ,Tb ]3,2,1[=,〔1〕建立Jacobi 迭代法和Gauss-Seidel 迭代法的分量形式.〔2〕问Jacobi 迭代和Gausse-Seidel 迭代法都熟收敛吗？解：（1） Jacobi 迭代法的分量形式⎪⎩⎪⎨⎧=--=--=--=+++ ,2,1,0,)8.04.03()8.04.02()4.04.01()(2)(1)1(3)(3)(1)1(2)(3)(2)1(1k x x x x x x x x x k k k k k k k k k ,)0(x 为任意初始值. Gauss-Seidel 迭代法的分量形式⎪⎩⎪⎨⎧=--=--=--=++++++ ,2,1,0,)8.04.03()8.04.02()4.04.01()1(2)1(1)1(3)(3)1(1)1(2)(3)(2)1(1k x x x x x x x x x k k k k k k k k k ,)0(x 为任意初始值. <2>Jacobi 迭代法的迭代矩阵10928203.1)(>=J B ρ,故Jacobi 迭代法不收敛.Gauss-Seidel 迭代法的迭代矩阵18.0)(<=-S G B ρ,故G-S 迭代法收敛.4. 已知实验数据5,,2,1),,( =k y x k k ,如下表,用最小二乘法求形如x a a y 10+=的经解：令x a a x S 101)(+= 故由法方程得线性方程组解得25.1,45.210==a a 于是所求拟合曲线为 2-X 数的误差5.用改进的欧拉公式〔预估-校正方法〕解初值问题0)0(,10022=+=y y x dxdy,h 为步长,〔1〕取步长,1.0=h 计算到2.0=x 〔保留到小数点后四位〕. 解：〔1〕由改进的欧拉公式因为,1.0=h 00=y ,22100),(y x y x f += 所以2.0,1.0,0210===x x x=+=),(0001y x hf y y 0,),(),([2110001y x f y x f hy y ++==0.0005=+=),(1112y x hf y y 0.0015)],(),([2|221112.02y x f y x f hy y x ++===0.0030三、证明题〔共10分〕1、证明：如果 A 是对称正定矩阵,则A 可唯一地写成T LL A =,其中L 是具有正对角元的下三角阵.法一：因为A 对称正定,A 的所有顺序主子式不为零. A 有唯一的Doolittle 分解其中D 为对角阵,0U 为单位上三角矩阵. 又因为A 是对角正定矩阵T A A DU L ==0=TTL D U 0由分解的唯一性TU L 0=,代入分解式子又A 对称正定知道2121221122112211D D u u u u u u u u u D nn nn nn =⎪⎪⎪⎪⎪⎭⎫⎝⎛⎪⎪⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=所以TTLL D L D L A ==)(2121,其中21D L 为对角元为正的下三角矩阵.。

《数值分析》练习题及答案解析

《数值分析》练习题及答案解析第一章绪论主要考查点：有效数字，相对误差、绝对误差定义及关系；误差分类；误差控制的基本原则；。

1. 3.142和3.141分别作为π的近似数具有（）和（）位有效数字.A ．4和3B ．3和2C ．3和4D ．4和4 答案：A2. 设 2.3149541...x *=，取5位有效数字，则所得的近似值x=___________ .答案：2.31503.若近似数2*103400.0-⨯=x 的绝对误差限为5105.0-⨯,那么近似数有几位有效数字解：2*103400.0-⨯=x ，325*10211021---⨯=⨯≤-x x 故具有3位有效数字。

4 . 14159.3=π具有4位有效数字的近似值是多少？解：10314159.0⨯= π，欲使其近似值*π具有4位有效数字，必需！41*1021-⨯≤-ππ，3*310211021--⨯+≤≤⨯-πππ，即14209.314109.3*≤≤π即取（ , ）之间的任意数，都具有4位有效数字。

第二章非线性方程求根主要考查点：二分法N 步后根所在的区间，及给定精度下二分的次数计算；非线性方程一般迭代格式的构造，（局部）收敛性的判断，迭代次数计算；牛顿迭代格式构造；求收敛阶；1.用二分法求方程012=--x x 的正根，要求误差小于0.05。

（二分法）解：1)(2--=x x x f ，01)0(<-=f ，01)2(>=f ，)(x f 在[0，2]连续，故[0，2]为函数的有根区间。

"（1）计算01)1(<-=f ，故有根区间为[1，2]。

（2）计算041123)23()23(2<-=--=f ，故有根区间为]2,23[。

（3）计算0165147)47()47(2>=--=f ，故有根区间为]47,23[。

（4）计算06411813)813()813(2>=--=f ，故有根区间为]813,23[。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

研究生考试命题纸
沈阳工业大学 2012 / 2013 学年第一学期
课程名称：数值分析课程编号：000304 任课教师：陈欣曲绍波考试形式：闭卷
一、填空（每题3分，共15分）
1. 二分法是求解方程f (x )=0的根一种方法，其前提是f (x )在有根区间[a ,b ]内单调且。

2. 设矩阵⎪⎪⎭
⎫ ⎝⎛-=0112A ，则1A = 、=2A 、)(A ρ= 。

3. 对于正数a ，使用牛顿法于方程02=-a x 所得到的迭代格式为，其收敛阶为、求110（取x 0=10）的第一个近似值为。

4. 幂法用来计算实矩阵A 的特征值及对应的，在计算过程中进行“归一化”处理的原因是为了。

5. 高斯求积公式)3
3()33()(11f f dx x f +-≈⎰-的代数精度为，当区间不是[-1,1]，而是一般区间[a , b ]时，需要做变换，使用该公式计算≈⎰311dx x。

二、解答下列各题（每题5分，共10分）
1. 请写出经过点A (0,1)，B (2,3)，C (4,5)的拉格朗日插值多项式形式。

说明插值基函数的性质以及拉格朗日插值法的优缺点。

2. 设n 阶可逆矩阵A 已经分解成A =LU ，其中L 下三角矩阵，U 单位上三角矩阵，推导出解线性方程组AX =b 的计算公式。

三、（10分）用不选主元的直接三角分解法解下面线性方程组
⎪⎪⎩⎪⎪⎨⎧=+-=-+-=-+-=-3
424243443432
32121x x x x x x x x x x 四、（20分，每题10分）对于线性方程组⎪⎩⎪⎨⎧=++=++=-+9223122321
321321x x x x x x x x x 1. 分别写出使用GS 迭代法，SOR 迭代法（ω=1.3）求解的迭代格式，并对初始向量（1，0，0）T ，分别计算第一步近似解向量；
2. 分别讨论求解此方程的J —方法和GS —方法的收敛性。

五、（10分）给出函数表如下，用牛顿向前插值公式求f (2.03)的近似值。

x 2.0 2.1 2.2 2.3 2.4 （误差限10－3） y 1.41421 1.44914 1.48324 1.51658 1.54919
六、（10分）对下列数据，用最小二乘法求形如指数函数y = a e bx 的经验公式。

（保留4位小数）
x i 1.0 2.0 3.0 4.0 5.0
y i 33.40 122.65 189.15 238.65 267.55
七、（10分）取步长h =0.2，分别用改进欧拉法、四阶龙格-库塔方法求解初值
问题
⎩⎨⎧=-=1
)0(xy 2'y y ，0≤x ≤0.2 八、（7分）设A ∈R n ×n 为一个非奇异矩阵，x 为R n 中的任意向量范数，试证
Ax x A =是R n 中的一个向量范数。

九、（8分）证明迭代公式a x a x x x k k k k ++=+221
3)3(是计算a 的三阶方法。