东南大学计算方法与实习上机实验三
计算方法B上机报告

计算方法B上机实习报告计算方法B 上机实习报告1.对以下和式计算:0142118184858616n n S n n n n ∞=⎛⎫=--- ⎪++++⎝⎭∑,要求: (1)若只需保留11个有效数字,该如何进行计算;(2)若要保留30个有效数字,则又将如何进行计算;问题分析:在该题中S 的每一项14211()1681848586n ns n n n n =---++++存在两个相近的数相减的问题,因此为了避免有效数字损失,最好是改变运算顺序,分别将正数和负数相加,然后再将其和相加。
另外,sn 中有多个负数相加,可以按照绝对值递增的顺序求和,以减少舍入误差的影响。
同时,为了避免大数吃小数的问题,本题先计算出保留目标有效数字所需 要的迭代次数,然后采用倒序相加的方法实现。
程序实现:clear;clc;m=input('请输入要保留的有效数字位数:'); s1=0; s2=0; k=0; s=1;%%%%判断多需要的迭代次数 while s>=0.5*10^-(m-1)s=4/(16^k*(8*k+1))-(2/(16^k*(8*k+4))+1/(16^k*(8*k+5))+1/(16^k*(8*k+6))); k=k+1; end%%%%正负数分别按照绝对值递增的顺序倒序相加 for n=(k-1):-1:0 a1=4/(16^n*(8*n+1)); a2=2/(16^n*(8*n+4)); a3=1/(16^n*(8*n+5)); a4=1/(16^n*(8*n+6)); s1=a1+s1; s2=a4+a3+a2+s2; end S=s1-s2; S=vpa(S,m)运算结果:总结心得:在计算求和问题中,应特别注意相近数相减的问题,这样会造成有效数字灾难性的损失。
另外在两个数量级相差较大的数字相加减时,较小数的有效数字会被丧失,因此要按照从小到大的顺序相加。
在上题计算中分别对正负相采用倒序相加,这样就有效的避免了“大数吃小数”的问题。
计算方法上机报告_董晓壮

计算方法A上机报告学院(系):电气工程学院学生姓名:陶然学号:授课老师:完成日期:2019年12月03日西安交通大学Xi'an Jiaotong University目录1 QR分解法求解线性方程组 (2)1.1 算法原理 (2)1.1.1 基于吉文斯变换的QR分解 (2)1.1.2 基于豪斯霍尔德变换的QR分解 (3)1.2 程序流程图 (4)1.2.1 基于吉文斯变换的QR分解流程图 (4)1.2.2 基于豪斯霍尔德变换的QR分解流程图 (5)1.3 程序使用说明 (5)1.3.1 基于吉文斯变换的QR分解程序说明 (5)1.3.2 基于豪斯霍尔德变换的QR分解程序说明 (7)1.4 算例计算结果 (8)2 共轭梯度法求解线性方程组 (10)2.1 算法原理 (10)2.2 程序流程图 (10)2.3 程序使用说明 (11)2.4 算例计算结果 (12)3 三次样条插值 (14)3.1 算法原理 (14)3.2 程序流程图 (16)3.3 程序使用说明 (17)3.4 算例计算结果 (19)4 龙贝格积分 (21)4.1 算法原理 (21)4.2 程序流程图 (22)4.3 程序使用说明 (23)4.4 算例计算结果 (24)结论 (26)1 QR 分解法求解线性方程组1.1 算法原理矩阵的QR 分解是指,可以将矩阵A 分解为一个正交矩阵Q 和一个上三角矩阵R 的乘积,实际中,QR 分解经常被用来解决线性最小二乘问题,分解情况如图1.1所示。
=⨯图1.1 QR 分解示意图本次上机学习主要进行了两个最基本的正交变换—吉文斯(Givens )变换和豪斯霍尔德(Householder )变换,并由此导出矩阵的QR 分解以及求解线性方程组的的方法。
1.1.1 基于吉文斯变换的QR 分解吉文斯矩阵也称初等旋转阵,如式(1.1)所示,它把n 阶单位矩阵I 的第,i j 行的对角元改为c ,将第i 行第j 列的元素改为s ,第j 行第i 列的元素改为s −后形成的矩阵。
(完整word版)计算方法A上机实验报告

计算方法A上机实验报告姓名:苏福班级:硕4020 学号:3114161019一、上机练习目的1)复习和巩固数值计算方法的基本数学模型,全面掌握运用计算机进行数值计算的具体过程及相关问题。
2)利用计算机语言独立编写、调试数值计算方法程序,培养学生利用计算机和所学理论知识分析解决实际问题的能力。
二、上机练习任务1)利用计算机语言编写并调试一系列数值方法计算通用程序,并能正确计算给定题目,掌握调试技能。
2)掌握文件使用编程技能,如文件的各类操作,数据格式设计、通用程序运行过程中文件输入输出运行方式设计等。
3)写出上机练习报告。
三、上机题目1. 共轭梯度法求解线性方程组。
(第三章)2. 三次样条插值(第四章)3. 龙贝格积分(第六章)4. 四阶龙格-库塔法求解常微分方程的初值问题四、上机报告题目1:共轭梯度法求解线性方程组1.算法原理共轭梯度法是把求解线性方程组的问题转化为求解一个与之等价的二次函数极小值的问题。
从任意给定的初始点出发,沿一组关于矩阵A共轭的方向进行线性搜索,在无舍入误差的假定下,最多迭代n 次(其中n 为矩阵A 的阶数),就可求得二次函数的极小值,也就求得了线性方程组Ax b =的解。
定理:设A 是n 阶对称正定矩阵,则x *是方程组Ax b =的解得充分必要条件是x *是二次函数1()2TT f x x Ax b x =-的极小点,即 ()()min nx R Ax b f x f x **∈=⇔=共轭梯度法的计算公式:(0)(0)(0)()()()()(1)()()(1)(1)(1)()()()(1)(1)()k T k k k T k k k k k k k k T k k k T k k k k k d r b Ax r d d Ad xx d r b Ax r Ad d Ad d r d ααββ++++++⎧==-⎪⎪=⎪⎪=+⎪⎨=-⎪⎪⎪=-⎪⎪=+⎩2. 程序框图(1)编写共轭梯度法求解对称正定矩阵的线性方程组见附录(myge.m):function x=myge(A,b)输入对称正定矩阵及对应的列向量,初始向量设为0,精度取为810 。
计算方法上机实验

1.拉格朗日插值多项式,用于离散数据的拟合#include <stdio.h>#include <conio.h>#include <alloc.h>float lagrange(float *x,float *y,float xx,int n) /*拉格朗日插值算法*/{ int i,j;float *a,yy=0.0; /*a作为临时变量,记录拉格朗日插值多项式*/a=(float *)malloc(n*sizeof(float));for(i=0;i<=n-1;i++){ a[i]=y[i];for(j=0;j<=n-1;j++)if(j!=i) a[i]*=(xx-x[j])/(x[i]-x[j]);yy+=a[i];}free(a);return yy;}main(){ int i,n;float x[20],y[20],xx,yy;printf("Input n:");scanf("%d",&n);if(n>=20) {printf("Error!The value of n must in (0,20)."); getch();return 1;} if(n<=0) {printf("Error! The value of n must in (0,20)."); getch(); return 1;} for(i=0;i<=n-1;i++){ printf("x[%d]:",i);scanf("%f",&x[i]);}printf("\n");for(i=0;i<=n-1;i++){ printf("y[%d]:",i);scanf("%f",&y[i]);}printf("\n");printf("Input xx:");scanf("%f",&xx);yy=lagrange(x,y,xx,n);printf("x=%f,y=%f\n",xx,yy);getch();}2.牛顿插值多项式,用于离散数据的拟合#include <stdio.h>#include <conio.h>#include <alloc.h>void difference(float *x,float *y,int n){ float *f;int k,i;f=(float *)malloc(n*sizeof(float));for(k=1;k<=n;k++){ f[0]=y[k];for(i=0;i<k;i++)f[i+1]=(f[i]-y[i])/(x[k]-x[i]);y[k]=f[k];}return;}main(){ int i,n;float x[20],y[20],xx,yy;printf("Input n:");scanf("%d",&n);if(n>=20) {printf("Error! The value of n must in (0,20)."); getch(); return 1;} if(n<=0) {printf("Error! The value of n must in (0,20).");getch(); return 1;} for(i=0;i<=n-1;i++){ printf("x[%d]:",i);scanf("%f",&x[i]);}printf("\n");for(i=0;i<=n-1;i++){ printf("y[%d]:",i);scanf("%f",&y[i]);}printf("\n");difference(x,(float *)y,n);printf("Input xx:");scanf("%f",&xx);yy=y[20];for(i=n-1;i>=0;i--) yy=yy*(xx-x[i])+y[i];printf("NewtonInter(%f)=%f",xx,yy);getch();}3.高斯列主元消去法,求解其次线性方程组第一种#include<stdio.h>#include <math.h>#define N 20int main(){ int n,i,j,k;int mi,tmp,mx;float a[N][N],b[N],x[N];printf("\nInput n:");scanf("%d",&n);if(n>N){ printf("The input n should in(0,N)!\n");getch();return 1;}if(n<=0){ printf("The input n should in(0,N)!\n");getch();return 1;}printf("Now input a(i,j),i,j=0...%d:\n",n-1); for(i=0;i<n;i++){ for(j=0;j<n;j++)scanf("%f",&a[i][j]);}printf("Now input b(i),i,j=0...%d:\n",n-1);for(i=0;i<n;i++)scanf("%f",&b[i]);for(i=0;i<n-2;i++){ for(j=i+1,mi=i,mx=fabs(a[i][j]);j<n-1;j++) if(fabs(a[j][i])>mx){ mi=j;mx=fabs(a[j][i]);}if(i<mi){ tmp=b[i];b[i]=b[mi];b[mi]=tmp;for(j=i;j<n;j++){ tmp=a[i][j];a[i][j]=a[mi][j];a[mi][j]=tmp;}}for(j=i+1;j<n;j++){ tmp=-a[j][i]/a[i][i];b[j]+=b[i]*tmp;for(k=i;k<n;k++)a[j][k]+=a[i][k]*tmp;}}x[n-1]=b[n-1]/a[n-1][n-1];for(i=n-2;i>=0;i--){ x[i]=b[i];for(j=i+1;j<n;j++)x[i]-=a[i][j]*x[j];x[i]/=a[i][i];}for(i=0;i<n;i++)printf("Answer:\n x[%d]=%f\n",i,x[i]); getch();return 0;}第二种#include<math.h>#include<stdio.h>#define NUMBER 20#define Esc 0x1b#define Enter 0x0dfloat A[NUMBER][NUMBER+1] ,ark;int flag,n;exchange(int r,int k);float max(int k);message();main(){float x[NUMBER];int r,k,i,j;char celect;clrscr();printf("\n\nUse Gauss.");printf("\n\n1.Jie please press Enter."); printf("\n\n2.Exit press Esc.");celect=getch();if(celect==Esc)exit(0);printf("\n\n input n=");scanf("%d",&n);printf(" \n\nInput matrix A and B:"); for(i=1;i<=n;i++){printf("\n\nInput a%d1--a%d%d and b%d:",i,i,n,i);for(j=1;j<=n+1;j++) scanf("%f",&A[i][j]);}for(k=1;k<=n-1;k++){ark=max(k);if(ark==0){printf("\n\nIt's wrong!");message();}else if(flag!=k)exchange(flag,k);for(i=k+1;i<=n;i++)for(j=k+1;j<=n+1;j++)A[i][j]=A[i][j]-A[k][j]*A[i][k]/A[k][k];}x[n]=A[n][n+1]/A[n][n];for( k=n-1;k>=1;k--){float me=0;for(j=k+1;j<=n;j++){me=me+A[k][j]*x[j];}x[k]=(A[k][n+1]-me)/A[k][k];}for(i=1;i<=n;i++){printf(" \n\nx%d=%f",i,x[i]);}message();}exchange(int r,int k){int i;for(i=1;i<=n+1;i++)A[0][i]=A[r][i];for(i=1;i<=n+1;i++)A[r][i]=A[k][i];for(i=1;i<=n+1;i++)A[k][i]=A[0][i];}float max(int k){int i;float temp=0;for(i=k;i<=n;i++)if(fabs(A[i][k])>temp){temp=fabs(A[i][k]);flag=i;}return temp;}message(){printf("\n\n Go on Enter ,Exit press Esc!");switch(getch()){case Enter: main();case Esc: exit(0);default:{printf("\n\nInput error!");message();} }}4.龙贝格求积公式,求解定积分#include<stdio.h>#include<math.h>#define f(x) (sin(x)/x)#define N 20#define MAX 20#define a 2#define b 4#define e 0.00001float LBG(float p,float q,int n){ int i;float sum=0,h=(q-p)/n;for (i=1;i<n;i++)sum+=f(p+i*h);sum+=(f(p)+f(q))/2;return(h*sum);}void main(){ int i;int n=N,m=0;float T[MAX+1][2];T[0][1]=LBG(a,b,n);n*=2;for(m=1;m<MAX;m++){ for(i=0;i<m;i++)T[i][0]=T[i][1];T[0][1]=LBG(a,b,n);n*=2;for(i=1;i<=m;i++)T[i][1]=T[i-1][1]+(T[i-1][1]-T[i-1][0])/(pow(2,2*m)-1);if((T[m-1][1]<T[m][1]+e)&&(T[m-1][1]>T[m][1]-e)){ printf("Answer=%f\n",T[m][1]); getch();return ;}}}5.牛顿迭代公式,求方程的近似解#include<stdio.h>#include<math.h>#include<conio.h>#define N 100#define PS 1e-5#define TA 1e-5float Newton(float (*f)(float),float(*f1)(float),float x0 ) { float x1,d=0;int k=0;do{ x1= x0-f(x0)/f1(x0);if((k++>N)||(fabs(f1(x1))<PS)){ printf("\nFailed!");getch();exit();}d=(fabs(x1)<1?x1-x0:(x1-x0)/x1);x0=x1;printf("x(%d)=%f\n",k,x0);}while((fabs(d))>PS&&fabs(f(x1))>TA) ;return x1;}float f(float x){ return x*x*x+x*x-3*x-3; }float f1(float x){ return 3.0*x*x+2*x-3; }void main(){ float f(float);float f1(float);float x0,y0;printf("Input x0: ");scanf("%f",&x0);printf("x(0)=%f\n",x0);y0=Newton(f,f1,x0);printf("\nThe root is x=%f\n",y0); getch();}。
计算方法与实习 第四版 (孙志忠 著) 东南大学出版社 课后答案

2
ww
w.
kh
da
w.
co
∗ − y | → ∞, 计算过程不稳定。 注 :此题中,|yn n
m
× 10−3 .
w.
n = 1, 2, · · ·
co m
e2 e2 r r = . 1 + er 1 − er
w.
课后答案网
aw . kh d
∗ − y | = 510 e ≤ n = 10时,|yn n 0
√ 计算到y100 , 若取 783 ≈ 27.982 (5位有效数字),试问计算到y100 将有多大误差? √ 答 :设x∗ = 783, x = 27.982, x∗ = x + e.
−2 ∗ = y∗ yn n−1 − 10 (x + e), yn = yn−1 − 10−2 x,
1 √ 783, 100
概率与数理统计 第二, C语言程序设计教程 第 西方经济学(微观部分) C语言程序设计教程 第 复变函数全解及导学[西 三版 (浙江大学 三版 (谭浩强 张 (高鸿业 著) 中 二版 (谭浩强 张 安交大 第四版]
社区服务
社区热点
进入社区
/
2009-10-15
ww
er − er = er −
e2 e e 1 r = . = e − = e − r r x∗ e+x 1 + er 1 + e1 r ·········
7. 设y0 = 28, 按递推公式
案 答
yn = yn−1 −
网 课 后
1 2
6. 机器数–略。
w. kh da
∗ −y |=e≤ n = 100时,|yn n
课后答案网
东南大学计算机网络第三次实验报告

东南大学自动化学院实验报告课程名称:信息通信网络概论第3次实验实验名称:实验三基于客户/服务器模式的网络通信编程实现院(系):自动化专业:自动化姓名:学号:实验室:金智楼实验组别:同组人员:实验时间: 2016 年 12 月 13 日评定成绩:审阅教师:目录一.实验目的和要求 (3)二.实验原理 (3)三. 实验方案与实验步骤 (4)四.实验设备与器材配置 (5)五.实验记录 (5)六.实验总结 (10)七.思考题或讨论题 (11)附录:部分代码一.实验目的和要求1.进一步了解网络编程的过程;2.掌握Windows环境下基于WinSock的编程方法和通信实现;3.熟悉客户/服务器模式的网络通信编程实现,编写一个聊天工具,即以客户端和服务器端的模式进行互发消息。
二.实验原理一个在建立分布式应用时最常用的范例便是客户机/服务器模型。
在这种方案中客户应用程序向服务器程序请求服务。
这种方式隐含了在建立客户机/服务器间通讯时的非对称性。
客户机/服务器模型工作时要求有一套为客户机和服务器所共识的惯例来保证服务能够被提供(或被接受)。
这一套惯例包含了一套协议。
它必须在通讯的两头都被实现。
根据不同的实际情况,协议可能是对称的或是非对称的。
在对称的协议中,每一方都有可能扮演主从角色;在非对称协议中,一方被不可改变地认为是主机,而另一方则是从机。
一个对称协议的例子是Internet中用于终端仿真的TELNET。
而非对称协议的例子是Internet中的FTP。
无论具体的协议是对称的或是非对称的,当服务被提供时必然存在“客户进程”和“服务进程”。
一个服务程序通常在一个众所周知的地址监听对服务的请求,也就是说,服务进程一直处于休眠状态,直到一个客户对这个服务的地址提出了连接请求。
在这个时刻,服务程序被“惊醒”并且为客户提供服务-对客户的请求作出适当的反应。
这一请求/相应的过程可以简单的用图2-1表示。
虽然基于连接的服务是设计客户机/服务器应用程序时的标准,但有些服务也是可以通过数据报套接口提供的。
《数值计算方法》上机实验报告

《数值计算方法》上机实验报告华北电力大学实验名称数值il•算方法》上机实验课程名称数值计算方法专业班级:电力实08学生姓名:李超然学号:200801001008 成绩: 指导教师:郝育黔老师实验日期:2010年04月华北电力大学实验报告数值计算方法上机实验报吿一.各算法的算法原理及计算机程序框图1、牛顿法求解非线性方程*对于非线性方程,若已知根的一个近似值,将在处展开成一阶xxfx ()0, fx ()xkk泰勒公式"f 0 / 2 八八,fxfxfxxxxx 0 0 0 0 0 kkkk2!忽略高次项,有,fxfxfxxx 0 ()()(),,, kkk右端是直线方程,用这个直线方程来近似非线性方程。
将非线性方程的**根代入,即fx ()0, X ,* fxfxxx 0 0 0 0, ,, kkkfx 0 fx 0 0,解出fX 0 *k XX,, k' fx 0 k水将右端取为,则是比更接近于的近似值,即xxxxk, Ik, Ikfx ()k 八XX, Ikk* fx()k这就是牛顿迭代公式。
,2,计算机程序框图:,见,,3,输入变量、输出变量说明:X输入变量:迭代初值,迭代精度,迭代最大次数,\0输出变量:当前迭代次数,当前迭代值xkl,4,具体算例及求解结果:2/16华北电力大学实验报吿开始读入l>k/fx()0?,0fx 0 Oxx,,01* fx ()0XX,,,?10kk, ,1,kN, ?xx, 10输出迭代输出X输出奇异标志1失败标志,3,输入变量、输出变量说明: 结束例:导出计算的牛顿迭代公式,并il •算。
(课本P39例2-16) 115cc (0), 求解结果:10. 75000010.72383710. 72380510. 7238052、列主元素消去法求解线性方程组,1,算法原理:高斯消去法是利用现行方程组初等变换中的一种变换,即用一个不为零的数乘 -个 方程后加只另一个方程,使方程组变成同解的上三角方程组,然后再自下而上 对上三角3/16华北电力大学实验报告方程组求解。
东南大学计算方法上机报告实验报告完整版
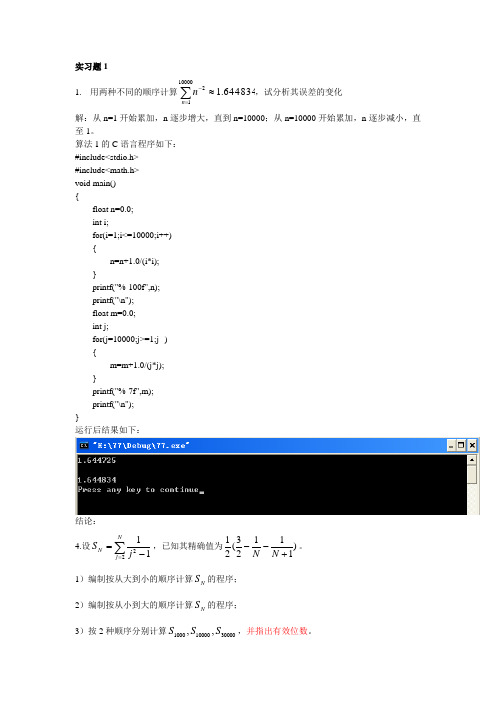
实习题11. 用两种不同的顺序计算644834.11000012≈∑=-n n,试分析其误差的变化解:从n=1开始累加,n 逐步增大,直到n=10000;从n=10000开始累加,n 逐步减小,直至1。
算法1的C 语言程序如下: #include<stdio.h> #include<math.h> void main() { float n=0.0; int i; for(i=1;i<=10000;i++) { n=n+1.0/(i*i); } printf("%-100f",n); printf("\n"); float m=0.0; int j; for(j=10000;j>=1;j--) { m=m+1.0/(j*j); } printf("%-7f",m); printf("\n"); }运行后结果如下:结论: 4.设∑=-=Nj N j S 2211,已知其精确值为)11123(21+--N N 。
1)编制按从大到小的顺序计算N S 的程序; 2)编制按从小到大的顺序计算N S 的程序;3)按2种顺序分别计算30000100001000,,S S S ,并指出有效位数。
解:1)从大到小的C语言算法如下:#include<stdio.h>#include<math.h>#include<iostream>using namespace std;void main(){float n=0.0;int i;int N;cout<<"Please input N"<<endl;cin>>N;for(i=N;i>1;i--){n=n+1.0/(i*i-1);N=N-1;}printf("%-100f",n);printf("\n");}执行后结果为:N=2时,运行结果为:N=3时,运行结果为:N=100时,运行结果为:N=4000时,运行结果为:2)从小到大的C语言算法如下:#include<stdio.h>#include<math.h>#include<iostream>using namespace std;void main(){float n=0.0;int i;int N;cout<<"Please input N"<<endl;cin>>N;for(i=2;i<=N;i++){n=n+1.0/(i*i-1);}printf("%-100f",n);printf("\n");}执行后结果为:N=2时,运行结果为:N=3时,运行结果为:N=100时,运行结果为:N=4000时,运行结果为:结论:通过比较可知:N 的值较小时两种算法的运算结果相差不大,但随着N 的逐渐增大,两种算法的运行结果相差越来越大。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
}
else{
w[i]*=XS[i]/(h*jc);
}
}
W+=w[i];
}
P=lx*W;
return P;
}
运行结果代码:
void main(){
int a=0,b=0;
clock_t start1,start2,end1,end2;
double duration1,duration2;
cout<<"所用时间为:"<<duration1<<endl;
start2=clock();
do{
b++;
BL1=BarycentricLagrange(x1,y1,xx1,4);
}while(b<=100000);
end2=clock();
duration2=(double)(end2-start2)/CLOCKS_PER_SEC;
int i,j;
float lx=1,*w,*L,W=0;
w=new float [n];
L=new float [n];
float P=0;
for(i=0;i<n;i++){//多项式l(x)=(x-x0)(x-x1)…(x-xn)
lx*=xx-x[i];
}
for(i=0;i<n;i++){//将1/(x-xj)看做一个整体L()
经过验证,即
此时该均匀节点重新定义的ωj与之前定义的ωj值相同,验证为正确定义。
算法:
3输入xi,yi(i=0,1,2,…,n),令Ln(x)=0;
4对i=1,2,…,n计算
算法程序代码:
#include<iostream>
#include<cmath>
#include<ctime>
#include<iomanip>
在关于稳定性的取值时
在初值+0.0001/rand()取微小量,
可以得出:
则得出该方法的稳定性良好。
通过该程序对该算法的验证,可以看出修正后的拉格朗日插值多项式比拉格朗日基本插值多项式计算量较小,稳定性良好,并且均匀节点时算法也具有这样的优点。
lx*=xx-x[i];
}
for(i=0;i<n-1;i++){//计算(n-1)!
jc*=n-(i+1);
}
for(i=0;i<n;i++){//将1/(x-xj)看做一个整体L()
L[i]=1/(xx-x[i]);
}
for(i=1;i<n;i++){//(n-1)(n-2)…(n-i)/i
xs*=(float)(n-i)/i;
L[i]=1/(xx-x[i]);
}
for(i=0;i<n;i++){
w[i]=L[i]*y[i];
for(j=0;j<n;j++){
if(j!=i){
w[i]*=1/(x[i]-x[j]);
}
}
W+=w[i];
}
P=lx*W;
return P;
}
对比拉格朗日基本表达式算法情况:
#include<iostream>
#include<cmath>
#include<ctime>
#include<iomanip>
#include<cstdlib>
using namespace std;
float Lagrange(float x[],float y[],float xx,int n){
int i,j;
float *l,L=0;
float y2[5]={1.2222,1.2681,1.3033,1.3293};
float xx2=0.45,BL2,ACBL;
start1=clock();
do{
a++;
L=Lagrange(x1,y1,xx1,4);
}while(a<=100000);
end1=clock();
duration1=(double)(end1-start1)/CLOCKS_PER_SEC;
XS[i]=xs;
}
h=pow(h,n-1);
for(i=0;i<n;i++){
w[i]=L[i]*y[i];
if((n-i)%2==0){
if(i==0){
w[i]*=(-1)/(h*jc);
}ቤተ መጻሕፍቲ ባይዱ
else{
w[i]*=(-1)*XS[i]/(h*jc);
}
}
else if((n-i)%2!=0){
if(i==0){
#include<cstdlib>
using namespace std;
float CorrctAverageCodeBarycentricLagrange(float x0,float y[],float xx,int n,float h){
int i,k=0;
float lx=1,jc=1,xs=1,*x,*w,*L,*XS,W=0;
x=new float [n];
w=new float [n];
L=new float [n];
XS=new float [n];
float P=0;
for(i=0;i<n;i++){//给x[i]赋值
x[i]=x0+i*h;
}
for(i=0;i<n;i++){//多项式l(x)=(x-x0)(x-x1)…(x-xn)
2对i=1,2,…,n计算
算法程序代码:
#include<iostream>
#include<cmath>
#include<ctime>
#include<iomanip>
#include<cstdlib>
using namespace std;
float BarycentricLagrange(float x[],float y[],float xx,int n){
解析:
1)对Lagrange插值多项式稍作修改:
运用多项式
可以将拉格朗日基本多项式重新写为:
令 ,
则
则它的优点是当插值点的个数增加一个时,每个ωj都除以(xj-xn+1),就可以得到新的ωn+1,则计算的工作量O(n),比重新计算每个多项式所需要的复杂度O(n2)减少了一个量级。
算法:
1输入xi,yi(i=0,1,2,…,n),令Ln(x)=0;
cout<<"所用时间为:"<<duration2<<endl;
BL2=BarycentricLagrange(x2,y2,xx2,4);
ACBL=CorrctAverageCodeBarycentricLagrange(0.3,y2,xx2,4,0.1);
cout<<"x="<<setprecision(6)<<xx1<<", L[4]="<<setprecision(7)<<L<<endl;
}
运行结果:
3)实验分析:
利用for循环将拉格朗日基本插值多项式和修正后的拉格朗日插值多项式循环了10万次,通过程序运行如图可以看到分别所用时间为0.22ms和0.248ms,则每个程序所用时间为0.22*10-8s和0.248*10-8s。利用多次计算,得到多次所用时间数据,取平均值
则可以发现修正后的插值多项式比基本多项式运行速度更快一点。另外由于代码段事实上调用进行运算时修正所要经过的循环比基本多,仍能跟基本持平,甚至更快,所以该方法所需要的运算量更快。
float x1[5]={0.4,0.55,0.65,0.8,0.9};//非均匀节点测试
float y1[5]={0.41075,0.57815,0.69675,0.88811,1.02652};
float xx1=0.596,L,BL1;
float x2[4]={0.3,0.4,0.5,0.6};//均匀节点测试
cout<<"x="<<setprecision(6)<<xx1<<", BL1[4]="<<setprecision(7)<<BL1<<endl;
cout<<"x="<<setprecision(6)<<xx2<<", BL2[4]="<<setprecision(7)<<BL2<<endl;
cout<<"x="<<setprecision(6)<<xx2<<", ACBL[4]="<<setprecision(7)<<ACBL<<endl;
东南大学计算方法与实习
实验报告
学院:电子科学与工程学院
学号:06A12528
姓名:陈毓锋
同组人员:罗关生,肖洋
指导老师:李元庆
1、Lagrange插值多项式的表达式为:
