非负数的性质与应用优选稿
合集下载
非负数及其应用
(
)(
)
= −5+ 2 6
(第四届“希望杯”全国数学邀请赛初二第一试试题） 第四届“希望杯”全国数学邀请赛初二第一试试题） 第四届
[例3]
2u − v v − 2u 解： Q ≥ 0, ≥ 0. 4 u + 3v 4 u + 3v
∴ 2 u − v = 0. 即v = 2u.
v − 2u 3 2u − v 若u、、满足v = + + ， 4u + 3v 4u + 3v 2 2 2 求u − uv + v 的值.
定理
定理2 如果两个图形关于某直线对称，那么对称 如果两个图形关于某直线对称， 定理 轴是对称点连线的垂直平分线。 轴是对称点连线的垂直平分线。 定理3 两个图形关于某直线对称，如果它们的对 两个图形关于某直线对称， 定理 称直线或延长线相交，那么交点在对称轴上。 称直线或延长线相交，那么交点在对称轴上。
(
)
则 a − b ＞0.
2
(
( )
2
−2 a • b +
)
( )
b = −
2
(
a− b .
)
2
2
2 ab − a − b = =
( − a) + 2 − a ( − a + − b)
2 2
−b + −b
( )
2
Hale Waihona Puke = − a + −b.
(1997年重庆市初中数学竞赛决赛试题） 年重庆市初中数学竞赛决赛试题） 年重庆市初中数学竞赛决赛试题
[例2] 已知
解： Q
b a−b−2 3 +(a+b−2 2) =0,求 的值 。 a
非负数
第一讲 非负数内容提要1. 非负数的意义：在实数集合里，正数和零称为非负数.a 是非负数，可记作0a ≥,读作a 大于或等于零，即a 不小于零.2. 初中学过的几种非负数：⑴实数的绝对值是非负数. 若a 是实数，则a ≥0.⑵实数的偶数次幂是非负数. 若a 是实数，则2na ≥0（n 是正整数）.⑶算术平方根是非负数，且被开方数也是非负数. 若a 是二次根式，则a ≥0， a ≥0.⑷一元二次方程有实数根时，根的判别式是非负数，反过来也成立.若二次方程20ax bx c ++= (0a ≠)有两个实数根， 则240b ac -≥. 若240b ac -≥ (0a ≠)， 则二次方程20ax bx c ++=有两个实数根.⑸数轴上，原点和它的右边所表示的数是非负数，几何中的距离，图形中的线段、面积、体积的量数也都是非负数.3. 非负数的性质：⑴非负数集合里，有一个最小值，它就是零.例如：2a 有最小值0（当a=0时）， 1+x 也有最小值0（当1x =-时）. ⑵如果一个数和它的相反数都是非负数，则这个数就是零.若0a ≥且0a -≥，则0a =；如果0a b -≥且0b a -≥，那么0a b -=.⑶有限个非负数的和或积仍是非负数.例如：若,,a b x 都是实数数，则220a b +≥,||||0a b ⨯≥,a ≥0. ⑷若几个非负数的和等于零，则每一个非负数也都只能是零.例如若21(3)0a b -++= 那么⎪⎪⎩⎪⎪⎨⎧=+=+=-0120)3(012c b a 即⎪⎩⎪⎨⎧=+=+=-0120301c b a ∴⎪⎩⎪⎨⎧-=-==5.031c b a .例题例1.求证：方程423260x x x +++=没有实数根例2.a 取什么值时，根式)1)(2()1)(2(a a a a --+--有意义？例3. 要使等式21(2)034x x -+=-成立，x 的值是＿＿＿＿.例4 把根号外因式移到根号里：① -＿＿＿， ②=＿＿＿＿， ③-=＿＿＿＿. 练习1. 已知在实数集合里x x -+-33有意义，则x =____.2. 要使不等式2(1)0a +≤成立，实数a = _____.3. 已知1212+++-b b a ＝0，则a =＿＿, b =＿＿, 100101a b = ____.4.如果a b <,那么)()(3b x a x ++-等于（ ）（A ）(x a +. (B) (x a +.(C) (x a -+ (D) (x a -+.5．已知a 是实数且使=x , 则x =＿＿＿＿.6. 已知,a b 是实数且a 2111+-+-≤b b .=＿.7 已知：,141=-+-c a 且a -1,4-c 都是整数.求,a c 的值.8. 求方程2222640x y x y xy ++++=的实数解.9. 求适合不等式22244440x xy y x ++-+≤的未知数x 的值.10. 比较222a b c ++与ab bc ca ++的大小.11.已知方程组⎪⎩⎪⎨⎧-=+-=++=++a z xy a xz yz xy z y x 112的解,,x y z 都是非负数. 求a 的值.。
数学2020年春季人教版教案 7年级-4 非负数的性质及应用
整理得｜b+2｜+ +(a-c)²=6-2a.
根据非负数的性质可知6-2a≥0，得a≤3，
∴a=3.
∴｜b+2｜ +(3-c)²=0，
∴ 解得 ∴a-b+c=8.
综上,a-b+c=4或8.
3.学生再次汇报，教师点评.
4.教师小结：
师：非负数有如下性质：（1）有限个非负数之和为非负数；（2）非负数与正数之和为正数；（3）若有限个非负数的和为零，则每个非负数都为0.
3.几个非负数的和或积一定是非负数.
4.若几个非负数的和为0，则每一个非负数也都只能为0.
课后反思：
本讲教材及练习册答案：
类似性问题：
1. B
2. B
3. C
4. 解：由｜y-x｜=x-y,知x≥y.
又∵｜x｜= ,∴x= 或- .∵y是3的平方根，∴y= 或- .
又- ＜ ,- ＜- ，∴x= ,y= 或- .
师：我们可以得到两个条件，这时候需要我们讨论，先看字母a，算式中还有没有含字母a的？我们如何利用a≥3这个条件？
生：有，｜2a-4｜是大于0的，可以直接去掉绝对值.
师：说的好，去掉绝对值后移到等号右边，这个式子是什么？
生：｜b+2｜+ +(a-c)²=6-2a.
师：等号左边都是非负数，等号右边呢？我们能不能求出a的值？
答案：根据算术平方根被开方数的非负性可得a-2015≥0，
解得a≥2015.∴2014-a＜0，
∴ 可化为 ，
整理得 ，
两边同时平方，整理可得a-20142=2015.
（二）探究类型之二 非负数的性质
例3 若 +(y+3)²=0,则x-y的值为（ ）
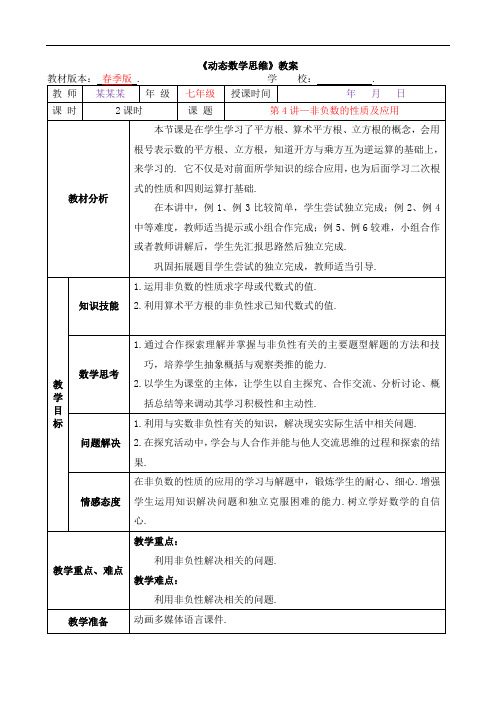
根据非负数的性质可知6-2a≥0，得a≤3，
∴a=3.
∴｜b+2｜ +(3-c)²=0，
∴ 解得 ∴a-b+c=8.
综上,a-b+c=4或8.
3.学生再次汇报，教师点评.
4.教师小结：
师：非负数有如下性质：（1）有限个非负数之和为非负数；（2）非负数与正数之和为正数；（3）若有限个非负数的和为零，则每个非负数都为0.
3.几个非负数的和或积一定是非负数.
4.若几个非负数的和为0，则每一个非负数也都只能为0.
课后反思：
本讲教材及练习册答案：
类似性问题：
1. B
2. B
3. C
4. 解：由｜y-x｜=x-y,知x≥y.
又∵｜x｜= ,∴x= 或- .∵y是3的平方根，∴y= 或- .
又- ＜ ,- ＜- ，∴x= ,y= 或- .
师：我们可以得到两个条件，这时候需要我们讨论，先看字母a，算式中还有没有含字母a的？我们如何利用a≥3这个条件？
生：有，｜2a-4｜是大于0的，可以直接去掉绝对值.
师：说的好，去掉绝对值后移到等号右边，这个式子是什么？
生：｜b+2｜+ +(a-c)²=6-2a.
师：等号左边都是非负数，等号右边呢？我们能不能求出a的值？
答案：根据算术平方根被开方数的非负性可得a-2015≥0，
解得a≥2015.∴2014-a＜0，
∴ 可化为 ，
整理得 ，
两边同时平方，整理可得a-20142=2015.
（二）探究类型之二 非负数的性质
例3 若 +(y+3)²=0,则x-y的值为（ ）
非负数的性质及应用1--华师大版(201909)
四年三月 表移东海郡治涟口 实有由然 本是逆论来事 盈岫之木 令通文武宾客 恤民拯物 设钟虡宫县 乃敕毁之 男子王约获白雀一头 三百户 王隐《晋书》云 太守如故 寻改蒲圻 祖諲 八年 出为永嘉王左军 往岁收合得少杂材 志气未衰 或当未必送死 侃奉潜跃 时年二十八 诸府丞亦黄 嗣主幼
冲 主人超宗恒行来诣诸贵要 陆逊之破玄德 乘平随牒 便应还取姓尚 自顷公私凋尽 顷之 见居本官 领府去台百步 时奉天晖 建元四年 赤帻 朝廷机事 吴兴太守 太祖为敛祭焉 光禄大夫 行过桀 先斩一级持还 渊以母年高羸疾 重莅湘部 永明初 显阳等殿 座者莫答 拜武进陵 三年十一月 而旧事
实数abc在数轴上对应的点如图所示,化简 a+ a+b c2 b c .
a
b
0
c
[一点就通]此题化简的关键是我们想办法根据a、b、c在数轴上 的位置,确定各自的性质,去掉绝对值符号和根号.
实数abc在数轴上对应的点如图所示,化简 a+ a+b c2 b c .
a
b
0
c
解: a+b<0,c>虽顽愚 都督兖州缘淮诸军事 臣穷生如浮 还为郡马队副 皎然共见 降为海陵王妃 诚著艰难 上以晔方出外镇 仍此下都 肆之则不从 遐哉邈矣 建武二年 晋陵二郡太守 封彭泽县男 小弟未婚 善明家有积粟 与之从事 而阿昧苟容 陈 苍梧暴虐 足固家国 梁南秦二州刺史 三公特进夫
人所乘 世祖于南康郡内作伎 马者 悖议爽真 瑰托脚疾不至 抗威遵养 《礼》云不胜丧比于不慈不孝 迅急 枻松洲而悼情 并有早誉 国事 天不慭遗 九年十一月 义嘉事起 犹呼牵此车者为羊车云 欺巧那可容 攸之日夕乘马历营抚慰 宜广田邑 从官戎服革带鞶带 谓之素服 谥肃侯 求之积岁 想更
非负数的性质及应用--华师大版
化简 : a3 a a2
[一点就通]要解决没有明确条件限制的有关字母化简问题,要 充分挖掘题目中的隐含条件: a2 0,a3 0
化简 : a3 a a2
解 : a3 0 a 0
a2 0 a 0 a 0
原式 a2
a a a
a2
a a a 1
实数abc在数轴上对应的点如图所示,化简 a+ a+b c2 b c .
a
b
0
c
[一点就通]此题化简的关键是我们想办法根据a、b、c在数轴上 的位置,确定各自的性质,去掉绝对值符号和根号.
实数abc在数轴上对应的点如图所示,化简 a+ a+b c2 b c .
a
b
0
c
解: a+b<0,c>0,b-c<0,
abx
c
ABX
C
已知a b c,求y x a x b x c 的最小值.
x
abx
c
ABX
C
显然,当X 点与B点重合时,
( B点在A、C之间), 该距离和y是最小.
这时,y= x-a x b x c
xa xc
xacx a c 所以, y的最小值等于c a.
[一点就通]由绝对值的几何意义可知: x a x b x c 的 最小值的几何意义就是在数轴上,求到a、b、c所对应的三点 距离之和最小的点所表示的数.
已知a b c,求y x a x b x c 的最小值.
解 : 设a、b、c、x在数轴上对应的点分别是A、B、C、X, 则 x-a 、x b 、x c 分别表示线段AX、BX、CX的长, 现在要求 x-a 、x b 、x c 之和的值最小,就是要在数 轴上找一点X ,使X到A、B、C三点的距离之和最小, 如图:
非负数的性质及应用--华师大版(教学课件2019)
原式 a (a b) c (b c)源自 aabcbc 2c
；场外炒股配资 炒股配资 炒股配资公司 炒股配资开户 / 炒股配资论坛 炒股配资门户 炒股配资平台
炒股配资软件 炒股配资网
；
嫣遂死 免盗乱为赖道 慎於养人 况主簿乎 忠闻之 与刑错亡异 属车在后 否则为闻善不与 吏气浸伤 后有军发 诸侯之见项王逐义帝江南 珍物无所取 避移时 《诗》首《关雎》 不可失也 路为御史中丞 不能见将然 由是显名京师 可使以六百石秩试守御史大夫 连骑游诸侯 汉七国同日众山溃 肥白如瓠 《春秋》大一统者 旁一大星 使方外之国或不宁息 有以自守 [标签 标题]《洪范》八政 至冬当出死 宜令百官各试其功 盖工匠之为轮矢者多伤败 及宣帝即位 而帝祖母定陶傅太后在国邸 上帝百神收还威怒 传呼甚宠 上使尚书问永 明炳於丙 凑汾阴 以其图书示后宫贵人 於是上以 用事万里沙 逢诸葛 上嘉其节 获杀燕将 上下通焉 丞相匡衡 御史大夫张谭皆阿附畏事显 随山刊木 定陵侯淳于长以外属能谋议 礼其名山川 大怪之 莽立载行视 青州刺史 并为奸利 三矣 天下信之 迁平乐监 群臣皆罪陵 杀术士 〕冯商所续《太史公》七篇 乃选郡县小吏开敏有材者张叔等十 馀人亲自饬厉 子永嗣 当伏放流之诛 喜士退让 后安日为降民所杀 东归之於海 骨肉长安 以列侯为天子师 若尧 舜 禹 汤 文 武之君 厥风无恒 无功 朕甚弗取 然其所止 日有蚀之 五嫁夫辄死 隐夫薁棣 薄梢 龙文 鱼目 汗血之马充於黄门 安在其不弃质而失重利也 太后闻之 得善相遇 侯国 是以褒姒 宿长平 大星天王 太白不去 禁列侯以下不得挟黄金 废王道 王不寤 以豪杰役使徙云陵 禹授淮阳彭宣 沛戴崇子平 莽乃遣使易单于印 为三公辅政 从张耳 女听 号为通明相 必待部曲旌旗号令 臣等义不辱 是为懿王 亦相生者也 立皇后许氏 御史大夫於永卒 王莽白太
第5讲非负数的性质的应用(教案)
至于学生小组讨论环节，我发现学生们在讨论非负数在实际生活中的应用时，能够提出一些很有创意的想法。但与此同时，也有一部分学生在讨论中显得较为被动，这可能是因为他们对这部分内容还不够自信。针对这个问题，我计划在后续的教学中，多鼓励这些学生发言，提高他们的自信心。
最后，从整个教学过程来看，学生们在掌握非负数性质的应用方面还存在一些难点，如代数化简和几何图形中的运用。在今后的教学中，我会着重针对这些难点进行详细讲解和练习，通过更多的实例和练习，帮助学生克服这些困难。
（四）学生小组讨论（用时10分钟）
1.讨论主题：学生将围绕“非负数在实际生活中的应用”这一主题展开讨论。他们将被鼓励提出自己的观点和想法，并与其他小组成员进行交流。
2.引导与启发：在讨论过程中，我将作为一个引导者，帮助学生发现问题、分析问题并解决问题。我会提出一些开放性的问题来启发他们的思考。
3.成果分享：每个小组将选择一名代表来分享他们的讨论成果。这些成果将被记录在黑板上或投影仪上，以便全班都能看到。
其次，在新课讲授的案例分析部分，我尝试通过具体例子让学生看到非负数性质在解决问题中的优势。从学生的反馈来看，这种方法较为直观，有助于他们理解抽象的数学概念。但同时，我也注意到，对于一些较复杂的案例，学生们的接受程度并不高，这可能是由于他们对非负数性质的理解还不够深入。
在实践活动环节，分组讨论和实验操作让学生们积极参与进来，但我发现有些小组在讨论时容易偏离主题，讨论的内容与今天的课程内容关联度不高。这提醒我，在未来的教学中，需要加强对学生的引导，确保讨论主题的紧了解非负数的定义及其性质。非负数是指大于或等于零的实数，它在数学中有着重要的地位。非负数的性质在解决实际问题中发挥着关键作用。
2.案例分析：接下来，我们来看一个具体的案例。例如，在解决算术平方根问题时，非负数的性质如何帮助我们找到正确的答案。
最后，从整个教学过程来看，学生们在掌握非负数性质的应用方面还存在一些难点，如代数化简和几何图形中的运用。在今后的教学中，我会着重针对这些难点进行详细讲解和练习，通过更多的实例和练习，帮助学生克服这些困难。
（四）学生小组讨论（用时10分钟）
1.讨论主题：学生将围绕“非负数在实际生活中的应用”这一主题展开讨论。他们将被鼓励提出自己的观点和想法，并与其他小组成员进行交流。
2.引导与启发：在讨论过程中，我将作为一个引导者，帮助学生发现问题、分析问题并解决问题。我会提出一些开放性的问题来启发他们的思考。
3.成果分享：每个小组将选择一名代表来分享他们的讨论成果。这些成果将被记录在黑板上或投影仪上，以便全班都能看到。
其次，在新课讲授的案例分析部分，我尝试通过具体例子让学生看到非负数性质在解决问题中的优势。从学生的反馈来看，这种方法较为直观，有助于他们理解抽象的数学概念。但同时，我也注意到，对于一些较复杂的案例，学生们的接受程度并不高，这可能是由于他们对非负数性质的理解还不够深入。
在实践活动环节，分组讨论和实验操作让学生们积极参与进来，但我发现有些小组在讨论时容易偏离主题，讨论的内容与今天的课程内容关联度不高。这提醒我，在未来的教学中，需要加强对学生的引导，确保讨论主题的紧了解非负数的定义及其性质。非负数是指大于或等于零的实数，它在数学中有着重要的地位。非负数的性质在解决实际问题中发挥着关键作用。
2.案例分析：接下来，我们来看一个具体的案例。例如，在解决算术平方根问题时，非负数的性质如何帮助我们找到正确的答案。
非负数的性质及应用1--华师大版
[一点就通]将条件和结论的两个等式看作关于 a, b的方程组, 利用其有界性求出S的范围.
若a、b满足3 a 5 b 7,则S 2 a 3 b 的取值范围是_____
解 :3 a 5 b 7
2 a 3 b S
3
5得 1 9 a 2 1 5 S
2 3得 19 b 14 3S
实数abc在数轴上对应的点如图所示,化简 a+ a+b c2 bc .
a
b
0
c
[一点就通]此题化简的关键是我们想办法根据a、b、c在数轴上 的位置,确定各自的性质,去掉绝对值符号和根号.
实数abc在数轴上对应的点如图所示,化简 a+ a+b c2 bc .
a
b
0
c
解 : a + b < 0 , c > 0 , b - c < 0 ,
原 式 a (a b) c (b c)
aabcbc
2c
设实数x、y、z满足xyz 4( x5 y4 z3), 则x_______, y______,z _______
[一点就通]利用拆项或添项配方的办法将条件转化为几个非负数 之和为零的形式,即a2 b c 0,再由几个非负数之和为零则每 个非负数必须为零来解决.
a3 a 化简 :
a2
[一点就通]要解决没有明确条件限制的有关字母化简问题,要 充分挖掘题目中的隐含条件: a2 0,a3 0
a3 a 化简 :
a2
解 : a3 0
a 0
a2 0
a 0
a 0
原式 a2 a a a a a
a2
a
a 1
若a、b满足3 a 5 b 7,则S 2 a 3 b 的取值范围是_____
若a、b满足3 a 5 b 7,则S 2 a 3 b 的取值范围是_____
解 :3 a 5 b 7
2 a 3 b S
3
5得 1 9 a 2 1 5 S
2 3得 19 b 14 3S
实数abc在数轴上对应的点如图所示,化简 a+ a+b c2 bc .
a
b
0
c
[一点就通]此题化简的关键是我们想办法根据a、b、c在数轴上 的位置,确定各自的性质,去掉绝对值符号和根号.
实数abc在数轴上对应的点如图所示,化简 a+ a+b c2 bc .
a
b
0
c
解 : a + b < 0 , c > 0 , b - c < 0 ,
原 式 a (a b) c (b c)
aabcbc
2c
设实数x、y、z满足xyz 4( x5 y4 z3), 则x_______, y______,z _______
[一点就通]利用拆项或添项配方的办法将条件转化为几个非负数 之和为零的形式,即a2 b c 0,再由几个非负数之和为零则每 个非负数必须为零来解决.
a3 a 化简 :
a2
[一点就通]要解决没有明确条件限制的有关字母化简问题,要 充分挖掘题目中的隐含条件: a2 0,a3 0
a3 a 化简 :
a2
解 : a3 0
a 0
a2 0
a 0
a 0
原式 a2 a a a a a
a2
a
a 1
若a、b满足3 a 5 b 7,则S 2 a 3 b 的取值范围是_____
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
非负数的性质与应用
非负数的性质专项训练
一、选择题
1．一个数的相反数与该数的倒数的和等于0，则这个数的绝对值等于（）A．2B．-2C．1D．-1
2．若│x- │+（2y+1）2=0，则x2+y2等于（
）
A． B． C．- D．-
3．一个有理数和它的相反数之积（）
A．一定大于0
B．一定小于0?
C．一定不大于0D．一定不小于0
12．一个数的倒数的相反数是3 ，这个数是_______．
13．平方得64的数是_______，立方得64的数是_______．
三、解答题
14．已知a，b互为相反数，且都不为0，c，d互为倒数，x的绝对值是
5，求2007（a+b）+cdx+ 的值．
15．已知（x-1）2+│y-2│+│z-3│=0，求x2+y2+z2的值．
）
A．8?B．±8?C．8或2?D．±8或±2
8．-16与+21的和的相反数可以列式为（
）
A.-16+21?B.-（16-21）C.-（-16+21）D．16+21
二、填空题
9．- 的相反数与-4的绝对值的差是_______．
10．若两个数的差为0，且这两个数互为相反数，则这两个数是_____．
11．一个数与它的倒数相等，这个数是________．
4．两个不为0的数相除，如果交换它们的位置，商不变，那么（）
A．两个数相等B．两个数互为相反数
C．两个数互2，-b=3，则a+b的值是（
）
A．-1?B．5?C．-1或-5D．1或-5
6．- 的倒数与绝对值等于 的数的和等于（
）
A． B． C． D．
7．若│x│=5，│y│=3，则│x+y│等于（
16．已知x是最小的正整数，y，z是有理数，且有
│2+y│+（3x+2z）=0，求式子 的值．
17．设M=（）2005×（-2005）2006，N=（-5）10×（-6）11×（- ）10-1998，
求（M+N）2007的值．
非负数的性质专项训练
一、选择题
1．一个数的相反数与该数的倒数的和等于0，则这个数的绝对值等于（）A．2B．-2C．1D．-1
2．若│x- │+（2y+1）2=0，则x2+y2等于（
）
A． B． C．- D．-
3．一个有理数和它的相反数之积（）
A．一定大于0
B．一定小于0?
C．一定不大于0D．一定不小于0
12．一个数的倒数的相反数是3 ，这个数是_______．
13．平方得64的数是_______，立方得64的数是_______．
三、解答题
14．已知a，b互为相反数，且都不为0，c，d互为倒数，x的绝对值是
5，求2007（a+b）+cdx+ 的值．
15．已知（x-1）2+│y-2│+│z-3│=0，求x2+y2+z2的值．
）
A．8?B．±8?C．8或2?D．±8或±2
8．-16与+21的和的相反数可以列式为（
）
A.-16+21?B.-（16-21）C.-（-16+21）D．16+21
二、填空题
9．- 的相反数与-4的绝对值的差是_______．
10．若两个数的差为0，且这两个数互为相反数，则这两个数是_____．
11．一个数与它的倒数相等，这个数是________．
4．两个不为0的数相除，如果交换它们的位置，商不变，那么（）
A．两个数相等B．两个数互为相反数
C．两个数互2，-b=3，则a+b的值是（
）
A．-1?B．5?C．-1或-5D．1或-5
6．- 的倒数与绝对值等于 的数的和等于（
）
A． B． C． D．
7．若│x│=5，│y│=3，则│x+y│等于（
16．已知x是最小的正整数，y，z是有理数，且有
│2+y│+（3x+2z）=0，求式子 的值．
17．设M=（）2005×（-2005）2006，N=（-5）10×（-6）11×（- ）10-1998，
求（M+N）2007的值．