山东省济南市2019届高三上学期期末考试数学(文)试卷+Word版含解析
山东省济南市2019-2020学年高三上学期期末数学试题

高三年级学习质量评估数学试题 参考公式:锥体的体积公式:13V Sh =(其中S 为锥体的底面积,h 为锥体的高) 一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合2{|60}A x x x =--≤,{|10}B x x =-<,则AB =( ) A. (,3]-∞ B. (,2]-∞ C. (,1)-∞ D. [2,1)-2.若复数z 满足(1)2z i i +=-(其中i 为虚数单位),则z 的共轭复数是( ) A. 1i - B. 1i + C. 1i -- D. 1i -+ 3.设x ∈R ,则“24x >”是“lg(||1)0x ->”的( )A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件4.已知函数ln ,0(),0e x x x x f x x x >⎧⎪=⎨≤⎪⎩则函数()1y f x =-的图象大致是( ) A. B.C. D.5.若抛物线22y px =(0)p >焦点到准线的距离为2,过焦点的直线与抛物线交于A ,B 两点,且8AB =,则弦AB 的中点到y 轴的距离为( )A. 2B. 3C. 4D. 6 6.已知函数21()lg(1)2f x x x =+++,则1(ln 5)ln 5f f ⎛⎫+= ⎪⎝⎭( ) A. 0 B. 12C. 1D. 2 7.考古发现,在埃及金字塔内有一组神秘的数字142857,因为1428572285714⨯=,1428573428571⨯=,…所以这组数字又叫走马灯数.该组数字还有如下规律:142857999+=,571428999+=,…若从1,4,2,8,5,7这6个数字中任意取出3个数字构成一个三位数x ,则999x -的结果恰好是剩下3个数字构成的一个三位数的概率为( )A. 45B. 35C. 25D. 3108.若F 为双曲线22:145x y C 的左焦点,过原点的直线l 与双曲线C 的左右两支分别交于A ,B 两点,则14||||FA FB -的取值范围是( ) A. 11,45⎡⎤⎢⎥⎣⎦ B. 11,55⎡⎤-⎢⎥⎣⎦C. 1,04⎛⎤- ⎥⎝⎦D. 11,45⎡⎤-⎢⎥⎣⎦二、多项选择题本题:共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分.9.习总书记讲到:“广大人民群众坚持爱国奉献,无怨无悔,让我感到千千万万普通人最伟大,同时让我感到幸福都是奋斗出来的”.某企业2019年12个月的收入与支出数据的折线图如下:已知:利润=收入-支出,根据该折线图,下列说法正确的是( )A. 该企业2019年1月至6月的总利润低于2019年7月至12月的总利润B. 该企业2019年第一季度的利润约是60万元C. 该企业2019年4月至7月的月利润持续增长D. 该企业2019年11月份的月利润最大10.声音是由物体振动产生的声波,其中包含着正弦函数.纯音的数学模型是函数sin y A t ω=,我们听到的声音是由纯音合成的,称之为复合音.若一个复合音的数学模型是函数()1sin sin 22f x x x =+,则下列结论正确的是( )A. 2π是()f x 的一个周期B. ()f x 在0,2π上有3个零点C. ()f x 的最大值为334 D. ()f x 在0,2π⎡⎤⎢⎥⎣⎦上是增函数 11.给定两个不共线的空间向量a 与b ,定义叉乘运算:a b ⨯.规定:①a b ⨯为同时与a ,b 垂直的向量;②a ,b ,a b ⨯三个向量构成右手系(如图1);③sin ,a b a b a b ⨯=.如图2,在长方体1111ABCD A B C D -中,2AB AD ==,14AA =,则下列结论正确的是( )A. 1AB AD AA ⨯=B. AB AD AD AB ⨯=⨯C. 111()AB AD AA AB AA AD AA +⨯=⨯+⨯D. 长方体1111ABCD A B C D -的体积1()V AB AD CC =⨯⋅。
2019-2020学年山东省济南市高三(上)期末数学试卷(含解析)

2019-2020学年山东省济南市高三(上)期末数学试卷一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合A ={x|x 2−x −6≤0},B ={x|x −1<0},则A ∪B =( ) A.(−∞, 3]B.(−∞, 2]C.(−∞, 1)D.[−2, 1)2.若复数z 满足z(1+i)=−2i (其中i 为虚数单位),则z 的共轭复数是( ) A.1−iB.1+iC.−1−iD.−1+i3.设x ∈R ,则“2x >4”是“lg(|x|−1)>0”的( ) A.充分不必要条件 B.必要不充分条件 C.充要条件D.既不充分也不必要条件4.已知函数f(x)={xlnx,x >0x e,x ≤0 则函数y =f(1−x)的图象大致是( )A. B. C. D.5.若抛物线y 2=2px(p >0)的焦点到准线的距离为2,过焦点的直线与抛物线交于A ,B 两点,且|AB|=8,则弦AB 的中点到y 轴的距离为( ) A.2B.3C.4D.66.已知函数f(x)=lg(√x 2+1+x)+12,则f(ln5)+f(ln 15)=() A.0B.12C.1D.27.考古发现,在埃及金字塔内有一组神秘的数字142857,因为142857×2=285714,142857×3=428571,…所以这组数字又叫走马灯数.该组数字还有如下规律:142+857=999,571+428=999,…若从1,4,2,8,5,7这6个数字中任意取出3个数字构成一个三位数x ,则999−x 的结果恰好是剩下3个数字构成的一个三位数的概率为( ) A.45B.35C.25D.3108.若F 为双曲线C:x 24−y 25=1的左焦点,过原点的直线l 与双曲线C 的左右两支分别交于A ,B 两点,则1|FA|−4|FB|的取值范围是( )A.[14,15]B.[−15,15]C.(−14,0]D.[−14,15]二、多项选择题本题:共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分.9.习总书记讲到:“广大人民群众坚持爱国奉献,无怨无悔,让我感到千千万万普通人最伟大,同时让我感到幸福都是奋斗出来的”.某企业2019年12个月的收入与支出数据的折线图如下:已知:利润=收入-支出,根据该折线图,下列说法正确的是( ) A.该企业2019年1月至6月的总利润低于2019年7月至12月的总利润 B.该企业2019年第一季度的利润约是60万元 C.该企业2019年4月至7月的月利润持续增长 D.该企业2019年11月份的月利润最大10.声音是由物体振动产生的声波,其中包含着正弦函数.纯音的数学模型是函数y =Asinωt ,我们听到的声音是由纯音合成的,称之为复合音.若一个复合音的数学模型是函数f(x)=sinx +12sin2x ,则下列结论正确的是( ) A.2π是f(x)的一个周期 B.f(x)在[0, 2π]上有3个零点 C.f(x)的最大值为3√34D.f(x)在[0,π2]上是增函数11.给定两个不共线的空间向量a →与b →,定义叉乘运算:a →×b →.规定:①a →×b →为同时与a →,b →垂直的向量;②a →,b →,a →×b →三个向量构成右手系(如图1);③|a →×b →|=|a →||b →|sin <a →,b →>.如图2,在长方体ABCD −A 1B 1C 1D 1中,AB =AD =2,AA 1=4,则下列结论正确的是( ) A.AB →×AD →=AA 1→B.AB →×AD →=AD →×AB →C.(AB →+AD →)×AA 1→=AB →×AA 1→+AD →×AA 1→D.长方体ABCD −A 1B 1C 1D 1的体积V =(AB →×AD →)⋅CC 1→12.若实数a ,b 满足2a +3a =3b +2b ,则下列关系式中可能成立的是( ) A.0<a <b <1 B.b <a <0C.1<a <bD.a =b三、填空题:本题共4小题,每小题5分,共20分.13.(2x −y)5的展开式中,含x 3y 2项的系数为________.(用数字作答). 14.已知sin(α−π3)=−3cos(α−π6),则tan2α=________15.平行四边形ABCD 中,M 为CD 的中点,点N 满足BN →=2NC →,若AB →=λAM →+μAN →,则λ+μ的值为________.16.如图,矩形ABCD 中,AB =2√3,AD =2,Q 为BC 的中点,点M ,N 分别在线段AB ,CD 上运动(其中M 不与A ,B 重合,N 不与C ,D 重合),且MN // AD ,沿MN 将△DMN 折起,得到三棱锥D −MNQ ,则三棱锥D −MNQ 体积的最大值为________;当三棱锥D −MNQ 体积最大时,其外接球的表面积的值为________.四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.在①b 2+√2ac =a 2+c 2,②acosB =bsinA ,③sinB +cosB =√2这三个条件中任选一个,补充在下面的问题中,并解决该问题.已知△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,A =π3,b =√2,求△ABC 的面积.18.如图,五面体ABCDEF 中,正方形ABCD 的边长为2√2,AB =2EF ,EF // 平面ABCD ,点P 在线段DE 上,且DP =2PE ,Q 为BC 的中点.(1)求证:BE // 平面APQ ;(2)已知AE ⊥平面ABCD ,且AE =2,求二面角P −AF −E 的余弦值.19.数学家也有一些美丽的错误,如法国数学家费马于1640年提出了以下猜想:F n =22n+1(n ∈N)是质数.1732年,瑞士数学家欧拉算出F 5=641×6700417,该数不是质数.已知S n 为数列{a n }的前n 项和,且S n =log 2(F n −1)−1(n ∈N +) (1)求数列{a n }的通项公式;(2)若b n =(n +1)log 2a n+1,设为数列{2b n}的前n 项和,求出T n ,并证明:对任意n ∈N +,1≤T n <2.20.截止到2018年末,我国公路总里程达到484.65万公里,其中高速公路达到14.26万公里,规模居世界第一.与此同时,行车安全问题也成为管理部门关注的重点.如图是某部门公布的一年内道路交通事故成因分析,由图可知,超速驾驶已经成为交通事故的一个主要因素.研究表明,急刹车时的停车距离等于反应距离与制动距离的和,下表是根据某部门的调查结果整理所得的数据(v 表示行车速度,单位:km/ℎ;d 1,d 2分别表示反应距离和制动距离,单位:m) 道路交通事故成因分析 v 64 72 80 89 97 105 113 121 128 135 d 113.415.216.718.620.121.923.525.326.828.5(1)从一年内发生的道路交通事故中随机抽出3起进行分析研究,求其中恰好有1起属于超速驾驶的概率(用频率代替概率);(2)已知d 2与v 的平方成正比,且当行车速度为100km/ℎ时,制动距离为65m .(i)由表中数据可知,d 1与v 之间具有线性相关关系,请建立d 1与v 之间的回归方程,并估计车速为110km/ℎ时的停车距离;(ii)我国《道路交通安全法》规定:车速超过100km/ℎ时,应该与同车道前车保持100m 以上的距离,请解释一下上述规定的合理性.参考数据:∑=i=110 vi 1004,∑=i=110 (d1)i 210,∑(i=110 vi d 1)i =22187.3,∑=i=110 vi 2106054,1103352524≈0.21参考公式:对于一组数据(x 1, y 1),(x 2, y 2),…,(x n , y n ),其回归直线y =b x +a 的斜率和截距的最小二乘估计分别为:b =∑ n i=1(x i −x ¯)(y i −y ¯)∑ n i=1(x i −x ¯)2,a =y ¯−b x ¯.21.已知F1,F2分别为椭圆C:x 2a2+y2b2=1(a>b>0)的左、右焦点,P为C上的动点,其中P到F1的最短距离为1,且当△PF1F2的面积最大时,△PF1F2恰好为等边三角形.(1)求椭圆C的标准方程;(2)以椭圆长轴为直径的圆叫做椭圆的“外切圆”,记椭圆C的外切圆为E.(i)求圆E的方程;(ii)在平面内是否存在定点Q,使得以PQ为直径的圆与E相切,若存在求出定点Q的坐标;若不存在,请说明理由22.已知函数f(x)=lnxx +k的极大值为1+ee,其中e=2.71828…为自然对数的底数.(1)求实数k的值;(2)若函数g(x)=e x−ax,对任意x∈(0, +∞),g(x)≥af(x)恒成立.(i)求实数a的取值范围;(ii)证明:x2f(x)>asinx+x2−1.2019-2020学年山东省济南市高三(上)期末数学试卷一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合A ={x|x 2−x −6≤0},B ={x|x −1<0},则A ∪B =( ) A.(−∞, 3] B.(−∞, 2] C.(−∞, 1) D.[−2, 1)【解答】∵集合A ={x|x 2−x −6≤0}={x|−2≤x ≤3}, B ={x|x −1<0}={x|x <1}, ∴A ∪B ={x|x ≤3}=(−∞, 3].2.若复数z 满足z(1+i)=−2i (其中i 为虚数单位),则z 的共轭复数是( ) A.1−i B.1+i C.−1−i D.−1+i【解答】∵z(1+i)=−2i ,∴z =−2i1+i =−2i(1−i)(1+i)(1−i)=−1−i , 则z ¯=−1+i .3.设x ∈R ,则“2x >4”是“lg(|x|−1)>0”的( ) A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件【解答】设x ∈R ,则“2x >4”⇒“lg(|x|−1)>0”,“lg(|x|−1)>0”⇒“x >2或x <−2”⇒“2x >4或2x <14”, ∴“2x >4”是“lg(|x|−1)>0”的充分不必要条件.4.已知函数f(x)={xlnx,x >0x ex ,x ≤0 则函数y =f(1−x)的图象大致是( )A. B.C. D.【解答】当x >0时,f(x)=xlnx ,则令f′(x)=lnx +1=0,解得x =1e ,所以当0<x <1e 时,f(x)单调递减,x >1e 时,f(x)单调递增,当x ≤0时,f(x)=xe x ,则令f′(x)=e −x −1≥0,所以当x ≤0时,f(x)单调递增, 作出函数f(x)的图象如图:又因为f(1−x)的图象时将f(x)图象先关于y 轴对称,再向左移动一个单位得到的, 故根据f(x)图象可值f(1−x)图象为5.若抛物线y 2=2px(p >0)的焦点到准线的距离为2,过焦点的直线与抛物线交于A ,B 两点,且|AB|=8,则弦AB 的中点到y 轴的距离为( ) A.2 B.3 C.4 D.6【解答】抛物线y 2=2px(p >0)的焦点到准线的距离为2,可得p =2,抛物线方程为:y 2=4x , 设A(x 1, y 1),B(x 2, y 2),根据抛物线定义,x 1+x 2+p =8, 所以x 1+x 2=6,∵AB 的中点的横坐标为:3,中点到y 轴的距离为3,6.已知函数f(x)=lg(√x 2+1+x)+12,则f(ln5)+f(ln 15)=() A.0 B.12C.1D.2【解答】根据题意,函数f(x)=lg(√x 2+1+x)+12,则f(−x)=lg(√x 2+1−x)+12=−lg(√x 2+1−x)+12,则f(x)+f(−x)=1,则有f(ln5)+f(ln 15)=f(ln5)+f(−ln5)=1;7.考古发现,在埃及金字塔内有一组神秘的数字142857,因为142857×2=285714,142857×3=428571,…所以这组数字又叫走马灯数.该组数字还有如下规律:142+857=999,571+428=999,…若从1,4,2,8,5,7这6个数字中任意取出3个数字构成一个三位数x ,则999−x 的结果恰好是剩下3个数字构成的一个三位数的概率为( )A.45 B.35C.25D.310【解答】根据题意,从1,4,2,8,5,7这6个数字中任意取出3个数字构成一个三位数x ,共有A3#/DEL/#6#/DEL/#=6×5×4=120种.又因为从1,4,2,8,5,7这6个数字中:1+8=9,2+7=9,4+5=9,共3组.所以要使6个数字中任意取出3个数字构成一个三位数x ,999−x 的结果恰好是剩下3个数字构成的一个三位数,则每次抽取只能抽取一组数字中的一个, 所以共有∁61∁41∁21=6×4×2=48种, 故P =48120=25. 8.若F 为双曲线C:x 24−y 25=1的左焦点,过原点的直线l 与双曲线C 的左右两支分别交于A ,B 两点,则1|FA|−4|FB|的取值范围是( ) A.[14,15] B.[−15,15]C.(−14,0]D.[−14,15]【解答】 双曲线C:x 24−y 25=1的a =2,b =√5,c =3,设|AF|=m ,|FB|=n ,F ′为双曲线的右焦点,连接BF ′,AF ′,由对称性可得四边形AFBF ′为平行四边形,可得|BF ′|=|AF|=m ,可得n −m =2a =4,n =m +4, 且m ≥c −a =1,则1|FA|−4|FB|=1m −44+m ,设f(m)=1m −44+m ,m ≥1, f′(m)=−1m 2+4(4+m)2=(m−4)(3m+4)m 2(4+m)2,当m >4时,f′(m)>0,f(m)递增,1≤m <4时,f′(m)<0,f(m)递减, 可得f(m)在m =4处取得极小值,且为最小值−14, 当m =1时,f(1)=15,当m →+∞时,f(m)→0, 则f(m)∈[−14, 15], 故选:D .二、多项选择题本题:共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分.9.习总书记讲到:“广大人民群众坚持爱国奉献,无怨无悔,让我感到千千万万普通人最伟大,同时让我感到幸福都是奋斗出来的”.某企业2019年12个月的收入与支出数据的折线图如下:已知:利润=收入-支出,根据该折线图,下列说法正确的是()A.该企业2019年1月至6月的总利润低于2019年7月至12月的总利润B.该企业2019年第一季度的利润约是60万元C.该企业2019年4月至7月的月利润持续增长D.该企业2019年11月份的月利润最大【解答】由企业2019年12个月的收入与支出数据的折线图,得:在A中,该企业2019年1月至6月的总利润约为:x1=(30+40+35+30+50+60)−(20+25+10+20+22+30)=118,该企业2019年7月至12月的总利润约为:(80+75+75+80+90+80)−(28+22+30+40+45+50)=265,∴该企业2019年1月至6月的总利润低于2019年7月至12月的总利润,故A正确;在B中,该企业2019年第一季度的利润约约是:(30+40+35)−(20+25+10)=50万元,故B错误;在C中,该企业2019年4月至7月的月利润分别为(单位:万元):10,28,30,52,∴该企业2019年4月至7月的月利润持续增长,故C正确;在D中,该企业2019年7月和8月的月利润比11月份的月利润大,故D错误.10.声音是由物体振动产生的声波,其中包含着正弦函数.纯音的数学模型是函数y=Asinωt,我们sin2x,听到的声音是由纯音合成的,称之为复合音.若一个复合音的数学模型是函数f(x)=sinx+12则下列结论正确的是()A.2π是f(x)的一个周期B.f(x)在[0, 2π]上有3个零点C.f(x)的最大值为3√34D.f(x)在[0,π2]上是增函数【解答】∵y =sinx 的周期为2π,y =12sin2x 的周期为π,∴f(x)=sinx +12sin2x 的周期为2π,故A 正确; 由f(x)=sinx +12sin2x =0,得sinx +sinxcosx =0,得sinx =0或cosx =−1, ∵x ∈[0, 2π],∴x =0,x =π,x =2π,则f(x)在[0, 2π]上有3个零点,故B 正确; 函数f(x)=sinx +12sin2x 的最大值在[0, π2]上取得,由f′(x)=cosx +cos2x =2cos 2x +cosx −1=0,可得cosx =12,当x ∈(0, π3)时,cosx 单调递减,原函数单调递增,当x ∈(π3, π2)时,cosx 单调递减,原函数单调递减,则当x =π3时,原函数求得最大值为sin π3+12sin 2π3=3√34,故C 正确; ∵f(π4)=sin π4+12sin π2=√2+12>1,f(π2)=sin π2+12sinπ=1,∴f(x)在[0,π2]上不是增函数,故D 错误.11.给定两个不共线的空间向量a →与b →,定义叉乘运算:a →×b →.规定:①a →×b →为同时与a →,b →垂直的向量;②a →,b →,a →×b →三个向量构成右手系(如图1);③|a →×b →|=|a →||b →|sin <a →,b →>.如图2,在长方体ABCD −A 1B 1C 1D 1中,AB =AD =2,AA 1=4,则下列结论正确的是( )A.AB →×AD →=AA 1→B.AB →×AD →=AD →×AB →C.(AB →+AD →)×AA 1→=AB →×AA 1→+AD →×AA 1→D.长方体ABCD −A 1B 1C 1D 1的体积V =(AB →×AD →)⋅CC 1→【解答】∵|AB →×AD →|=|AB →||AD →|sin90=2×2×1=4,且AA 1→分别与AB →AD →垂直,∴AB →×AD →=AA 1→,故A 正确;由题意,AB →×AD →=AA 1→,AD →×AB →=A 1A →,故B 错误;∵AB →+AD →=AC →,∴|(AB →+AD →)×AA 1→|=|AC →×AA 1→|=2√2×4×1=8√2,且(AB →+AD →)×AA 1→与DB →共线同向,∵|AB →×AA 1→|=2×4×1=8,AB →×AA 1→与DA →共线同向,|AD →×AA 1→|=2×4×1=8,AD →×AA 1→与DB →共线同向,∴|AB →×AA 1→+AD →×AA 1→|=8√2,且AB →×AA 1→+AD →×AA 1→与DB →共线同向,故C 正确; (AB →×AD →)⋅CC 1→=|AB →||AD →|×|CC 1→|×sin90×cos0=2×2×4=16,故D 成立. 12.若实数a ,b 满足2a +3a =3b +2b ,则下列关系式中可能成立的是() A.0<a <b <1 B.b <a <0 C.1<a <bD.a =b【解答】解:由2a +3a =3b +2b ,设f(x)=2x +3x ,g(x)=3x +2x ,易知f(x),g(x)是单调递增函数, 画出f(x),g(x)的图象如图:根据图象可知:当x =0,1时,f(x)=g(x), 0<a <b <1,f(a)=g(b)可能成立,故A 正确;当b <a <0时,因为f(x)≤g(x),所以f(a)=g(b)可能成立,B 正确; 当a =b 时,显然成立,故D 正确;当1<a <b 时,因为f(a)<g(b),所以不可能成立,故C 错误. 故选ABD .三、填空题:本题共4小题,每小题5分,共20分.13.(2x −y)5的展开式中,含x 3y 2项的系数为________.(用数字作答). 【解答】二项式(2x −y)5的展开式的通项为T r+1=25−r (−1)r C 5r x 5−r y r , 令r =2,可得含x 3y 2的项的系数是23C 52=8014.已知sin(α−π3)=−3cos(α−π6),则tan2α=________ 【解答】由于sin(α−π3)=−3cos(α−π6),所以:12sinα−√32cosα=−3√32cosα−32sinα,整理得:√3cosα=−2sinα, 所以:tanα=−√32, 则:tan2α=2tanα1−tan 2α=−4√3,15.平行四边形ABCD 中,M 为CD 的中点,点N 满足BN →=2NC →,若AB →=λAM →+μAN →,则λ+μ的值为________. 【解答】平行四边形ABCD 中,M 为CD 的中点,点N 满足BN →=2NC →, 所以AB →=λAM →+μAN →=λ(AD →+12AB →)+μ(AB →+23AD →), =(λ+23μ)AD →+(12λ+μ)AB →,则根据平面向量基本定理可得,{λ+2μ3=01=12λ+μ ,解可得,λ=−1,μ=32, 则λ+μ=12,16.如图,矩形ABCD 中,AB =2√3,AD =2,Q 为BC 的中点,点M ,N 分别在线段AB ,CD 上运动(其中M 不与A ,B 重合,N 不与C ,D 重合),且MN // AD ,沿MN 将△DMN 折起,得到三棱锥D −MNQ ,则三棱锥D −MNQ 体积的最大值为________;当三棱锥D −MNQ 体积最大时,其外接球的表面积的值为________.【解答】设MB =t ,则AM =DN =2√3−t ,∵沿MN 将△DMN 折起,当DN ⊥平面MNQ 时,三棱锥D −MNQ 的体积最大, 此时V D−MNQ =13×12×MN ×MB ×t =13t(2√3−t)=−13t 2+2√33t , ∴当t =√3时,V D−MNQ 取最大值,最大值为1,此时MB =√3,DN =√3,∴MQ =NQ =2,∴△MNQ 为等边三角形,∴当三棱锥D −MNQ 体积最大时,三棱锥D −MNQ 是正三棱柱的一部分,如图所示:则三棱柱MNQ−EDF的外接球即是三棱锥D−MNQ的外接球,设点G,H分别是上下地面正三角形的中心,∴线段GH的中点即是三棱柱MNQ−EDF的外接球的球心O,∴OH=12DN=√32又,∴△MNQ是边长为2的等边三角形,∴HQ=2√33,∴三棱柱MNQ−EDF的外接球的半径R=OQ=√OH2+HQ2=5√36,∴三棱锥D−MNQ的外接球的表面积为4πR2=25π3,故答案为:1;25π3.四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.在①b2+√2ac=a2+c2,②acosB=bsinA,③sinB+cosB=√2这三个条件中任选一个,补充在下面的问题中,并解决该问题.已知△ABC的内角A,B,C的对边分别为a,b,c,A=π3,b=√2,求△ABC的面积.【解答】取②acosB=bsinA,由正弦定理可得:sinAacosB=sinBsinA≠0,∴tanB=1,B∈(0, π),∴B=π4.∴C=π−A−B=5π12,sinC=sin(π3+π4)=√32×√22+12×√22=√6+√24.由正弦定理可得:asinπ3=√2sinπ4,解得a=√3.∴△ABC的面积S=12×√3×√2×√6+√24=3+√34.18.如图,五面体ABCDEF中,正方形ABCD的边长为2√2,AB=2EF,EF // 平面ABCD,点P在线段DE上,且DP=2PE,Q为BC的中点.(1)求证:BE // 平面APQ ;(2)已知AE ⊥平面ABCD ,且AE =2,求二面角P −AF −E 的余弦值. 【解答】连结BD ,交AQ 于点M ,连结PM ,∵△BMQ ∼△DMA ,BQ =12AD ,∴BM =12DM , ∵EP =12DP ,∴PM // BE , ∵PM ⊂平面APQ ,BE ⊄平面APQ , ∴BE // 平面APQ .以A 为坐标原点,分别以AB →,AD →,AE →为x 轴,y 轴,z 轴,建立空间直角坐标系, 则A(0, 0, 0),C(2√2, √2, 0),D(0, 2√2, 0),E(0, 0, 2),F(√2, 0, 2), 设P(x, y, z),∵DP =2PE ,∴DP →=23DE →,则(x, y −2√2, z)=23(0, −2√2, 2),则P(0, 2√23, 43),∴AP→=(0, 2√23, 43), 设平面AFP 的法向量为n →=(x, y, z), ∵AF →=(√2, 0, 2),∴{AF →⋅n →=√2x +2z =0AP →⋅n →=2√23y +43z =0 ,取x =√2,则n →=(√2,√2,−1), 平面AEF 的法向量m →=(0, 1, 0), 设二面角P −AF −E 的平面角为θ, 则cosθ=|n →⋅m →||n →|⋅|m →|=√105. ∴二面角P −AF −E 的余弦值为√105.19.数学家也有一些美丽的错误,如法国数学家费马于1640年提出了以下猜想:F n=22n+1(n∈N)是质数.1732年,瑞士数学家欧拉算出F5=641×6700417,该数不是质数.已知S n为数列{a n}的前n项和,且S n=log2(F n−1)−1(n∈N+)(1)求数列{a n}的通项公式;(2)若b n=(n+1)log2a n+1,设为数列{2b n}的前n项和,求出T n,并证明:对任意n∈N+,1≤T n< 2.【解答】S n=log2(F n−1)−1=log222n−1=2n−1,当n=1时,a1=S1=1,n≥2时,a n=S n−S n−1=2n−1−2n−1+1=2n−1,对n=1也成立,则a n=2n−1,n∈N∗;b n=(n+1)log2a n+1=(n+1)log22n=n(n+1),2 b n =2n(n+1)=2(1n−1n+1),则T n=2(1−12+12−13+⋯+1n−1n+1)=2(1−1n+1),由于2(1−1n+1)随着n的增大而增大,可得T1≤T n<2,即对任意n∈N+,1≤T n<2.20.截止到2018年末,我国公路总里程达到484.65万公里,其中高速公路达到14.26万公里,规模居世界第一.与此同时,行车安全问题也成为管理部门关注的重点.如图是某部门公布的一年内道路交通事故成因分析,由图可知,超速驾驶已经成为交通事故的一个主要因素.研究表明,急刹车时的停车距离等于反应距离与制动距离的和,下表是根据某部门的调查结果整理所得的数据(v表示行车速度,单位:km/ℎ;d1,d2分别表示反应距离和制动距离,单位:m)道路交通事故成因分析(1)从一年内发生的道路交通事故中随机抽出3起进行分析研究,求其中恰好有1起属于超速驾驶的概率(用频率代替概率);(2)已知d 2与v 的平方成正比,且当行车速度为100km/ℎ时,制动距离为65m .(i)由表中数据可知,d 1与v 之间具有线性相关关系,请建立d 1与v 之间的回归方程,并估计车速为110km/ℎ时的停车距离;(ii)我国《道路交通安全法》规定:车速超过100km/ℎ时,应该与同车道前车保持100m 以上的距离,请解释一下上述规定的合理性.参考数据:∑=i=110 vi 1004,∑=i=110 (d1)i 210,∑(i=110 vi d 1)i =22187.3,∑=i=110 vi 2106054,1103352524≈0.21参考公式:对于一组数据(x 1, y 1),(x 2, y 2),…,(x n , y n ),其回归直线y =b x +a 的斜率和截距的最小二乘估计分别为:b =∑ n i=1(x i −x ¯)(y i −y ¯)∑ n i=1(x i −x ¯)2,a =y ¯−b x ¯.【解答】由题意知,P i =C 3i ⋅(15)i ⋅(1−15)3−i , 故所求的概率为P 1=C 31⋅15⋅(45)2=48125;由d 2与v 的平方成正比,设d 2=kv 2,当行车速度为v =100km/ℎ时,制动距离为d 2=65m ; 即k ⋅1002=65,解得k =0.0065, 所以d 2=0.0065v 2;(i)由d 1与v 之间具有线性相关关系,且v ¯=110∑ 10i=1v i=110×1004=100.4,d 1¯=110∑ 10i=1(d 1)i =110×210=21;又∑(i=110 vi d 1)i =22187.3,∑=i=110 vi 2106054,1103352524≈0.21, 所以b =∑ n i=1(x i −x ¯)(y i −y ¯)∑ n i=1(x i −x ¯)2=∑ 10i=1v i ⋅(d 1)i −10v ¯⋅d i ¯∑)i=110 (vi 2−10v ¯2=22187.3−10×100.4×21106054−10×100.4=1103352524≈0.21,a =d 1¯−b v ¯=21−0.21×100.4=−0.084, 所以d 1与v 间的回归方程为d 1̂=0.21v −0.084; v =110时,d 1̂=0.21×110−0.084=23.016. d 2=0.0065×1102=78.65,所以估计车速为110km/ℎ时的停车距离为d =23.016+78.65=101.666≈102(m);(ii)v =100时,d 1̂=0.21×100−0.084=20.916. d 2=0.0065×1002=65,车速为100km/ℎ时的停车距离为d =20.916+65=85.916≈86(m); 车速超过100km/ℎ时,考虑到车速增加后刹车距离也随着增大, 要保证行车安全,车辆应该与同车道前车保持在100m 以上的距离.21.已知F 1,F 2分别为椭圆C:x 2a 2+y 2b 2=1(a >b >0)的左、右焦点,P 为C 上的动点,其中P 到F 1的最短距离为1,且当△PF 1F 2的面积最大时,△PF 1F 2恰好为等边三角形. (1)求椭圆C 的标准方程;(2)以椭圆长轴为直径的圆叫做椭圆的“外切圆”,记椭圆C 的外切圆为E . (i)求圆E 的方程;(ii)在平面内是否存在定点Q ,使得以PQ 为直径的圆与E 相切,若存在求出定点Q 的坐标;若不存在,请说明理由 【解答】由题意可得:a −c =1,面积最大时P 为短轴的顶点,再由△PF 1F 2恰好为等边三角形,可得b =√32⋅2c ,a 2=b 2+c 2, 解得:a 2=4,b 2=3, 所以椭圆的标准方程为:x 24+y 23=1;(i)由(1)得圆E 的圆心坐标为(0, 0),半径为a =2, 所以圆E 的方程为:x 2+y 2=4; (ii)解法一:假设存在满足条件的定点Q ,由题意可知定点Q 必在x 轴上,设Q(m, 0),P(x 0, y 0),则x 024+y 023=1,由(i)可知,圆E 的圆心为坐标原点O ,半径为2,设以PQ 为直径的圆的圆心为G ,半径为r ,则G 为线段PQ 的中点, r =|PQ|2,即G(x 0+m 2, y 02),r =12√(x 0−m)2+y 02,因为圆E 与圆G 相切,则|OG|=2−r ,所以√(x 0+m 2)2+y 024=2−12√(x 0−m)2+y 02,其中y 02=3−34x 02,两边平方并整理得:4−mx 0=2√(x 0−m)2+y 02,化简得(m 2−1)(x 02−4)=0,上式对任意x 0∈[−2, 2]恒成立, 故m 2−1=0,解得m =±1,所以,当定点Q 恰好为椭圆的焦点时,符合题意.解法二:存在满足条件的定点Q,由题意可知,定点Q必在x轴上,设Q(m, 0),P(x0, y0),则x024+y023=1,由(i)可知,圆E的圆心为坐标原点O,半径为2,设以PQ为直径的圆的圆心为G,半径为r,则G为线段PQ的中点,则r=|PQ|2,即G(x0+m2, y02),r=12√(x0−m)2+y02,因为圆E与圆G相切,则|OG|=2−r,所以√(x0+m2)2+y024=2−12√(x0−m)2+y02,整理得√(x0+m)2+y02+√(x0−m)2+y02=4,设Q′(−m, 0),则|PQ′|+|PQ|=4,又因为P在椭圆x 24+y23=1上,设F1,F2分别为椭圆的左右焦点,|PF1|+|PF2|=4,故Q,Q′分别与F1,F2重合,所以当定点Q恰好为椭圆的C的焦点时,符合题意.解法三:假设存在满足条件的定点Q,由题意可知定点Q必在x轴上,由(i)可知,圆E的圆心为坐标原点O,半径为2,设以PQ为直径的圆的圆心为G,半径为r,则G为线段PQ的中点,则r=|PQ|2,因为圆E与圆G相切,则|OG|=2−r,即|OG|=2−|PQ|2,所以2|OG|+|PQ|=4,设Q′为Q关于原点对称点,则OG恰好为△QQ′P的中位线,所以2|OG|=|PQ′|,所以|PQ′|+|PQ|=4,下同解法二;解法四:假设存在满足条件的定点Q,设M(m, n),P(x0, y0),则x024+y023=1由(i)可知,圆E的圆心为坐标原点O,半径为2,设以PQ为直径的圆的圆心为G,半径为r,则G为线段PQ的中点,则r=|PQ|2,即G(x0+m2, y0+n2),r=12√(x0−m)2+(y0−n)2,因为圆E与圆G相切,则|OG|=2−r,所以√(x0+m)24+(y0+n)24=2−12√(x0−m)2+(y0−n)2整理得√(x0+m)2+(y0+n)2+√(x0−m)2+(y0−n)2=4,设Q(−m, −n),因此|PQ′|+|PQ|=4,下同解法一.22.已知函数f(x)=lnxx +k的极大值为1+ee,其中e=2.71828…为自然对数的底数.(1)求实数k的值;(2)若函数g(x)=e x−ax,对任意x∈(0, +∞),g(x)≥af(x)恒成立.(i)求实数a的取值范围;(ii)证明:x2f(x)>asinx+x2−1.【解答】f′(x)=1−lnxx2,x>0,当x∈(0, e)时,f′(x)>0,f(x)递增;当x∈(e, +∞)时,f′(x)<0,f(x)递减;所以f(x)的极大值为f(e)=1e +k=1e+1,故k=1;(i)根据题意,任意x∈(0, +∞),g(x)≥af(x),即e x−ax ≥alnxx+a,化简得xe x−alnx−ax−a≥0,令ℎ(x)=xe x−alnx−ax−a,x>0,ℎ(x)=e lnx e x−alnx−ax−a=e lnx+x−a(lnx+x)−a,令lnx+x=t,t∈R,设H(t)=e t−at−a,H′(t)=e t−a,只需H(t)≥0,t∈R,当a<0时,当t<0时,H(t)<1−at−a,所以H(1a −1)<1−a(1a−1)−a=0,不成立;当a=0时,H(t)≥0显然成立;当a>0时,由H′(t)=e t−a,当t∈(−∞, lna),H(t)递减,t∈(lna, +∞),H(t)递增,H(t)的最小值为H(lna)=a−alna−a=−alna,由H(lna)=−alna≥0,得0<a≤1,综上0≤a≤1;(ii)证明:要证x2f(x)>asinx+x2−1,只需证明x2(lnxx+1)>asinx+x2+1,化简得xlnx+1>asinx,只需证lnx+1x >asinxx,设F(x)=lnx+1x,G(x)=x−sinx,由F′(x)=1x −1x2=x−1x2,当x∈(0, 1)时,F(x)递减;x∈(1, +∞)时,F(x)递增;所以F(x)≥F(1)=1,由G′(x)=1−cosx≥0,G(x)在(0, +∞)递增,故G(x)>G(0)=0,得x>sinx,又由(i)0≤a≤1,所以asinxx<1,所以F(x)>asinxx成立,故原命题成立.。
济南市2019届高三上学期期末考试试题(数学文)

高三年级学习质量评估文科数学试题本试卷共6页,23题(含选考题),全卷满分150分。
考试用时120分钟。
注意事项:1.答题前,先将自己的姓名、准考证号填写在试卷和答题卡上,并将准考证号条形码粘贴在答题卡的指定位置上。
2.选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
写在试卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用黑色签字笔直接答在答题卡上对应的答题区域内。
写在试卷、草稿纸和答题卡上的非答题区域均无效。
4.选考题的作答:先把所选题目的题号在答题卡上指定的位置用2B 铅笔涂黑。
答案写在答题卡上对应的答题区域内,写在试卷、草稿纸和答题卡上的非答题区域均无效。
5.考试结束后,请将本试卷和答题卡一并上交。
参考公式:锥体的体积公式:13V Sh =(其中S 为锥体的底面积,h 为锥体的高) 球体的体积公式:343V R π=(其中R 为球体的半径)一、选择题:本题共12小题,每小题5分。
共60分。
在每小题给出的四个选项中。
只有一项是符合题目要求的。
1.已知集合{}{}1,11,A x x B x A B =>-=-≤≤⋂=则 A .{}01,B. {}1x x >-C .{}11x x -<≤D .{}11x x -≤≤2.已知复数z 满足2z z i +⋅=(其中i 为虚数单位),则z 的虚部为 A. 1- B .1 C .i - D .i3.已知等差数列{}n a 的前n 项和S n ,若2358,25a a S +==,则该数列的公差为 A.-2B .2C.-3D .34.已知实数,x y 满足约束条件0,33,20,x x y z x y y ≥⎧⎪+≤=+⎨⎪≥⎩则的最大值是A.0B.1C.5D.65.已知命题p :关于m 的不等式2log m <1的解集为{}2m m <;函数q :函数()321f x x x =+-在区间(0,1)内有零点.下列命题为真命题的是 A. p q ∧B .()p q ∧⌝C. ()p q ⌝∧D .()()p q ⌝∧⌝6.如图,在△ABC 中,90,2C AC BC ∠===o,三角形内的空白部分由三个半径均为1的扇形构成,向△ABC 内随机投掷一点,则该点落在阴影部分的概率为 A.8πB .4π C. 18π-D .14π-7.已知双曲线2221y x b-=,其焦点到渐近线的距离为2,则该双曲线的离心率为A.2B.3C.2D.58.函数()2ln 8x y x =-的图象大致为9.为了得到函数2cos 2y x =的图象,可以将函数cos 23sin 2y x x =-的图象A.向左平移6π个单位长度 B.向右平移6π个单位长度 C.向左平移3π个单位长度D. 向右平移3π个单位长度10.如图,网络纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的体积是 A. 18π B. 21π C. 27π D. 36π11.执行如图所示的程序框图,若输入的,,a b c 依次为()()()sin cos sin sin ,sin ,cos 42αααππαααα⎛⎫∈ ⎪⎝⎭,其中,,则输出的x 为A .()cos cos ααB .()sin sin αα C .()cos sin αα D .()sin cos αα12.我国南宋数学家杨辉所著的《详解九章算法》一书中记录了一个由正整数构成的三角形数表,我们通常称之为杨辉三角.以下数表的构造思路就来源于杨辉三角.从第二行起,每一行中的数字均等于其“肩上”两数之和,表中最后一行仅有一个数a ,则a 的值为 A. 100820182⨯B .100920182⨯C. 100820202⨯D .100920202⨯二、填空题:本题共4小题,每小题5分。
2019年山东省济南市高三(上)期末数学试卷

2019年山东省济南市高三(上)期末数学试卷一、选择题(共8题,每题5分)1.(2019秋•济南期末)已知集合A={x|x2﹣x﹣6≤0},B={x|x﹣1<0},则A∪B=()A.(﹣∞,3]B.(﹣∞,2]C.(﹣∞,1)D.[﹣2,1)2.(2019秋•济南期末)若复数z满足z(1+i)=﹣2i(其中i为虚数单位),则z的共轭复数是()A.1﹣i B.1+i C.﹣1﹣i D.﹣1+i 3.(2019秋•济南期末)设x∈R,则“2x>4”是“lg(|x|﹣1)>0”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件4.(2019秋•济南期末)已知函数则函数y=f(1﹣x)的图象大致是()A.B.C.D.5.(2019秋•济南期末)若抛物线y2=2px(p>0)的焦点到准线的距离为2,过焦点的直线与抛物线交于A,B两点,且|AB|=8,则弦AB的中点到y轴的距离为()A.2B.3C.4D.66.(2019秋•济南期末)已知函数,则=()A.0B.C.1D.27.(2019秋•济南期末)考古发现,在埃及金字塔内有一组神秘的数字142857,因为142857×2=285714,142857×3=428571,…所以这组数字又叫走马灯数.该组数字还有如下规律:142+857=999,571+428=999,…若从1,4,2,8,5,7这6个数字中任意取出3个数字构成一个三位数x,则999﹣x的结果恰好是剩下3个数字构成的一个三位数的概率为()A.B.C.D.8.(2019秋•济南期末)若F为双曲线的左焦点,过原点的直线l与双曲线C的左右两支分别交于A,B两点,则﹣的取值范围是()A.B.C.D.二.多选题(共4小题)9.(2019秋•济南期末)习总书记讲到:“广大人民群众坚持爱国奉献,无怨无悔,让我感到千千万万普通人最伟大,同时让我感到幸福都是奋斗出来的”.某企业2019年12个月的收入与支出数据的折线图如下:已知:利润=收入﹣支出,根据该折线图,下列说法正确的是()A.该企业2019年1月至6月的总利润低于2019年7月至12月的总利润B.该企业2019年第一季度的利润约是60万元C.该企业2019年4月至7月的月利润持续增长D.该企业2019年11月份的月利润最大10.(2019秋•济南期末)声音是由物体振动产生的声波,其中包含着正弦函数.纯音的数学模型是函数y=A sinωt,我们听到的声音是由纯音合成的,称之为复合音.若一个复合音的数学模型是函数,则下列结论正确的是()A.2π是f(x)的一个周期B.f(x)在[0,2π]上有3个零点C.f(x)的最大值为D.f(x)在上是增函数11.(2019秋•济南期末)给定两个不共线的空间向量与,定义叉乘运算:.规定:①为同时与,垂直的向量;②,,三个向量构成右手系(如图1);③.如图2,在长方体ABCD﹣A1B1C1D1中,AB=AD=2,AA1=4,则下列结论正确的是()A.B.C.D.长方体ABCD﹣A1B1C1D1的体积12.(2019秋•济南期末)若实数a,b满足2a+3a=3b+2b,则下列关系式中可能成立的是()A.0<a<b<1B.b<a<0C.1<a<b D.a=b三.填空题(共14小题)13.(2019秋•济南期末)(2x﹣y)5的展开式中,含x3y2项的系数为80.(用数字作答).14.(2019秋•济南期末)已知,则tan2α=﹣4 15.(2019秋•济南期末)平行四边形ABCD中,M为CD的中点,点N满足,若,则λ+μ的值为.16.(2019秋•济南期末)如图,矩形ABCD中,,AD=2,Q为BC的中点,点M,N分别在线段AB,CD上运动(其中M不与A,B重合,N不与C,D重合),且MN∥AD,沿MN将△DMN折起,得到三棱锥D﹣MNQ,则三棱锥D﹣MNQ体积的最大值为1;当三棱锥D﹣MNQ体积最大时,其外接球的表面积的值为.四、解答题(共6题,共计70分)17.(2019秋•济南期末)在①,②a cos B=b sin A,③这三个条件中任选一个,补充在下面的问题中,并解决该问题.已知△ABC的内角A,B,C的对边分别为a,b,c,,,求△ABC的面积.18.(2019秋•济南期末)如图,五面体ABCDEF中,正方形ABCD的边长为,AB=2EF,EF∥平面ABCD,点P在线段DE上,且DP=2PE,Q为BC的中点.(1)求证:BE∥平面APQ;(2)已知AE⊥平面ABCD,且AE=2,求二面角P﹣AF﹣E的余弦值.19.(2019秋•济南期末)数学家也有一些美丽的错误,如法国数学家费马于1640年提出了以下猜想:(n∈N)是质数.1732年,瑞士数学家欧拉算出F5=641×6700417,该数不是质数.已知S n为数列{a n}的前n项和,且S n=log2(F n﹣1)﹣1(n∈N+)(1)求数列{a n}的通项公式;(2)若b n=(n+1)log2a n+1,设为数列的前n项和,求出T n,并证明:对任意n∈N+,1≤T n<2.20.(2019秋•济南期末)截止到2018年末,我国公路总里程达到484.65万公里,其中高速公路达到14.26万公里,规模居世界第一.与此同时,行车安全问题也成为管理部门关注的重点.如图是某部门公布的一年内道路交通事故成因分析,由图可知,超速驾驶已经成为交通事故的一个主要因素.研究表明,急刹车时的停车距离等于反应距离与制动距离的和,下表是根据某部门的调查结果整理所得的数据(v表示行车速度,单位:km/h;d1,d2分别表示反应距离和制动距离,单位:m)道路交通事故成因分析v6472808997105113121128135 d113.415.216.718.620.121.923.525.326.828.5(1)从一年内发生的道路交通事故中随机抽出3起进行分析研究,求其中恰好有1起属于超速驾驶的概率(用频率代替概率);(2)已知d2与v的平方成正比,且当行车速度为100km/h时,制动距离为65m.(i)由表中数据可知,d1与v之间具有线性相关关系,请建立d1与v之间的回归方程,并估计车速为110km/h时的停车距离;(ii)我国《道路交通安全法》规定:车速超过100km/h时,应该与同车道前车保持100m 以上的距离,请解释一下上述规定的合理性.参考数据:,,,,参考公式:对于一组数据(x1,y1),(x2,y2),…,(x n,y n),其回归直线的斜率和截距的最小二乘估计分别为:,.21.(2019秋•济南期末)已知F1,F2分别为椭圆(a>b>0)的左、右焦点,P为C上的动点,其中P到F1的最短距离为1,且当△PF1F2的面积最大时,△PF1F2恰好为等边三角形.(1)求椭圆C的标准方程;(2)以椭圆长轴为直径的圆叫做椭圆的“外切圆”,记椭圆C的外切圆为E.(i)求圆E的方程;(ii)在平面内是否存在定点Q,使得以PQ为直径的圆与E相切,若存在求出定点Q的坐标;若不存在,请说明理由22.(2019秋•济南期末)已知函数的极大值为,其中e=2.71828…为自然对数的底数.(1)求实数k的值;(2)若函数,对任意x∈(0,+∞),g(x)≥af(x)恒成立.(i)求实数a的取值范围;(ii)证明:x2f(x)>a sin x+x2﹣1.。
山东省济南市中学2019年高三数学文上学期期末试题含解析
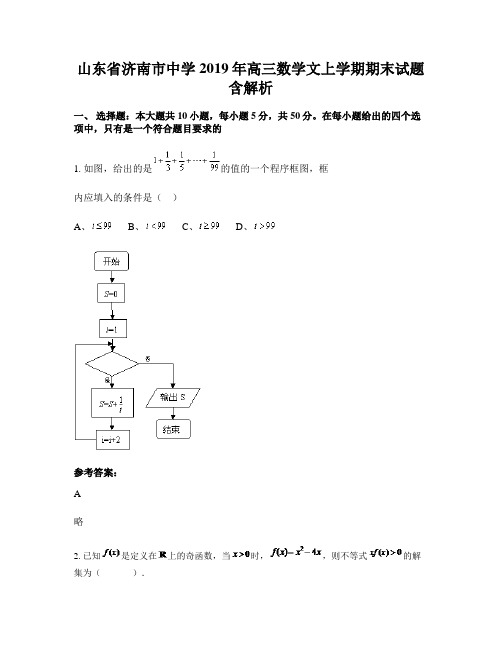
山东省济南市中学2019年高三数学文上学期期末试题含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 如图,给出的是的值的一个程序框图,框内应填入的条件是()A、 B、 C、 D、参考答案:A略2. 已知是定义在上的奇函数,当时,,则不等式的解集为().A.B.C.D.参考答案:A∵是定义在上的奇函数,当时,,∴当时,,当时,,当时,,∴不等式的解集为.故选.3. 某几何体的三视图如图所示,则该几何体的体积为()A.16π﹣B.16π﹣C.8π﹣D.8π﹣参考答案:D【考点】L!:由三视图求面积、体积.【分析】由三视图可知:该几何体为一个半圆柱挖取一个倒立的四棱锥.【解答】解:由三视图可知:该几何体为一个半圆柱挖取一个倒立的四棱锥.∴该几何体的体积V=﹣=8π﹣.故选:D.4. 设随机变量服从正态分布N(3,4),若,则实数a的值为A. B. C. D.参考答案:A略5. 含有三个实数的集合可表示为{a,,1},也可表示为{a2, a+b,0},则a2011+b2011的值为()A.0 B.1 C.-1 D.±1参考答案:C6. 已知集合,,,则P的真子集共有()A. 0个B. 1个C. 2个D. 3个参考答案:B【分析】先求得两个集合的交集,然后计算出真子集的个数.【详解】依题意,其真子集为,只有一个真子集,故选B.【点睛】本小题主要考查两个集合交集的运算,考查真子集的个数,属于基础题.7. (5分)(2015?嘉兴二模)在△ABC中,“sinA>cosB”是“△ABC为锐角三角形”的()A.充分不必要条件 B.必要不充分条件C.充要条件 D.既不充分也不必要条件参考答案:B【考点】:必要条件、充分条件与充要条件的判断.【专题】:简易逻辑.【分析】:根据充分条件和必要条件的定义结算三角函数的性质进行判断即可.解:若B为钝角,A为锐角,则sinA>0,cosB<0,则满足sinA>cosB,但△ABC为锐角三角形不成立,若△ABC为锐角三角形,则A,B,π﹣A﹣B都是锐角,即π﹣A﹣B<,即A+B>,B>﹣A,则cosB<cos(﹣A),即cosB<sinA,故“sinA>cosB”是“△ABC为锐角三角形”的必要不充分条件,故选:B【点评】:本题主要考查充分条件和必要条件的判断,根据三角形的性质是解决本题的关键.8. 右图是函数y=A sin(ωx+φ)(,)图像的一部分.为了得到这个函数的图像,只要将y=sin x(x∈R)的图像上所有的点()A.向左平移个单位长度,再把所得各点的横坐标缩短到原来的,纵坐标不变.B.向左平移个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变.C.向左平移个单位长度,再把所得各点的横坐标缩短到原来的,纵坐标不变.D.向左平移个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变.参考答案:A9. 已知集合,集合,则()A. B.C. D.参考答案:D试题分析:因,则,故,故应选D.考点:不等式的解法与集合的运算.10. 已知向量,,则下列向量中与垂直的是()A. B. C.D.参考答案:D二、填空题:本大题共7小题,每小题4分,共28分11. 某次测量发现一组数据具有较强的相关性,并计算得,其中数据因书写不清,只记得是任意一个值,则该数据对应的残差的绝对值不大于1的概率为___.(残差=真实值-预测值)参考答案:12. 已知A(﹣1,4),B(3,﹣2),以AB为直径的圆的标准方程为.参考答案:(x﹣1)2+(y﹣1)2=13【考点】J1:圆的标准方程.【分析】因为线段AB为所求圆的直径,所以利用中点坐标公式求出线段AB的中点即为所求圆的圆心坐标,再利用两点间的距离公式求出圆心C与点A之间的距离即为所求圆的半径,根据求出的圆心坐标与半径写出圆的标准方程即可.【解答】解:设圆心为C,∵A(﹣1,4),B(3,﹣2),∴圆心C的坐标为(1,1);∴|AC|==,即圆的半径r=,则以线段AB为直径的圆的方程是(x﹣1)2+(y﹣1)2=13.故答案为:(x﹣1)2+(y﹣1)2=13.【点评】此题考查了中点坐标公式,两点间的距离公式以及圆的标准方程,解答本题的关键是灵活运用已知条件确定圆心坐标及圆的半径.同时要求学生会根据圆心与半径写出圆的标准方程.13. 已知G为△ABC的重心,令,,过点G的直线分别交AB、AC于P、Q两点,且,,则= .参考答案:3考点:平面向量的基本定理及其意义.专题:平面向量及应用.分析:显然,根据G点为重心,从而可以用表示,而和共线,从而,而已知,从而会最后得到关于的式子:,从而得到,两式联立消去x即可求出答案.解答:解:如图,=;∴;G为△ABC的重心;∴,;∴;整理得,;∴;消去x得,;∴.故答案为:3.点评:考查向量加法、减法的几何意义,共线向量基本定理,重心的性质:重心到顶点距离是它到对边中点距离的2倍,以及向量加法的平行四边形法则,向量的加法、减法运算,平面向量基本定理.14. 已知定义在R上的函数对任意的都满足,当时,,若函数只有4个零点,则取值范围是.参考答案:15. 四边形ABCD中,∠BAC=90°,BD+CD=2,则它的面积最大值等于.参考答案:【考点】三角形中的几何计算.【分析】由题意,当D在BC的正上方时S△DBC面积最大,A为BC的正下方时S△ABC面积最大,设BC为2x,可求DH=,S四边形ABCD=x2+x,设x=sinθ,则利用三角函数恒等变换的应用化简可得S四边形= [1+sin(2θ﹣)],利用正弦函数的性质即可求得S四边形的最大值.【解答】解:∵∠BAC=90°,BD+CD=2,∴D在以BC为焦点的椭圆上运动,A在以BC为直径的圆上运动,∴当D在BC的正上方时S△DBC面积最大,A为BC的正下方时S△ABC面积最大,此时,设BC 为2x,则DH=,∴S四边形ABCD=S△BCD+S ABC=x+=x2+x,设x=sinθ,则=cosθ,∴S四边形=sin2θ+sinθcosθ=(2sin2θ+2sinθcosθ)=(1﹣cos2θ+sin2θ)=[1+sin(2θ﹣)],∴当sin(2θ﹣)=1时,即θ=时,S四边形取得最大值,最大值为:.故答案为:.16. 在三角形中,已知的面积为,则的长为_ 参考答案:略17. 已知函数f(x)的定义域为R,若存在常数m>0,对任意x∈R,有|f(x)|≤m|x|,则称函数f(x)为F﹣函数.给出下列函数:①f(x)=x2;②f(x)=;③f(x)=2x;④f(x)=sin2x.其中是F﹣函数的序号为.参考答案:②④【考点】绝对值不等式;函数的值域.【专题】计算题;新定义.【分析】本题是一个新定义的题目,故依照定义的所给的规则对所四个函数进行逐一验证,选出正确的即可.【解答】解:对于①,|f(x)|<m|x|,显然不成立,故其不是F﹣函数.对于②f(x)=,|f(x)|==≤1×|x|,故函数f(x)为F﹣函数.对于③f(x)=2x ,|f(x)|<m|x|,显然不成立,故其不是F函数.对于④f(x)=sin2x,由于|f(x)|=|sin2x|≤|2x|=2|x|,故函数f(x)为F﹣函数.故答案为②④.【点评】本题考查根据所给的新定义来验证函数是否满足定义中的规则,是函数知识的给定应用题,综合性较强,做题时要注意运用所深知识灵活变化进行证明,属于中档题,属于创新型题.三、解答题:本大题共5小题,共72分。
2019届山东省济南市高三上学期期末考试数学(文)试题(解析版)

2019届山东省济南市高三上学期期末考试数学(文)试题一、单选题1. 已知集合, , 则( )A. B.C. D.【答案】C【解析】利用交集概念与运算直接求解即可.【详解】∵集合, ,∴故选:C【点睛】本题考查交集的概念及运算, 属于基础题.2.已知复数满足(其中为虚数单位), 则的虚部为( )A. -1B. 1C.D.【答案】A【解析】利用复数的乘除运算化简复数z, 结合虚部概念得到答案.【详解】由z(1+i)=2, 得,∴复数z的虚部是﹣1.故选:A.【点睛】本题考查复数代数形式的乘除运算, 考查了复数的基本概念, 是基础题.3.已知等差数列的前项和为, 若, , 则该数列的公差为( )A. -2B. 2C. -3D. 3【答案】B【解析】利用等差数列的通项公式与求和公式即可得出.【详解】由题意可得: 5 d=25,解得d=2.故选:B.【点睛】本题考查了等差数列的通项公式与求和公式, 考查了推理能力与计算能力, 属于基础题.4.已知实数, 满足约束条件则的最大值是( )A. 0B. 1C. 5D. 6【答案】D【解析】由约束条件作出可行域, 化目标函数为直线方程的斜截式, 由直线方程可知, 要使z最大, 则直线在y轴上的截距最大, 结合可行域可知当直线z=x+2y过点A时z 最大, 求出A的坐标, 代入z=x+2y得答案.【详解】解: 画出约束条件表示的平面区域, 如图所示;由解得A(0, 3),此时直线y x z在y轴上的截距最大,所以目标函数z=x+2y的最大值为zmax=0+2×3=6.故选:D.【点睛】本题考查了简单的线性规划, 考查数形结合的思想, 解答的关键是正确作出可行域, 是中档题.5.已知命题关于的不等式的解集为;命题函数在区间内有零点, 下列命题为真命题的是( )A. B. C. D.【答案】C【解析】先判断命题p, q的真假, 结合真值表可得结果.【详解】关于的不等式的解集为, 故命题p为假命题,由函数可得: 即,结合零点存在定理可知在区间内有零点, 故命题求为真命题.∴p∧q为假, 为假, 为真, 为假,故选:C.【点睛】本题考查的知识点是复合命题的真假, 其中判断出命题p与q的真假是解答本题的关键.6.如图, 在中, , , 三角形内的空白部分由三个半径均为1的扇形构成, 向内随机投掷一点, 则该点落在阴影部分的概率为( )A. B. C. D.【答案】D【解析】由题意, 概率符合几何概型, 所以只要求出阴影部分的面积, 根据三角形的内角和得到空白部分的面积是以1为半径的半圆的面积, 由几何概型的概率公式可求.【详解】由题意, 题目符合几何概型,中, , , , 所以三角形为直角三角形, 面积为, 阴影部分的面积为:三角形面积圆面积=2 ,所以点落在阴影部分的概率为;故选: D.【点睛】本题考查了几何概型的概率求法;关键明确概率模型, 然后求出满足条件的事件的集合, 由概率公式解答.7.已知双曲线, 其焦点到渐近线的距离为2, 则该双曲线的离心率为( )A. B. C. 2 D.【答案】D【解析】由焦点到条渐近线的距离, 可得b=1, 求出c, 即可求出双曲线的离心率.【详解】解: 双曲线的焦点到条渐近线的距离等于 b.∵双曲线的焦点到条渐近线的距离为2,∴b=2, 又a∴c=,∴e.故选: D.【点睛】本题考查双曲线的性质, 考查学生的计算能力, 求出双曲线的焦点到条渐近线的距离等于b是关键.8. 函数的图象大致为( )A. B. C. D.【答案】D【解析】利用函数的奇偶性, 极限, 特值点逐一判断即可.【详解】由函数为偶函数, 排除B选项,当x 时, , 排除A选项,当x= 时, , 排除C选项,故选:D【点睛】函数图象的辨识可从以下方面入手: (1)从函数的定义域, 判断图象的左右位置;从函数的值域, 判断图象的上下位置;(2)从函数的单调性, 判断图象的变化趋势;(3)从函数的奇偶性, 判断图象的对称性;(4)从函数的特征点, 排除不合要求的图象. 9.为了得到函数的图象, 可以将函数的图象( )A. 向左平移个单位长度B. 向右平移个单位长度C. 向左平移个单位长度D. 向右平移个单位长度【答案】B【解析】利用函数y=Acos(ωx+φ)的图象变换规律, 得出结论.【详解】解:为了得到函数的图象, 可以将函数向右平移个单位长度,故选:B.【点睛】本题主要考查函数y=Acos(ωx+φ)的图象变换规律, 属于基础题.10.如图, 网络纸上小正方形的边长为1, 粗实线画出的某几何体的三视图, 则该几何体的体积是( )A. B. C. D.【答案】A【解析】根据三视图知几何体是组合体: 下面是圆锥、上面是四分之一球, 根据图中数据, 代入体积公式求值即可.【详解】解: 根据三视图知几何体是组合体,下面是圆锥、上面是四分之一球,圆锥的底面半径为3, 高为3;球的半径为3,∴该几何体的体积V ,故选:A.【点睛】本题考查由三视图求几何体的体积, 以及几何体的体积公式, 考查空间想象能力, 三视图正确复原几何体是解题的关键.11.执行如图所示的程序框图, 若输入的, , 依次为, , , 其中, 则输出的为( )A. B. C. D.【答案】C【解析】由框图可知程序的功能是输出三者中的最大者, 比较大小即可.【详解】由程序框图可知a、b、c中的最大数用变量x表示并输出,∵∴,又在R上为减函数, 在上为增函数,∴<, <故最大值为, 输出的为故选:C【点睛】本题主要考查了选择结构. 算法是新课程中的新增加的内容, 也必然是新高考中的一个热点, 应高度重视. 程序填空也是重要的考试题型, 这种题考试的重点有: ①分支的条件②循环的条件③变量的赋值④变量的输出.12.我国南宋数学杨家辉所著的《详解九章算法》一书中记录了一个由正整数构成的三角形数表, 我们通常称之为杨辉三角.以下数表的构造思路就来源于杨辉三角.从第二行起, 每一行中的数字均等于其“肩上”两数之和, 表中最后一行仅有一个数, 则的值为( )A. B. C. D.【答案】C【解析】根据每一行的第一个数的变化规律即可得到结果.【详解】解: 第一行第一个数为: ;第二行第一个数为: ;第三行第一个数为: ;第四行第一个数为: ;,第n行第一个数为: ;一共有1010行,∴第1010行仅有一个数: ;故选:C.【点睛】本题考查了由数表探究数列规律的问题, 考查学生分析解决问题的能力, 属于中档题.二、填空题13. 已知向量, 为单位向量, 若与的夹角为, 则__________.【答案】1【解析】根据条件可以得到, 这样便可求出的值, 从而得出的值.【详解】解: 根据条件, , ;∴1-1+1=1;∴.故答案为: .【点睛】本考查单位向量的概念, 向量数量积的运算及其计算公式, 求向量的长度的方法: 求.14.过圆内一点作直线, 则直线被圆所截得的最短弦长为__________.【答案】【解析】化已知圆为标准方程, 得到圆心C(1, 0), 半径r=2, 利用垂径定理结合题意, 即可求出最短弦长.【详解】圆方程可化为(x﹣1)2+y2=4,∴圆心C(1, 0), 半径r=2, ,当截得的弦长最短时, CP⊥l, 即P为弦的中点,∴最短弦长为故答案为: .【点睛】本题主要考查直线和圆的位置关系, 最短弦长问题, 考查数形结合思想, 属于基础题. 15.在正方形中, 点, 分别为, 的中点, 将四边形沿翻折, 使得平面平面, 则异面直线与所成角的余弦值为__________.【答案】【解析】连接FC, 与DE交于O点, 取BE中点为N, 连接ON, CN, 易得ON∥BD, 故∠CON 就是异面直线与所成角, 在等腰三角形CON中, 求底角的余弦值即可.【详解】连接FC, 与DE交于O点, 取BE中点为N,连接ON, CN, 易得ON∥BD∴∠CON就是异面直线与所成角设正方形的边长为2,OC= , ON= , CN=∴cos∠CON==故答案为:【点睛】本题主要考查异面直线所成的角问题,难度一般. 求异面直线所成角的步骤:1平移,将两条异面直线平移成相交直线. 2定角,根据异面直线所成角的定义找出所成角. 3求角,在三角形中用余弦定理或正弦定理或三角函数求角. 4结论.16.若函数与的图象交点的横坐标之和为2, 则的值为__________.【答案】1【解析】根据函数的对称性得出直线过曲线的对称中心, 从而得出m的值.【详解】解: ∵y= 的图象均关于点(1, 0)对称,∴函数的图象关于点(1, 0)对称, 且在上单调递增,∵函数与的图象交点的横坐标之和为2,∴直线y=经过点(1, 0),∴m=1.故选:1.【点睛】本题考查了函数对称性的判断与应用, 属于中档题.三、解答题17. 已知的内角, , 的对边分别为, , , 且.(1)求角的大小;(2)若, , 边的中点为, 求的长.【答案】(1)(2)【解析】(1)由及正弦定理得, 从而得到角的大小;(2)利用可得, 进而利用余弦定理可得, 再利用余弦定理可得BD.【详解】(1)由及正弦定理得: ,又, 所以,因为所以,因为, 所以.(2)由余弦定理得,所以, 所以,因为,所以,所以.【点睛】本题主要考查了正弦定理, 余弦定理的综合应用, 解题时注意分析角的范围.对于余弦定理一定要熟记两种形式: (1);(2).另外, 在解与三角形、三角函数有关的问题时, 还要记住, , 等特殊角的三角函数值, 以便在解题中直接应用. 18.如图, 在三棱锥中, 是边长为2的等边三角形, .(1)求证: ;(2)若, , 为线段上一点, 且, 求三棱锥的体积.【答案】(1)详见解析(2)【解析】(1)取中点, 连接, , 先证明, , 可得平面, 即可得证;(2)利用等积法即可得到结果.【详解】(1)证明: 取中点, 连接, ,因为, 所以,因为为等边三角形, 所以,又因为, 所以平面,因为平面, 所以.(2)因为, 所以,又因为, , 所以平面,因为为边长为2的等边三角形, 所以,因为,所以.【点睛】等积法: 等积法包括等面积法和等体积法. 等积法的前提是几何图形(或几何体)的面积(或体积)通过已知条件可以得到, 利用等积法可以用来求解几何图形的高或几何体的高, 特别是在求三角形的高和三棱锥的高时, 这一方法回避了通过具体作图得到三角形(或三棱锥)的高, 而通过直接计算得到高的数值.19. 某企业生产了一种新产品, 在推广期邀请了100位客户试用该产品, 每人一台.试用一个月之后进行回访, 由客户先对产品性能作出“满意”或“不满意”的评价, 再让客户决定对性能满意对性能不满意合计是否购买该试用产品(不购买则可以免费退货, 购买则仅需付成本价).经统计,决定退货的客户人数是总人数的一半,“对性能满意”的客户比“对性能不满意”的客户多10人,“对性能不满意”的客户中恰有选择了退货.(1)请完成下面的列联表, 并判断是否有的把握认为“客户购买产品与对产品性能满意之间有关”.购买产品不购买产品合计(2)企业为了改进产品性能, 现从“对性能不满意”的客户中按是否购买产品进行分层抽样, 随机抽取6位客户进行座谈.座谈后安排了抽奖环节, 共有4张奖券, 奖券上分别印有200元、400元、600元和800元字样, 抽到奖券可获得相应奖金.6位客户有放回的进行抽取, 每人随机抽取一张奖券, 求6位客户中购买产品的客户人均所得奖金不少于500元的概率.附:, 其中0.1500.1000.0500.0250.0102.072 2.7063.841 5.024 6.635【答案】(1)详见解析(2)详见解析【解析】(1) 根据题意填写列联表, 由表中数据计算观测值, 对照临界值得出结论;(2)利用古典概型概率公式即可得到结果.【详解】(1)设“对性能不满意”的客户中购买产品的人数为,对性能满意对性能不满意合计则退货的人数为,由此可列出下表购买产品50不购买产品50合计100因为, 所以;填写列联表如下:对性能满意对性能不满意合计购买产品351550不购买产品203050合计5545100所以.所以, 有的把握认为“客户购买产品与对产品性能满意之间有关”. (2)由题意知:参加座谈的购买产品的人数为2, 退货的人数为4. “购买产品的客户抽取奖券”的基本事件有:, , , , , , , , , , , , , , , , 共有16个基本事件:设事件“购买产品的客户人均所得奖金不少于500元”,则事件包含的基本事件有:, , , , , , , , , , 共有10个基本事件:则.所以, 购买产品的客户人均所得奖金不少于500元的概率是.【点睛】本题考查了独立性检验和列举法求古典概型的概率问题, 是基础题.20.已知椭圆过点, 左焦点为.(1)求椭圆的方程;(2)已知直线与椭圆有两个不同的交点, , 点, 记直线, 的斜率分别为, , 求的取值范围.【答案】(1)(2)【解析】(1)由题意布列a, b的方程组, 解之即可得到椭圆的方程;(2)联立直线与椭圆方程可得, 利用韦达定理表示, 利用二次函数的性质即可得到结果.【详解】(1)因为左焦点为, 所以,因为过点, 所以,解之得, , 所以椭圆方程为.(2)设, ,联立方程, 得,由,,,,,所以,因为, 所以,所以取值范围为.【点睛】圆锥曲线中最值与范围问题的常见求法: (1)几何法, 若题目的条件和结论能明显体现几何特征和意义, 则考虑利用图形性质来解决;(2)代数法, 若题目的条件和结论能体现一种明确的函数关系, 则可首先建立目标函数, 再求这个函数的最值. 在利用代数法解决最值与范围问题时常从以下几个方面考虑: ①利用判别式来构造不等关系, 从而确定参数的取值范围;②利用隐含或已知的不等关系建立不等式, 从而求出参数的取值范围;③利用基本不等式求出参数的取值范围;④利用函数的值域的求法, 确定参数的取值范围.21. 已知函数.(1)若曲线在点处切线的斜率为1, 求实数的值;(2)当时, 恒成立, 求实数的取值范围.【答案】(1)(2)【解析】(1)求出, 令x=1,即可解出实数的值;(2)时, 恒成立转化为求函数最小值大于零即可.【详解】(1),因为, 所以;(2), 设,设, 设,注意到, ,(ⅰ)当时, 在上恒成立,所以在上恒成立, 所以在上是增函数,所以, 所以在上恒成立,所以在上是增函数,所以在上恒成立, 符合题意;(ⅱ)当时, , , 所以, 使得,当时, , 所以, 所以在上是减函数,所以在上是减函数,所以, 所以在上是减函数,所以, 不符合题意;综上所述: .【点睛】利用导数研究不等式恒成立或存在型问题, 首先要构造函数, 利用导数研究函数的单调性, 求出最值, 进而得出相应的含参不等式, 从而求出参数的取值范围;也可分离变量, 构造函数, 直接把问题转化为函数的最值问题.22.在平面直角坐标系中, 以坐标原点为极点,x轴的正半轴为极轴建立极坐标系, 曲线的极坐标方程为, 直线的参数方程为(为参数), 其中, 直线与曲线相交于, 两点.(1)求曲线的直角坐标方程;(2)若点满足, 求的值.【答案】(1)(2)【解析】(1)利用, 把极坐标方程化为直角坐标方程;(2)将直线的参数方程(为参数)代入, 得: ,利用韦达定理表示条件, 解方程即可得到结果.【详解】(1)由题意, 曲线的极坐标方程可化为: ,由得曲线的直角坐标方程为: .(2)将直线的参数方程(为参数)代入,得:,设, 对应的参数分别为, , 则, ,所以,解得或(舍),所以.【点睛】利用直线参数方程中参数的几何意义求解问题经过点P(x0, y0), 倾斜角为α的直线l的参数方程为 (t为参数). 若A, B为直线l上两点, 其对应的参数分别为, 线段AB的中点为M, 点M所对应的参数为, 则以下结论在解题中经常用到:(1) ;(2) ;(3) ;(4) .23. 已知函数.(1)当时, 求不等式的解集;(2)若对任意的恒成立, 求的取值范围.【答案】(1)(2)【解析】(1)当a=2时, 分类讨论求得不等式的解集;(2)对任意的恒成立即, 数形结合即可得到结果.【详解】(1)当时, , 即当时, 不等式等价于: ,解得, 所以;当时, 不等式等价于: ,解得, 所以;当时, 不等式等价于: ,解得, 所以;所以, 不等式的解集为.(2)由题意知, 当时, , 即恒成立,根据函数的图像易知,解得, 的取值范围为.【点睛】含绝对值不等式的解法有两个基本方法, 一是运用零点分区间讨论, 二是利用绝对值的几何意义求解. 法一是运用分类讨论思想, 法二是运用数形结合思想, 将绝对值不等式与函数以及不等式恒成立交汇、渗透, 解题时强化函数、数形结合与转化化归思想方法的灵活应用.。
2019年济南市高三数学上期末第一次模拟试卷附答案
2019年济南市高三数学上期末第一次模拟试卷附答案一、选择题1.程大位《算法统宗》里有诗云“九百九十六斤棉,赠分八子做盘缠.次第每人多十七,要将第八数来言.务要分明依次弟,孝和休惹外人传.”意为:996斤棉花,分别赠送给8个子女做旅费,从第一个开始,以后每人依次多17斤,直到第八个孩子为止.分配时一定要等级分明,使孝顺子女的美德外传,则第八个孩子分得斤数为( )A .65B .184C .183D .1762.设,x y 满足约束条件330280440x y x y x y -+≥⎧⎪+-≤⎨⎪+-≥⎩,则3z x y =+的最大值是( )A .9B .8C .3D .43.已知x ,y 满足2303301x y x y y +-≤⎧⎪+-≥⎨⎪≤⎩,z =2x +y 的最大值为m ,若正数a ,b 满足a +b =m ,则14a b +的最小值为( ) A .3B .32C .2D .52 4.在R 上定义运算:A ()1B A B =-,若不等式()x a -()1x a +<对任意的实数x ∈R 恒成立,则实数a 的取值范围是( ) A .11a -<< B .02a << C .1322a -<< D .3122a -<< 5.已知数列{}n a 的首项110,211n n n a a a a +==++,则20a =( )A .99B .101C .399D .4016.设变量,x y 、满足约束条件236y x x y y x ≤⎧⎪+≥⎨⎪≥-⎩,则目标函数2z x y =+的最大值为( )A .2B .3C .4D .97.数列{}n a 中,对于任意,m n N *∈,恒有m n m n a a a +=+,若118a =,则7a 等于( ) A .712 B .714 C .74 D .78 8.若直线2y x =上存在点(,)x y 满足30,230,,x y x y x m +-≤⎧⎪--≥⎨⎪≥⎩则实数m 的最大值为A .2-B .1-C .1D .39.设实数,x y满足242210x yx yx-≤⎧⎪+≤⎨⎪-≥⎩,则1yx+的最大值是()A.-1B.12C.1D.3210.设,x y满足约束条件0,20,240,x yx yx y-≥⎧⎪+-≥⎨⎪--≤⎩则2z x y=+的最大值为()A.2B.3C.12D.1311.在等差数列{}n a中,n S表示{}n a的前n项和,若363a a+=,则8S的值为()A.3B.8C.12D.2412.已知x,y均为正实数,且111226x y+=++,则x y+的最小值为()A.20B.24C.28D.32二、填空题13.等比数列{}n a的首项为1a,公比为q,1lim2nnS→∞=,则首项1a的取值范围是____________.14.如图,在ABCV中,,43C BCπ==时,点D在边AC上,AD DB=,DE AB⊥,E为垂足若22DE=,则cos A=__________15.设0a>,若对于任意满足8m n+=的正数m,n,都有1141a m n++≤,则a的取值范围是______.16.若x,y满足约束条件13x yx yxy-≥-⎧⎪+≤⎪⎨≥⎪⎪≥⎩,则2z x y=-的最大值是__________.17.已知x y 、满足约束条件1{1,22x y x y x y +≥-≥--≤若目标函数()0,0z ax by a b =+>>的最大值为7,则34a b+的最小值为_______. 18.若关于 x 的不等式 ()2221x ax -< 的解集中的整数恰有 3 个,则实数 a 的取值范围是________________.19.已知a b c R ∈、、,c 为实常数,则不等式的性质“a b a c b c >⇐+>+”可以用一个函数在R 上的单调性来解析,这个函数的解析式是()f x =_________20.设等比数列{}n a 满足a 1 + a 2 = –1, a 1 – a 3 = –3,则a 4 = ___________.三、解答题21.在ABC ∆中,角A 、B 、C 所对的边分别为a 、b 、c ,且满足sin cos 6b A a B π⎛⎫=- ⎪⎝⎭. (1)求角B 的大小;(2)若D 为AC 的中点,且1BD =,求ABC S ∆的最大值.22.如图,在四边形ABCD 中,7,2,AC CD AD ==2.3ADC π∠=(1)求CAD ∠的正弦值;(2)若2BAC CAD ∠=∠,且△ABC 的面积是△ACD 面积的4倍,求AB 的长.23.已知数列{}n a 中,11a =,121n n a a n +=+-,n n b a n =+.(1)求证:数列{}n b 是等比数列;(2)求数列{}n a 的前n 项和n S .24.记等差数列{}n a 的前n 项和为n S ,已知2446,10a a S +==.(Ⅰ)求数列{}n a 的通项公式;(Ⅱ)令2n n n b a =⋅*()n N ∈,求数列{}n b 的前n 项和n T .25.设ABC V 的内角A ,B ,C 的对边分别为a ,b ,c .若2cos cos cos c C a B b A =+. (1)求角C .(2)若ABC V 的面积为S ,且224()S b a c =--,2a =,求S .26.已知{}n a 是递增数列,其前n 项和为n S ,11a >,且10(21)(2)n n n S a a =++,*n ∈N . (Ⅰ)求数列{}n a 的通项n a ;(Ⅱ)是否存在*,,m n k N ∈使得2()m n k a a a +=成立?若存在,写出一组符合条件的,,m n k 的值;若不存在,请说明理由;(Ⅲ)设32n n n b a -=-,若对于任意的*n N ∈,不等式12111(1)(1)(1)n b b b ≤+++L m 的最大值.【参考答案】***试卷处理标记,请不要删除一、选择题1.B解析:B【解析】分析:将原问题转化为等差数列的问题,然后结合等差数列相关公式整理计算即可求得最终结果.详解:由题意可得,8个孩子所得的棉花构成公差为17的等差数列,且前8项和为996, 设首项为1a ,结合等差数列前n 项和公式有:811878828179962S a d a ⨯=+=+⨯=, 解得:165a =,则81765717184a a d =+=+⨯=.即第八个孩子分得斤数为184.本题选择B 选项.点睛:本题主要考查等差数列前n 项和公式,等差数列的应用,等差数列的通项公式等知识,意在考查学生的转化能力和计算求解能力.2.A解析:A【解析】绘制不等式组表示的平面区域如图所示,结合目标函数的几何意义可知目标还是在点()3,2C 处取得最大值,其最大值为max 33329z x y =+=+⨯=.本题选择A 选项.3.B解析:B【解析】【分析】作出可行域,求出m ,然后用“1”的代换配凑出基本不等式的定值,从而用基本不等式求得最小值.【详解】作出可行域,如图ABC ∆内部(含边界),作直线:20l x y +=,平移该直线,当直线l 过点(3,0)A 时,2x y +取得最大值6,所以6m =.1411414143()()(5)(5)6662b a b a a b a b a b a b a b +=++=++≥+⨯=,当且仅当4b a a b =,即12,33a b ==时等号成立,即14a b+的最小值为32. 故选:B.【点睛】 本题考查简单的线性规划,考查用基本不等式求最值,解题关键是用“1”的代换凑配出基本不等式的定值,从而用基本不等式求得最小值.4.C解析:C【解析】【分析】根据新运算的定义, ()x a -()x a +22x x a a =-++-,即求221x x a a -++-<恒成立,整理后利用判别式求出a 范围即可【详解】 Q A ()1B A B =-∴()x a -()x a +()()()()22=11x a x a x a x a x x a a --+=--+-=-++-⎡⎤⎣⎦ Q ()x a -()1x a +<对于任意的实数x ∈R 恒成立,221x x a a ∴-++-<,即2210x x a a -++--<恒成立,()()2214110a a ∴∆=-⨯-⨯--<,1322a ∴-<< 故选:C【点睛】本题考查新定义运算,考查一元二次不等式中的恒成立问题, 当x ∈R 时,利用判别式是解题关键5.C解析:C【解析】【分析】【详解】 由1211n n n a a a +=++,可得)211111111n n n n a a a a +++=+++=,, {}+1n a 是以1为公差,以1为首项的等差数列. 21,1n n a n a n +==-,即220201399a =-=.故选C.6.D解析:D【解析】【分析】由约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,联立方程组求得最优解的坐标,把最优解的坐标代入目标函数得结论.【详解】画出满足约束条件236y x x y y x ≤⎧⎪+≥⎨⎪≥-⎩的可行域,如图,画出可行域ABC ∆,(2,0)A ,(1,1)B ,(3,3)C ,平移直线2z x y =+,由图可知,直线2z x y =+经过(3,3)C 时目标函数2z x y =+有最大值,2z x y =+的最大值为9.故选D.【点睛】本题主要考查线性规划中,利用可行域求目标函数的最值,属于简单题.求目标函数最值的一般步骤是“一画、二移、三求”:(1)作出可行域(一定要注意是实线还是虚线);(2)找到目标函数对应的最优解对应点(在可行域内平移变形后的目标函数,最先通过或最后通过的顶点就是最优解);(3)将最优解坐标代入目标函数求出最值.7.D解析:D【解析】 因为11,8m n m n a a a a +=+=,所以2112,4a a == 42122a a ==,3123,8a a a =+= 73478a a a =+=.选D. 8.B解析:B【解析】【分析】首先画出可行域,然后结合交点坐标平移直线即可确定实数m 的最大值.【详解】不等式组表示的平面区域如下图所示,由2230y x x y =⎧⎨--=⎩,得:12x y =-⎧⎨=-⎩, 即C 点坐标为(-1,-2),平移直线x =m ,移到C 点或C 点的左边时,直线2y x =上存在点(,)x y 在平面区域内, 所以,m ≤-1,即实数m 的最大值为-1.【点睛】本题主要考查线性规划及其应用,属于中等题.9.D解析:D【解析】【分析】 由约束条件确定可行域,由1y x+的几何意义,即可行域内的动点与定点P (0,-1)连线的斜率求得答案.【详解】 由约束条件242210x y x y x -≤⎧⎪+≤⎨⎪-≥⎩,作出可行域如图,联立10220x x y -=⎧⎨+-=⎩,解得A (112,), 1y x+的几何意义为可行域内的动点与定点P (0,-1)连线的斜率, 由图可知,113212PA k +==最大. 故答案为32. 【点睛】 本题考查简单的线性规划,考查了数形结合的解题思想方法,属于中档题型.10.C解析:C【解析】【分析】 由约束条件可得可行域,将问题变成1122y x z =-+在y 轴截距最大问题的求解;通过平移直线可确定最大值取得的点,代入可得结果.【详解】由约束条件可得可行域如下图所示:当2z x y =+取最大值时,1122y x z =-+在y 轴截距最大 平移直线12y x =-,可知当直线1122y x z =-+过图中A 点时,在y 轴截距最大 由240y x x y =⎧⎨--=⎩得:()4,4A max 42412z ∴=+⨯= 故选:C【点睛】本题考查线性规划中最值问题的求解,关键是能够将问题转化为直线在y 轴截距最值问题的求解,属于常考题型.11.C解析:C【解析】【分析】由题意可知,利用等差数列的性质,得18363a a a a +=+=,在利用等差数列的前n 项和公式,即可求解,得到答案。
山东省济南市2019届高三上学期期末考试数学(理)试题(C卷)Word版含答案
山东省济南市2019届高三上学期期末考试数学(理)试题(C 卷)一、选择题(本大题共10个小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的)1、若集合2{|540}A x x x =++<,集合{|2}B x x =<-,则()R A C B 等于( )A .(2,1)--B .[2,4)-C .[2,1)--D .φ2、复数2(1)21i z i -+=+的实部为( ) A .2- B .1- C .1 D .03、从高一某班学号为150的50名学生中随机选取5名同学参加数学测试,采用系统抽样的方法,则所选5名学生的学号可能是( )A .2,11,23,34,45B .5,16,27,38,49C .3,13,25,37,47D .4,13,22,31,404、已知()f x 是奇函数,当0x >时,()21x a f x x +=⋅-,若()324f -=,则a 等于( ) A .-3 B .-2 C .-1 D .05、某几何体的三视图如图所示,则该几何体的体积是( ) A .43π B .53π C .223π+ D .243π+6、若函数()2sin(2)()2f x x πϕϕ=+<的图像向右平移6π个单位后经过点(,12π, 则ϕ 等于( )A .12π-B .6π-C .0D .6π 7、已知命题:(2,2),126p x x x ∃∈--++≥,则下列叙述正确的是( )A .p ⌝为::(2,2),126p x x x ∃∈--++<B .p ⌝为::(2,2),126p x x x ∀∈--++≥C .p ⌝为::(,2)(2,),126p x x x ∀∈-∞-+∞-++<D .p ⌝是真命题8、若实数,x y 满足不等式组202240250x y y x y -+≥⎧⎪+-≥⎨⎪-+≤⎩,且3()2(1)x a y -++的最大值为5,则a 等于( )A .-2B .-1C .2D .19、从焦点为F 的抛物线22(0)y px p =>上取一点000(,)()2p A x y x >做其准线的垂线,垂足为B ,若4,AF B =到直线AF的距离为 )A .22y x =B .23y x =C .24y x =D .26y x =10、已知函数()xf x e =,函数()5,44,4x ex xg x e x -≤⎧=⎨>⎩,对任意的[1,](1)x m m ∈>,都有()(2)f x g x -≤,则m 的取值范围是( )A .(1,22ln 2]+B .7(1,2ln 2]2+C .[ln 2,2)D .7(2,2ln 2)2+第Ⅱ卷二、填空题:本大题共4小题,每小题5分,共20分,把答案填在答题卷的横线上..11、已知向量(3,),(1,2)a m b ==-,若2a b b ⋅=,则m =12、5(3)(1x +的展开式中常数项为 14、如图是一个程序框图,则输出的n 的值是15、已知双曲线2222:1(0,0)x y C a b a b-=>>的右焦点为(,0)F c , 圆222:()F x c y c -+=,直线l 与双曲线C 的一条渐近线垂直且在x 轴上 的截距为23a ,若圆F 被直线l,则双曲线的离心率为16、若函数()()ln ()f x x b x b R =-∈在区间[1,]e 上单调递增,则实数b 的取值范围是三、解答题:本大题共6小题,满分70分,解答应写出文字说明、证明过程或演算步骤16、(本小题满分12分)在ABC ∆中,角,,A B C 所对的边分别为,,,2sin cos ,a b c A a B b ==(1)若2c =,求sin C ;(2)求ABC ∆面积的最大值.17、(本小题满分12分)如图,在梯形ABCD 中,0//,,60AB CD AD DC CB a ABC ===∠=,平面ACFE ⊥平面ABCD ,四边形ACFE 是矩形.(1)求证:BC ⊥平面ACFE ;(2)若A D A E =,求平面BDF 与平面ACFE 所成角的正弦值.18、(本小题满分12分)已知对边数列{}n a 的前n 项和为n S ,且12,,n n S a +成等差数列()n N *∈.(1)求a 的值及数列{}n a 的通项公式;(2)若21(1)log ()n n n b an a a +=-,求数列1{}nb 的前n 项和n T .19、(本小题满分12分)某公司为招聘新员工设计了一个面试方案:应聘者从6道备选试题中一次性随机抽取3道题,按照题目要求独立完成,规定:至少正确完成其中2道题的便可通过,已知6道备选题中应聘者甲有4道题能正确完成,2道题不能完成;应聘者乙每题正确完成的概率都是23,且每题正确完成与否互不影响.(1)分别求甲、乙两人正确完成面试题数的分布列及数学期望;(2)请分析比较甲、乙两人谁面试通过的可能性大?20、(本小题满分12分)已知函数()ln f x ax x =-,函数()31,3g x bx bx a R =-∈且0b ≠. (1)讨论函数()f x 的单调性;(2)若1a =,且对任意的1(1,2)x ∈,总存在2(1,2)x ∈,使()()120f x g x +=成立,求实数b 的取值范围.22、(本小题满分12分)已知11(,0),(,0)F c F c -分别是椭圆2222:1(0)x y G a b a b+=>>的左右焦点,点P 点, 且212123,2a PF F F PF PF ⊥-=. (1)求椭圆G 方程; (2)直线l 与椭圆G 交于两个不同的点,M N ,①若直线l 的斜率为1,且不经过椭圆G 上的点(4,)C n ,其中0n >,求证:直线CM 与CN 关于直线4x =对称.②若直线l 过2F ,点B 是椭圆G 的是上顶点,是否存在直线l ,使得2BF M ∆与2BF N ∆的面积的比值为2?如果存在,求出直线l 的方程;如果不存在,说明理由.。
2019年山东省济南市高三(上)期末数学试卷答案解析
2019年山东省济南市高三(上)期末数学试卷答案解析一、选择题(共8题,每题5分)1.(2019秋•济南期末)已知集合A={x|x2﹣x﹣6≤0},B={x|x﹣1<0},则A∪B=()A.(﹣∞,3]B.(﹣∞,2]C.(﹣∞,1)D.[﹣2,1)【解答】解:∵集合A={x|x2﹣x﹣6≤0}={x|﹣2≤x≤3},B={x|x﹣1<0}={x|x<1},∴A∪B={x|x≤3}=(﹣∞,3].故选:A.2.(2019秋•济南期末)若复数z满足z(1+i)=﹣2i(其中i为虚数单位),则z的共轭复数是()A.1﹣i B.1+i C.﹣1﹣i D.﹣1+i【解答】解:∵z(1+i)=﹣2i,∴z=,则.故选:D.3.(2019秋•济南期末)设x∈R,则“2x>4”是“lg(|x|﹣1)>0”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【解答】解:设x∈R,则“2x>4”⇒“lg(|x|﹣1)>0”,“lg(|x|﹣1)>0”⇒“x>2或x<﹣2”⇒“2x>4或”,∴“2x>4”是“lg(|x|﹣1)>0”的充分不必要条件.故选:A.4.(2019秋•济南期末)已知函数则函数y=f(1﹣x)的图象大致是()A.B.C.D.【解答】解:当x>0时,f(x)=xlnx,则令f′(x)=lnx+1=0,解得x=,所以当0<x<时,f(x)单调递减,x>时,f(x)单调递增,当x≤0时,f(x)=,则令f′(x)=e﹣x﹣1≥0,所以当x≤0时,f(x)单调递增,作出函数f(x)的图象如图:又因为f(1﹣x)的图象时将f(x)图象先关于y轴对称,再向左移动一个单位得到的,故根据f(x)图象可值f(1﹣x)图象为故选:B.5.(2019秋•济南期末)若抛物线y2=2px(p>0)的焦点到准线的距离为2,过焦点的直线与抛物线交于A,B两点,且|AB|=8,则弦AB的中点到y轴的距离为()A.2B.3C.4D.6【解答】解:抛物线y2=2px(p>0)的焦点到准线的距离为2,可得p=2,抛物线方程为:y2=4x,设A(x1,y1),B(x2,y2),根据抛物线定义,x1+x2+p=8,所以x1+x2=6,∵AB的中点的横坐标为:3,中点到y轴的距离为3,故选:B.6.(2019秋•济南期末)已知函数,则=()A.0B.C.1D.2【解答】解:根据题意,函数,则f(﹣x)=lg(﹣x)+=﹣lg(﹣x)+,则f(x)+f(﹣x)=1,则有=f(ln5)+f(﹣ln5)=1;故选:C.7.(2019秋•济南期末)考古发现,在埃及金字塔内有一组神秘的数字142857,因为142857×2=285714,142857×3=428571,…所以这组数字又叫走马灯数.该组数字还有如下规律:142+857=999,571+428=999,…若从1,4,2,8,5,7这6个数字中任意取出3个数字构成一个三位数x,则999﹣x的结果恰好是剩下3个数字构成的一个三位数的概率为()A.B.C.D.【解答】解:根据题意,从1,4,2,8,5,7这6个数字中任意取出3个数字构成一个三位数x,共有=6×5×4=120种.又因为从1,4,2,8,5,7这6个数字中:1+8=9,2+7=9,4+5=9,共3组.所以要使6个数字中任意取出3个数字构成一个三位数x,999﹣x的结果恰好是剩下3个数字构成的一个三位数,则每次抽取只能抽取一组数字中的一个,所以共有=6×4×2=48种,故.故选:C.8.(2019秋•济南期末)若F为双曲线的左焦点,过原点的直线l与双曲线C的左右两支分别交于A,B两点,则﹣的取值范围是()A.B.C.D.【解答】解:双曲线的a=2,b=,c=3,设|AF|=m,|FB|=n,F'为双曲线的右焦点,连接BF',AF',由对称性可得四边形AFBF'为平行四边形,可得|BF'|=|AF|=m,可得n﹣m=2a=4,n=m+4,且m≥c﹣a=1,则﹣=﹣,设f(m)=﹣,m≥1,f′(m)=﹣+=,当m>4时,f′(m)>0,f(m)递增,1≤m<4时,f′(m)<0,f(m)递减,可得f(m)在m=4处取得极小值,且为最小值﹣,当m=1时,f(1)=,当m→+∞时,f(m)→0,则f(m)∈[﹣,],故选:D.二.多选题(共4小题)9.(2019秋•济南期末)习总书记讲到:“广大人民群众坚持爱国奉献,无怨无悔,让我感到千千万万普通人最伟大,同时让我感到幸福都是奋斗出来的”.某企业2019年12个月的收入与支出数据的折线图如下:已知:利润=收入﹣支出,根据该折线图,下列说法正确的是()A.该企业2019年1月至6月的总利润低于2019年7月至12月的总利润B.该企业2019年第一季度的利润约是60万元C.该企业2019年4月至7月的月利润持续增长D.该企业2019年11月份的月利润最大【解答】解:由企业2019年12个月的收入与支出数据的折线图,得:在A中,该企业2019年1月至6月的总利润约为:x1=(30+40+35+30+50+60)﹣(20+25+10+20+22+30)=118,该企业2019年7月至12月的总利润约为:(80+75+75+80+90+80)﹣(28+22+30+40+45+50)=265,∴该企业2019年1月至6月的总利润低于2019年7月至12月的总利润,故A正确;在B中,该企业2019年第一季度的利润约约是:(30+40+35)﹣(20+25+10)=50万元,故B错误;在C中,该企业2019年4月至7月的月利润分别为(单位:万元):10,28,30,52,∴该企业2019年4月至7月的月利润持续增长,故C正确;在D中,该企业2019年7月和8月的月利润比11月份的月利润大,故D错误.故选:AC.10.(2019秋•济南期末)声音是由物体振动产生的声波,其中包含着正弦函数.纯音的数学模型是函数y=A sinωt,我们听到的声音是由纯音合成的,称之为复合音.若一个复合音的数学模型是函数,则下列结论正确的是()A.2π是f(x)的一个周期B.f(x)在[0,2π]上有3个零点C.f(x)的最大值为D.f(x)在上是增函数【解答】解:∵y=sin x的周期为2π,y=的周期为π,∴的周期为2π,故A正确;由=0,得sin x+sin x cos x=0,得sin x=0或cos x=﹣1,∵x∈[0,2π],∴x=0,x=π,x=2π,则f(x)在[0,2π]上有3个零点,故B正确;函数的最大值在[0,]上取得,由f′(x)=cos x+cos2x=2cos2x+cos x﹣1=0,可得cos x=,当x∈(0,)时,cos x 单调递减,原函数单调递增,当x∈(,)时,cos x单调递减,原函数单调递减,则当x=时,原函数求得最大值为sin+=,故C正确;∵f()=sin+=>1,f()=sin=1,∴f(x)在上不是增函数,故D错误.故选:ABC.11.(2019秋•济南期末)给定两个不共线的空间向量与,定义叉乘运算:.规定:①为同时与,垂直的向量;②,,三个向量构成右手系(如图1);③.如图2,在长方体ABCD﹣A1B1C1D1中,AB=AD=2,AA1=4,则下列结论正确的是()A.B.C.D.长方体ABCD﹣A1B1C1D1的体积【解答】解:∵,且分别与垂直,∴,故A正确;由题意,,,故B错误;∵,∴=,且与共线同向,∵,与共线同向,,与共线同向,∴||=,且与共线同向,故C正确;==2×2×4=16,故D成立.故选:ACD.12.(2019秋•济南期末)若实数a,b满足2a+3a=3b+2b,则下列关系式中可能成立的是()A.0<a<b<1B.b<a<0C.1<a<b D.a=b【解答】解:由2a+3a=3b+2b,设f(x)=2x+3x,g(x)=3x+2x,易知f(x),g(x)是递增函数,画出f(x),g(x)的图象如下:绿色,蓝色的分别是f(x),g(x)的图象,根据图象可知:当x=0,1时,f(x)=g(x),0<a<b<1,f(a)=f(b)可能成立;故A正确;当b<a<0时,因为f(x)≤g(x),所以f(a)=f(b)可能成立,B正确;当a=b时,显然成立,当1<a<b时,因为f(a)<g(b),所以不可能成立,故选:ABD.三.填空题(共14小题)13.(2019秋•济南期末)(2x﹣y)5的展开式中,含x3y2项的系数为80.(用数字作答).【解答】解:二项式(2x﹣y)5的展开式的通项为T r+1=25﹣r(﹣1)r C5r x5﹣r y r,令r=2,可得含x3y2的项的系数是23C52=80故答案为:80.14.(2019秋•济南期末)已知,则tan2α=﹣4【解答】解:由于,所以:,整理得:,所以:tan,则:=﹣4,故答案为:﹣4.15.(2019秋•济南期末)平行四边形ABCD中,M为CD的中点,点N满足,若,则λ+μ的值为.【解答】解:平行四边形ABCD中,M为CD的中点,点N满足,所以=+μ(),=+(),则根据平面向量基本定理可得,,解可得,λ=﹣1,μ=,则λ+μ=,故答案为:.16.(2019秋•济南期末)如图,矩形ABCD中,,AD=2,Q为BC的中点,点M,N分别在线段AB,CD上运动(其中M不与A,B重合,N不与C,D重合),且MN∥AD,沿MN将△DMN折起,得到三棱锥D﹣MNQ,则三棱锥D﹣MNQ体积的最大值为1;当三棱锥D﹣MNQ体积最大时,其外接球的表面积的值为.【解答】解:设MB=t,则AM=DN=2﹣t,∵沿MN将△DMN折起,当DN⊥平面MNQ时,三棱锥D﹣MNQ的体积最大,此时V D﹣MNQ===﹣,∴当t=时,V D﹣MNQ取最大值,最大值为1,此时MB=,DN=,∴MQ=NQ=2,∴△MNQ为等边三角形,∴当三棱锥D﹣MNQ体积最大时,三棱锥D﹣MNQ是正三棱柱的一部分,如图所示:则三棱柱MNQ﹣EDF的外接球即是三棱锥D﹣MNQ的外接球,设点G,H分别是上下地面正三角形的中心,∴线段GH的中点即是三棱柱MNQ﹣EDF的外接球的球心O,∴OH=又,∴△MNQ是边长为2的等边三角形,∴HQ=,∴三棱柱MNQ﹣EDF的外接球的半径R=OQ==,∴三棱锥D﹣MNQ的外接球的表面积为4πR2=,故答案为:1;.四、解答题(共6题,共计70分)17.(2019秋•济南期末)在①,②a cos B=b sin A,③这三个条件中任选一个,补充在下面的问题中,并解决该问题.已知△ABC的内角A,B,C的对边分别为a,b,c,,,求△ABC的面积.【解答】解:取②a cos B=b sin A,由正弦定理可得:sin Aa cos B=sin B sin A≠0,∴tan B=1,B∈(0,π),∴B=.∴C=π﹣A﹣B=,sin C=sin(+)=+=.由正弦定理可得:=,解得a=.∴△ABC的面积S=×=.18.(2019秋•济南期末)如图,五面体ABCDEF中,正方形ABCD的边长为,AB=2EF,EF∥平面ABCD,点P在线段DE上,且DP=2PE,Q为BC的中点.(1)求证:BE∥平面APQ;(2)已知AE⊥平面ABCD,且AE=2,求二面角P﹣AF﹣E的余弦值.【解答】解:(1)连结BD,交AQ于点M,连结PM,∵△BMQ~△DMA,BQ=,∴BM=,∵EP=,∴PM∥BE,∵PM⊂平面APQ,BE⊄平面APQ,∴BE∥平面APQ.(2)解:以A为坐标原点,分别以为x轴,y轴,z轴,建立空间直角坐标系,则A(0,0,0),C(,,0),D(0,2,0),E(0,0,2),F(,0,2),设P(x,y,z),∵DP=2PE,∴=,则(x,y﹣2,z)=(0,﹣2,2),则P(0,,),∴=(0,,),设平面AFP的法向量为=(x,y,z),∵=(,0,2),∴,取x=,则=(),平面AEF的法向量=(0,1,0),设二面角P﹣AF﹣E的平面角为θ,则cosθ==.∴二面角P﹣AF﹣E的余弦值为.19.(2019秋•济南期末)数学家也有一些美丽的错误,如法国数学家费马于1640年提出了以下猜想:(n∈N)是质数.1732年,瑞士数学家欧拉算出F5=641×6700417,该数不是质数.已知S n为数列{a n}的前n项和,且S n=log2(F n﹣1)﹣1(n∈N+)(1)求数列{a n}的通项公式;(2)若b n=(n+1)log2a n+1,设为数列的前n项和,求出T n,并证明:对任意n∈N+,1≤T n<2.【解答】解:(1)S n=log2(F n﹣1)﹣1=log22﹣1=2n﹣1,当n=1时,a1=S1=1,n≥2时,a n=S n﹣S n﹣1=2n﹣1﹣2n﹣1+1=2n﹣1,对n=1也成立,则a n=2n﹣1,n∈N*;(2)b n=(n+1)log2a n+1=(n+1)log22n=n(n+1),==2(﹣),则T n=2(1﹣+﹣+…+﹣)=2(1﹣),由于2(1﹣)随着n的增大而增大,可得T1≤T n<2,即对任意n∈N+,1≤T n<2.20.(2019秋•济南期末)截止到2018年末,我国公路总里程达到484.65万公里,其中高速公路达到14.26万公里,规模居世界第一.与此同时,行车安全问题也成为管理部门关注的重点.如图是某部门公布的一年内道路交通事故成因分析,由图可知,超速驾驶已经成为交通事故的一个主要因素.研究表明,急刹车时的停车距离等于反应距离与制动距离的和,下表是根据某部门的调查结果整理所得的数据(v表示行车速度,单位:km/h;d1,d2分别表示反应距离和制动距离,单位:m)道路交通事故成因分析v6472808997105113121128135 d113.415.216.718.620.121.923.525.326.828.5(1)从一年内发生的道路交通事故中随机抽出3起进行分析研究,求其中恰好有1起属于超速驾驶的概率(用频率代替概率);(2)已知d2与v的平方成正比,且当行车速度为100km/h时,制动距离为65m.(i)由表中数据可知,d1与v之间具有线性相关关系,请建立d1与v之间的回归方程,并估计车速为110km/h时的停车距离;(ii)我国《道路交通安全法》规定:车速超过100km/h时,应该与同车道前车保持100m 以上的距离,请解释一下上述规定的合理性.参考数据:,,,,参考公式:对于一组数据(x1,y1),(x2,y2),…,(x n,y n),其回归直线的斜率和截距的最小二乘估计分别为:,.【解答】解:(1)由题意知,P i=••,故所求的概率为P1=••=;(2)由d2与v的平方成正比,设d2=kv2,当行车速度为v=100km/h时,制动距离为d2=65m;即k•1002=65,解得k=0.0065,所以d2=0.0065v2;(i)由d1与v之间具有线性相关关系,且=v i=×1004=100.4,=(d1)i=×210=21;又,,,所以===≈0.21,=﹣=21﹣0.21×100.4=﹣0.084,所以d1与v间的回归方程为=0.21v﹣0.084;v=110时,=0.21×110﹣0.084=23.016.d2=0.0065×1102=78.65,所以估计车速为110km/h时的停车距离为d=23.016+78.65=101.666≈102(m);(ii)v=100时,=0.21×100﹣0.084=20.916.d2=0.0065×1002=65,车速为100km/h时的停车距离为d=20.916+65=85.916≈86(m);车速超过100km/h时,考虑到车速增加后刹车距离也随着增大,要保证行车安全,车辆应该与同车道前车保持在100m以上的距离.21.(2019秋•济南期末)已知F1,F2分别为椭圆(a>b>0)的左、右焦点,P为C上的动点,其中P到F1的最短距离为1,且当△PF1F2的面积最大时,△PF1F2恰好为等边三角形.(1)求椭圆C的标准方程;(2)以椭圆长轴为直径的圆叫做椭圆的“外切圆”,记椭圆C的外切圆为E.(i)求圆E的方程;(ii)在平面内是否存在定点Q,使得以PQ为直径的圆与E相切,若存在求出定点Q的坐标;若不存在,请说明理由【解答】解:(1)由题意可得:a﹣c=1,面积最大时P为短轴的顶点,再由△PF1F2恰好为等边三角形,可得b=,a2=b2+c2,解得:a2=4,b2=3,所以椭圆的标准方程为:+=1;(2)(i)由(1)得圆E的圆心坐标为(0,0),半径为a=2,所以圆E的方程为:x2+y2=4;(ii)解法一:假设存在满足条件的定点Q,由题意可知定点Q必在x轴上,设Q(m,0),P(x0,y0),则,由(i)可知,圆E的圆心为坐标原点O,半径为2,设以PQ为直径的圆的圆心为G,半径为r,则G为线段PQ的中点,r=,即G(,),r=,因为圆E与圆G相切,则|OG|=2﹣r,所以=2﹣,其中y02=3﹣x02,两边平方并整理得:4﹣mx0=2,化简得(m2﹣1)(x02﹣4)=0,上式对任意x0∈[﹣2,2]恒成立,故m2﹣1=0,解得m=±1,所以,当定点Q恰好为椭圆的焦点时,符合题意.解法二:存在满足条件的定点Q,由题意可知,定点Q必在x轴上,设Q(m,0),P(x0,y0),则,由(i)可知,圆E的圆心为坐标原点O,半径为2,设以PQ为直径的圆的圆心为G,半径为r,则G为线段PQ的中点,则r=,即G(,),r=,因为圆E与圆G相切,则|OG|=2﹣r,所以=2﹣,整理得,设Q′(﹣m,0),则|PQ′|+|PQ|=4,又因为P在椭圆上,设F1,F2分别为椭圆的左右焦点,|PF1|+|PF2|=4,故Q,Q′分别与F1,F2重合,所以当定点Q恰好为椭圆的C的焦点时,符合题意.解法三:假设存在满足条件的定点Q,由题意可知定点Q必在x轴上,由(i)可知,圆E的圆心为坐标原点O,半径为2,设以PQ为直径的圆的圆心为G,半径为r,则G为线段PQ的中点,则r=,因为圆E与圆G相切,则|OG|=2﹣r,即|OG|=2﹣,所以2|OG|+|PQ|=4,设Q′为Q关于原点对称点,则OG恰好为△QQ′P的中位线,所以2|OG|=|PQ′|,所以|PQ′|+|PQ|=4,下同解法二;解法四:假设存在满足条件的定点Q,设M(m,n),P(x0,y0),则由(i)可知,圆E的圆心为坐标原点O,半径为2,设以PQ为直径的圆的圆心为G,半径为r,则G为线段PQ的中点,则r=,即G (,),r=,因为圆E与圆G相切,则|OG|=2﹣r,所以=2﹣,整理得+=4,设Q(﹣m,﹣n),因此|PQ′|+|PQ|=4,下同解法一.22.(2019秋•济南期末)已知函数的极大值为,其中e=2.71828…为自然对数的底数.(1)求实数k的值;(2)若函数,对任意x∈(0,+∞),g(x)≥af(x)恒成立.(i)求实数a的取值范围;(ii)证明:x2f(x)>a sin x+x2﹣1.【解答】解:(1)f'(x)=,x>0,当x∈(0,e)时,f'(x)>0,f(x)递增;当x∈(e,+∞)时,f'(x)<0,f(x)递减;所以f(x)的极大值为f(e)=,故k=1;(2)(i)根据题意,任意x∈(0,+∞),g(x)≥af(x),即,化简得xe x﹣alnx﹣ax﹣a≥0,令h(x)=xe x﹣alnx﹣ax﹣a,x>0,h(x)=e lnx e x﹣alnx﹣ax﹣a=e lnx+x﹣a(lnx+x)﹣a,令lnx+x=t,t∈R,设H(t)=e t﹣at﹣a,H'(t)=e t﹣a,只需H(t)≥0,t∈R,当a<0时,当t<0时,H(t)<1﹣at﹣a,所以H()<1﹣a(﹣1)﹣a=0,不成立;当a=0时,H(t)≥0显然成立;当a>0时,由H'(t)=e t﹣a,当t∈(﹣∞,lna),H(t)递减,t∈(lna,+∞),H(t)递增,H(t)的最小值为H(lna)=a﹣alna﹣a=﹣alna,由H(lna)=﹣alna≥0,得0<a≤1,综上0≤a≤1;(ii)证明:要证x2f(x)>a sin x+x2﹣1,只需证明,化简得xlnx+1>a sin x,只需证,设F(x)=lnx+,G(x)=x﹣sin x,由F'(x)=,当x∈(0,1)时,F(x)递减;x∈(1,+∞)时,F(x)递增;所以F(x)≥F(1)=1,由G'(x)=1﹣cos x≥0,G(x)在(0,+∞)递增,故G(x)>G(0)=0,得x>sin x,又由(i)0≤a≤1,所以,所以F(x)>成立,故原命题成立.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高三年级学习质量评估文科数学试题一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合,,则( )A. B.C. D.【答案】C【解析】【分析】利用交集概念与运算直接求解即可.【详解】∵集合,,∴故选:C【点睛】本题考查交集的概念及运算,属于基础题.2.已知复数满足(其中为虚数单位),则的虚部为( )A. -1B. 1C.D.【答案】A【解析】【分析】利用复数的乘除运算化简复数z,结合虚部概念得到答案.【详解】由z(1+i)=2,得,∴复数z的虚部是﹣1.故选:A.【点睛】本题考查复数代数形式的乘除运算,考查了复数的基本概念,是基础题.3.已知等差数列的前项和为,若,,则该数列的公差为( )A. -2B. 2C. -3D. 3【答案】B【解析】【分析】利用等差数列的通项公式与求和公式即可得出.【详解】由题意可得:5d=25,解得d=2.故选:B.【点睛】本题考查了等差数列的通项公式与求和公式,考查了推理能力与计算能力,属于基础题.4.已知实数,满足约束条件则的最大值是( )A. 0B. 1C. 5D. 6【答案】D【解析】【分析】由约束条件作出可行域,化目标函数为直线方程的斜截式,由直线方程可知,要使z最大,则直线在y轴上的截距最大,结合可行域可知当直线z=x+2y过点A时z最大,求出A的坐标,代入z=x+2y得答案.【详解】解:画出约束条件表示的平面区域,如图所示;由解得A(0,3),此时直线y x z在y轴上的截距最大,所以目标函数z=x+2y的最大值为z max=0+2×3=6.故选:D.【点睛】本题考查了简单的线性规划,考查数形结合的思想,解答的关键是正确作出可行域,是中档题.5.已知命题关于的不等式的解集为;命题函数在区间内有零点,下列命题为真命题的是( )A. B. C. D.【答案】C【解析】【分析】先判断命题p,q的真假,结合真值表可得结果.【详解】关于的不等式的解集为,故命题p为假命题,由函数可得:即,结合零点存在定理可知在区间内有零点,故命题求为真命题.∴p∧q为假,为假,为真,为假,故选:C.【点睛】本题考查的知识点是复合命题的真假,其中判断出命题p与q的真假是解答本题的关键.6.如图,在中,,,三角形内的空白部分由三个半径均为1的扇形构成,向内随机投掷一点,则该点落在阴影部分的概率为( )A. B. C. D.【答案】D【解析】【分析】由题意,概率符合几何概型,所以只要求出阴影部分的面积,根据三角形的内角和得到空白部分的面积是以1为半径的半圆的面积,由几何概型的概率公式可求.【详解】由题意,题目符合几何概型,中,,,,所以三角形为直角三角形,面积为,阴影部分的面积为:三角形面积圆面积=2,所以点落在阴影部分的概率为;故选:D.【点睛】本题考查了几何概型的概率求法;关键明确概率模型,然后求出满足条件的事件的集合,由概率公式解答.7.已知双曲线,其焦点到渐近线的距离为2,则该双曲线的离心率为( )A. B. C. 2 D.【答案】D【解析】【分析】由焦点到条渐近线的距离,可得b=1,求出c,即可求出双曲线的离心率.【详解】解:双曲线的焦点到条渐近线的距离等于b.∵双曲线的焦点到条渐近线的距离为2,∴b=2,又a∴c=,∴e.故选:D.【点睛】本题考查双曲线的性质,考查学生的计算能力,求出双曲线的焦点到条渐近线的距离等于b是关键.8.函数的图象大致为( )A. B. C. D.【答案】D【解析】【分析】利用函数的奇偶性,极限,特值点逐一判断即可.【详解】由函数为偶函数,排除B选项,当x时,,排除A选项,当x=时,,排除C选项,故选:D【点睛】函数图象的辨识可从以下方面入手:(1)从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置;(2)从函数的单调性,判断图象的变化趋势;(3)从函数的奇偶性,判断图象的对称性;(4)从函数的特征点,排除不合要求的图象.9.为了得到函数的图象,可以将函数的图象( )A. 向左平移个单位长度B. 向右平移个单位长度C. 向左平移个单位长度D. 向右平移个单位长度【答案】B【解析】【分析】利用函数y=A cos(ωx+φ)的图象变换规律,得出结论.【详解】解:为了得到函数的图象,可以将函数向右平移个单位长度,故选:B.【点睛】本题主要考查函数y=A cos(ωx+φ)的图象变换规律,属于基础题.10.如图,网络纸上小正方形的边长为1,粗实线画出的某几何体的三视图,则该几何体的体积是( )A. B. C. D.【答案】A【解析】【分析】根据三视图知几何体是组合体:下面是圆锥、上面是四分之一球,根据图中数据,代入体积公式求值即可.【详解】解:根据三视图知几何体是组合体,下面是圆锥、上面是四分之一球,圆锥的底面半径为3,高为3;球的半径为3,∴该几何体的体积V,故选:A.【点睛】本题考查由三视图求几何体的体积,以及几何体的体积公式,考查空间想象能力,三视图正确复原几何体是解题的关键.11.执行如图所示的程序框图,若输入的,,依次为,,,其中,则输出的为( )A. B. C. D.【答案】C【解析】【分析】由框图可知程序的功能是输出三者中的最大者,比较大小即可.【详解】由程序框图可知a、b、c中的最大数用变量x表示并输出,∵∴,又在R上为减函数,在上为增函数,∴<,<故最大值为,输出的为故选:C【点睛】本题主要考查了选择结构.算法是新课程中的新增加的内容,也必然是新高考中的一个热点,应高度重视.程序填空也是重要的考试题型,这种题考试的重点有:①分支的条件②循环的条件③变量的赋值④变量的输出.12.我国南宋数学杨家辉所著的《详解九章算法》一书中记录了一个由正整数构成的三角形数表,我们通常称之为杨辉三角.以下数表的构造思路就来源于杨辉三角.从第二行起,每一行中的数字均等于其“肩上”两数之和,表中最后一行仅有一个数,则的值为( )A. B. C. D.【答案】C【解析】【分析】根据每一行的第一个数的变化规律即可得到结果.【详解】解:第一行第一个数为:;第二行第一个数为:;第三行第一个数为:;第四行第一个数为:;,第n行第一个数为:;一共有1010行,∴第1010行仅有一个数:;故选:C.【点睛】本题考查了由数表探究数列规律的问题,考查学生分析解决问题的能力,属于中档题.二、填空题(每题5分,满分20分,将答案填在答题纸上)13.已知向量,为单位向量,若与的夹角为,则__________.【答案】1【解析】【分析】根据条件可以得到,这样便可求出的值,从而得出的值.【详解】解:根据条件,,;∴1-1+1=1;∴.故答案为:.【点睛】本考查单位向量的概念,向量数量积的运算及其计算公式,求向量的长度的方法:求.14.过圆内一点作直线,则直线被圆所截得的最短弦长为__________.【答案】【解析】【分析】化已知圆为标准方程,得到圆心C(1,0),半径r=2,利用垂径定理结合题意,即可求出最短弦长.【详解】圆方程可化为(x﹣1)2+y2=4,∴圆心C(1,0),半径r=2,,当截得的弦长最短时,CP⊥l,即P为弦的中点,∴最短弦长为故答案为:.【点睛】本题主要考查直线和圆的位置关系,最短弦长问题,考查数形结合思想,属于基础题.15.在正方形中,点,分别为,的中点,将四边形沿翻折,使得平面平面,则异面直线与所成角的余弦值为__________.【答案】【解析】【分析】连接FC,与DE交于O点,取BE中点为N,连接ON,CN,易得ON∥BD,故∠CON就是异面直线与所成角,在等腰三角形CON中,求底角的余弦值即可.【详解】连接FC,与DE交于O点,取BE中点为N,连接ON,CN,易得ON∥BD∴∠CON就是异面直线与所成角设正方形的边长为2,OC=,ON=,CN=∴cos∠CON==故答案为:【点睛】本题主要考查异面直线所成的角问题,难度一般.求异面直线所成角的步骤:1平移,将两条异面直线平移成相交直线.2定角,根据异面直线所成角的定义找出所成角.3求角,在三角形中用余弦定理或正弦定理或三角函数求角.4结论.16.若函数与的图象交点的横坐标之和为2,则的值为__________.【答案】1 【解析】 【分析】根据函数的对称性得出直线过曲线的对称中心,从而得出m 的值.【详解】解:∵y=的图象均关于点(1,0)对称,∴函数的图象关于点(1,0)对称,且在上单调递增,∵函数与的图象交点的横坐标之和为2,∴直线y =经过点(1,0),∴m =1. 故选:1.【点睛】本题考查了函数对称性的判断与应用,属于中档题.三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.已知的内角,,的对边分别为,,,且.(1)求角的大小;(2)若,,边的中点为,求的长.【答案】(1)(2)【解析】 【分析】(1)由及正弦定理得,从而得到角的大小;(2)利用可得,进而利用余弦定理可得,再利用余弦定理可得BD.【详解】(1)由及正弦定理得:,又,所以,因为所以,因为,所以.(2)由余弦定理得,所以,所以,因为,所以,所以.【点睛】本题主要考查了正弦定理,余弦定理的综合应用,解题时注意分析角的范围.对于余弦定理一定要熟记两种形式:(1);(2).另外,在解与三角形、三角函数有关的问题时,还要记住,,等特殊角的三角函数值,以便在解题中直接应用.18.如图,在三棱锥中,是边长为2的等边三角形,.(1)求证:;(2)若,,为线段上一点,且,求三棱锥的体积.【答案】(1)详见解析(2)【解析】【分析】(1)先证明,,可得平面,即可得证;(2)利用等积法即可得到结果.【详解】(1)证明:取中点,连接,,因为,所以,因为为等边三角形,所以,又因为,所以平面,因为平面,所以.(2)因为,所以,又因为,,所以平面,因为为边长为2的等边三角形,所以,因为,所以.【点睛】等积法:等积法包括等面积法和等体积法.等积法的前提是几何图形(或几何体)的面积(或体积)通过已知条件可以得到,利用等积法可以用来求解几何图形的高或几何体的高,特别是在求三角形的高和三棱锥的高时,这一方法回避了通过具体作图得到三角形(或三棱锥)的高,而通过直接计算得到高的数值.19.某企业生产了一种新产品,在推广期邀请了100位客户试用该产品,每人一台.试用一个月之后进行回访,由客户先对产品性能作出“满意”或“不满意”的评价,再让客户决定是否购买该试用产品(不购买则可以免费退货,购买则仅需付成本价).经统计,决定退货的客户人数总人数的一半,“对性能满意”的客户比“对性能不满意”的客户多10人,“对性能不满意”的客户中恰有选择了退货.(1)请完成下面的列联表,并判断是否有的把握认为“客户购买产品与对产品性能满意之间有关”.对性能满意对性能不满意合计购买产品不购买产品合计(2)企业为了改进产品性能,现从“对性能不满意”的客户中按是否购买产品进行分层抽样,随机抽取6位客户进行座谈.座谈后安排了抽奖环节,共有4张奖券,奖券上分别印有200元、400元、600元和800元字样,抽到奖券可获得相应奖金.6位客户有放回的进行抽取,每人随机抽取一张奖券,求6位客户中购买产品的客户人均所得奖金不少于500元的概率.附:,其中0.150 0.100 0.050 0.025 0.0102.072 2.7063.841 5.024 6.635【答案】(1)详见解析(2)详见解析【解析】【分析】(1)根据题意填写列联表,由表中数据计算观测值,对照临界值得出结论;(2)利用古典概型概率公式即可得到结果.【详解】(1)设“对性能不满意”的客户中购买产品的人数为,则退货的人数为,由此可列出下表对性能满意对性能不满意合计购买产品50不购买产品50合计100因为,所以;填写列联表如下:对性能满意对性能不满意合计购买产品35 15 50不购买产品20 30 50合计55 45 100所以.所以,有的把握认为“客户购买产品与对产品性能满意之间有关”.(2)由题意知:参加座谈的购买产品的人数为2,退货的人数为4.“购买产品的客户抽取奖券”的基本事件有:,,,,,,,,,,,,,,,,共有16个基本事件:设事件“购买产品的客户人均所得奖金不少于500元”,则事件包含的基本事件有:,,,,,,,,,,共有10个基本事件:则.所以,购买产品的客户人均所得奖金不少于500元的概率是.【点睛】本题考查了独立性检验和列举法求古典概型的概率问题,是基础题.20.已知椭圆过点,左焦点为.(1)求椭圆的方程;(2)已知直线与椭圆有两个不同的交点,,点,记直线,的斜率分别为,,求的取值范围.【答案】(1)(2)【解析】【分析】(1)由题意布列a,b的方程组,解之即可得到椭圆的方程;(2)联立直线与椭圆方程可得,利用韦达定理表示,利用二次函数的性质即可得到结果.【详解】(1)因为左焦点为,所以,因为过点,所以,解之得,,所以椭圆方程为.(2)设,,联立方程,得,由,,,,,所以,因为,所以,所以取值范围为.【点睛】圆锥曲线中最值与范围问题的常见求法:(1)几何法,若题目的条件和结论能明显体现几何特征和意义,则考虑利用图形性质来解决;(2)代数法,若题目的条件和结论能体现一种明确的函数关系,则可首先建立目标函数,再求这个函数的最值.在利用代数法解决最值与范围问题时常从以下几个方面考虑:①利用判别式来构造不等关系,从而确定参数的取值范围;②利用隐含或已知的不等关系建立不等式,从而求出参数的取值范围;③利用基本不等式求出参数的取值范围;④利用函数的值域的求法,确定参数的取值范围.21.已知函数.(1)若曲线在点处切线的斜率为1,求实数的值;(2)当时,恒成立,求实数的取值范围.【答案】(1)(2)【解析】【分析】(1)求出,令x=1,即可解出实数的值;(2)时,恒成立转化为求函数最小值大于零即可.【详解】(1),因为,所以;(2),设,设,设,注意到,,(ⅰ)当时,在上恒成立,所以在上恒成立,所以在上是增函数,所以,所以在上恒成立,所以在上是增函数,所以在上恒成立,符合题意;(ⅱ)当时,,,所以,使得,当时,,所以,所以在上是减函数,所以在上是减函数,所以,所以在上是减函数,所以,不符合题意;综上所述:.【点睛】利用导数研究不等式恒成立或存在型问题,首先要构造函数,利用导数研究函数的单调性,求出最值,进而得出相应的含参不等式,从而求出参数的取值范围;也可分离变量,构造函数,直接把问题转化为函数的最值问题.(二)选考题:共10分.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.22.在平面直角坐标系中,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线的极坐标方程为,直线的参数方程为(为参数),其中,直线与曲线相交于,两点.(1)求曲线的直角坐标方程;(2)若点满足,求的值.【答案】(1)(2)【解析】【分析】(1)利用,把极坐标方程化为直角坐标方程;(2)将直线的参数方程(为参数)代入,得:,利用韦达定理表示条件,解方程即可得到结果.【详解】(1)由题意,曲线的极坐标方程可化为:,由得曲线的直角坐标方程为:.(2)将直线的参数方程(为参数)代入,得:,设,对应的参数分别为,,则,,所以,解得或(舍),所以.【点睛】利用直线参数方程中参数的几何意义求解问题经过点P(x0,y0),倾斜角为α的直线l的参数方程为(t为参数).若A,B为直线l上两点,其对应的参数分别为,线段AB的中点为M,点M所对应的参数为,则以下结论在解题中经常用到:(1) ;(2) ;(3) ;(4) .23.已知函数.(1)当时,求不等式的解集;(2)若对任意的恒成立,求的取值范围.【答案】(1)(2)【解析】【分析】(1)当a=2时,分类讨论求得不等式的解集;(2)对任意的恒成立即,数形结合即可得到结果.【详解】(1)当时,,即当时,不等式等价于:,解得,所以;当时,不等式等价于:,解得,所以;当时,不等式等价于:,解得,所以;所以,不等式的解集为.(2)由题意知,当时,,即恒成立,根据函数的图像易知,解得,的取值范围为.【点睛】含绝对值不等式的解法有两个基本方法,一是运用零点分区间讨论,二是利用绝对值的几何意义求解.法一是运用分类讨论思想,法二是运用数形结合思想,将绝对值不等式与函数以及不等式恒成立交汇、渗透,解题时强化函数、数形结合与转化化归思想方法的灵活应用.。
