毕业设计(论文)-预应力对高速旋转轮盘模态的影响分析[管理资料]
力学专业课程毕业论文高速回转圆盘的应力与应变理论分析

高速回转圆盘的应力与应变理论分析由于结构在真空环境下进行髙速的回转运动,在支撑、阻力的影响都忽略的情况下,首先想到结构是由于离心力的作用而发生的破坏。
目前工程上常用的计算髙速回转圆盘的方法有两种:一种是二次应力法,它是将圆盘简化为平面应力问题来求解,列出力平衡的微分方程;另一种方法是采用有限元法。
一、轮盘应力分析的一般理论回转圆盘的应力应该是三向应力,即径向应力周向应力轴向应力但由于轴向应力通常较径向应力和周向应力小得多,可认为回转圆盘仅受两向应力而把轴向应力 O■。
略去不计。
对于轴向厚度小于外直径1/4的薄圆盘是比较合适的。
图所示圆盘,盘的内半径为心,外半径为尺°,厚度y比外半径要小得多,且随半径r 而变化。
当该盘以角速度回转①在回转圆盘上切岀一个微块,当圆盘以角速度血旋转时,该微块的离心力为dp = dm・厂ar = pdV ・ rco" = pyrco^drdO图x・x变厚度圆盘在离心力作用下受力分析 a)对微元体进行受力分析:微元体所受到的载荷:①上表而径向力小②下表面径向力碍:③轴向载荷久④离心力dpb)对微元体列写平衡方程:de dy d0 7 ?(er,. + —— Jr)(y +—Jr)(r + dr)dO一a r yrdO一2(r&ydrsin ——+ pyrco^drdO = 0 dr dr 2由于是一个微量,所以sin —2 2 整理上式,并略去髙阶微量得E / x E (du咕口7(6*>刁乔七 刃=(% + 〃£)=__r —+“1 一“1一〃 "经化简,并令如得即为任意不等厚回转圆盘在离心力作用下产生变形的微分方程。
二.几种特殊情况2.1等厚度盘对于等厚度盘,尸常量,因此—=0,叫翌=0 dr dr 于是d^it 1 du u一 + ------ -- — = -Ardr r dr 厂几何方程: 物理方程:(2,2)(2,4)f 1 丄〃(In y)) du 'M(ln y) _ 1 L lrdr ) drk rdrr 2 丿(2,5)(2,6)将上式代入式d 2u= -Ar或者1 cl(ur)= -Ar积分得“ =—d/+c/+£i,式中G G为积分常数。
电动四轮割草机核心部件预应力模态分析

电动四轮割草机核心部件预应力模态分析
本文主要介绍电动四轮割草机的核心部件——刀盘轴承的预应力模态分析。
刀盘轴承
是电动四轮割草机的重要部件之一,它直接关系到割草机的工作效率和稳定性。
预应力在
轴承内部的作用是保证轴承在工作过程中具有足够的刚度和精度,可以承受来自外部的载荷。
同时,预应力也对轴承的寿命、运行精度和旋转平稳性等方面产生重要的影响。
因此,进行预应力模态分析具有一定的理论意义和实际应用价值。
首先,利用ANSYS软件建立电动四轮割草机的三维有限元模型,包括刀盘轴承和相关
连接件等部件。
然后,将轴承受到的外部载荷设置为10N,对模型进行模态分析,得到其
自然频率和振型。
模态分析结果表明,刀盘轴承在预应力状态下具有稳定的振动模态和较高的自然频率。
在模态振型中,轴承内部的各个部件都没有出现明显的振动和变形,轴承内部的预应力起
到了很好的稳定作用。
此外,轴承的自然频率也比较高,表明其在工作过程中具有较好的
稳定性和抗干扰能力。
通过这些分析结果,可以发现预应力在刀盘轴承中的重要性,也突显了电动四轮割草
机的结构稳定性和可靠性。
在实际应用中,需要注意对轴承进行预应力调整和检测,以确
保其具有良好的工作性能和可靠性。
同时,还可以通过对不同外部载荷下的模态分析,进
一步了解轴承的工作特性和受力情况。
旋转叶片的预应力模态分析
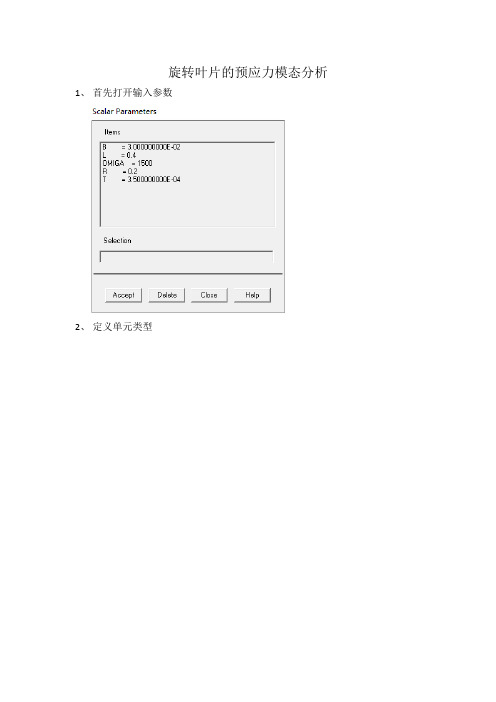
旋转叶片的预应力模态分析1、首先打开输入参数2、定义单元类型点击add选择shell选择181单元3、定义材料点Material Models输入材料的弹性模量和泊松比输入材料的密度4、输入shell单元的截面点击add/edit输入上面定义的参数T5、生成关键点点in active cs,出现如下图框一次输入四个关键点点apply输入第四个关键点,点Ok,如下图所示四个关键点6、生成面点area->arbitrary->Through KPs一次选编号为1,2,3,4的关键点,点击OK,生成如下图的面7、划分网格点MeshTool点Global->set,设置面单元的大小输入0.005后,点击Ok。
点击Mesh,选择上面建好的面点OK,生成单元可以查看生成的shell单元厚度8、求解选择分析类型选择静态分析点击Ok9、激活预应力选项勾选Calculate prestress effects点击Ok10、添加位移约束对线L4进行全约束选择线,点OK 弹出点OK11、添加转速点OK12、求解可以得到其应力图13、进行模态分析选择模态求解器点OK对模态进行选项分析14、进行模态求解可以查看前五阶的频率***** INDEX OF DATA SETS ON RESULTS FILE *****SET TIME/FREQ LOAD STEP SUBSTEP CUMULATIVE1 46.571 1 1 12 155.97 1 2 23 182.01 1 3 34 247.33 1 4 45 305.27 1 5 5第一阶阵型图第二阶阵型图第三阶阵型图第四阶阵型图第五阶阵型图15、转速为OMIGA=1000是模态分析前五阶模态***** INDEX OF DATA SETS ON RESULTS FILE *****SET TIME/FREQ LOAD STEP SUBSTEP CUMULATIVE1 197.73 1 1 12 213.60 1 2 23 365.38 1 3 34 712.52 1 4 45 727.64 1 5 5第一阶阵型图第二阶阵型图第三阶阵型图第四阶阵型图第五阶阵型图。
基于快速预测模型的轮盘瞬态变形影响

0 引言
发动机燃油消耗率增加。此外,与稳态相比,在瞬态
为了达到设计点的工作状态,航空发动机需要优 加速过程中发动机工作线更容易接近喘振线,带来了
化加速或减速路径,从而引入了瞬态性能的概念。在 较大的喘振风险 。 [3-4] 转子在离心力作用下,通常加
瞬态条件下,主流道参数急剧变化,气体与固体之间 速时更容易与机匣涂层发生碰摩,而过度碰磨会造成
发生剧烈热量交换,称为热浸润。例如从慢车到最大 叶片开裂、涂层脱落等故障,增大发动机失效风险[5]。
状态的瞬态加速,发动机机ห้องสมุดไป่ตู้必须适应新的稳态工作 可见如果能够获得瞬态叶尖间隙变化规律,可以为优
温度,通常会吸收 30% 的燃料能量[1]。热浸润的作用 化发动机性能特性和降低发动机故障风险提供一种
结果之一是使发动机结构尺寸如叶尖及封严间隙发 途径[6]。
文献标识码:A
doi:10.13477/ki.aeroengine.2021.04.012
Transient Deformations of Turbine Rotor based on a Reduced Prediction Method
MA Xiao-jian,HUANG Jing-jie,XU Ru-xue,ZHI Shao-qiang (AECC Shenyang Engine Research Institute,Shenyang 110015,China) Abstract:In order too predict disc deformations in preliminary design,a reduced method based on finite volume method was pro⁃ posed ,and the prediction code was prepared in Mat-lab platform. The method was used to simulate the heat soakage processes and tran⁃ sient deformations of turbine disc in the transient acceleration of a single shaft engine. Analyses indicated that the method was promising and adaptable. Results indicate that different parameters have different influences. The temperature level of the disc was influenced by heat transfer coefficient and time interval. The radial thermal gradient was flattened by high thermal conductivity,while initial temperature deter⁃ mined the centre and middle temperature of the disc. A well-designed profile could lower the stresses significantly compared to a disc with uniform width. The results of the deformation predictions under specific conditions show that different factors have different influence. Ini⁃ tial temperature result in maximum of 65% deviation,while heat transfer coefficient and time interval lead to 10% change. For a disc with a uniform width or constant material properties,the prediction results of derofmations are increased by 8.8% and 8.3%. Key words:turbine disc deformation;transient operation;blade tip clearance;simplified model;single shaft engine
预应力匝道桥梁体偏移扭转模型分析

预应力匝道桥梁体偏移扭转模型分析摘要:曲线上的预应力匝道桥梁体由于自身重力、温度力、预应力、收缩徐变的作用,使梁体产生偏移和扭转,甚至内弧侧支座脱空,桥面横坡发生变化。
这不仅对梁体受力不利,而且威胁到行车安全。
本文采用Midas/Civil软件,用梁格法建立有限元模型,对偏移、扭转的原因进行深入分析。
关键词:匝道桥、自身重力、温度力、预应力、收缩徐变1 工程概况随着高等级公路和城市道路的迅速发展,立体交通的应用越来越多。
然而立体交通中的转向匝道桥,由于设计、活载、环境等多种因素作用,存在横向位移、扭转等病害。
这不仅影响了行车的舒适,而且给行车安全造成严重隐患。
本文选某桥梁转向匝道桥14#~18#墩预应力混凝土箱梁建立有限元模型。
该段桥梁上部结构为4跨(24.405+26.1+28+25)m一联的预应力连续箱梁,曲线半径为200m,且均为独柱墩。
14#、18#墩顶为双支座,支座为45×80×10.9cmF4型板式橡胶支座;其余独柱墩均为单支座,支座为GPZ9000sx×18盆式橡胶支座。
该段匝道桥上部结构为单箱双室预应力混凝土箱梁,梁内配以高强低松弛预应力钢绞线,锚具为OVM锚。
箱梁支点截面及跨中截面图见图1和图2。
图1 箱梁标准支点截面图(单位:cm)图2箱梁标准跨中截面图(单位:cm)2计算参数该桥主要计算参数如下:⑴预应力布置按全截面对称布置,采用Φ15.20mm预应力低松驰钢绞线,抗拉标准强度为fpk=1860MPa,弹性模量E=1.95×105MPa;⑵C50混凝土:重力密度γ=26.0kN/m3,弹性模量EC=3.45×104MPa;⑶沥青混凝土:重力密度γ=23.0kN/m3;⑷锚具:锚具变形、钢筋回缩按6mm(一端)计算;塑料波纹管摩阻系数μ=0.17,偏差系数k=0.0015;⑸均匀温升温降分别按20℃取值;竖向梯度温度效应:按《公路桥涵设计通用规范》(JTGD60-2004)规定取值。
旋转离心应力对弹性连接盘动力学特性的影响

转速对弹性连接盘固有频率和模态的影响模型参数:内直径32mm,外直径92mm,厚度1mm。
在求解旋转离心应力对弹性连接盘固有频率和模态影响的时候,要先求解出旋转离心应力,然后再进行模态分析。
具体步骤如下:1:利用 ANSYS 与CATIA 专用接口导入弹性连接盘实体模型。
2:定义材料属性杨氏模量E X = 2e5 ,泊松比PRXY=0.269。
材料密度:DENS=7.8e-6。
3:定义单元类型和划分网格。
采用自由网格划分方式,四面体单元Solid92。
图 4-4 网格划分后3 定义边界条件在定义边界条件以前,要先使求解过程包括预应力。
(1)从主菜单中选择Main Menu : Solution > Analysis Type > Sol’n Controls.打开Solution Controls 拾取窗口。
(2)在Basic 选项卡中激活Calculate prestress effects 选项,使求解过程包含预应力。
如下图所示,单击OK,关闭对话框。
图 4-5 选中预应力可用(3)从主菜单中选择Main Menu: Solution > Define Loads > Apply >Structural > Displacement > On Areas 命令,打开选择对话框,要求选择欲施加位移约束面。
(4)选择外圆面,打开Apply U,Rot On Nodes 对话框,如图4-6(5)选择All DOF,对所有节点此时施加了全约束。
(6)单击OK 按钮,Ansys 在选定节点上施加指定的位移约束。
4 施加转速惯性载荷(1)从主菜单中选择Main Menu: Solution > Define Load > Structural >Inertia > Angular Velocity > Global 命令,打开Apply Angular Velocity 对话框,如图4-7.图 4-7 转速的定义(2)在Global Cartesian Z-comp 文本框中输入52,需要注意的是,转速是相对于总体坐标系施加的,单位是rad/s.单击OK 按钮,施加转速引起的惯性载荷。
旋转预应力条件下的叶片流固耦合模态分析
(1. College of M echanical Electronical and Engineering, China University of M ining and Technology, Xuzhou J iangsu 221008, China;
在特定情况下进行模态分析 ,需要考虑预应力 效应 。比如在不可忽略的应力载荷作用下 ,对于某 一个或两个尺度上很薄的结构 ,结构的应力状态会 影响到它的固有频率 ,这一效应称为模态预应力效 应 。对于风机叶片 ,由于高速旋转会产生很大的旋 转预应力 , 加之流固耦合导致的不均匀气动力作
旋转预应力条件下的叶片流固耦合模态分析
摘 要 : 考虑了旋转预应力作用和流固耦合效应 ,对风机叶片系统进行动力学分析 。首先是在静态条件下进 行应力分析 ,获得预应力效应矩阵 ,并将外部载荷转化为结构的额外刚度 ,再建立在旋转预应力条件下流固耦合的 叶片系统动力学方程 。采用 ANSYS有限元软件和流体力学 Fluent软件 ,计算叶片系统的频率和模态并进行了分 析 。结果表明在旋转预应力与风机流场的流固耦合作用下 ,频率与模态有较为显著的改变 。
37
图 5 考虑旋转预应力与流固耦合作用后前 3阶的叶片叶片振型 Fig. 5 the three step s of blade modal under the rotation stress and coup ling2flow condition
扭曲方向与静态时的模态振型相反 。限于篇幅 ,无 法给出全部模态的叶片振型对比 ,但总的说来 ,模 态振型基本上都产生了最大位移位置点转移 ,位移 值减少及振动方向改变等上述的三种状况 。考虑 到模态频率的改变不大 (不超过 5% ) ,可以认为这 种变化是由旋转预应力与流固耦合作用而导致的 。 限于实验条件 ,无法对更加大型的风机进行分析 , 但基于上述模拟可推断 : 对于大型风机 ,其叶片更 加细长 ,受旋转预应力与流固耦合的影响会更为严 重 ,预应力效应会相对加剧 ,其模态改变程度将会 更大 。
旋转轮盘应力刚化效应对模态特性影响分析
旋转轮盘应力刚化效应对模态特性影响分析
苏荣华;王碧珺;丁文文;朱柳青
【期刊名称】《工程设计学报》
【年(卷),期】2009(016)004
【摘要】以ANSYS作为分析平台,对考虑应力刚化效应的旋转轮盘模态特性进行深入研究,揭示不同工作转速下旋转轮盘模态频率和振型变化规律.研究结果表明:当轮盘转速在一定范围内变化时,模态频率随着转速增加而增大,增加值与转速的平方成正比.在此基础上,引入频率影响系数的概念,提出了计算动模态频率的简化公式,并给出了适用范围.研究表明,在一定条件下,随着转速的提高,旋转轮盘的第1阶振型就可能发生变化.
【总页数】6页(P292-296,307)
【作者】苏荣华;王碧珺;丁文文;朱柳青
【作者单位】辽宁工程技术大学力学与工程学院,辽宁,阜新,123000;辽宁工程技术大学力学与工程学院,辽宁,阜新,123000;辽宁工程技术大学力学与工程学院,辽宁,阜新,123000;辽宁工程技术大学力学与工程学院,辽宁,阜新,123000
【正文语种】中文
【中图分类】TB122
【相关文献】
1.计算汽轮机轮盘旋转应力的传递矩阵法 [J], 王燮山;刘宗德
2.考虑应力刚化影响的风力机叶片振动模态分析 [J], 孙保苍;李鹏飞
3.转子、轮盘和叶片系统的应力分析——旋转对称结构应力分析方法 [J], 周传月;邹经湘;闻雪友;盛惠渝
4.考虑离心刚化效应的旋转风力机叶片动力特性分析 [J], 陈小波;李静;陈健云
5.应力刚化及流体压缩性对混流式水轮机叶片动力特性的影响分析 [J], 陈香林;张立翔;闫华
因版权原因,仅展示原文概要,查看原文内容请购买。
毕业设计(论文)-预应力对高速旋转轮盘模态的影响分析[管理资料]
1 绪论问题的提出轮盘是发动机的重要零件之一,,转速高,其工作条件十分恶劣,设计要求高、,由于结构要求,大部分轮盘都开有中心孔或其它通气孔,还开有榫槽以便于与叶片联接,、轴向还有较大的温差,承受很大的热应力,,造成重大故障,其原因是轮盘产生了一阶伞型振动的共振,,轮盘结构日趋轻型化,轮盘做得很薄。
因此在高负荷、长寿命的工作情况下,轮盘因振动疲劳而断裂的故障有所增多。
旋转轮盘在高速旋转状态下会表现出与低速或非旋转状态下迥异的力学性能。
许多转子机械受刚度特性和非保守效应的阻尼特性的影响,其运转工况下的动态性能与静止时相比有很大的差异。
在进行高速旋转机械的转子系统动力设计时,需要对转动部件进行模态分析,求解出其固有频率和相应的模态振型。
通过合理的设计使其工作转速尽量远离转子系统的固有频率以避免由于共振而产生开裂破坏。
而对于高速部件,工作时由于受到离心力的影响,其固有频率跟静止时相比会有一定的变化。
为此,在进行模态分析时需要考虑离心力引起的预应力的影响。
如果忽略了预应力的影响就会使原有的系统遭到破坏,降低系统的稳定性和可靠性。
因此掌握高速旋转轮盘运转工况各种转速下的动力特性,对于了解不平衡振动响应以及可能出现的不稳定性等均有实际意义。
国内外研究现状轮盘是旋转机械中的常见部件,如水泵叶轮、风机叶轮轮盘、汽轮机转子上的轮盘等,它的强度、振动是设计、加工中重点考虑的问题之一。
由于轮盘结构复杂, 因此,在利用有限元分析计算时,建模是很重要的一个环节。
文献[1]采用在UG上进行几何建模,运用NASTRAN建立有限元模型,对轮盘进行静强度分析和模态分析。
for (。
它可以在windows95或windowsNT下运行。
、模态、屈曲、热传导、动力学、非线性和设计优化等各种类型分析。
,根据不同的几何模型提供了多种不同的生成和定义有限元模型工具,包括:网格划分、边界和载荷定义。
预应力技术能在不增加零件尺寸及材料性能的前提下,提高其承载能力,使用性能及工作寿命。
螺栓及其预紧力对大型转盘轴承接触载荷分布的影响
兰
二 Z 轴承 2016年1期
CN41 — 1148/TH Bearing 2016 ,No.1
..I试 验 与 分 析
螺 栓 及 其 预 紧 力对 大 型 转 盘 轴 承 接 触 载 荷 分布 的影 响
王存 珠 ,陈观 慈,李 肖杰 ,温戈
(昆明理S-大学 机 电S-程学院,昆明 650500)
王存珠 ,等 :螺 栓及 其预紧力对大型转盘轴承接触载荷分 布的影响外 学 者 对 大 型 转 盘 轴 承 力 学 性 能 做 了诸 多研 究 。文 献 [5]不 考 虑 轴 承 支 承 结 构 和 套 圈变 形 ,建 立 了 双排 四点 接 触 球 转 盘 轴 承 的 载 荷 分布 与接 触 角 分 布 模 型 ,讨 论 了轴 承 几 何 参 数 对 轴承 承载 能 力 的影 响 ,为更 好 地 选 择 和 设 计 双 排 四点接触球转盘轴承提供 了依据。文献 [6]采 用 非线性 弹簧 模 拟 钢 球 一沟道 接 触 ,在 螺 栓 与构 件 接触 区施 加 等 效 均 匀 压 力 模 拟 螺 栓 预 紧力 ,对 转 盘轴 承 的有 限元 模 型 进 行 了 简 化 ,通 过 理 论 和 经 验公 式验 证 了该 模 型 的正 确 性 ,并 且 利 用 此 模 型分 析 了螺 栓 预 紧 力 对 转 盘 轴 承 载 荷 分 布 的影 响 。文献 [7]利 用 ANSYS Workbench软 件对 变 桨 轴 承进行 了三 维 建 模 ,并 对 其 进 行 了静 态 接 触 力
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 绪论问题的提出轮盘是发动机的重要零件之一,,转速高,其工作条件十分恶劣,设计要求高、,由于结构要求,大部分轮盘都开有中心孔或其它通气孔,还开有榫槽以便于与叶片联接,、轴向还有较大的温差,承受很大的热应力,,造成重大故障,其原因是轮盘产生了一阶伞型振动的共振,,轮盘结构日趋轻型化,轮盘做得很薄。
因此在高负荷、长寿命的工作情况下,轮盘因振动疲劳而断裂的故障有所增多。
旋转轮盘在高速旋转状态下会表现出与低速或非旋转状态下迥异的力学性能。
许多转子机械受刚度特性和非保守效应的阻尼特性的影响,其运转工况下的动态性能与静止时相比有很大的差异。
在进行高速旋转机械的转子系统动力设计时,需要对转动部件进行模态分析,求解出其固有频率和相应的模态振型。
通过合理的设计使其工作转速尽量远离转子系统的固有频率以避免由于共振而产生开裂破坏。
而对于高速部件,工作时由于受到离心力的影响,其固有频率跟静止时相比会有一定的变化。
为此,在进行模态分析时需要考虑离心力引起的预应力的影响。
如果忽略了预应力的影响就会使原有的系统遭到破坏,降低系统的稳定性和可靠性。
因此掌握高速旋转轮盘运转工况各种转速下的动力特性,对于了解不平衡振动响应以及可能出现的不稳定性等均有实际意义。
国内外研究现状轮盘是旋转机械中的常见部件,如水泵叶轮、风机叶轮轮盘、汽轮机转子上的轮盘等,它的强度、振动是设计、加工中重点考虑的问题之一。
由于轮盘结构复杂, 因此,在利用有限元分析计算时,建模是很重要的一个环节。
文献[1]采用在UG上进行几何建模,运用NASTRAN建立有限元模型,对轮盘进行静强度分析和模态分析。
for (。
它可以在windows95或windowsNT下运行。
、模态、屈曲、热传导、动力学、非线性和设计优化等各种类型分析。
,根据不同的几何模型提供了多种不同的生成和定义有限元模型工具,包括:网格划分、边界和载荷定义。
预应力技术能在不增加零件尺寸及材料性能的前提下,提高其承载能力,使用性能及工作寿命。
它是使零件在承受工作载荷之前被施加一定的反向预应力,当其承受工作载荷时,工作应力与预应力叠减,从而使零件的实际应力得以减小,承载能力提高,变形量减小,寿命延长。
对于以离心力为其主要工作荷载的高速旋转零件。
如离心压缩叶机,高速泵叶轮,高速旋转刀具等,也可以通过预应力处理来提高其承载能力,延长寿命。
文献[2]从基本理论出发,对该类零件在一定转速下的动态固有频率作三维有限元分析。
经过理论分析和实例证明,由于离心力的影响,旋转轮盘低阶模态的动态固有频率增加较大。
另外,轮盘的厚度越薄,转速越高,其影响也越大。
文献[3]采用激光全息干涉法对某型发动机一级压气机盘进行振动试验研究,在0~15 000Hz频率范围内获得了7个振动模态的静频及振型,并根据试验结果研究该轮盘的行波振动,分析轮盘的共振特性及临界转速。
文献[4]用有限元等数值分析的方法,探讨了叶片动力刚化对其振动特性的影响。
利用国际流行的有限元分析软件ANSYS,对某型压气机的盘鼓在工作过程中的应力状态以及振动模态进行了仿真计算。
文献[5]针对600MW汽轮发电机组低压转子-轴承系统,建立了整轴模型和低压转子模型,采用有限元分析软件ANSYS进行模态分析时提出使用Lagrange乘子法来处理约束方程,计算汽轮机转子的固有频率和临界转速,从而避免工作转速达到临界转速产生共振现象,最后通过临界转速和振型图分析了低压转子的特性。
文献[6]简述了通过预应力提高旋转零件承载能力与寿命的基本原理,给出了最低及最高两个极限试验转速,并对试验设备的技术性能提出要求。
随着制造水平的提高以及对新型轴承结构的理论探索,外存储器正朝着超大容量、,盘片的厚度越来越薄,因此,盘/轴系统高速旋转时,盘片的弹性变形主要源于旋转时的轴对称膜应力-离心力,,并给出了部分振动模态图.文献[7]研究给出了盘/轴系统高速旋转时盘片振动模态的计算方法,并开发了振动模态的仿真程序,给出了部分仿真结果.文献[8]中以磁悬浮轴承转子系统的组成及工作原理为基础,在ANSYS9. 0中建立了磁悬浮转子的三维有限元模型。
采用Subspace法计算了前4阶固有频率和振型,并与试验模态分析结果进行了对比。
结果显示,基于有限元法得到的数据与试验模态分析基本一致,所建立的有限元模型为柔性转子系统设计提供了一定的理论依据。
文献[9]建立了叶片-轮盘耦合系统振动固有特性计算分析模型,利用有限元通用程序NASTARN的循环对称分析功能和几何非线性分析功能,对某舰用燃气轮机叶片-轮盘结构进行计算分析。
计算中考虑了旋转离心力及材料参数随温度变化对固有特性的影响,得到的谐波共振频率与实测结果基本吻合。
本文的主要工作旋转轮盘是许多机械装置最基本的也是最重要的零件之一。
轮盘在高速旋转状态下由于离心力的影响,其固有频率与静止时相比也会发生一定的变化,因此在对轮盘进行模态分析不可忽略预应力的影响。
本文主要做了以下工作:1)本文首先介绍了有限元法以及ANSYS软件,建立了高速旋转轮盘的有限元模型。
2)介绍静力学分析基本理论,分析了轮盘在相对稳定的离心力载荷的作用下的静应力及位移的问题。
3)在此静应力分析的基础上,基于旋转体动力学方程,略去初位移刚度矩阵,建立了轮盘的有限元形式动力学方程。
并基于此方程作了模态分析,详细分析轮盘在旋转时的振动特性。
利用ANSYS软件,直接求出轮盘在静止状态和不同旋转速度状态下整体结构的固有频率、振型,并给出振型的彩色云图和动画显示;通过对固有频率、振型的分析得出预应力对高速旋转轮盘模态的影响规律。
2 高速旋转轮盘模态分析基本理论与方法在实际工作中,轮盘经常要受到随时间变化的动载荷的作用。
当所受的动载荷较大时,或者虽然不大,当作用力的频率与轮盘的某一阶固有频率接近时, 轮盘将产生强烈的共振,从而引起很高的动应力, 造成轮盘强度破坏或变形。
因此, 有必要对轮盘作动力学模态分析, 也就是要分析轮盘的固有频率、主振型, 以及在动载荷作用下的动挠度、动应力等等。
模态分析概述模态分析的定义一般地,以振动理论为基础、以模态参数为目的的分析方法,称为模态分析。
更确切地说,模态分析是研究系统物理参数模型、模态参数模型和非参数模型的关系,并通过一定手段确定这些系统模型理论及其应用的一门学科[10]。
通过模态分析得到的结果,可以帮助结构设计者设计合理结构以避开共振频率。
模态分析的实质是一种坐标变换。
其目的在于把原在物理坐标系统中描述的响应向量,放到所谓“模态坐标系统”中描述。
这一坐标系统的每一个基向量恰是振动系统的一个特征向量。
运用这一坐标系统的好处是:利用各特征向量之间的正交特性,可使描述响应向量的各个坐标均可单独求解。
换句话说,在这一坐标系统下,振动方程是一组互无耦合的方程,每一个坐标均可单独求解。
根据研究模态分析的手段和方法的不同,模态分析分为理论模态分析和实验模态分析两种。
理论模态分析是指以线性振动理论为基础,研究激励、系统和响应三者的关系;实验模态分析又称模态分析的实验过程,是解析模态分析的逆过程。
计算模态分析实际上是一种理论建模过程,主要是运用有限元法对振动结构进行离散,建立系统特征值问题的数学模型,用各种近似方法求解系统特征值和特征向量。
模态分析在工程中的应用1)模态分析在结构性能评价中的直接应用根据模态分析的结果,即模态频率、模态振型、模态阻尼等模态参数,对被测结构进行直接的动态性能评估。
对一般结构,要求各阶模态频率远离工作频率,或工作频率不落在某阶模态的半功率带宽内;对结构贡献较大的振型,应使其不影响结构正常工作为最佳。
这是模态分析的直接应用,已成为工程界的基本方法。
2)模态分析在结构动态设计中的应用以模态分析为基础的结构动态设计,是近年来振动工程界开展的最广泛的研究领域之一。
传统的结构设计是以经验和反复实测为主要手段。
因为尽管依据模态分析结果和响应实验容易判断出初步结构的性能缺陷,但在结构修改问题上却往往茫然无所知,设计工程师只能依据经验和现有条件进行反复修改和实测,有时甚至将原设计完全推翻重新设计。
这样就大大减缓了设计速度,设计质量也难以达到最优。
3)模态分析在故障诊断和状态检测中的应用利用模态分析得到的模态参数等结果进行故障判别,日益成为一种有效而实用的故障诊断和安全检验方法。
如根据模态频率的变化判断裂纹的出现,根据振型的分析判断裂纹的位置,根据转子支撑系统阻尼的改变判断和预报转子的失稳。
4)模态分析在声控中的应用声音控制包括利用振动和抑制振动两个方面。
抑制结构的辐射噪声,在很多问题中都很突出。
模态分析为分析噪声产生的原因及治理提供了有效的方法。
高速旋转轮盘模态分析的基本理论固有频率根据达朗贝尔原理, 只要在研究对象所受的外力中加入惯性力, 就可以像建立静力学平衡方程那样去建立动力学方程[11]。
一个多自由度系统有阻尼振动方程如下:[]M {}x +[]C {}x +[]K {}x ={})(t P (2-1)式中 []M :系统质量矩[]C :系统阻尼矩阵[]K :系统刚度矩阵{}x :广义坐标的列阵{}x:代表广义速度 {}x :代表广义加速度{})(t P :所受外部载荷因为结构的固有频率和振型与所受外力{})(t P 无关, 而小阻尼对固有频率和振型影响并不大。
因此常用无阻尼自由度振动方程求结构的频率和振型, 即上式简化为下式:[]M {}x +[]K {}x =0 (2-2)由于弹性体的自由振动总可以分解为一系列的简谐振动的叠加。
因此可设其特解为 )sin(θω+=t A x j j (j =1,2,…,n ) (2-3) 此特解表示系统内各个坐标偏离平衡值时均以同一频率ω和同一初相角θ作不同振幅的简谐运动。
上式也可以写作矩阵形式:{}{})sin(θω+=t A x (2-4)其中j A A =为各坐标振幅组成的n 阶列阵。
将上式代入方程(2-2),化作矩阵K 和M 的广义本征值问题([]K -2ω[]M ){}A =0 (2-5){}A 有非零解的的充分与必要条件为系数行列式等于零[][]02=-M K ω (2-6)展开后得到2ω的n 次代数方程,即系统的本征方程22(1)2110n n n n a a a ωωω--++++= (2-7)对于平衡状态稳定的正定系统,各坐标只能在平衡位置附近作微幅简谐振动。
方程(2-7)存在2ω的n 个正实根,即系统的本征值。
每个本征值所对应的i ω(1,2,,)i n =为系统的n 个固有频率,将其由小到大按顺序排列为321ωωω<<…n ω< (2-8)因此本征方程(2-7)也可称作频率方程。
与单自由度系统相同,多自由度系统的固有频率也是由系统本身的物理参数所决定,与起始运动状态无关。
