拐点的判定条件
高数上凹向、拐点、作图

2 y 36 x 24 x 36 x x 3 2 2 0 3 得 x 0 , x 令y 0 1 2 · · 3 x 0时, y 0; 在区间(-∞,0]内曲线是凹的。 2 2 0 x 时, y 0 ; 在区间[0, ]上曲线是凸的。 3 3 2 x 时, y 0. 在区间[ 2 ,+∞)内曲线是凹的。 3 3 2 11 0 , 1、 , 是拐点. 3 27
x2 2
得到曲线上的两个点 (0 ,
1 2
)、( 1,
1
另外f 2
1 , 2 2 e
1
加辅助点 ( 2 ,
2e 1 ). 2 2 e
)
1
2
注:本例特点 (1)利用函数的奇偶性; (2)补充点(0 ,y ( 0 ) ),(2 ,y ( 2 ) ); (3)有水平渐近线。
f ' ( x1 ) f ' ( x2 ) f ' ( x3 ),
f x 递减
f x 0
f x 0
在有些教材中,凹的(曲线)又叫“上凹”,凸的又叫“下凹”。
连续曲线上,不同凹向曲线段的分界点,称为曲线的拐点。 注意:拐点是曲线上的点,应由两个坐标表示:( x0 , f ( x0 ) ). 前面讲过的极值点,是取得极值时自变量的值,记 为 x = xi。 两者不同。 2、曲线凹向的判定 P106定理3.8 函数y = f ( x ) 在闭区间 [ a , b ] 上连续,在开区间内二阶可导, 则当 仍可用“雨水法则” f ”( x ) > 0 时,曲线上凹(凹); 帮助记忆 f ”( x ) < 0 时,曲线下凹(凸)。
曲线的凹向与拐点
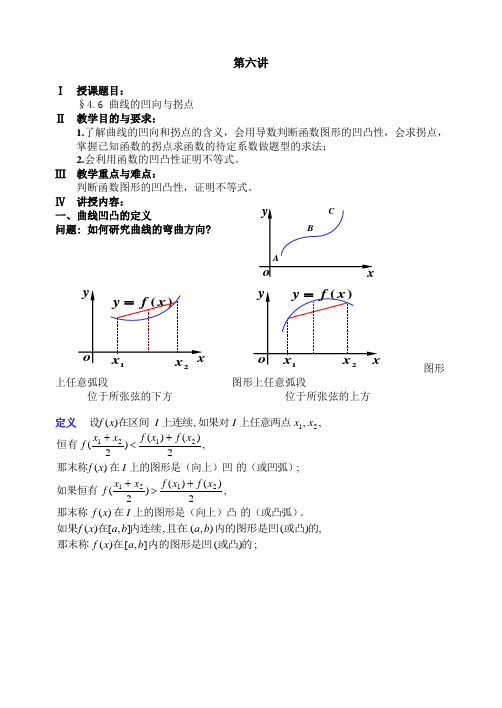
第六讲Ⅰ 授课题目:§4.6 曲线的凹向与拐点 Ⅱ 教学目的与要求:1.了解曲线的凹向和拐点的含义,会用导数判断函数图形的凹凸性,会求拐点, 掌握已知函数的拐点求函数的待定系数做题型的求法;2.会利用函数的凹凸性证明不等式。
Ⅲ 教学重点与难点:判断函数图形的凹凸性,证明不等式。
Ⅳ 讲授内容:一、曲线凹凸的定义问题: 如何研究曲线的弯曲方向?图形上任意弧段 图形上任意弧段位于所张弦的下方 位于所张弦的上方定义,,,)(21x x I I x f 上任意两点如果对上连续在区间设.的(或凸弧)上的图形是(向上)凸在那末称如果恒有的(或凹弧)上的图形是(向上)凹在那末称恒有I x f x f x f x x f I x f x f x f x x f )(,2)()()2(;)(,2)()()2(21212121+>++<+;)(],[)(,)(),(,],[)(的或凸内的图形是凹在那末称的或凸内的图形是凹且在内连续在如果b a x f b a b a x f二、曲线凹凸的判定递增)(x f '0>''y 递减)(x f '0<''y定理 内若在内具有一阶和二阶导数在上连续在如果),(,),(,],[)(b a b a b a x f .],[)(,0)()2(;],[)(,0)()1(上的图形是凸的在则上的图形是凹的在则b a x f x f b a x f x f <''>''例1 .3的凹凸性判断曲线x y =解 ,32x y ='Θ,6x y =''时,当0<x ,0<''y 为凸的;在曲线]0,(-∞∴ 时,当0>x ,0>''y 为凹的;在曲线),0[+∞∴ 注意到,.)0,0(点是曲线由凸变凹的分界点 二、 曲线的拐点及其求法1、定义 连续曲线上凹凸的分界点称为曲线的拐点. 注意:拐点处的切线必在拐点处穿过曲线.2、拐点的求法定理 如果)(x f 在),(00δδ+-x x 内存在二阶导 数,则点())(,00x f x 是拐点的必要条件是0)(0"=x f . ,))(,(00是拐点又x f x Θ,])([)(0两边变号在则x x f x f ''='',)(0取得极值在x x f '∴,条件由可导函数取得极值的 .0)(=''∴x f方法1: ,0)(,)(00=''x f x x f 且的邻域内二阶可导在设函数 ;))(,(,)()1(000即为拐点点变号两近旁x f x x f x '' .))(,(,)()2(000不是拐点点不变号两近旁x f x x f x '' 例2 .14334的拐点及凹、凸的区间求曲线+-=x x y 解 ),(:+∞-∞D Θ,121223x x y -=').32(36-=''x x y,0=''y 令.32,021==x x 得x(),0-∞20,3⎛⎫ ⎪⎝⎭ 23 2,3⎛⎫+∞ ⎪⎝⎭abxy o )(x f y =BAabABxyo )(x f y =()f x '' + 0 -0 + ()f x凹的拐点)1,0(凸的拐点 )2711,32( 凹的).,32[],32,0[],0,(+∞-∞凹凸区间为 方法2:.)())(,(,0)(,0)(,)(00000的拐点是曲线那末而且的邻域内三阶可导在设函数x f y x f x x f x f x x f =≠'''=''例3 .)]2,0([cos sin 的拐点内求曲线πx x y += 解 ,sin cos x x y -=',cos sin x x y --=''.sin cos x x y +-=''',0=''y 令.47,4321ππ==x x 得2)43(='''πf ,0≠2)47(-='''πf ,0≠内曲线有拐点为在]2,0[π∴).0,47(),0,43(ππ注意 .)())(,(,)(000的拐点也可能是连续曲线点不存在若x f y x f x x f =''例4 .3的拐点求曲线x y =解 ,0时当≠x ,3132-='x y ,9435--=''x y.,,0均不存在是不可导点y y x '''=,0,)0,(>''-∞y 内但在;]0,(上是凹的曲线在-∞ ,0,),0(<''+∞y 内在.),0[上是凸的曲线在+∞.)0,0(3的拐点是曲线点x y =∴Ⅴ 小结与提问:小结:1.曲线的弯曲方向——凹凸性;2.凹凸性的判定.3.改变弯曲方向的点——拐点;4.拐点的求法1, 2.思考题:设)(x f 在),(b a 内二阶可导,且0)(0=''x f ,其中),(0b a x ∈,则,(0x ))(0x f 是否一定为曲线)(x f 的拐点?举例说明. 思考题解答:因为0)(0=''x f 只是,(0x ))(0x f 为拐点的必要条件, 故,(0x ))(0x f 不一定是拐点. 例 4)(x x f =),(+∞-∞∈x 0)0(=''f 但)0,0(并不是曲线)(x f 的拐点.Ⅵ 课外作业:练 习 题 一、填空题:1、 若函数)(x f y =在(b a ,)可导,则曲线)(x f 在(b a ,)内取凹的充要条件是____________.2、 曲线上____________的点,称作曲线的拐点 .3、 曲线)1ln(2x y +=的拐点为__________.4、 曲线)1ln(x y +=拐点为_______. 二、求曲线x e y arctan =的拐点及凹凸区间 . 三、利用函数图形的凹凸性,证明不等式: 22y x yx ee e +>+ )(y x ≠.四、求曲线⎩⎨⎧==θθ2sin 2cot 2a y a x 的拐点 . 五、试证明曲线112+-=x x y 有三个拐点位于同一直线上 .六、问a 及b 为何值时,点(1,3)为曲线23bx ax y +=的拐点? 七、试决定22)3(-=x k y 中k 的值,使曲线的拐点处的法线通过原点 . 练习题答案一、1.),()(b a x f 在'内递增或0)(),,(>''∈x f b a x ; 2.凹凸部分的分界点;3.]2,(),,2[),2,2(2-∞+∞e; 4.)2ln ,1(),2ln ,1(-.二、拐点),21(21arctan e ,在]21,(-∞内是凹的, 在),21[+∞内是凸的.四、拐点)23,332(a a 及)23,332(a a -.五、).)32(431,32(),)32(431,32(),1,1(+++-----六、2,2=-=b a .七、 82±=k。
函数凸凹性与拐点关于

§5函数的凸性与拐点教学目的与要求:掌握凸函数凹函数的定义掌握可导函数为凸函数的充要条件掌握拐点的定义掌握判断函数拐点的必要条件和充分条件教学重点,难点:可导函数为凸函数的充要条件拐点的判别方法教学内容:作函数的图形时,仅知道函数单调性是不够的,还应知道其曲线弯曲的情形,即曲线凹凸的概念, 读者已经熟悉函数2)(x x f =和x x f =)(的图象。
它们不同的特点是:曲线2x y =上任意两点间的弧段总在这两点连线的下方;而曲线x y =则相反,任意两点间的弧段总在这两点连线的上方,我们把具有前一种特性的曲线称为凸的,相应的函数称为凸函数:后一种曲线称为凹的,相应的函数称为凹函数。
定义1 设f 为定义在区间I 上的函数,若对I 上的任意两点21,x x 和任意实数)1,0(∈λ总有),()1()())1((2121x f x f x x f λλλλ-+≤-+ (1)则称f 为I 上的凸函数. 反之,如果总有),()1()())1((2121x f x f x x f λλλλ-+≥-+ (2) 则称f 为I 上的凹函数。
如果(1)、(2)中的不等式改为严格不等式,则相应的函数称为严格凸函数和严格凹函数。
图6-12中的(a )和(b)分别是凸函数和凹函数的几何形状,其中B AC x f B x f A x x x )1(),(),(,)1(2121λλλλ-+===-+=。
容易证明:若f -为区间I 上的凸函数,则f 为区间I 上的凹函数,因此今后只需讨论凸函数的性质即可。
引理 f 为I 上的凸函数的充要条件是:对于I 上的任意三点321x x x <<,总有 23231212)()()()(x x x f x f x x x f x f --≤-- (3) (析) 必要性 要证(3)式成立, 需证)()()()()()(123212223x f x x x f x x x f x x -≤-+-)()(312x f x x -+即. ),()()()()()(312123213x f x x x f x x x f x x -+-≤- 记1323x x x x --=λ,则312)1(x x x λλ-+=,由f 的凸性易知上式成立.充分性 在I 上任取两点),(,3131x x x x <在],[31x x 上任取一点)1(12λλ-+=x x ·),1,0(,3∈λx 即1323x x x x --=λ,由必要性的推导逆过程,可证得 )())1((131x f x x f λλλ≤-+)()1(3x f λ-+,故f 为I 上的凸函数。
函数的凹凸性与拐点的定义与求法

f ′′( x0 ) = 0, 而 f ′′′( x0 ) ≠ 0 , 那末 ( x0 , f ( x0 )) 是曲 线 y = f ( x ) 的拐点.
例3 求曲线 y = sin x + cos x ([0,2π ]内) 的拐点. 解 y′ = cos x − sin x , y′′ = − sin x − cos x ,
注意:拐点处的切线必在拐点处穿过曲线 注意 拐点处的切线必在拐点处穿过曲线. 拐点处的切线必在拐点处穿过曲线 2.拐点的求法 2.拐点的求法
( 理2 定 2 如 f (x)在 x0 − δ , x0 + δ )内 在 阶 理 果 存 二 导
( x0 , f ( x0 ))是拐点的必要条件是f "( x0 ) = 0. 数则 , 点
一、曲线凹凸的定义
问题:如何研究曲线的弯曲方向 问题 如何研究曲线的弯曲方向? 如何研究曲线的弯曲方向
y
C
B
A
o
x
y
y = f (x)
y
y = f (x)
o
x1
x2 x
o
x1
x2
x
图形上任意弧段位 于所张弦的下方
图形上任意弧段位 于所张弦的上方
( 定义 设f ( x)在 a, b)内连续, 如果对(a, b)内任意 x1 + x2 f ( x1 ) + f ( x2 ) )< , 两点x1, x2 , 恒有 f ( 2 2 ( 那末称 f ( x)在 a, b)内的图形是凹的; 如果对 a, b)内任意两点 x1, x2 , 恒有 ( x1 + x2 f ( x1 ) + f ( x2 ) f( )> , 2 2 ( 那末称 f ( x)在 a, b)内的图形是凸的;
函数的极值与拐点

函数的极值与拐点函数在数学中扮演着重要的角色,它描述了数学中数量间的关系。
其中,函数的极值和拐点是函数的重要特征,它们提供了函数图像的关键信息。
在本文中,我们将详细讨论函数的极值和拐点,并解释它们的定义、性质和应用。
一、极值极值是函数在特定区间内取得的最大值和最小值。
对于函数f(x),如果存在一个实数x0,使得在x0的某个邻域内,f(x)的值不超过(或不低于)f(x0),那么称f(x0)为函数f(x)的极大值(或极小值)。
极大值和极小值统称为极值。
1.1 极大值和极小值的判定首先,我们需要了解一些判定极大值和极小值的条件。
设f(x)在区间I的内部可导,且在I的端点(若存在)或无穷远处的极限存在(有限或无穷),则:- 若f'(x)在I的内部从正数变为负数,则f(x)在该点取得极大值。
- 若f'(x)在I的内部从负数变为正数,则f(x)在该点取得极小值。
- 若f'(x)在I的内部不变号,则f(x)在该点不取得极值。
1.2 求解极值的方法求解函数的极值是一个重要的问题。
对于一般的函数,我们可以通过以下步骤来求解极值:1)求函数f(x)的导函数f'(x);2)求解方程f'(x)=0,找到导函数的驻点;3)根据判定条件,确定驻点是否为极值点;4)将所有的驻点和区间端点的函数值进行比较,找到函数的极值。
二、拐点拐点是函数图像中出现曲线凹凸性改变的点,也称为拐点。
在拐点处,函数的二阶导数发生变化。
通过分析函数的拐点可以帮助我们了解函数曲线的特征。
2.1 拐点的定义与判定设函数f(x)在区间I上可导,若存在实数x0,使得f''(x0)=0,且f''(x)在x0的邻域内两侧的导数符号相反,那么称x0为函数f(x)的拐点。
2.2 求解拐点的方法求解函数的拐点也是一个关键问题。
一般来说,我们可以通过以下步骤来求解拐点:1)求函数f(x)的二阶导函数f''(x);2)解方程f''(x)=0,找到二阶导函数的零点;3)根据判定条件,确定零点是否为拐点。
论曲线的拐点

注 :二阶导数不存在 的点和二阶 导数等于零的点不一定是拐点. 3 拐点的充分条件 命题 1 设 Y= x 在 U(o 内连续 ,在 。 o 内二阶可导 ,在 j 可 导或 /(o =∞ ,则有 : f() x) () X c 0 ) X 1 )若在 。 和 。X) f () ( ) (o 内 的符号相反 ,则 (of X) 是曲线 Y=f x 的拐点. x, (o) () 2若在 。 和 。X) ) ( ) (o 内f () 的符号相 同,则 (of X)不是 曲线 Y=f x 的拐点. X, (o) () 命题 2 若 Y=f x 在某 U(o ) () x, 内二阶可导且 厂 (o =0,三 阶单侧导数 ) X 1 )若 ) , ) 同号 ,则点 (of X)是 曲线 Y=f x 的拐点 . x, (o) () ) , j) c 存在 ,则有 : 0
() 0;当 . X,o ) / () < ] oX 十 时 >0.从而点 (of X)是 曲线 Y=f x 的拐点 . c ∈( X , (o) ()
收稿 日期 :20-92 0 90 .8
基 金项 目:衡水 学院科 研基 金 资助课题 (094 ) 200 9
作 者简 介 :孙兰敏 (9 3) 女, 16一 , 河北 深州 人, 衡水 学 院数学 与计 算机 学院 教授
f A l 1 ) > ( + 1 A f x ) ( x+(_ ) 厂 ) (一 ) (2 ,则称 ,() 区间 ,上 的严格 下凹 函数 ,也称 曲线 Y= 是 严格下 是 ()
凹 曲线.
定义 3 设 曲线 =f x 在点 (of X)处有穿过 曲线的切线 ,且在切点近旁 ,曲线在切线 的两侧分别 Ⅲ () X , (o) 是严格下 凸和严格下凹 的,这时称点 (of X)是 曲线 Y=f x 的拐点 . X, (o) () 由定义可见拐点是 曲线下凸部分和 下凹部分 的分界点 .
曲线的凹凸性和拐点
9节曲窝族畝拐点 I 忖一曲线百四的定义/H\ \二曲线凹凸:的判定「、三曲线的驾蛙姜护-一、曲线凹凸的定义如何研究曲线的弯曲方向?位于所张弦的下方问题图形上任意弧段位于所张弦的上方上—页卞一页返叵定义设/'(X)在(sZ>)内连续,如果对S上)内任意两点r严“恒2 2 那末称/(乂)在(6巧内的图形是凹的;如果恒有八巴上2)>八&)+八兀2)2那末称/(X)在@,巧内的图形是凸的。
上—页下—夷E?凹弧:曲线上任意一点切线都在曲线弧的下方。
凸弧:曲线上任意一点切线都在曲线弧的上方。
上—页下—夷I& E?曲线凹凸的判定X, +X,3畐eg __ ),2, ,X, +X, ―X. +X, — X,/(")-/(— )=广(刍)(兀- ')=厂(£)— -2 2 2X, +X.3^2 €( " 2 ),2X, +x\ X,十*. X, -X.定理1如果/•(*)在0上]上连续,在("0)内具有二阶导数,若在仗上)内(1)/"(x)>0,则八工)在|«,A1上的图形是凹的,(2)/^7x)<0,则八丄)在B上]上的图形是凸的。
上—页下—页证明:(1)分析:即证任取两点兀]宀(" < 兀2)要证八2 — 2X, + X予X. + X.————)1 >«2 2—X上—页下—页返叵/(©)-/(—)=厂©)(*2---—2 厂©)—-2 2 2上—页下页逅叵上—页 下—页 返叵两式相加为:X, X- + 七 X, —X, 1/(和-/( ~)]+[/(©)-[/烷)-/("】 ~-2 22即证;厂(务)一厂(£)>o V V 务)事实上:(冬一気)同理可证明(2)上—页.•・曲线在【U,y >)为凹的; 而 厂(G>0 ••・/'(§) 一厂(G>0(纟 <塩)例1判断曲线y = 的凹凸性解.•・• = 3厂,y" = 6x,当XV 0时,y"vO,・•・曲线在(-00,0]为凸的当x>0时,y">0,注意,点(0,0)是曲线由凸变凹的分界点。
高等数学第6章第5节函数的凹凸性个与拐点

§5.函数的凹凸性个与拐点引言上面已经讨论了函数的升降与极值,这对函数性状的了解是有很大作用的.为了更深入和较精确地掌握函数的性状,我们在这里再讲述一下有关函数凸性的概念及其与函数二阶导数的关系.什么叫函数的凸性呢?我们先以两个具体函数为例,从直观上看一看何谓函数的凸性.如函数y 所表示的曲线是向上凸的,而2y x =所表示的曲线是向下凸的,这与我们日常习惯上的称呼是相类似的.或更准确地说:从几何上看,若y =f(x)的图形在区间I 上是凸的,那么连接曲线上任意两点所得的弦在曲线的上方;若y =f(x)的图形在区间I 上是凹的,那么连接曲线上任意两点所得的弦在曲线的下方.如何把此直观的想法用数量关系表示出来呢?在曲线上任取两点A 、B ,设其坐标分别为11(,())x f x 、22(,())x f x ,弦AB 在曲线上方⇔12(,)x x x ∀∈,有211121()()()()()f x f x f x f x x x x x -≤+--,可简化为(0,1)λ∀∈,12,x x I ∀∈都有1212((1))()(1)()f x x f x f x λλλλ+-≤+-,从而有以下定义:一、 凸(凹)函数的定义及判定1 凸(凹)函数的定义定义1 设函数f 为定义在区间I 上的函数,若对I 上任意两点1x 、2x 和任意实数(0,1)λ∈总有1212((1))()(1)()f x x f x f x λλλλ+-≤+-,则称f 为I 上的凸函数.反之,如果总有1212((1))()(1)()f x x f x f x λλλλ+-≥+-,则称f 为I 上的凹函数.注 易证:若一f 为区间I 上的凸函数,则f 为区间I 上的凹函数,因此,今后只讨论凸函数的性质即可.2、凸函数的判定1引理 f 为I 上的凸函数⇔对于I 上任意三点123x x x <<总有:32212132()()()()f x f x f x f x x x x x --≤-- 注 同理可证:有上任意三点对上的凸函数为,321x x x I I f <<⇔232313131212)()()()()()(x x x f x f x x x f x f x x x f x f --≤--≤-- (4) 如果f 是I 上的可导函数,则进一步有:2 定理6.13(可导函数为凸函数的等价命题) 设f 为区间I 上的可导函数,则下述论断互相等价:(1)f 为I 上的凸函数;(2)f '为I 上的增函数;(3)对I 上的任意两点12,x x 总有21121()()()()f x f x f x x x '≥+-如果f 在I 上二阶可导,则进一步有:3定理6.14(凸函数与二阶导数的关系) 设f 为I 上的二阶可导函数,则在I 上f 为凸(凹)函数⇔()0f x ''>(()0f x ''<),x I ∈. 二、 曲线的拐点定义及判定1 定义2 设曲线y =f(x)在点(00,()x f x )处有穿过曲线的切线,且在切点近旁,曲线在切线的两侧分别是严格凸或严格凹的,这时称(00,()x f x )为曲线y =f(x)的拐点.注:拐点是严格凸与严格凹的分界点2定理6.15(拐点必要条件) 若f 在0x 二阶可导,则(00,()x f x )为曲线y =f(x)的拐点的必要条件是0()0f x ''=.综上知:(00,()x f x )的拐点,则要么(1)0()0f x ''=;要么(2)f 在0x 点不可导.3定理6.16 设f 在点0x 可导,在某邻域0()U x 内二阶可导,若在0()U x +和0()U x -上()f x ''的符号相反,则(00,()x f x )为曲线y =f(x)的拐点.;注:(00,()x f x )是曲线y=f (x)的一个拐点,但y =f(x)在点0x的导数不一定存在,如y =在x =0的情形.三、应用举例(1)利用上述等价命题验证函数的凹凸性,确定凹凸区间.例1 讨论函数()arctan f x x =的凸(凹)性及拐点.(2)证明不等式例2:(Jensen 不等式)若f 为],[b a 上凸函数,则对任意),,2,1(0],,[n i b a x i i =>∈λ11=∑=n i i λ,有)()(11ini i i n i i x f x f ∑∑==≤λλ 例3 证明均值不等式:,,,21+∈∀R a a a n 有na a a a a a a a a nn n n n +++≤≤+++ 212121111 作业:P153 1(2)(4),2,3,4,5。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
拐点的判定条件
拐点,就是指某一特定的时间点,该时间点可以标志一个特殊的变化,一般是在该时间点前的变化趋势和后的变化趋势相反,所以也可称为变化点。
拐点的出现受多方因素的影响,如政策因素、经济因素、市场因素、技术因素等。
科学判定拐点,需要遵循几个关键条件:
第一,多个变量间存在着统计学上的显著性差异,换言之,就是拐点出现的时刻,受影响的变量比较明显和众多。
第二,变量的改变有一定的可持续性。
比如,处于拐点之后的变量出现明显的、可持续的变化,而拐点之前的变量则没有明显的变化,反映出了非常明显的变化模式。
第三,变量变化的情况与相关因素有着直接的关联。
变量变化绝不是毫无联系和原因的,一定会存在一些有影响变量变化的因素,这些因素可以是政策因素、经济因素、市场因素、技术因素等。
第四,以上三项条件,都必须符合统计分析的特定要求,即控制统计偏差、消除外部干扰等。
以上就是拐点的判定条件,在实践中,需要充分综合考虑这些条件,识别变化的趋势,正确判断拐点的位置,以有效的抓住转折点的机会,实现变革。
许多时候,拐点的出现表明了一个时期的结束,也预示着新的变革时代的到来,例如1978年中国改革开放政策,从经济社会发展层面来看已经形成了一个重要的拐点。
这一拐点说明,中国从一个封闭
式社会过渡到了一个开放的市场经济,这对整个国家的发展将产生深远的影响。
在中国公司的业务中,也经常会出现拐点的情况,比如某家公司在开发一款新型产品,经过了一段时间的投入,但是至今仍未取得成功,此时就可以判定出一个拐点,表明该公司需要重新调整战略,以获得成功。
以上只是拐点判定条件的一些概括,在实际应用中,还需要更多的具体因素,比如针对不同变量的趋势、预测结果的分析等。
拐点的判定,不仅关乎依据的正确与否,也包括这些依据的合理性,只有建立在客观数据分析的基础上,才能准确判断出拐点的位置,为变革的实现指明正确的方向。
