电子课件张平平
合集下载
人教A版必修2高中高一PPT课件-2.2.2 平面与平面平行的判定

(D)α内的任何一条直线都与β平行.
2.如图:三棱锥P-ABC, D,E,F分别是棱PA,PB,PC
的中点, 求证:平面DEF∥平面ABC.
P
D
F
思路点拨:PD PE PF PA PB PC
A
E
C
B
3.如图正方体ABCD-A1B1C1D1中,E、F、G、H分别是棱A1D1, A1B1,B1C1,C1D1的中点.
2.2.2 平面与平面平行的判定
1.通过观察实物及模型,得出两平面平行的判定定理; 2.理解并掌握两平面平行的判定定理及其应用;(重点、难 点) 3.培养观察能力和空间想象能力; 4.了解空间与平面互相转换的数学思想.
平面与平面有哪几种位置关系?
如何判定平面和平面平行? 由两个平面平行的定义可得: 1.如果两个平面平行,那么在其中一个平面内的所有直线 一定都和另一个平面平行; 2.反过来,如果一个平面内的所有直线都和另一个平面平行, 那么这两个平面平行.
不可. 2.要证明平面与平面平行,只要在这个平面内找出两条相
交直线与已知平面平行,把证明面面问题转化为证明线面
问题即可.
ba
பைடு நூலகம்
P
1.平面和平面平行的条件可以是( D ) (A)α内有无穷多条直线都与已知平面平行. (B)直线a∥α,a∥β,且直线a不在α内,也不在β内.
(C)直线 a ,直线 b ,且a∥β,b∥α
符号语言:
a ,b
aI bP
/
/
a / /,b / /
ba
P
定理中必需的三个条件
a,b ① 在平面 内,即 ② a,b 相交,即 a I b P, ③ 平行,即 a / /,b / / .
2.如图:三棱锥P-ABC, D,E,F分别是棱PA,PB,PC
的中点, 求证:平面DEF∥平面ABC.
P
D
F
思路点拨:PD PE PF PA PB PC
A
E
C
B
3.如图正方体ABCD-A1B1C1D1中,E、F、G、H分别是棱A1D1, A1B1,B1C1,C1D1的中点.
2.2.2 平面与平面平行的判定
1.通过观察实物及模型,得出两平面平行的判定定理; 2.理解并掌握两平面平行的判定定理及其应用;(重点、难 点) 3.培养观察能力和空间想象能力; 4.了解空间与平面互相转换的数学思想.
平面与平面有哪几种位置关系?
如何判定平面和平面平行? 由两个平面平行的定义可得: 1.如果两个平面平行,那么在其中一个平面内的所有直线 一定都和另一个平面平行; 2.反过来,如果一个平面内的所有直线都和另一个平面平行, 那么这两个平面平行.
不可. 2.要证明平面与平面平行,只要在这个平面内找出两条相
交直线与已知平面平行,把证明面面问题转化为证明线面
问题即可.
ba
பைடு நூலகம்
P
1.平面和平面平行的条件可以是( D ) (A)α内有无穷多条直线都与已知平面平行. (B)直线a∥α,a∥β,且直线a不在α内,也不在β内.
(C)直线 a ,直线 b ,且a∥β,b∥α
符号语言:
a ,b
aI bP
/
/
a / /,b / /
ba
P
定理中必需的三个条件
a,b ① 在平面 内,即 ② a,b 相交,即 a I b P, ③ 平行,即 a / /,b / / .
直线与平面平行的判定公开课ppt课件
AD
AE AF
上的点,若 EB ,FD则EF与平面BCD的位置关系是
_E_F_/_/_平_面__B_C_D____.
利用平行线定理 证线线平行.
A F
E D
B
C
2.如图,四棱锥A-DBCE中,O为底面
正方形DBCE对角线的交点,F为AE的
中点. 求证: AB//平面DCF.
分析: 连结OF.
A F
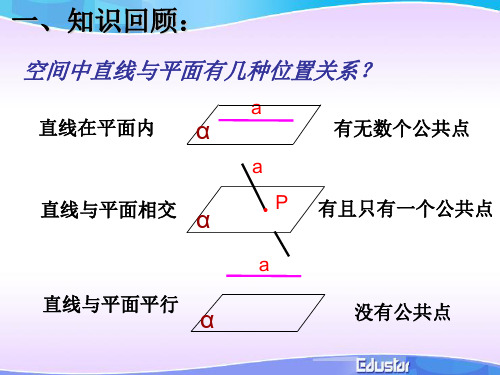
一、知识回顾:
空间中直线与平面有几种位置关系?
a
直线在平面内 α
有无数个公共点
直线与平面相交 α
a
.P 有且只有一个公共点
a 直线与平面平行
α
没有公共点
二、引入新课
怎样判定直线与平面平行呢?
a
三、实例感受
在门扇的旋转过程中: 直线AB在门框所在的平面外 直线CD在门框所在的平面内 直线AB与CD始终是平行的
因为E,F分别是AB,
E
F D
C
B
AD 的中点,所以EF//BD
因为 EF 平面BCD, BD 平面BCD
由直线与平面平行的判断定理得:
EF//平面BCD.
小结:在平面内找(作)一条直线与平面外的直线平行时可以通过 三角形的中位线、梯形的中位线、平行线的性质等来完成。
变式练习
1. 如图,在空间四边形ABCD中,E、F 分别为AB、
AD的中点.
∴EH∥BD且EH= 1 BD
同理GF
2
∥BD且GF=
1 2
BD
EH ∥GF且EH=GF
H E
D
B
G
∴E、F、G、H四点共面。
F C
(2) AC ∥平面EFGH
《两个平面平行》课件

平面平行的性质 定理:如果两个 平面平行,则它 们之间的直线也 是平行的。
03
平面平行的判定条件
判定条件一:若两平面内分别有两条相交直线,则两平面平行
• 定义:若两平面内分别有两条相交直线,则称这两平面为相交直线。 • 性质:若两平面为相交直线,则它们之间的距离为常数。 • 判定条件:若两平面内分别有两条相交直线,则这两平面平行。 • 证明:假设两平面分别为α和β,且它们内分别有两条相交直线a和b。由于a和b相交,它们确定一个平面γ。由于α和
• 应用:这个判定条件在几何学中有着广泛的应用,特别是在解决与平面几何相关的问题时。 以上内容仅供参考,具 体内容可以根据您的需求进行调整优化。
• 以上内容仅供参考,具体内容可以根据您的需求进行调整优化。
判定条件三:若两平面分别与第三个平面交于两条相交直线,则 两平面平行
定义:若两平面 分别与第三个平 面交于两条相交 直线,则称两平 面平行。
β都与γ相交,根据平面的性质,α和β必然平行。 注:这个判定条件是平面平行的基本判定条件之一,它在几何学 中有着广泛的应用。
• 注:这个判定条件是平面平行的基本判定条件之一,它在几何学中有着广泛的应用。
判定条件二:若两平面分别与第三个平面交于两条平行直线,则 两平面平行
• 定义:若两平面分别与第三个平面交于两条平行直线,则称两平面平行。
性质证明:根据平面几何的基本性质,两平面平行意味着它们之间 的距离保持不变,因此它们不会相交,也就没有公共点。
性质应用:在几何学中,这一性质被广泛应用于证明和推导定理。
性质的意义:这一性质是平面几何中的基本概念之一,对于理解平 面几何的性质和定理具有重要意义。
性质二:若两平面平行,则它们没有公共直线
北师大版必修第二册第六章立体几何初步平面和平面平行证明技法课件共28张PPT

因为 ⊥ , ⊥
B1B,所以 ⊥ 平面1 1 。
因为 1 ⊂ 平面1 1 ,,所以 ⊥ 1 。
又因为 1 ⊥ 1 ,所以 1 ⊥ 1 1 。
因为 1 ⊂ 平面1 1 ,所以 1 ⊥ 1 。
同理可得, 1 ⊥ 1 。
又 1 ∩ 1 = ,所以 1 ⊥平面 1 1 。同理可得, 1 ⊥平面 1 。
点评
特点:体现了垂直与平行的辨证关系
如果第一种方法是【内化】,此方法属
【外化】
缺点:证明线面垂直也是比较费事的,而
且是证明两次,好在用【同理】
方法三
平行同一平面
α
β
γ
平行于同一
个平面的两
又 ∩ = ,所以平面 //平面。
点评
1.面面平行的传递性,与线线平行的传递性相似
2.其实,如果能用这种方法,也能用第一种方法,
毕竟,已经有了两组线线平行
环节四
向量法
α
β
法向量平行
环节五
学以致用
1.如图,在正方体 − 1 1 1 1 中,求证:
个平面平行
侧3 如图3,在四棱锥SABCD中,P,Q,R分别是棱
SA,SB,SC的中点,M,N,O分
别在棱SA,SC,SD上,且
=
��
=
//平面MON。
=
1
,求证:平面PQR
2
证明:因为P,Q,R分别是棱SA,SB,SC的中点,所以 //, //。
又PQ⊄平面ABCD,AB⊂平面ABCD,由直线与平面平行的判定定理得 //
线线平行、线面平行和面面平行的证明可以相互
判定定理
B1B,所以 ⊥ 平面1 1 。
因为 1 ⊂ 平面1 1 ,,所以 ⊥ 1 。
又因为 1 ⊥ 1 ,所以 1 ⊥ 1 1 。
因为 1 ⊂ 平面1 1 ,所以 1 ⊥ 1 。
同理可得, 1 ⊥ 1 。
又 1 ∩ 1 = ,所以 1 ⊥平面 1 1 。同理可得, 1 ⊥平面 1 。
点评
特点:体现了垂直与平行的辨证关系
如果第一种方法是【内化】,此方法属
【外化】
缺点:证明线面垂直也是比较费事的,而
且是证明两次,好在用【同理】
方法三
平行同一平面
α
β
γ
平行于同一
个平面的两
又 ∩ = ,所以平面 //平面。
点评
1.面面平行的传递性,与线线平行的传递性相似
2.其实,如果能用这种方法,也能用第一种方法,
毕竟,已经有了两组线线平行
环节四
向量法
α
β
法向量平行
环节五
学以致用
1.如图,在正方体 − 1 1 1 1 中,求证:
个平面平行
侧3 如图3,在四棱锥SABCD中,P,Q,R分别是棱
SA,SB,SC的中点,M,N,O分
别在棱SA,SC,SD上,且
=
��
=
//平面MON。
=
1
,求证:平面PQR
2
证明:因为P,Q,R分别是棱SA,SB,SC的中点,所以 //, //。
又PQ⊄平面ABCD,AB⊂平面ABCD,由直线与平面平行的判定定理得 //
线线平行、线面平行和面面平行的证明可以相互
判定定理
8.5.3 平面与平面平行课件ppt

∴PM∥AB1.
又AB1∥C1D,∴PM∥C1D.
又PM⊄平面C1BD,C1D⊂平面C1BD,
∴PM∥平面C1BD.
同理MN∥平面C1BD.
又PM∩MN=M,
∴平面PMN∥平面C1BD.
探究二
面面平行性质定理的应用
例2如图,已知平面α∥平面β,点P是平面α,β外的一点(不在α与β之间),直线
PB,PD分别与α,β相交于点A,B和C,D.
D.平面α内有无数个点到平面β的距离相等且不为0,那么这两个平面平行
或相交
答案 CD
解析 如图①,在平面α内作α,β交线的无数条平行线,可知A,B错误;
对C,由题意可知AB∥β,BC∥β,AB∩BC=B,由面面平行的判定定理可知
α∥β,C正确;
对D,参考选项C的解析,假设α内有一个点位于点A处,而其余点均位于直线
所以PQ∥平面CBE.
(方法二)如图②,连接AC,则Q∈AC,且Q是AC的中点.
因为P是AE的中点,所以PQ∥EC.
因为PQ⊄平面CBE,EC⊂平面CBE,
所以PQ∥平面CBE.
方法点睛 (1)线线、线面、面面间的平行关系的判定和性质,常常是通过
线线关系、线面关系、面面关系的相互转化来表达的,因此在证明有关问
4
3
15
∴ = ,∴5 = ,∴CD= 4 ,
15 27
∴PD=PC+CD=3+ 4 = 4 .
反思感悟 证明线线平行的方法
(1)定义法:在同一个平面内没有公共点的两条直线平行.
(2)平行线的传递性:平行于同一条直线的两条直线平行.
∥
(3)线面平行的性质定理: ⊂
⇒a∥b,应用时题目条件中需有线面平行.
又AB1∥C1D,∴PM∥C1D.
又PM⊄平面C1BD,C1D⊂平面C1BD,
∴PM∥平面C1BD.
同理MN∥平面C1BD.
又PM∩MN=M,
∴平面PMN∥平面C1BD.
探究二
面面平行性质定理的应用
例2如图,已知平面α∥平面β,点P是平面α,β外的一点(不在α与β之间),直线
PB,PD分别与α,β相交于点A,B和C,D.
D.平面α内有无数个点到平面β的距离相等且不为0,那么这两个平面平行
或相交
答案 CD
解析 如图①,在平面α内作α,β交线的无数条平行线,可知A,B错误;
对C,由题意可知AB∥β,BC∥β,AB∩BC=B,由面面平行的判定定理可知
α∥β,C正确;
对D,参考选项C的解析,假设α内有一个点位于点A处,而其余点均位于直线
所以PQ∥平面CBE.
(方法二)如图②,连接AC,则Q∈AC,且Q是AC的中点.
因为P是AE的中点,所以PQ∥EC.
因为PQ⊄平面CBE,EC⊂平面CBE,
所以PQ∥平面CBE.
方法点睛 (1)线线、线面、面面间的平行关系的判定和性质,常常是通过
线线关系、线面关系、面面关系的相互转化来表达的,因此在证明有关问
4
3
15
∴ = ,∴5 = ,∴CD= 4 ,
15 27
∴PD=PC+CD=3+ 4 = 4 .
反思感悟 证明线线平行的方法
(1)定义法:在同一个平面内没有公共点的两条直线平行.
(2)平行线的传递性:平行于同一条直线的两条直线平行.
∥
(3)线面平行的性质定理: ⊂
⇒a∥b,应用时题目条件中需有线面平行.
八年级道德与法治上册(人民版)第七课第2课时《优势互补》公开课ppt课件

6 • 第二级
理解与尊重。
• 第三级
7
• 第四级
端庄与慎重。
• 第五级
8 正视与善后。在与异性交往中,如 果 已经“恋爱”,也要及时回头,妥善 处理,
继续做好朋友。
讲授新课
单击此处编辑母版标题样式
• 单击此处编辑母版文本样式
在•日第常二级生活中,如果你只和一位异性同
• 第三级
学交往•,第四关级 系很密切,花大量时间单独 • 第五级
随堂训练
单击此处编辑母版标题样式
2.有人说:“男女搭配,干活不累。” 这其中的奥秘是( D ) A•.单大•击第家此二可级处以编辑平母分版工文本作样式 B.大家• 第可三以级 边聊边干活 C.可以把• 第重四• 级第活五级推给对方干 D.两者之间可以优势互补,取长补短
•正第常•三第级的四级异性交往不仅有利于增进对异性 的了解,丰• 富第五级自身的情感体验,扩大社会交 往的范围,在正常的交往过程中实现性格差 异的互补,从而使集体更加团结,使个人的 优势得到展示,还可以消除两性之间的神秘
感,培养健康的性心理。
导入新课
单击此处编学辑习母目标版标题样式
•1.谈谈你对身边男生和女生交往现象的看法。 ••2单.•击说第此二说级处你编老辑师母和版文父本母样对式男生和女生交往现 象的看• 第法三级。 •3.认识• 男第四•女级第五同级 学之间交往的益处。 •4.正确对待闲言碎语,实现男女同学之间 正常健康的交往。
解、猜疑甚至干涉。
讲授新课
单击此处编辑母版标题样式
家•最 前长单•近那:击第就么•此是二第总级用处不三级编觉心是辑得了有母你。一版有你位文点说女本不,样生对式是对劲不你,是有学…点习…特也别没呀有,以我 小明:……• 第四级
高中数学课件两个平面平行的判定与性质ppt课件.优秀文档PPT

(2)重学生学习体验。 (1)判定两个平面平行的主要途径有那些.
定义
如果两个平面有公共点,它们就相交于一条过该公共点的直线,就称这两个平面相交.
提问:能否加上某些条件,从而由“线线平行”推出“面面平行”。
形式:讲述、提问、讨论
返回
过程分析 ——设计思路
问题: (1)若两条直线平行,则分别经过这两条直线的
(2)平面 BC CB内的直 BC 和 线 BC有什么关系?为
(3)若AA12,直A线 A和平A面 B所 C 成 NhomakorabeaC
3
的角6是 0,则两个平A行 B和 C平面A 2
B
ABC的距离是多少?
4C
1
A
B
课时小结
a
1.两个平面平行的性质
(1)一个结论 / /,a a/ /
面面平行
线面平行
(2)性质定理a/,/ba//b
②一条直线和两个平行平面相交,则此直线和两个平
面成等角;
③一条直线和两个平面成等角,则此两个平面平行;
④夹在两个平行平面间的两条线段长相等,那么这两
条线段平行.
A1 B2 C3 D4
巩固与拓展
3且.一不个为平零面,则上这不两同个的平三面点到另一个平面的距离( B相等)
A. 平行
B. 相交
C. 平行或重合
9.5.2两个平面平行的判定和性质
珲春一中 崔星
复习与引入
1.两个平面的位置关系
两个平面的位置关系只有两种 (1)两个平面平行——没有公共点 (2)两个平面相交——有一条公共直线.
l
符号表示 //
l
2.两个平面平行的判定
(1)判定定理:如果一
个平面内有两条相交直线
定义
如果两个平面有公共点,它们就相交于一条过该公共点的直线,就称这两个平面相交.
提问:能否加上某些条件,从而由“线线平行”推出“面面平行”。
形式:讲述、提问、讨论
返回
过程分析 ——设计思路
问题: (1)若两条直线平行,则分别经过这两条直线的
(2)平面 BC CB内的直 BC 和 线 BC有什么关系?为
(3)若AA12,直A线 A和平A面 B所 C 成 NhomakorabeaC
3
的角6是 0,则两个平A行 B和 C平面A 2
B
ABC的距离是多少?
4C
1
A
B
课时小结
a
1.两个平面平行的性质
(1)一个结论 / /,a a/ /
面面平行
线面平行
(2)性质定理a/,/ba//b
②一条直线和两个平行平面相交,则此直线和两个平
面成等角;
③一条直线和两个平面成等角,则此两个平面平行;
④夹在两个平行平面间的两条线段长相等,那么这两
条线段平行.
A1 B2 C3 D4
巩固与拓展
3且.一不个为平零面,则上这不两同个的平三面点到另一个平面的距离( B相等)
A. 平行
B. 相交
C. 平行或重合
9.5.2两个平面平行的判定和性质
珲春一中 崔星
复习与引入
1.两个平面的位置关系
两个平面的位置关系只有两种 (1)两个平面平行——没有公共点 (2)两个平面相交——有一条公共直线.
l
符号表示 //
l
2.两个平面平行的判定
(1)判定定理:如果一
个平面内有两条相交直线
部编六年级数学《解决问题》张一平PPT课件 一等奖新名师优质课获奖比赛公开北京

谢谢观赏!
一个盘子里至少有( 3)个苹果。
名师PPT课件
二、想一想: 1、19朵花插入4个花瓶里,总有一 个花瓶里至少有几朵花? 2、爸爸参加打靶比赛,打了5次, 成绩是43环。爸爸总有一次成绩至 少是9环,为什么?
延伸
名师PPT课件
名师PPT课件
请你任意写出4个自然数,在这 4个自然数中,总有两个数的差 是3的倍数。试一试,并结合抽 屉原理想一想,为什么?
名筷师子PP杯T课子件 列式为
数数
4 3 4÷3= 1……1
总有一个杯子里至少有 几根筷子?(至少数)
1+1=2
想一想:
名5根师P筷PT子课件放进4个杯子,不管怎么放,总
有一个杯子至少放进( 2)根筷子。
你
是
假设每个杯子里平均放
怎
( 1)根筷子,还剩下
样
( 1)根,。这1根不管
想
怎么放,总有一个杯子
筷子数比杯子数多1时,总有一个杯子里至少 有2根筷子。
独名立师P思PT考课件: 7只鸽子飞进5个鸽笼,总有
一个鸽笼里至.少.有(2)只鸽子。 7÷5=1… …2 1+1=2数
列式为
5 3 5÷3=1……2 9 4 9÷4=2……1 11 3 11÷3=3……2 13 5 13÷5=2……3
“比赛PPT课件,适合公开课赛课!”
义名务师教PP育T课课件程标准实验教科书六年级下册
武定县近城小学 张一平
名师PPT课件
抢凳子游戏规则: 1、老师喊“开始”时,3人围 着凳子快速绕圈;喊“坐下” 时,3人都必须坐在凳子上。 2、其他同学观察、思考,说 一说游戏中你发现了什么?
4名根师筷PP子T课放件进3个杯子里,不管怎么放,总 有一个杯子里至少有( 2)根筷子。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
义务教育课程标准试验教科书
教学设计
第三课时教学设计
新科题目第五课瑞雪图(课文)
标目学教
知识目标
要求学生能熟练地朗读课文。
能力目标
感情态度
和价值观
目标
让学生体会家乡冬天带来的乐趣
重点熟读课文及掌握课文。
难点掌握课文中的量词和词组。
教具教科书、课件
教学方式实验课演示课电教课多媒体课
汉语年级下册
一,学习课文内容
1.老师板书课题
第五课 瑞雪图
2•老师领读课文,学生跟读,并标出较难字的拼音
3•指名让学生朗读课文,老师纠正错误。
4再熟悉课文内容的基础上,边读边回答问题。
(1) 让学生朗读课文第一自然段。
a .提问:连日来,胶东半岛的天气怎么样?
指名回答,连日来,胶东半岛本来暖和得如同三月阳春的天气, 骤然变得冷起来了。
B.
掌握量词 一(个)下午
C.
掌握词组 ( 暖和)的天气 呼呼地(舌V )
(2) 全班朗读课文第二段 A .第二天早晨天晴日出时,山村冬天的景象是怎样的?
指名回答:山川,河流,树木,房屋,都被盖上了一层白茫茫的 厚雪,极目远
眺,万里江山变成了粉妆玉砌的世界。
b 量词一(层)白雪
一(个)世界 一(阵)风
一(道)彩虹
c ,词组 (粉妆玉砌 )的世界 (五光十色)的彩虹 (2)女生齐读课文第三段
计 设
程 过 学 教。
