风振及风振控制4-涡振ppt课件
合集下载
风振及风振控制-涡振PPT幻灯片课件
范围内和结构固有振动频率相等，即涡激共振的“锁定”现象。锁定现象增加了结构发
生涡振的机率，增强了三维结构上的涡激力的相关性。
• 涡激振动是一种限幅振动，对结构的质量和阻尼较为敏感，当结构质量和阻尼均较小时，
涡激共振振幅可能很大。
• 涡激振动常发生在较低风速下，出现频度较高，易使结构构件产生疲劳破坏、人感不适、
成桥后的振动实例
19
Li Jiawu ,The Faculty of Highway, Chang'an University
1.3.2金门桥主梁涡振
20
Li Jiawu ,The Faculty of Highway, Chang'an University
1.3.2金门桥主梁涡振
21
Li Jiawu ,The Faculty of Highway, Chang'an University
1.3.2金门桥主梁涡振
• 1938.2 强烈西风 行走困难 桥梁摇晃
•
未作观测 渐渐忘却（Tacoma垮桥）
• 1941.2.1 瞬时风速27m/s 持续3小5m 竖向频率 0.125Hz
•
最大弯曲位置 L/4 振幅 60cm
Li Jiawu ,The Faculty of Highway, Chang'an University
17
1.3.1 主梁涡振实例
成 桥 后 的 振 动 实 例
18
Li Jiawu ,The Faculty of Highway, Chang'an University
1.3.1 主梁涡振实例
1.2.1 涡激振动
•
风流经钝体结构时会在结构的两侧产生不对称的旋涡脱落，使结构表面受到周期性的
生涡振的机率，增强了三维结构上的涡激力的相关性。
• 涡激振动是一种限幅振动，对结构的质量和阻尼较为敏感，当结构质量和阻尼均较小时，
涡激共振振幅可能很大。
• 涡激振动常发生在较低风速下，出现频度较高，易使结构构件产生疲劳破坏、人感不适、
成桥后的振动实例
19
Li Jiawu ,The Faculty of Highway, Chang'an University
1.3.2金门桥主梁涡振
20
Li Jiawu ,The Faculty of Highway, Chang'an University
1.3.2金门桥主梁涡振
21
Li Jiawu ,The Faculty of Highway, Chang'an University
1.3.2金门桥主梁涡振
• 1938.2 强烈西风 行走困难 桥梁摇晃
•
未作观测 渐渐忘却（Tacoma垮桥）
• 1941.2.1 瞬时风速27m/s 持续3小5m 竖向频率 0.125Hz
•
最大弯曲位置 L/4 振幅 60cm
Li Jiawu ,The Faculty of Highway, Chang'an University
17
1.3.1 主梁涡振实例
成 桥 后 的 振 动 实 例
18
Li Jiawu ,The Faculty of Highway, Chang'an University
1.3.1 主梁涡振实例
1.2.1 涡激振动
•
风流经钝体结构时会在结构的两侧产生不对称的旋涡脱落，使结构表面受到周期性的
桥梁风振及其制振措施(PPT,17页)
主梁涡激振动 拉索风雨激振 桥塔涡激振动 主梁随机抖振
驰振 颤振
风振控制措施
颤振控制
驰振控制:
驰振和涡振控制
涡振控制: 提高结构阻尼比
施工时附加TMD、TLD或TLCD阻 尼器
风雨振控制
斜拉索表面制造成凹痕或螺旋线，可以减轻斜拉索风 雨振的程度。
加辅助索，预防拉索风雨振
机械减振措施
加阻尼器（如TMD，磁流变阻尼器）
TACOMA NARROWS BRIDGE
日本东京湾通道桥的涡激共振
主桥为10跨一联的钢箱梁连 续梁桥，最大跨度240m，宽 22.9m, 梁高6-11.5m。
在16-17m/s的风速作用下， 发生竖向涡激振动，跨中振幅 达50cD），涡激振动振幅只有 5 cm。
•驰振：细长结构因气流自激作用发生的纯弯曲大幅振动。如结 冰电线振动，塔柱、吊杆、拉索容易产生驰振形象。
•抖振：气流力受结构振动影响较小，气流力是一种强迫力，主 要是大气紊流导致结构强迫振动。
•涡振：大跨度桥梁在低风速下容易发生的一种 风致振动。
桥梁风振控制
绝对控制： 主梁风振失稳
尽量控制： 考虑控制：
•桥梁风振及其制振措施
Tacoma Narrows Bridge：位于美国华 盛顿州，1940年建成，三跨连续加劲 梁悬索桥，主跨853m，宽11.9m,加劲 梁为H型板梁，梁高2.45m。 建成4个月后，在18m/s的风速(8级)作 用下，发散振动持续70min。最后，吊 杆断裂，加劲梁坠落河中。 原因：颤振失稳。
斜拉索风雨振
日本名港西大桥（MeikoNishi）、洞庭湖大桥均实测到拉 索在风雨共存的条件下，发生风雨振。称为影响最大的一种桥 梁病害。
俄国伏尔加大桥“蛇形共振”
结构动力响应
f ha 0.221Hz
同济大学土木工程防灾国家重点实验室
4.1自振频率(续)
中国苏通大桥 (L=1088 m)
侧弯：f ps 0.098Hz,
竖弯：f 0.175Hz, hs 扭转：fts 0.532Hz
f pa 0.270Hz f ha 0.215Hz
A sin 0t B cos 0t 0 F (t )h(t )dt
0
1 s
2
1 exp sD t sin D t , D mD
0
同济大学土木工程防灾国家重点实验室
4.4
多自由度系统
振型方程：M j q j C j q j K j q j F j t 广义质量：M j 广义刚度：K j 广义阻尼：C j 广义荷载：F j
2
1 U 2 B CM ' 2CM p CM ' h nB / U 2
同济大学土木工程防灾国家重点实验室
5.2 自激力分量(续)
(2)非定常假设(Unsteady aerodynamics)
L f Lh h Lh h Lh h L L L Lp p Lp p L pp Lh h 2 Lh h Lh h L 2 L
V A
V Flutter or galloping
t 抖振 涡振
t 颤振或弛振
t
同济大学土木工程防灾国家重点实验室
4.结构动力特性
4.1 自振频率(Eigen or Natural Frequency)
法国Normandie Bridge (L=856 m)
结构风工程讲义--涡激振动
结构风工程学习资料---涡激振动当风流经细长钝体时，会产生流动分离以及周期性的旋涡脱落，从而在钝体上下表面出现正负压力的交替变化，这种压力的交替变化形成作用于钝体的涡激气动力，在一定条件下，会引起结构在横风向或扭转方向发生涡激共振。
涡振是一种带有强迫和自激双重性质的风致限幅振动，是结构中一种常见的风致振动。
涡振虽不具有很强的破坏性质，但由于其发生风速较低，长时间持续的振动将会造成结构损伤或疲劳破坏。
对于高层建筑，涡振引起的加速度会影响人的居住。
对于桥梁，涡振会影响行车的舒适性和安全性。
研究涡振主要关心三个问题：涡振风速、涡振频率和振幅。
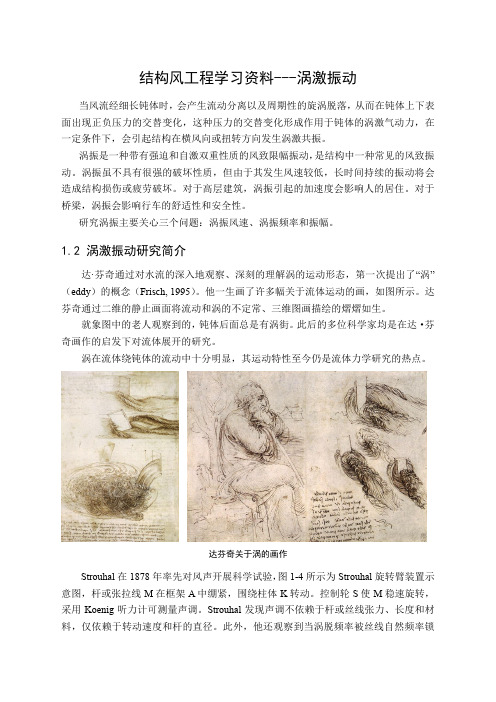
1.2 涡激振动研究简介达·芬奇通过对水流的深入地观察、深刻的理解涡的运动形态，第一次提出了“涡”（eddy）的概念（Frisch, 1995）。
他一生画了许多幅关于流体运动的画，如图所示。
达芬奇通过二维的静止画面将流动和涡的不定常、三维图画描绘的熠熠如生。
就象图中的老人观察到的，钝体后面总是有涡街。
此后的多位科学家均是在达·芬奇画作的启发下对流体展开的研究。
涡在流体绕钝体的流动中十分明显，其运动特性至今仍是流体力学研究的热点。
达芬奇关于涡的画作Strouhal在1878年率先对风声开展科学试验，图1-4所示为Strouhal旋转臂装置示意图，杆或张拉线M在框架A中绷紧，围绕柱体K转动。
控制轮S使M稳速旋转，采用Koenig听力计可测量声调。
Strouhal发现声调不依赖于杆或丝线张力、长度和材料，仅依赖于转动速度和杆的直径。
此外，他还观察到当涡脱频率被丝线自然频率锁定时丝线振动将会出现同步现象。
图1-4 Strouhal 旋转臂装置Strouhal 试验结果显示在一定条件下，气流流经固定的钝体时会脱落出交替的旋涡，其主频率f 可以由Strouhal 关系式得出：St UfD （1-1） 式中St 为Strouhal 数，D 代表物体的横风向尺寸，U 为浸没物体均匀流动的平均速度。
工程中的振动问题 ppt课件
PPT课件
16
海洋平台的减震（1983年）
渤海公司埕北油田A平台。 钻机开动时，平台振动强烈，生活区工人
很难入睡。 强烈振动有可能影响平台的寿命。 要求分析原因，采取有效的减震措施。
PPT课件
17
海洋平台的结构示意
钻机转速有三档，现用 一档。
三档转速为： n=90，120，150r/min
PPT课件
3
矿山通风机叶片开裂的治理（1990年）
平顶山矿 2K58-30通风机。 沈阳风机厂生产。 1988年11月至1989年10月，14支叶片开裂，
故被煤炭部冻结销售。 要求分析开裂原因，提出根治的措施。
PPT课件
4
2K58-30通风机的结构示意
转速 600r/min。
11 19
中导叶数 z2 =19, 机器转速为
n=10Hz。
扰动频率为nz1和 nz2。
0 50 100 150 200 250 300 Hz
扰动频率带为绿色区，不会激起叶片 共振。
改进工艺，减小叶片制造质量和频率
分散度。
PPT课件
10
风机的减震和隔震（1996年）
北京燕山石化一厂聚苯一烯车间，屋顶 上装有三台通风机F-730、731、732。
平台高度为 20多米，面 积有如半个足球场。
PPT课件
18
海洋平台的减震分析
初步观察：
走廊作水平转动，平台四角作 切向运动，故平台作扭转振动。
有限元计算：
第一阶扭振固有频率1.12Hz
实测：
固有频率1.1Hz。 扭转扰动频率：1.5Hz
结论： 平台为处于扭转共振中。
PPT课件
风振及控制6-颤振
当结构发生振动时，由于周围的绕流受结构变位的干扰而发生变化，导致 作用在结构上的空气力也随时间发生变化。这种作用力由于是伴随结构振动产生 的，称为自激气动力，它是非定常气动力的主要形式。
（1）Theodorson平板空气力公式
1935年，Th. Theodorson首先从 理论上研究了薄平版的非定常气动 力。他根据流体力学势流理论求得 了作用于振动平板上的非定常气动 力的解析表达式。对于图示二维理 想平板，在均匀水平流场中作微小 振动时所受到的非定常空气升力和 力矩可表达为：
2.2作用于桥梁的空气力
2.2.1．定常气动力
当气流以恒定不变的速度及方向绕过固定不动的物体时，就形成了 一定常的（即不随时间变化的）流场，空气对物体表面的动压力的合力 就是空气的作用力，也是定常的。对于二维流动，空气的定常作用力可 表达为静力三分力：
阻力
FH
1 2
V
2
HLC
H
升力 力矩
FV
时的折算速度即为临界值Kc，此时相应的颤振临界风速为
无量纲的Kc值称vc为r ThBKefoc dorson值（Th)，于是：
vc Th1Bf
2.5抗风设计中颤振稳定性的检验
1. 颤振稳定性检验准则：
Vcr [Vcr ]
式中颤振检验风速:
[Vcr ] K f Vd
K为安全系数，取１.２； f为考虑风速脉动影响及水平相关特性的无量纲修正系数； Vd为设计基准风速；
3
A1*表示竖向运动对力矩的贡献，A2*，A3*表示扭转运动对力矩的贡献。
典型断面颤振导数曲线
典型断面颤振导数曲线
2.3桥梁颤振计算理论的发展
1948年Bleich 第一次用Theodorson 的平板空气公式来解决悬索桥的颤振分析。 他认为在悬索桥中常用的桁架加劲梁的上承桥面接近于一块平板，此时悬索桥的 二维颤振微分方程可以写成：
（1）Theodorson平板空气力公式
1935年，Th. Theodorson首先从 理论上研究了薄平版的非定常气动 力。他根据流体力学势流理论求得 了作用于振动平板上的非定常气动 力的解析表达式。对于图示二维理 想平板，在均匀水平流场中作微小 振动时所受到的非定常空气升力和 力矩可表达为：
2.2作用于桥梁的空气力
2.2.1．定常气动力
当气流以恒定不变的速度及方向绕过固定不动的物体时，就形成了 一定常的（即不随时间变化的）流场，空气对物体表面的动压力的合力 就是空气的作用力，也是定常的。对于二维流动，空气的定常作用力可 表达为静力三分力：
阻力
FH
1 2
V
2
HLC
H
升力 力矩
FV
时的折算速度即为临界值Kc，此时相应的颤振临界风速为
无量纲的Kc值称vc为r ThBKefoc dorson值（Th)，于是：
vc Th1Bf
2.5抗风设计中颤振稳定性的检验
1. 颤振稳定性检验准则：
Vcr [Vcr ]
式中颤振检验风速:
[Vcr ] K f Vd
K为安全系数，取１.２； f为考虑风速脉动影响及水平相关特性的无量纲修正系数； Vd为设计基准风速；
3
A1*表示竖向运动对力矩的贡献，A2*，A3*表示扭转运动对力矩的贡献。
典型断面颤振导数曲线
典型断面颤振导数曲线
2.3桥梁颤振计算理论的发展
1948年Bleich 第一次用Theodorson 的平板空气公式来解决悬索桥的颤振分析。 他认为在悬索桥中常用的桁架加劲梁的上承桥面接近于一块平板，此时悬索桥的 二维颤振微分方程可以写成：
风力发电基础课件
回转平面与叶片截面
弦长的夹角
运动旋转方向
u R 2Rn
dL气流升力
相对
速度
dL
1 2
Cl w2dS
dD
1 2
Cd
w 2dS
dF气流w产生的气动力
驱动功率dPw= dT
风输入的总气动功率:P=vΣFa 旋转轴得到的功率:Pu=Tω
风轮效率η=Pu/P
叶片的几何参数
3. 旋转叶片的气动力(叶素分析)
v v1 v2 2
，
贝兹理
最大理想功率为：Pmax
8 27
Sv13
论的极 限值
风力机的理论最大效率：max
Pmax E
(8 / 27)Sv13
1 2
Sv13
16 27
0.593
风力发电机从自然风中所能索取的能量是有限的，其 功率损失部分为留在尾流中的旋转动能。
风力发电机基础理论
3.风力机的主要特性系数
对于有限长的叶片，风轮叶片下游存在着尾迹涡，它形成两 个主要的涡区：一个在轮毂附近，一个在叶尖。有限叶片数由 于较大的涡流影响将造成一定的能量损失，使风力机效率有所 下降。
1) 中心涡，集中在转轴上； 2) 每个叶片的边界涡； 3) 每个叶片尖部形成的螺旋涡。
涡流理论
叶片静止时，据赫姆霍兹定理，叶片附着涡和后缘尾涡 组成马蹄涡系。简化后，将叶片分成无限多沿展向宽度很小 的微段。
叶片的几何参数
2.升力和阻力的变化曲线
0.8
Cl •升力系数与阻力系数是随攻角变化的
0.6
0.4
失速点
0.2
Cd
i
i -30o -20o -10o 0o 10o 20o
-0.2 Cl min
弦长的夹角
运动旋转方向
u R 2Rn
dL气流升力
相对
速度
dL
1 2
Cl w2dS
dD
1 2
Cd
w 2dS
dF气流w产生的气动力
驱动功率dPw= dT
风输入的总气动功率:P=vΣFa 旋转轴得到的功率:Pu=Tω
风轮效率η=Pu/P
叶片的几何参数
3. 旋转叶片的气动力(叶素分析)
v v1 v2 2
，
贝兹理
最大理想功率为：Pmax
8 27
Sv13
论的极 限值
风力机的理论最大效率：max
Pmax E
(8 / 27)Sv13
1 2
Sv13
16 27
0.593
风力发电机从自然风中所能索取的能量是有限的，其 功率损失部分为留在尾流中的旋转动能。
风力发电机基础理论
3.风力机的主要特性系数
对于有限长的叶片，风轮叶片下游存在着尾迹涡，它形成两 个主要的涡区：一个在轮毂附近，一个在叶尖。有限叶片数由 于较大的涡流影响将造成一定的能量损失，使风力机效率有所 下降。
1) 中心涡，集中在转轴上； 2) 每个叶片的边界涡； 3) 每个叶片尖部形成的螺旋涡。
涡流理论
叶片静止时，据赫姆霍兹定理，叶片附着涡和后缘尾涡 组成马蹄涡系。简化后，将叶片分成无限多沿展向宽度很小 的微段。
叶片的几何参数
2.升力和阻力的变化曲线
0.8
Cl •升力系数与阻力系数是随攻角变化的
0.6
0.4
失速点
0.2
Cd
i
i -30o -20o -10o 0o 10o 20o
-0.2 Cl min
2019年动力气象学第四章.ppt
0
位涡守恒
4．大尺度大气运动 且是均质大气－－热力作用？
k
Const
d dt
(
1
a
ln
)
0
d dt
(
a
z
ln
)
0
5．位涡守恒的应用 气柱爬越高原：
d ln 2 0
dt
d ln 1 0
dt
ln ln 1 ln 2 d ( a ) 0
df
v
(
w
w )
dy
x y
(p x
y
p y
x
)
F
Z
v u
x y
① ( f ) V
f V
散度项
＝v u V 105 s 1 f 104 s 1
x y L
2）物质环线是闭合的，“环流” 表示流体随闭合环线运动的趋势， 描述了涡旋的强度。 是积分量。
3．“涡度”的定义
V
速度的旋度
1）刚体的运动形式有：平动，转动； 流体的运动形式有：平动，转动和形变， 涡度表示的是流体涡旋运动的强度。
2）“涡度”是欧拉观点下的，是微
分量。
3）可证：
2
（涡度＝2倍角速度）。
例：地球在垂直向的牵连涡度为：
f 2sin
（二）大尺度大气涡旋运动 1．大涡尺度度大主气要运是动在是垂准直水方平向运上动，，即所：以
k
2．绝对涡度 ＝相对涡度＋牵连涡度：
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
风振及风振控制4-涡振
16
1.3 涡激振特点
• 是一种较低风速区发生的有限振幅振动 • 只在某一风速区域内发生 • 最大振幅对阻尼有很大的依赖性 • 断面形状的微小变化对响应很敏感 • 涡激振动可以激起弯曲振动，也可以激 17
1.3.1 主梁涡振实例
成 桥 后 的 振 动 实 例
18
1.3.1 主梁涡振实例
• 冯·卡门1881年5月11日出生于匈牙利布达佩斯 • 16岁的冯·卡门在1898年11月进了布达佩斯皇家工学院 • 1906年去德国哥廷根（Göttingen）大学求学，师从普朗特（Ludwig
Prandtl 1875-1953）教授。 • 第一次世界大战期间，冯·卡门应召为奥匈帝国服务4年。战后曾任匈
4.45 5
• 3 近垂直桥轴SW75 ° 20.03 114.3
• 4 近桥轴
31.15 30
• 否定“斜风导致实际开孔率下降导致振动”的假定
• 1950.6.6 西风 风速20.03~24.92m/s 振幅 114.3cm
• 短时反对称一次扭转振动出现
23
1.3.2金门桥主梁涡振
• 1951.12.1 • 西风 风速 30.08m/s 振幅 335cm • 南希·肯特小姐的故事 • 下午和朋友乘车过桥，经过南塔后遭遇强风 • 左打右转方向，汽车倒退不前，桥上已看不见其他车
0
14.5
14.6
14.7
14.8
14.9
15
15.1
15.2
15.3
15.4
15.5
Sec. 122 0.6
0.4
0.2
0
-0.2
-0.4
-0.6
14.5
14.6
14.7
14.8
14.9
15
15.1
15.2
15.3
15.4
15.5
•
最大弯曲位置 L/4 振幅 60cm
•
无扭转振动记录
• 原因 Tacoma桥 板梁 桁架化 抗风措施
•
金门桥 桁架开孔率>25﹪
•
斜风导致实际开孔率下降？
22
1.3.2金门桥主梁涡振
• 桥轴方向 序号 风向 风速m/s 振幅cm
• NW10° 1 近桥轴SW12 ° 22.25 5
• 2 近垂直桥轴W
二、风致振动
1.涡激振动 2.颤振 3.驰振 4.抖振
风振及风振控制4-涡振
1
1.涡激振动
1.1 卡门涡旋 1.2 涡激振动 1.3 涡振特性 1.4 涡振估算 1.5涡振的控制措施
风振及风振控制4-涡振
2
1.1 卡门涡街
1.1.1 卡门涡街
卡门涡街是流体力学中重要的现象，在一定条件下的定常来流绕过某些物体
辆 • 想起了Tacoma桥，当车开过北塔到达北岸 • 看到了等候过桥的长长的车队 • 金门桥开通14年来，首次封闭交通2小时50分
24
1.3.3 大海带桥涡振
Drag coefficient Critical wind speed
Vortex induced response
25
0.6 0.4 0.2
作用，使旋涡脱落频率在一定风速范围内和结构固有振动
风振及风振控制4-涡振
7
1.2.2 圆柱涡激振动特点（与Re有关）
• 亚临界范围（3.0×102<Re<3.0×105)，旋涡 以一个明确的频率周期性地脱落
• 在临界范围（3.0×105≤Re<3.5×106)，旋涡 被紊流所掩盖，涡脱杂乱无章
• 在超临界范围（3.5×106<Re)，涡重新建立， 涡脱重新出现周期性
成桥后的振动实例
19
1.3.2金门桥主梁涡振
20
1.3.2金门桥主梁涡振
21
1.3.2金门桥主梁涡振
• 1938.2 强烈西风 行走困难 桥梁摇晃
•
未瞬时风速27m/s 持续3小时
•
水平攻角 45°风攻角 0°
•
横向变位1.5m 竖向频率 0.125Hz
• 不同雷诺数情况下风振及的风振绕控制4流-涡振 形态不同，因而 8
1.2.2 圆柱涡激振动
风振及风振控制4-涡振
9
1.2.3 Strouhal数及“锁定” 现象
St
fd U
10
• 当被绕流的物体不是固定不动的，而是 一个振动体系时，周期性涡激力将引起 体系的涡激共振，结构的振动对旋涡的 脱落产生一种反馈作用，使旋涡脱落频 率在一定的风速范围内被“俘获”，即 在该风速范围内物体的固有频率控制了 涡脱的频率，从而产生了一种“锁定” 现象。
时，物体两侧会周期性地脱落出旋转方向相反、排列规则的双列线涡，经过
非线性作用后，形成卡门涡街
风振及风振控制4-涡振
3
1.1.1 卡门涡街
• 卡门涡街视频 • 桥梁断面
风振及风振控制4-涡振
4
1.1.2 冯 ·卡门
• 冯·卡门（Theodore von Kármán １８８１—１９６３）是美藉匈牙利 裔力学家，近代力学的奠基人之一，是我国著名科学家钱学森、钱伟 长、郭永怀，以及美藉华人科学家林家翘在美国加州理工学院时的导 师。
牙利苏维埃共和国教育部大学副部长。
• 后他又回到德国亚琛工学院任教，担任亚琛空气动力学研究所所长。
• 1929年底起定居美国,任加州理工学院古根海姆空气动力学实验室主任。 • 后来建立了美国火箭技术中心——喷气推进实验室
风振及风振控制4-涡振
5
1.1.2 冯 ·卡门
• 作为德国亚琛工学院空气动力学研究所和美国加州理工学院古根海姆 空气动力学实验室的领导，带领了两代科学家和工程师进入了科学技 术的前沿领域，为航空和航天工程奠定了坚实的科学基础。冯·卡门培 育出了大批杰出的人才,他的学生遍及五大洲，被誉称为“卡门科班”。
• 在锁定区内，涡脱频率不再服从Strouhal 11
1）Strouhal数的影响因素
截面形状 雷诺数(对于
钝体断面,影 响比较小)
12
2）圆柱的Strouhal数
St = 0.2
13
14
15
1.2.4 易发生涡激振动构件
1）主梁（西堠门） 2）桥塔（钢桥塔） 3）吊杆（系杆拱吊杆，H型）
风振及风振控制4-涡振
6
1.2 涡激振动
1.2.1 涡激振动
•
风流经钝体结构时会在结构的两侧产生不对称的旋涡
脱落，使结构表面受到周期性的正负压力，在一定风速下
结构所受合力的频率与结构的自振频率一致，此时结构发
生涡激共振。
• 涡激振动是一种简谐振动，其振动形式通常表现为横
风向振动或扭转振动。
• 结构振幅较大时，结构的运动对气体的绕流形态产生反馈